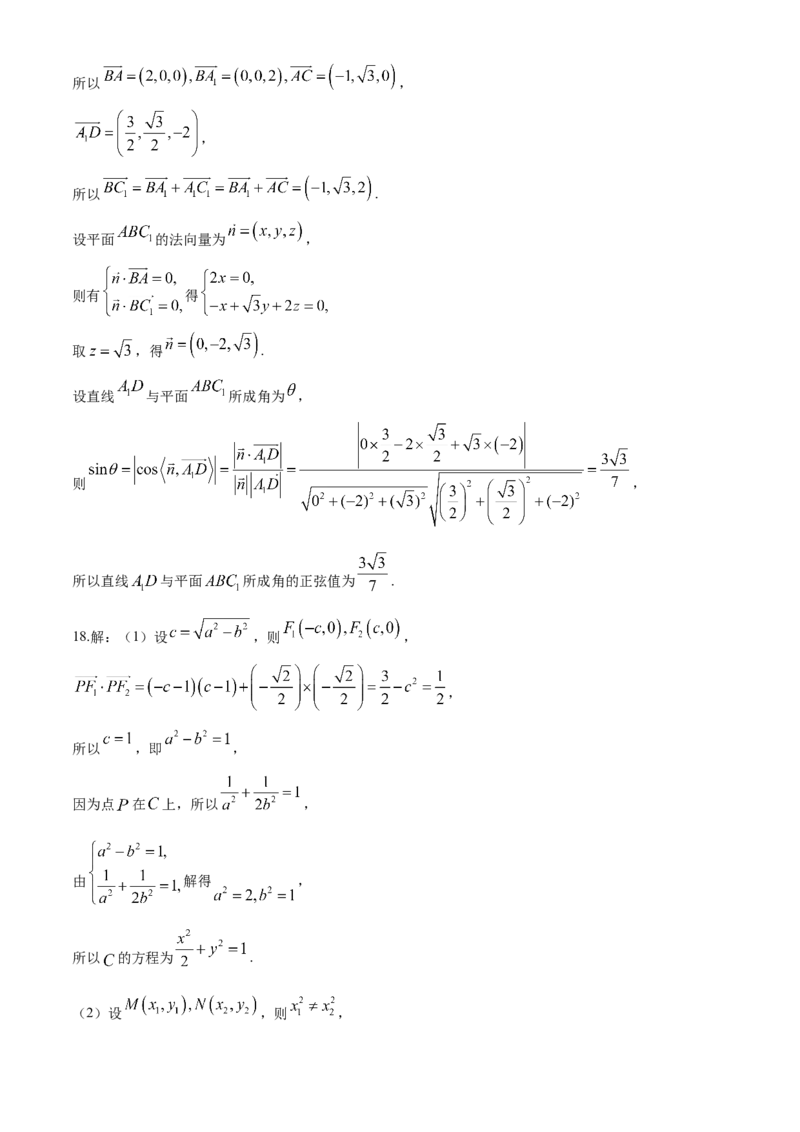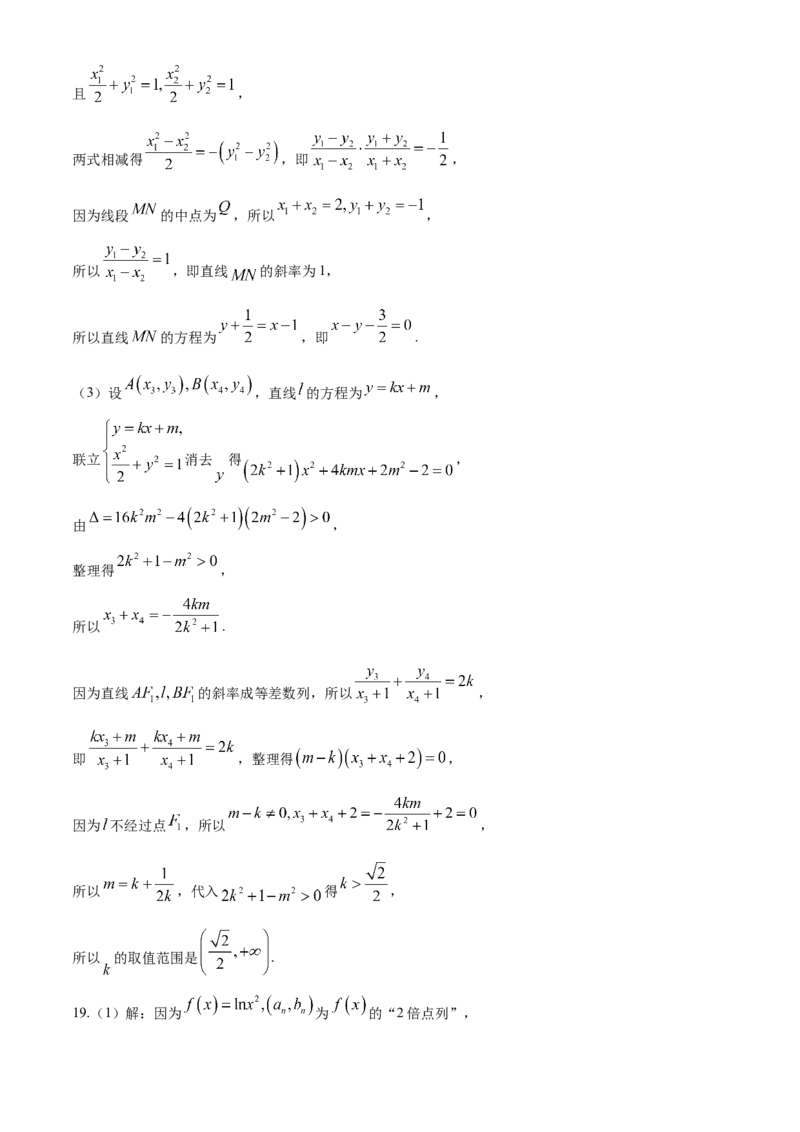文档内容
2024-2025 学年高三 12 月质量检测卷
数学
考生注意:
1.本试卷分选择题和非选择题两部分.满分150分,考试时间120分钟.
2.答题前,考生务必用直径0.5毫米黑色墨水签字笔将密封线内项目填写清楚.
3.考生作答时,请将答案答在答题卡上.选择题每小题选出答案后,用 铅笔把答题卡上对
应题目的答案标号涂黑;非选择题请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答题
区域内作答,超出答题区域书写的答案无效,在试题卷、草稿纸上作答无效.
4.本卷命题范围:高考范围.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
1.若 ,则 ( )
A. B. C. D.
2.已知集合 ,则 ( )
A. B.
D.
3. 的展开式中常数项为( )
A. B.30 C. D.15
4. ( )
A. B. C. D.
5.已知 ,动点 满足 ,动点 满足 ,则 的最
小值为( )
A. B.2 C. D.
学科网(北京)股份有限公司6.设函数 在 上单调递增,则实数 的取值范围( )
A. B. C. D.
7.已知抛物线 的焦点为 是 上不同的两点, 为坐标原点, ,则
的最小值为( )
A. B. C. D.9
8.同底的两个正三棱锥 与 的所有顶点都在球 的表面上,若 2,则二面角
的余弦值为( )
A. B. C. D.
二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目
要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.已知 是两条不同的直线 是两个不同的平面, ,则( )
A. 不平行是 不平行的充分条件
B. 不相交是 不相交的必要条件
C. 垂直且相交是 垂直的充分条件
D. 平行或相交是 异面的必要条件
10.已知函数 的定义域 ,对任意的 ,恒有
,则下列结论正确的是( )
A.
B. 是奇函数
C.若 ,则
学科网(北京)股份有限公司D.若 ,则
11.某科技企业通过一家代工厂为其加工某种零部件,加工后的零部件先由智能检测系统进行检测,智能检
测系统能检测出不合格零部件,但会把 的合格零部件判定为不合格,所以智能检测系统检测出的不合
格零部件需要进行人工第二次检测,人工检测可以准确检测出合格与不合格的零部件,通过统计需要人工
进行第二次检测的零部件中,零部件的合格率为 ,则( )
A.该零部件的合格率为
B.从该代工厂加工的零部件中任取100个,则取到的合格品个数的均值为96
C.从该代工厂加工的零部件中先后两次各取一个,若至少有1个为合格品,则第1次取到合格品的概率为
D.从需要进行人工第二次检测的零部件中任取10件,取到5件或6件合格品的概率最大
三、填空题:本题共3小题,每小题5分,共15分.
12.若向量 满足 ,且 ,则 __________.
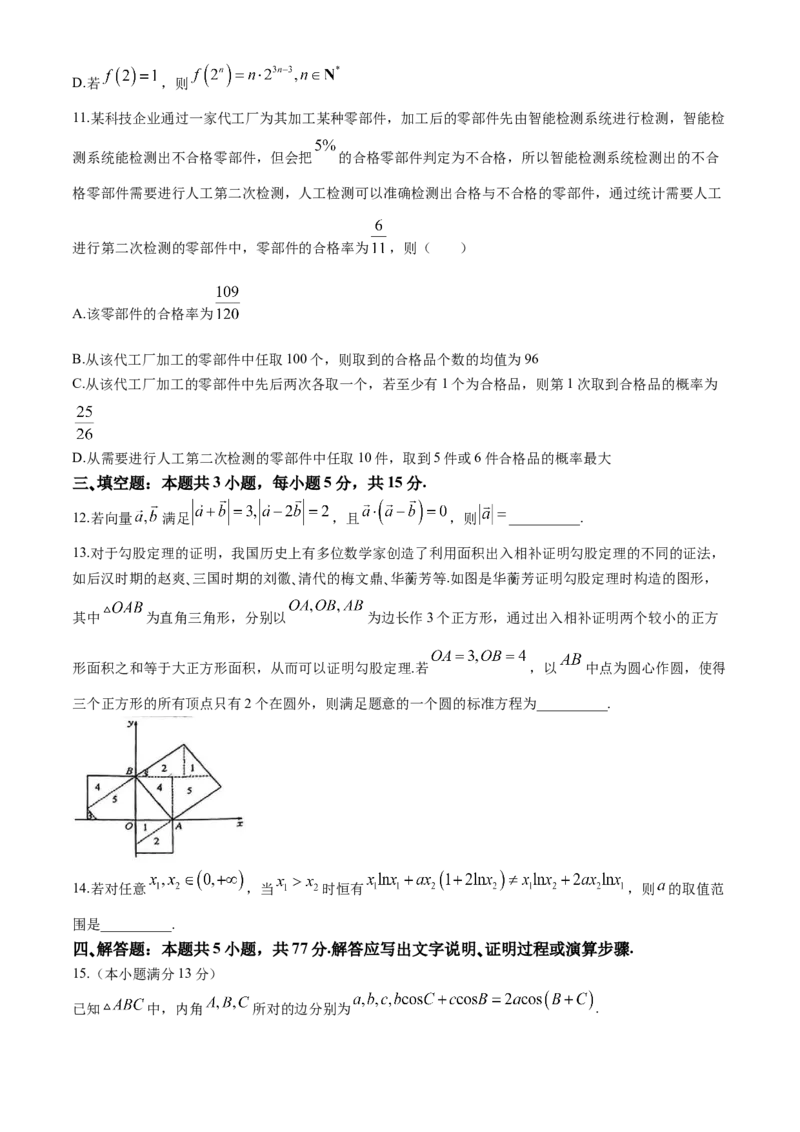
13.对于勾股定理的证明,我国历史上有多位数学家创造了利用面积出入相补证明勾股定理的不同的证法,
如后汉时期的赵爽、三国时期的刘徽、清代的梅文鼎、华蘅芳等.如图是华蘅芳证明勾股定理时构造的图形,
其中 为直角三角形,分别以 为边长作3个正方形,通过出入相补证明两个较小的正方
形面积之和等于大正方形面积,从而可以证明勾股定理.若 ,以 中点为圆心作圆,使得
三个正方形的所有顶点只有2个在圆外,则满足题意的一个圆的标准方程为__________.
14.若对任意 ,当 时恒有 ,则 的取值范
围是__________.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(本小题满分13分)
已知 中,内角 所对的边分别为 .
学科网(北京)股份有限公司(1)若 ,求 面积的最大值;
(2)若 ,求 .
16.(本小题满分15分)
近年来,因使用手机过久、工作压力大等因素导致不少人出现了睡眠问题.某媒体为了了解出现睡眠问题者
的年龄分布,调查了200名成年人的睡眠时间,得到如下列联表:
90后 非90后 合计
23:00前入 30 80
睡
23:00后入
睡
合计 100 200
(1)完成列联表,根据小概率值 的独立性检验,分析能否认为“23:00前入睡”与“是90后”
有关联?
(2)随着出现睡眠问题人群的增加,及社会对睡眠健康重视程度的加深,有助提高睡眠质量的产品受到
消费者推崇,记 年的年份代码 依次为1,2,3,4,5,下表为 年中国睡眠经
济市场规模及2024年中国睡眠经济市场规模(单位:千亿元)预测,
年份代码 1 2 3 4 5
市场规模 3.8 4.2 4.5 5.0 5.3
根据上表数据求 关于 的回归方程.
参考公式: ,其中 .回归方程 ,
其中
参考数据: .
17.(本小题满分15分)
如图,在体积为 的三棱柱 中,底面 是边长为2的正三角形, 、 为
的中点.
学科网(北京)股份有限公司(1)求证:平面 平面 ;
(2)求直线 与平面 所成角的正弦值.
18.(本小题满分17分)
已知椭圆 经过点 的左、右焦点分别为 ,且 . .
(1)求 的方程;
(2)若过点 的直线与 交于点 、 ,且线段 的中点恰好为 ,求直线 的方程;
(3)若斜率为 且不经过点 的直线 与 交于不同两点 ,直线 的斜率成等差数
列,求 的取值范围.
19.(本小题满分17分)
若 的定义域为 ,数列 满足 ,则称 为 的“ 倍点
列”.
(1)若 为 的“2倍点列”,求 的前 项和 ;
(2)若 为 的“1倍点列”且 ,求证: 为定值;
(3)若 ,判断是否存在 ,使得 为 的“ 倍点列”,并
证明你的结论.
学科网(北京)股份有限公司2024~2025 学年高三 12 月质量检测卷·数学
参考答案、提示及评分细则
1.A 因为 ,所以 ,则 .故选A.
2.D 因为 ,所
以 .故选D.
3.B 的展开式中常数项为 .故选B.
4.A 原式 .故
选A.
5.C 点的轨迹是双曲线 的右支,设 ,由 可得
学科网(北京)股份有限公司,整理得 点轨迹方程为 ,所以 .故选C.
6.C 因为函数 在 上单调递增,则需满足 解得 .故选C.
7.A 设 ,则 ,所以
,当且仅当
,即 时等号成立.故选A.
8.B 由题意可得 为球 的直径, ,因为 ,所以 ,
作 ,垂足为 ,则 为 外接圆半径,且 ,所以在正 中,
,取 中点 ,连接 ,则 就是二面角 的平面角.
,所以
.故选B.
9.BD 不平行, 有可能平行,故A错误;若 不相交,则 不相交,故B正确;若
学科网(北京)股份有限公司垂直相交, ,
可能不垂直,故C错误;若 异面,则 平行或相交,故D正确.故选BD.
10.ABD 中取 得 ,取 ,得
,故A正确;取 得 ,故B正确;由题意构造函数
,取 ,满足 ,此时 ,所以 ,
即 ,故C错误;取 ,得
,所以 ,又 ,所以
,故D正确.故选ABD.
11.BCD 设零部件的合格率为 ,由题意可得 ,解得 ,故A错误;从该
代工厂加工的零部件中任取100个,记取到的合格品个数为 ,则
,故B正确;从该代工厂加工的零部件中先后两次各取一个,
至少有1个为合格品的概率为 ,所以所求概率为 ,故C正确;从需要进行人
工第二次检测的零部件中任取10件,记取到 件合格品,则
,所以当
时, ,当 时, ,当 时, ,所以
学科网(北京)股份有限公司或 最大,故D正确.故选BCD.
12. 由 得 ;由 得 ;由
得 ,所以 .
13. (答案不唯一,形如 的方程都可
以) 的中点 ,点 到三个正方形顶点的距离最大为 ,其次为 ,所以该圆的一个
标准方程为 .
14. 由 得 ,即
,设 ,则 ,所以问题转化为 在 上没
有零点.当 0时, 没有零点,满足题意;当 时,由 得 ,设
,
则 ,因为 ,所以 在 上单调递增,在 上单调递减,因为
,所以 ,所以 .
综上, 的取值范围是 .
15.解:因为 ,所以 .
由正弦定理得 ,
学科网(北京)股份有限公司因为 ,且 ,
所以 .
(1)由 及余弦定理得 ,
所以 ,当且仅当 时取等号,
所以 的面积 ,
即 面积的最大值为 .
(2)由 及正弦定理得 ,
因为 ,所以 ,
所以 ,即 ,
所以 .
16.解:(1) 列联表如下:
90后 非90后 合计
前入睡 30 50 80
后入睡 70 50 120
合计 100 100 200
零假设 :“23:00前入睡”与“是90后”无关联,
因为 ,
根据小概率值 的独立性检验,我们推断 不成立,即认为“ 前入睡”与“是90后”有
关联,此推断犯错误的概率不超过0.01.
(2)由 的取值依次为 ,
学科网(北京)股份有限公司得 ,
所以 ,
,
所以 ,
所以 关于 的回归方程为 .
17.(1)证明:因为 是边长为2的正三角形,设点 到平面 的距离为 ,
则三棱柱 的体积 ,所以 ,
因为 ,所以 就是点 到平面 的距离,故 平面 .
因为 平面 ,所以 ,
因为 为 中点,所以 ,
因为 平面 ,所以 平面 ,
因为 平面 ,所以平面 平面 .
(2)解:以 为原点,直线 为 轴,在平面 内过点 与 垂直的直线为 轴,直线 为
轴建立空间直角坐标系,如图所示,
则 ,
学科网(北京)股份有限公司所以 ,
,
所以 .
设平面 的法向量为 ,
则有 得
取 ,得 .
设直线 与平面 所成角为 ,
则 ,
所以直线 与平面 所成角的正弦值为 .
18.解:(1)设 ,则 ,
,
所以 ,即 ,
因为点 在 上,所以 ,
由 解得 ,
所以 的方程为 .
(2)设 ,则 ,
学科网(北京)股份有限公司且 ,
两式相减得 ,即 ,
因为线段 的中点为 ,所以 ,
所以 ,即直线 的斜率为1,
所以直线 的方程为 ,即 .
(3)设 ,直线 的方程为 ,
联立 消去 得 ,
由 ,
整理得 ,
所以 .
因为直线 的斜率成等差数列,所以 ,
即 ,整理得 ,
因为 不经过点 ,所以 ,
所以 ,代入 得 ,
所以 的取值范围是 .
19.(1)解:因为 为 的“2倍点列”,
学科网(北京)股份有限公司所以 ,即 ,
所以
所以 ,
当 时,
,
综上,
(2)证明:因为 ,
所以 .
设 ,则 ,
所以 单调递增,且 ,
所以 在 上单调递减,在 上单调递增,
因为 为 的“1倍点列”,则 ,
不妨设 ,
,
所以 的图象关于直线 对称,当 时, 有2个不同实根,
所以 .
(3)解:因为 ,且 为 的“ 倍点列”,
可得 ,即 且 ,
学科网(北京)股份有限公司设 ,则 ,
在 上单调递增,且 ,
所以 时, 时, ,
所以 在 上单调递减,在 上单调递增,
因为 ,所以 且 时 ,
所以不存在 ,使得 ,
即不存在 ,使得 为 的“ 倍点列”.
学科网(北京)股份有限公司