文档内容
2023~2024 学年高三阶段性测试
数学
考生注意:
1.本试卷分选择题和非选择题两部分。满分150分,考试时间120分。
2.答题前,考生务必用直径0.5mm黑色墨水签字笔将密封线内项目填写清楚。
3.考生作答时,请将答案答在答题卡上。选择题每小题选出答案后,用 2B铅笔
把答题卡上对应题目的答案标号涂黑;非选择题请用直径 0.5mm黑色墨水签字
笔在答题卡上各题的答题区域内作答,超出答题区域书写的答案无效,在试题
卷、草稿纸上作答无效。
4.本卷命题范围:集合、常用逻辑用语、不等式、函数、导数、三角函数、数列。
一、选择题:本题共 8 小题,每小题 5 分,共 40 分。在每小题给出
的四个选项中,只有一项是符合题目要求的。
1. 若复数z满足 z(1+2i)=2−i (i为虚数单位),则 =( )
z
A. 1 B. −1 C. i D. −i
2.已知 ,B={x|log x≤1},若 ,则a的取值范围( )
a
A. [1,+∞) B. (1,+∞) C. (0,1) D. (0,1]
π ( π)
3.已知角α∈(0, ),且满足3√2sin α− =cosα,则sinα+2cosα =( )
2 4
25 25
A. −2 B. C. − D. 2
16 16
4. 荀子《劝学》中说:“不积跬步,无以至千里;不积小流,无以成江海.”所以说学习
是日积月累的过程,每天进步一点点,前进不止一小点.我们可以把(1+1%) 365看作是
每天的“进步”率都是 ,一年后是1.01365≈37.7834;而把(1−1%) 365看作是每天
“退步”率都是 ,一年后是0.99365≈0.0255.若李响同学和肖济同学基础相同,从现
在开始,李响同学每天“进步” ,而肖济同学每天“退步”1% ,经过230天后,李
学科网(北京)股份有限公司响同学的水平大约是肖济同学的( ). 参考数据:lg101≈2.0043,lg99≈1.9956)
A.50倍 B.70倍 C.90倍 D.100倍
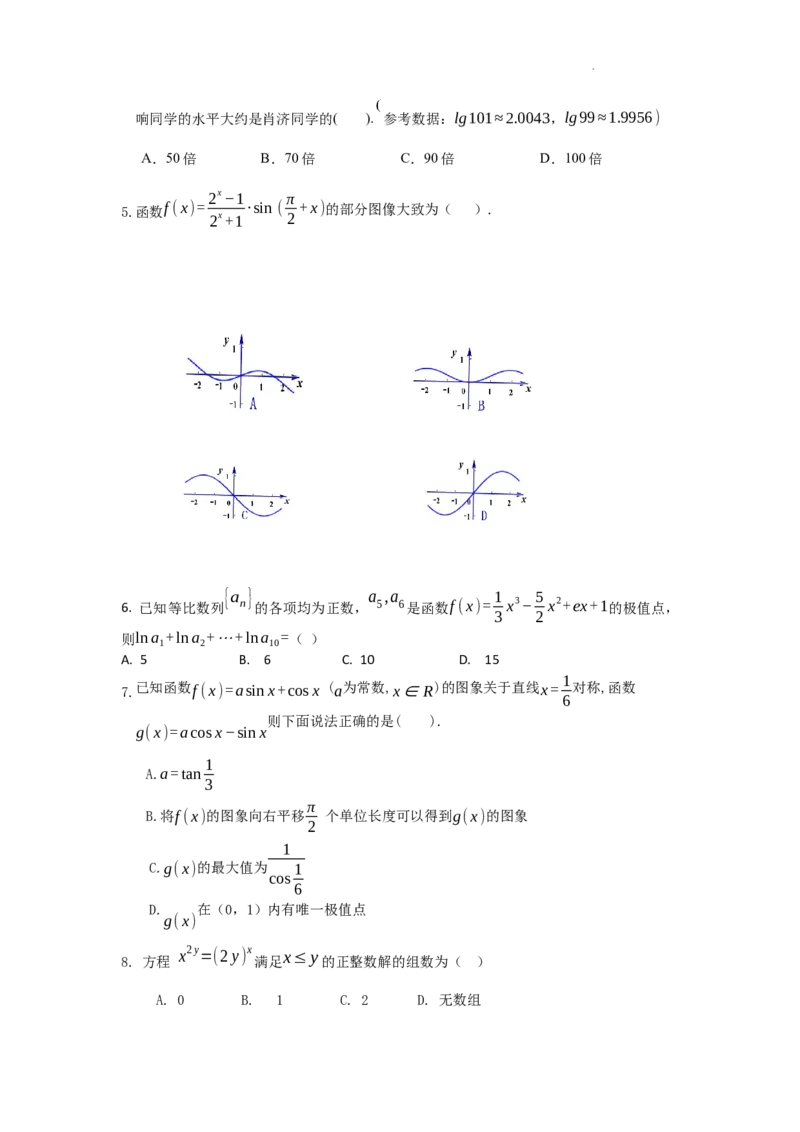
2x−1 π
5.函数 f(x)= ∙sin( +x)的部分图像大致为( ).
2x+1 2
{a } a ,a 1 5
6. 已知等比数列 n 的各项均为正数, 5 6是函数f(x)= x3− x2+ex+1的极值点,
3 2
则lna +lna +⋯+lna =( )
1 2 10
A. 5 B. 6 C. 10 D. 15
1
7.
已知函数f(x)=asinx+cosx (a为常数,x∈R)的图象关于直线x= 对称,函数
6
则下面说法正确的是( ).
g(x)=acosx−sinx
1
A.a=tan
3
π
B.将f(x)的图象向右平移 个单位长度可以得到g(x)的图象
2
1
C.g(x)的最大值为 1
cos
6
D. 在(0,1)内有唯一极值点
g(x)
x2y =(2y) x x≤y
8. 方程 满足 的正整数解的组数为( )
A. 0 B. 1 C. 2 D. 无数组
学科网(北京)股份有限公司二、选择题:本题共 4 小题,每小题 5 分,共 20 分。在每小题给出
的选项中,有多项符合题目要求。全部选对得 5分,部分相对的得 2
分,有选错的得0分。
9.下列命题正确的是( )
A. , 的否定为
∃x∈R x2+2x+1≤0 ∀x∈R,x2+2x+1>0
b+m b
B. a>b>0是 > 的充分不必要条件
a+m a
1 1
C.a> 是 <3的充分不必要条件
3 a
D. 且 是 的必要不充分条件
x≤1 y≤1 |x|+|y|≤2
.
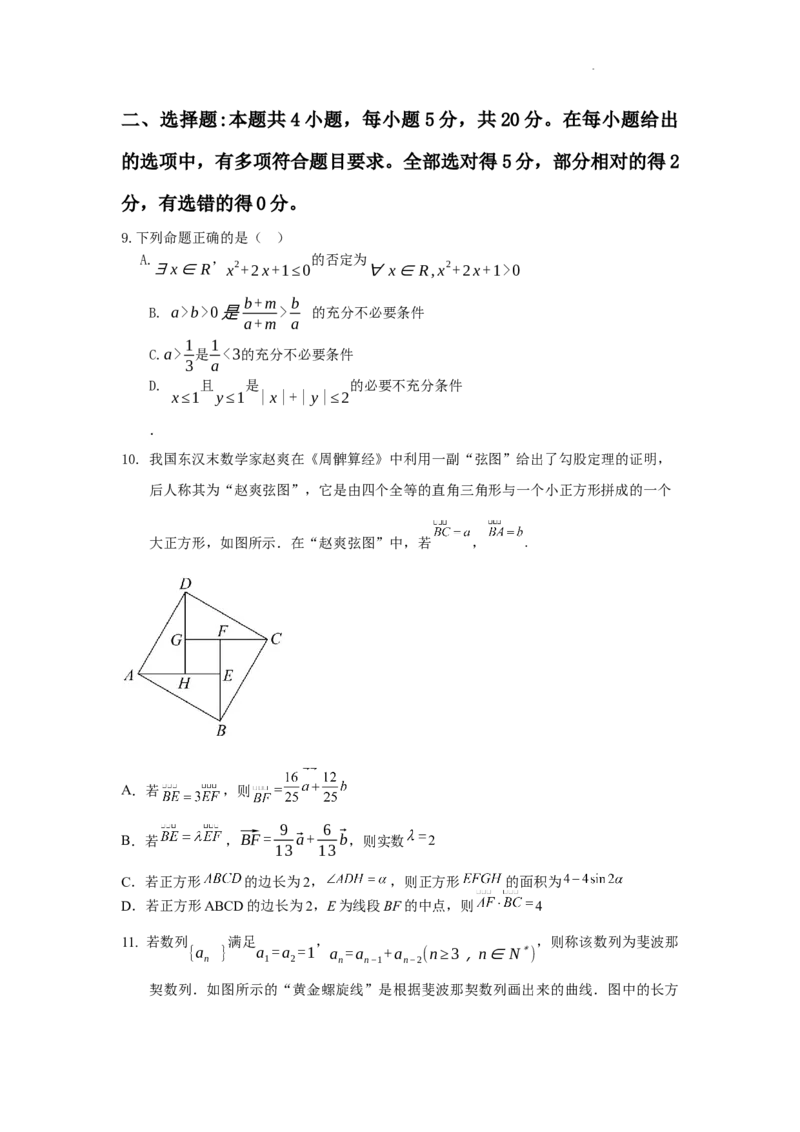
10. 我国东汉末数学家赵爽在《周髀算经》中利用一副“弦图”给出了勾股定理的证明,
后人称其为“赵爽弦图”,它是由四个全等的直角三角形与一个小正方形拼成的一个
大正方形,如图所示.在“赵爽弦图”中,若 , .
A.若 ,则 =
9 6
B.若 ,⃗BF= ⃗a+ ⃗b,则实数 2
13 13
C.若正方形 的边长为2, ,则正方形 的面积为
D.若正方形ABCD的边长为2,E为线段BF的中点,则 4
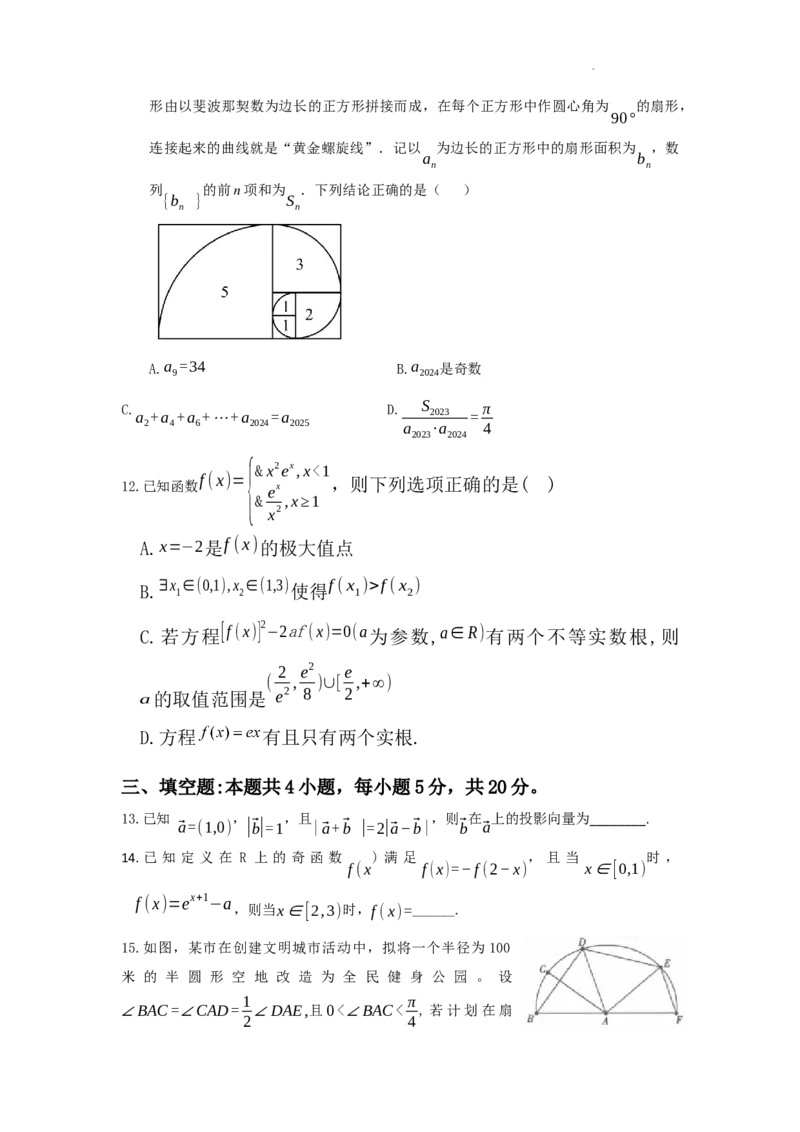
11. 若数列 满足 , ,则称该数列为斐波那
{a } a =a =1 a =a +a (n≥3,n∈N∗)
n 1 2 n n−1 n−2
契数列.如图所示的“黄金螺旋线”是根据斐波那契数列画出来的曲线.图中的长方
学科网(北京)股份有限公司形由以斐波那契数为边长的正方形拼接而成,在每个正方形中作圆心角为 的扇形,
90°
连接起来的曲线就是“黄金螺旋线”.记以 为边长的正方形中的扇形面积为 ,数
a b
n n
列 的前n项和为 .下列结论正确的是( )
{b } S
n n
A.a =34 B.a 是奇数
9 2024
C. D. S π
a +a +a +⋯+a =a 2023 =
2 4 6 2024 2025 a ∙a 4
2023 2024
{&x2ex,x<1
f(x)= ,则下列选项正确的是( )
12.已知函数 ex
& ,x≥1
x2
A.x=−2是f (x)的极大值点
B.∃x ∈(0,1),x ∈(1,3)使得 f (x )>f (x )
1 2 1 2
C.若方程[f(x)] 2 −2af(x)=0(a为参数,a∈R)有两个不等实数根,则
2 e2 e
( , )∪[ ,+∞)
a的取值范围是
e2 8 2
D.方程 有且只有两个实根.
三、填空题:本题共4小题,每小题5分,共20分。
13.已知 , ,且 ,则 在 上的投影向量为________.
⃗a=(1,0) |⃗b|=1 |⃗a+⃗b |=2|⃗a−⃗b| ⃗b ⃗a
14. 已 知 定 义 在 R 上 的 奇 函 数 ) 满 足 , 且 当 时 ,
f(x f (x)=−f(2−x) x∈[0,1)
f(x)=ex+1 −a
,则当x∈[2,3)时,f(x)=______.
15.如图,某市在创建文明城市活动中,拟将一个半径为100
米 的 半 圆 形 空 地 改 造 为 全 民 健 身 公 园 。 设
1 π
∠BAC=∠CAD= ∠DAE,且0<∠BAC< ,若计划在扇
2 4
学科网(北京)股份有限公司形ABC和四边形DAFE内安装健身器材,其余空地绿化,则运动健身区域占地面积的最大值
为_______平方米.
max{a,b}= {a }
16. 定 义 , 若 数 列 n 的 前 n项 和 为
s
n
=λn2 +(20+λ)n(λ∈R,n∈N¿),
数 列
{b
n
}
满 足 b =2,2n+1∙(b −b )=b b ,令
1 n+1 n n n+1
c =max{a ,b } c ≥c λ
n n n ,且 n 2恒成立,则实数 的取值范围是_______.
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17. (本小题满分10分)
π π
f(x)=2√3cos(2ωx− )−2sin2ωx(0<ω<1) f ( )=2
3 , 6
函数
f (x)
(1)求函数 的解析式;
1
f (x) 2 y=g(x)
(2)将 的图象纵坐标伸长到原来的2倍,横坐标缩短到原来的 倍,得到
[0,2π]
的图象,求方程 在 内的所有实数根之和.
18.(本小题满分12分)
已知数列 满足
(1).求数列 的通项公式;
(2).若_________,求数列 的前项和 .
请从① ② ③ 这三个条件中任选一个,补
充在上面的横线中,并完成解答.(注:如果选择多个条件分别解答,按第一个解答记分)
19.(本小题满分12分)
已知函数f (x)=ex−x2−1.
(1)求f (x)在x=1处的切线方程;
x0,
(2)若f (x)≤ax在 上有解,求实数a的取值范围.
20. (本小题满分12分)
a,b,c,
在△ABC中,角A,B,C的对边分别为
学科网(北京)股份有限公司1+cos2A sin2B
=
已知:
2cosA+sin2A 1+cos2B
π
B=
(1)若
6
,
b=3
,求△ABC的面积;
4sin2A+3sin2B+2
sin2C
(2)求 的最小值,并求出此时角C的大小.
21.(本小题满分12分)
党的二十大报告指出:必须坚持科技是第一生产力、人才是第一资源、创新是第一动力。
科技兴则民族兴,科技强则国家强。2023年9月,华为Mate60系列的发布再次引发了广
泛关注,它不仅展示了中国科技产业的不断进步和发展,更体现了中国人民自主创新、顽
强不屈的精神。某芯片企业原有400名技术人员,年人均投入 万元 ,现为加大对
研发工作的投入,该企业把原有技术人员分成技术人员和研发人员,其中技术人员 名,
调整后研发人员的年人均投入增加 ,技术人员的年人均投入调整为 万元.
(1)若要使调整后研发人员的年总投入不低于调整前400名技术人员的年总投入,求调整后
的研发人员的人数最少为多少人?
(2)为了激励研发人员的工作热情和保持技术人员的工作积极性,企业决定在投入方面要同
时满足以下三个条件:①技术人员不少于100人,不多于275人;②研发人员的年总投入
始终不低于技术人员的年总投入;③技术人员的年人均投入始终不减少.请问是否存在这
样的实数 ,满足以上两个条件,若存在,求出 的范围;若不存在,说明理由.
22. (本小题满分12分)
已知函数 f (x)=lnx−ax2+x
(1)求函数f(x)的单调区间;
4
(2)若方程f (x)=(1−x)lnx有两个不等的实数根x ,x ,且x >2x ,证明:√x2+x2> .
1 2 2 1 1 2 e
参考答案
2−i
z(1+2i)=2−i,z= =−i
1. C解: 1+2i ,∴z=i∴选C
学科网(北京)股份有限公司x
1 <0,x(x−1)<0
2. B解:由 <−1得:x−1 ∴01
,∴选B
4 π
tanα= α∈(0, )
3(sinα−cosα)=cosα 3 2
3. D解:由已知得 ,∴ ,∵
4 3
sinα= ,cosα= ,sinα+2cosα=2
5 5
∴ ∴选D
4. B解:设两人现在的水平为1,经过230天后,李响同学的水平大约是肖济同学的t倍.
1.01230 101 101
t= =( ) 230,lgt=lg( ) 230 =230(lg101−lg99)≈2,∴t≈100
0.99230 99 99
则
2x −1 1
f(x)= ⋅cosx f(1)= ⋅cos1>0
2x +1 f (x) 3
5. A解:由题可得: ,则 为奇函数。又由 ,
3
f (2)= ⋅cos2<0
5
,所以选A
f' (x)=x2 −5x+e∴a a =e ln(a a ⋯a )=lne5 =5∴
6. A解: 5 6 ,原式= 1 2 10 选A
1 1 1 1
x= f (0)=f ( ) 1=asin +cos
f (x) 6 3 3 3
7. C 解 析 关 于 对 称 , 则 , ,
:
1 1 1 1
∴asin =1−cos =2sin2 ∴a=tan
3 3 6 6 f (x) π/2
, A错, 向右平移 个单位长度,得
1 π π 1
y=tan ⋅sin(x− )+cos(x− )=−tan ⋅cosx+sinx≠g(x)
6 2 2 6
到 B 错 误 ,
√ 1 1
g(x) = tan2 +1=
max 6 1 1 1
cos g(x)=− sin(x− )
6 1 6
C 正 确 cos , 因 为
6
1 1 5
x∈(0,1),∴x− ∈(− , ) ,由图知g(x) 在 (0,1) 上没有极值点. D错.
6 6 6
学科网(北京)股份有限公司lnx ln(2y) lnx
= f(x)=
x 2y x
8.B 解 : 由 题 可 得 : , , 令 ,
1−lnx
f' (x)=
x2
,
f (x) (0,e) (e,+∞) f (x)>0
在 单调递增, 单调递减,当x>e时, 恒成立,又
f(1)=0
,
x≤y,f(x)=f(2y)∴x<2 y 且 x∈(1,e),2y∈(e,+∞) 又x,y为正整数,则 x=2 ,
ln2 ln4
f(2)= = =f(4)
2 4 2y=4,y=2 x=y=2
∴ ∴方程的解为 ∴选B
9.
AC解:∃x∈R,x2 +2x+1≤0
的否定为
∀x∈R,x2 +2x+1<0
,故A对;
1
1 2 b+m b <3
a=3,b=2,m=−1 < a>b>0 > ∴ a
当 时, 2 3 ,由 推不出 a+m a B错;由 化简得:
1 1
3− >0⇔a(3a−1)>0∴a<0 a> ∴
a 3 x=1.5,y=0.5
或 C正确;当 时,满足
|x|+|y|≤2但不满足x≤1且y≤1,∴D错。
10.ABC解:若 ⃗BE=3⃗EF 则 ⃗BF=⃗BC+⃗CF=⃗BC+ 3 (⃗BA−⃗BE)=⃗BC+ 3(⃗BA− 3 ⃗BF ) =
4 4 4
3 9 16 12 λ
⃗a+ ⃗b− ⃗BF∴⃗BF= ⃗a+ ⃗b∴A正确。因为⃗BE=λ⃗EF∴⃗BE= ⃗BF
4 16 25 25 λ+1
λ , λ λ λ2
∴⃗CF= ⃗CG ⃗BF=⃗BC+⃗CF=⃗a+ ⃗CG=⃗a+ ⃗b− ⃗BF
λ+1 λ+1 λ+1 (λ+1) 2
{ (λ+1) 2 9
= &
∴⃗BF= (λ+1) 2 ⃗a+ λ2+λ ⃗b∴ 2λ2+2λ+1 13 解得: λ=2 ∴B 正
2λ2+2λ+1 2λ2+2λ+1 λ2+λ 6
=
2λ2+2λ+1 13
确。
HG=2cosα−2sinα,∴s =4(1−sin2α)∴C对.
EFGH
4 3 16
⃗AF= ⃗a− ⃗b,∴⃗AF∙⃗BC= ∴D错。
5 5 5
11.ABD解:该数列为1,1,2,3,5,8,13,21,37,⋯所以a =37,A正确。
9
由斐波那契数列得每三个数中,前两个为奇数后一个为偶数,且 2024=
学科网(北京)股份有限公司3×674+2∴a 是奇数,B正确。由a =a −a ,得:a =a −a ,a =a −a ,⋯,
2024 n−1 n n−2 2 3 1 4 5 3
a =a −a , 累 加 得 : a +a +⋯+a =a −a ,∴C错 。 由
2024 2025 2023 2 4 2024 2025 1
,得:
a =a +a (n≥3) a 2+a 2+a 2+⋯+a 2=a ∙a +a 2+a 2+⋯+a 2
n n−1 n−2 1 2 3 2023 1 2 2 3 2023
=a (a +a )+a 2+⋯+a 2=a a +a 2+⋯+a 2=a (a +a )+⋯+a 2=a a +⋯+a 2=a a
2 1 2 3 2023 2 3 3 2023 3 2 3 2023 3 4 2023 2023 2024
所以 π π s π 对。
s = (a 2+a 2+a 2+⋯+a 2)= a a ∴ 2023 = ∴D
2023 4 1 2 3 2023 4 2023 2024 a a 4
2023 2024
12.AB解:当 时 ,则
∴ 在 单调递增, 单调递减, 单调递增∴
x=−2
是
f (x)
的极
大值点A正确。画出 的大致图象,可知B正确。方程 等
价于 或 由图知 有一个实数根 ,要使原方程有两个实
数根等价于 只有一解。由图可得: 或 故C错;由图可得
两函数图象有三个交点故D错。故选AB
3
( ,0)
13.
5
解 : 由 题 可 得 :
|⃗a+⃗b| 2 =4|⃗a−⃗b| 2
, 设
⟨ ⃗a,⃗b⟩=θ
,
3 3
2+2cosθ=4(2−2cosθ),∴cosθ= ( ,0)
5 ⃗b ⃗a 5
,则 在 上投影向量为
14.ex−1−e 解:f (x)+f (2−x)=0,∴f(x)关于(1,0)对称,又f(x)为奇函数,∴T=2,
当 时 , , 当
f (0)=e−a=0∴a=e , x∈[0,1) f (x)=ex−1−e
x∈[2,3),f (x)=f (x−2)=ex−1−e
π
2500π ∠BAC=θ(0<θ< )
+5000√3 4
3 .解:设 ,
15.
则
[θ 1 1 ] π
s(θ)=10000 + sin2θ+ sin(π−4θ) =5000(θ+sin2θ+sin4θ),(0<θ< )
2 2 2 4
s' (θ)=5000(1+2cos2θ+4cos4θ)=5000(8cos22θ+2cos2θ−3)
1 π
s' (θ)>0,cos2θ> ∴0<θ<
=5000(2cos2θ−1)(4cos2θ+3) 2 6
,令 ,
学科网(北京)股份有限公司π π π
(0, ) ( , ) (π) 2500π
s(θ) 6 6 4 s(θ) =s = +5000√3
故 在 单调递增, 上单调递减,则 max 6 3
16. −8≤λ≤−3 解:由数列 {a n } 的前n项和为 s n =λn2 +(20+λ)n(λ∈R,n∈N¿),
当
n≥2
时,可得:
a
n
=s
n
−s
n−1
=2λn+20
,又由当
n=1
时
a
1
=s
1
=20+2λ
,符合
{a } a =2λn+20 {b }
上 式 , 所 以 数 列 n 的 通 项 公 式 为 n , 由 数 列 n 满 足
b =2,2n+1 (b −b )=b b ,
1 n+1 n n n+1 可得:
1 1 1
− =
b
n
b
n+1
2n+1
,当
n≥2
时,由累加法得:
b
n
=2n
,当
n=1
时,符合上式,所以数列
{b } b =2n c =max{a ,b } c ≥c
n 的通项公式为 n ,由 n n n ,且 n 2恒成立,则需满足 ,
所以−8≤λ≤−3
π π
f(x)=√3cos2ωx+sin2ωx=2sin(2ωx+ ) f ( )=2
3 6 得:
17.解: ,由
πω π π 1 1
+ = +2kπ ω= +6k(k∈z) ω=
3 3 2 ∴ 2 ,又0<ω<1∴ 2
π
f(x)=2sin(x+ )
∴ 3
⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯
6分
π [0,2π] [0,2π]
(2)g(x)=4sin(2x+ ),T=π,g(x)在 内恰有两个周期∴ 在
3
x 0
,∴
cosC<0
,∴
2
⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯
3分
π 2π
B= C=
(1) ∵
6
,∴
3
,∴△ABC为等腰三角形,∴
a=b=3
1 2π 9√3
S = absin =
ΔABC 2 3 4
⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯
5分
π π 3π
C= +B B=C− ,A=π−B−C= −2C
2 2 2
(2)∵ ,∴ ,代入化简得:
4cos22C+3cos2C+2 4(1−2sin2C) 2 +3(1−sin2C)+2 16sin4C−19sin2C+9
= =
sin2C sin2C sin2C
9 √ 9 9
=16sin2C+ −19≥2 16sin2C⋅ −19=5 16sin2C=
sin2C sin2C sin2C
当且仅当 即
√3 2π 2π
sinC= C= C=
2 3 3 ⋯⋯⋯⋯
, 时等号成立,该式的最小值是5,此时 12分
21.(1)依题意可得调整后研发人员的年人均投入为 万元,
则 ,整理得 ,
解得 ,故25≤400−x≤400,
所以要使这 名研发人员的年总投入不低于调整前400名技术人员的年总投入,调
整后的研发人员的人数最少为25人.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ (6分)
(2)由条件②研发人员的年总投入始终不低于技术人员的年总投入,得
学科网(北京)股份有限公司,
上式两边同除以 得 ,整理得 ;
由条件③技术人员年人均投入不减少,得 ,解得 ;
由条件①得100≤x≤275,x∈N∗,
假设存在这样的实数 , 使得技术人员在已知范围内调整后,满足以上三个条件,
即 (100≤x≤275,x∈N∗)恒成立,
因为 ,
当且仅当 ,即 时等号成立, 所以 ,
又因为 ,当 时, 取得最大值 ,所以 ,
所以 ,即 ,
即存在这样的 满足条件,其范围为 .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ (12分)
1 −2ax2+x+1
(1)f'(x)= −2ax+1= (x>0)
x x
22.
①当a≤0时, 恒成立, 在(0,+∞)单调递增,
a>0 f'(x)=0
② 时, , 解得 ,由韦达定理可得
所以 有一正一负两个实数根。令 解得
在 单调递增, 在 上单调递减
a≤0 f(x) (0,+∞) a>0 f(x)
综上所述:当 时, 在 单调递增, 时 在
学科网(北京)股份有限公司单调递增,在 单调递减.
⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯
(4分)
(2)由f (x)=(1−x)lnx得:lnx−ax2+x=lnx−xlnx, 即xlnx−ax2+x=0,即
lnx−ax+1=0∴
设 ,因为 ,所以 ,且 ,
代入②可得: ,所以 ③,
又由①可得 ,所以 ,
代入③可得: ,所以 ,
故 ,
从而 ,
设 ,则 ,
设 ,则 ,所以 在 上单调递增,
又 ,所以 恒成立,故 ,从而 在 上单调递
增,
因为 ,所以 ,从而 ,
故 ,所以 . ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯(12
分)
学科网(北京)股份有限公司