文档内容
高三数学
第Ⅰ卷(选择题 共60分)
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
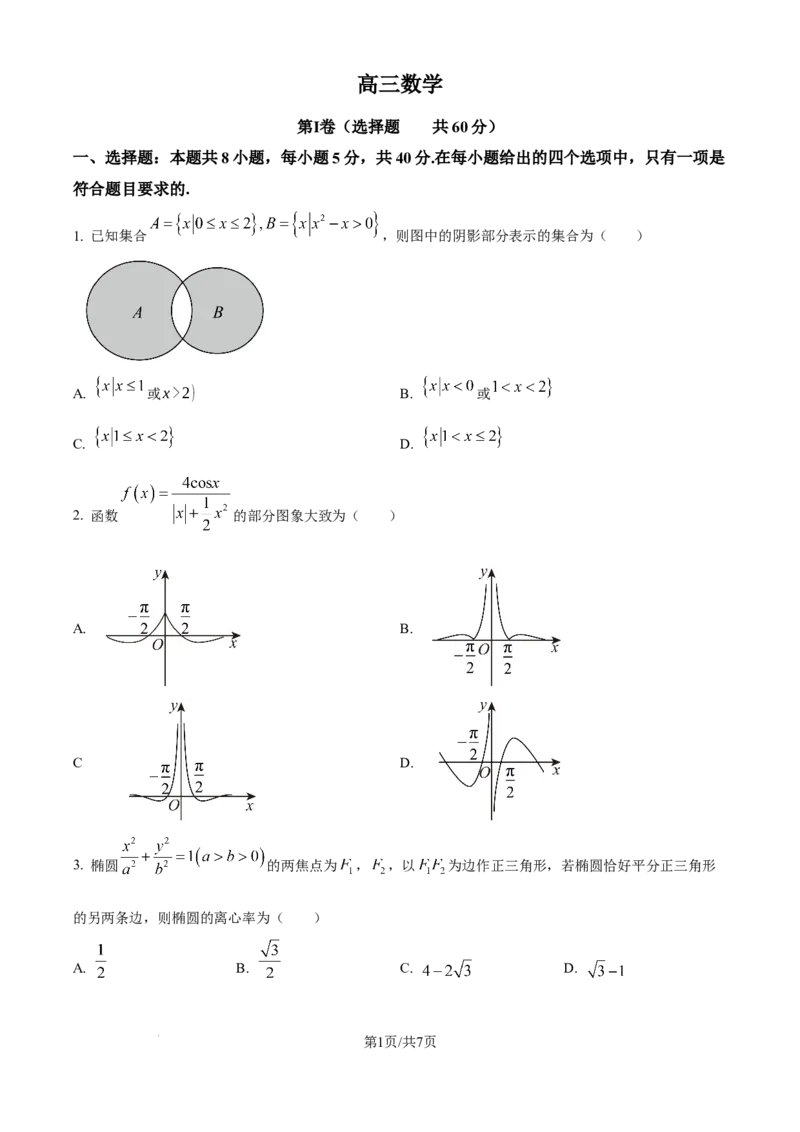
1. 已知集合 ,则图中的阴影部分表示的集合为( )
A. 或x>2) B. 或
C. D.
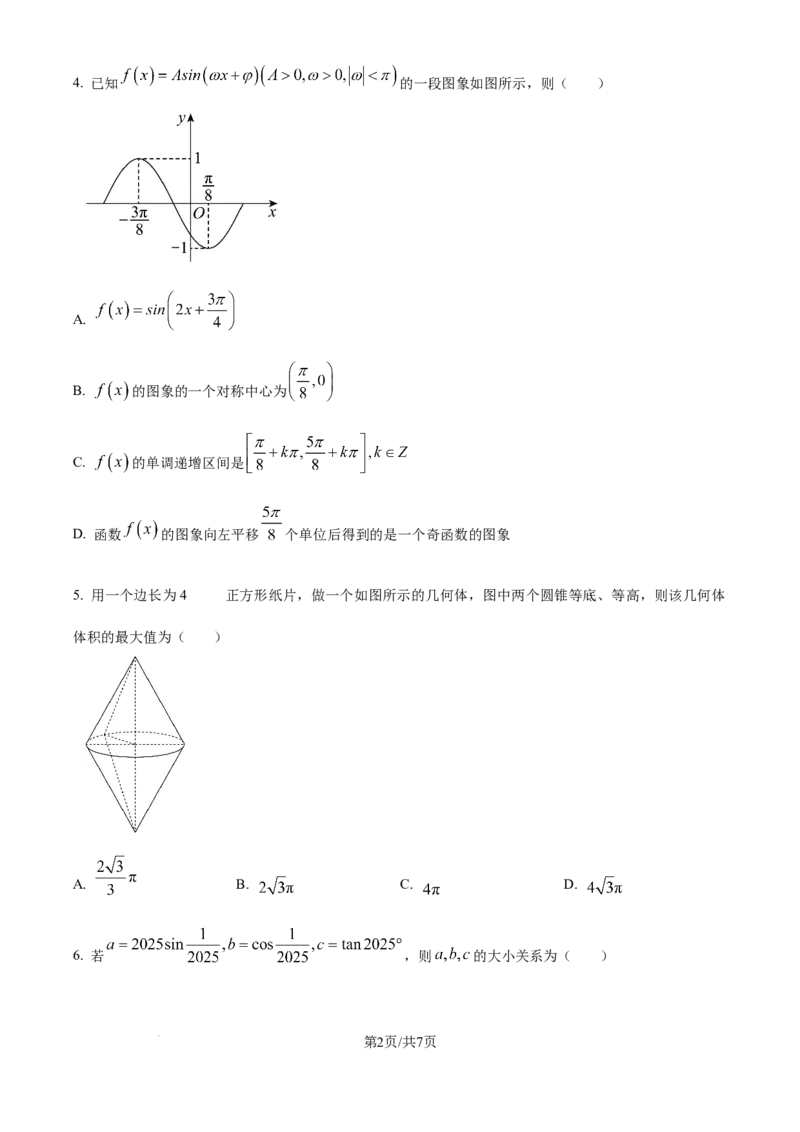
2. 函数 的部分图象大致为( )
A. B.
C D.
.
3. 椭圆 的两焦点为 , ,以 为边作正三角形,若椭圆恰好平分正三角形
的另两条边,则椭圆的离心率为( )
A. B. C. D.
第1页/共7页
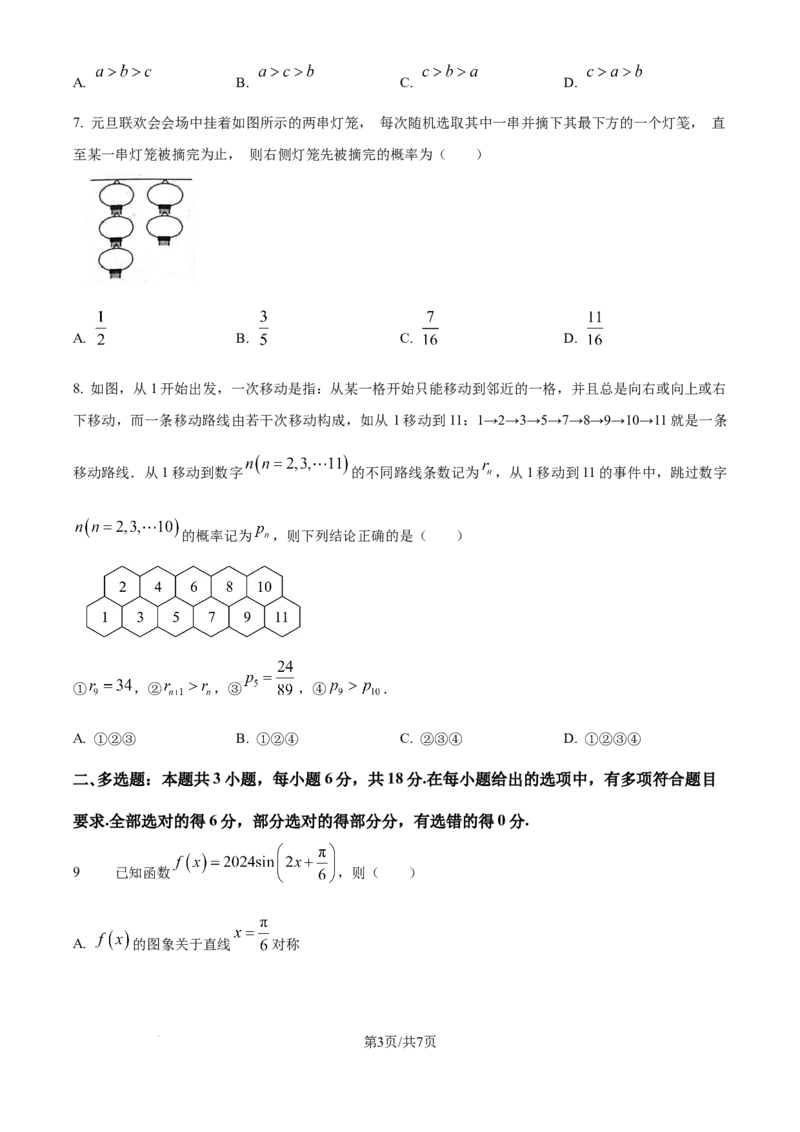
学科网(北京)股份有限公司4. 已知 的一段图象如图所示,则( )
A.
B. 的图象的一个对称中心为
C. 的单调递增区间是
D. 函数 的图象向左平移 个单位后得到的是一个奇函数的图象
的
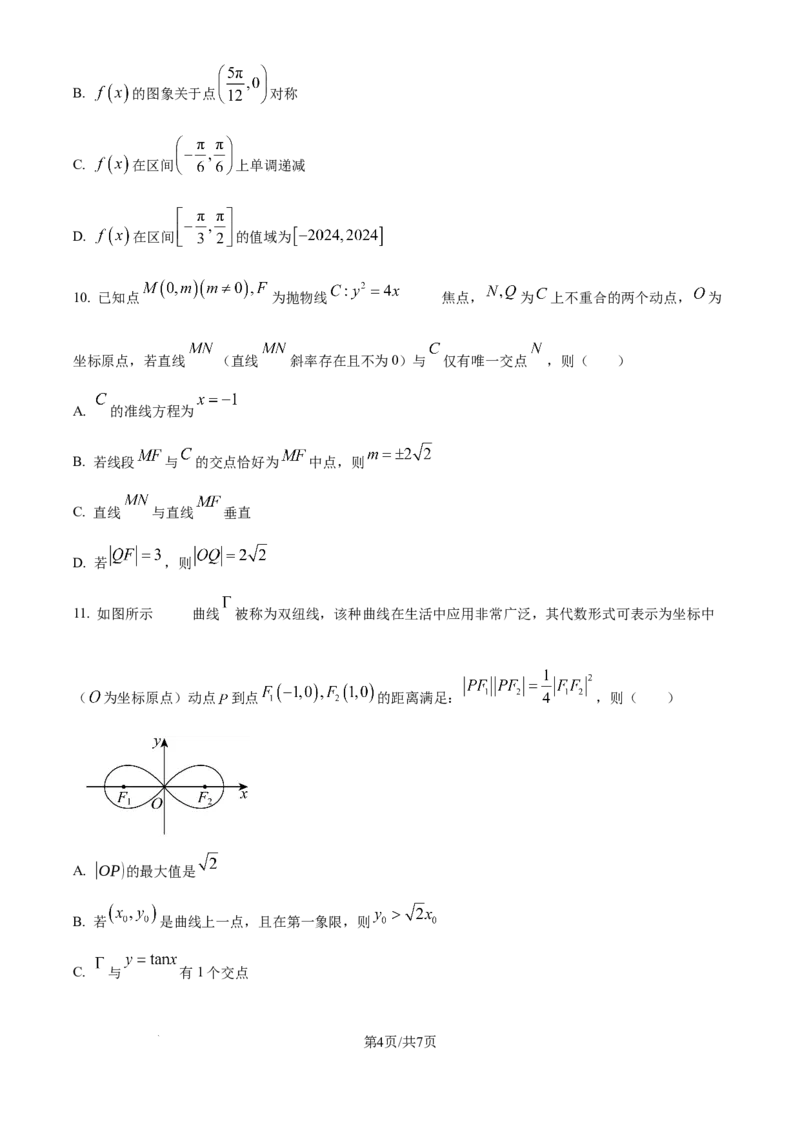
5. 用一个边长为4 正方形纸片,做一个如图所示的几何体,图中两个圆锥等底、等高,则该几何体
体积的最大值为( )
A. B. C. D.
6. 若 ,则 的大小关系为( )
第2页/共7页
学科网(北京)股份有限公司A. B. C. D.
7. 元旦联欢会会场中挂着如图所示的两串灯笼, 每次随机选取其中一串并摘下其最下方的一个灯笺, 直
至某一串灯笼被摘完为止, 则右侧灯笼先被摘完的概率为( )
A. B. C. D.
8. 如图,从1开始出发,一次移动是指:从某一格开始只能移动到邻近的一格,并且总是向右或向上或右
下移动,而一条移动路线由若干次移动构成,如从 1移动到11:1→2→3→5→7→8→9→10→11就是一条
移动路线.从1移动到数字 的不同路线条数记为 ,从1移动到11的事件中,跳过数字
的概率记为 ,则下列结论正确的是( )
① ,② ,③ ,④ .
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目
要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
.
9 已知函数 ,则( )
A. 的图象关于直线 对称
第3页/共7页
学科网(北京)股份有限公司B. 的图象关于点 对称
C. 在区间 上单调递减
D. 在区间 的值域为
的
10. 已知点 为抛物线 焦点, 为 上不重合的两个动点, 为
坐标原点,若直线 (直线 斜率存在且不为0)与 仅有唯一交点 ,则( )
A. 的准线方程为
B. 若线段 与 的交点恰好为 中点,则
C. 直线 与直线 垂直
D. 若 ,则
的
11. 如图所示 曲线 被称为双纽线,该种曲线在生活中应用非常广泛,其代数形式可表示为坐标中
( 为坐标原点)动点 到点 的距离满足: ,则( )
A. |OP)的最大值是
B. 若 是曲线上一点,且在第一象限,则
C. 与 有1个交点
第4页/共7页
学科网(北京)股份有限公司D. 面积的最大值是
三、填空题(本题共3小题,每小题5分,共15分)
12. 设抛物线 的焦点为 ,过点 作直线交抛物线于 , 两点,若 ,
,则 ___________.
13. 若曲线 在点 处的切线与曲线 相切,则 ________.
14. 某射击比赛中,甲、乙两名选手进行多轮射击对决.每轮射击中,甲命中目标的概率为 ,乙命中目
标的概率为 .若每轮射击中,命中目标的选手得1分,未命中目标的选手得0分,且各轮射击结果相互
独立.则进行五轮射击后,甲的总得分不小于3的概率为__________.
四、解答题: 本题共 5 小题. 解答应写出文字说明、证明过程或演算步骤.
15. 在 中,a,b,c分别为角A,B,C的对边,已知 ,且 .
(1)求角A的大小;
(2)求 面积的最大值.
16. 已知数列{a}的前n项和为S,a=2,a =2S+2.
n n 1 n+1 n
(1)求数列{a}的通项公式;
n
(2)若2b=3na,求数列{b}的前n项和T.
n n n n
17. 在 中,角 的对边分别为 的面积为 ,已知 .
(1)求角 ;
(2)若 的周长为 ,求 的最大值.
18. 正四棱柱 中 ,点 分别在 上,且 四点共面.
第5页/共7页
学科网(北京)股份有限公司(1)若 ,记平面 与底面的交线为 ,证明: ;
(2)已知 ,若 ,求四边形 面积的最大值.
19. 在高中数学教材苏教版选择性必修2上阐述了这样一个问题:假设某种细胞分裂(每次分裂都是一个
细胞分裂成两个)和死亡的概率相同,如果一个种群从这样的一个细胞开始变化,那么这个种群最终灭绝
的概率是多少?在解决这个问题时,我们可以设一个种群由一个细胞开始,最终灭绝的概率为 ,则从一
个细胞开始,它有 的概率分裂成两个细胞,在这两个细胞中,每个细胞灭绝的概率都是 ,两个细胞最
终都走向灭绝的概率就是 ,于是我们得到: ,计算可得 ;我们也可以设一个种群由
一个细胞开始,最终繁衍下去的概率为 ,那么从一个细胞开始,它有 的概率分裂成两个细胞,在这两
个细胞中,每个细胞繁衍下去的概率都是 ,两个细胞最终都走向灭绝的概率就是 ,于是我们得
到: ,计算可得 .根据以上材料,思考下述问题:一个人站在平面直角坐标系
的点 处,他每步走动都会有 的概率向左移动1个单位,有 的概率向右移动一个
单位,原点 处有一个陷阱,若掉入陷阱就会停止走动,以 代表当这个人由 开始,最终掉
第6页/共7页
学科网(北京)股份有限公司入陷阱的概率.
(1)若这个人开始时位于点 处,且 .
(ⅰ)求他在5步内(包括5步)掉入陷阱的概率;
(ⅱ)求他最终掉入陷阱的概率 ;
(ⅲ)已知 ,若 ,求 ;
(2)已知 是关于 的连续函数.
(ⅰ)分别写出当 和 时, 的值(直接写出即可,不必说明理由);
(ⅱ)求 关于 的表达式.
第7页/共7页
学科网(北京)股份有限公司