文档内容
高二物理参考答案(附中版)-(这是边文,请据需要手工删加)
湖南师大附中 2025—2026 学年度高二第一学期第一次大练习
物理参考答案
一、单项选择题(本题共 6 小题,每小题 4 分,共 24 分。在每小题给出的四个选项中,
只有一项是符合题目要求的)
题号 1 2 3 4 5 6
答案 D B D C A C
1.D 【解析】事故中气囊对头部的作用力与头部对气囊的作用力大小相等,方向相反,
且作用时间相等,所以,可知事故中气囊对头部的冲量与头部对气囊的冲量大小相等,方向
相反,故 A 错误;有无安全气囊司机初动量和末动量均相同,所以动量的改变量也相同,故
B 错误;在安全气囊的缓冲作用之下,司机的动能最终全部转换为内能,故 C 错误;因为安
全气囊充气后面积增大,司机的受力面积也增大,在司机挤压气囊作用过程中由于气囊的缓
冲故增加了作用时间,故 D 正确。
2.B 【解析】电动机正常工作时发热功率为 Pr =I2r=0.5 W,故 A 错误;根据闭合
0 0
电路欧姆定律有 E=U+I′r,小灯泡的电流为 I =I′-I,小灯泡额定功率为 P=UI ,代入数
L L
据解得 P=8 W,故 B 正确;电源的输出功率为 P′=UI′=16 W,故 C 错误;电动机正常工作
时其输出的机械功率为 P″=UI-Pr =7.5 W,故 D 错误。
0
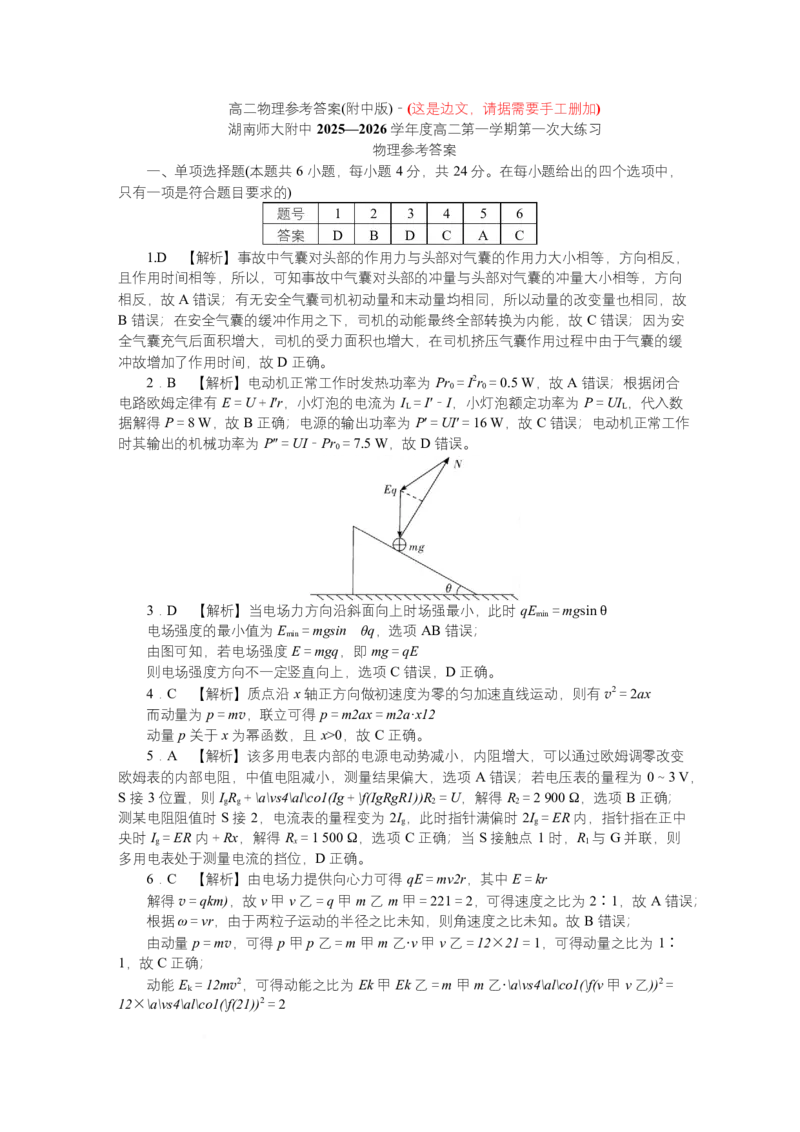
3.D 【解析】当电场力方向沿斜面向上时场强最小,此时 qE =mgsin θ
min
电场强度的最小值为 E =mgsin θq,选项 AB 错误;
min
由图可知,若电场强度 E=mgq,即 mg=qE
则电场强度方向不一定竖直向上,选项 C 错误,D 正确。
4.C 【解析】质点沿 x 轴正方向做初速度为零的匀加速直线运动,则有 v2=2ax
而动量为 p=mv,联立可得 p=m2ax=m2a·x12
动量 p 关于 x 为幂函数,且 x>0,故 C 正确。
5.A 【解析】该多用电表内部的电源电动势减小,内阻增大,可以通过欧姆调零改变
欧姆表的内部电阻,中值电阻减小,测量结果偏大,选项 A 错误;若电压表的量程为 0~3 V,
S 接 3 位置,则 IR+\a\vs4\al\co1(Ig+\f(IgRgR1))R =U,解得 R=2 900 Ω,选项 B 正确;
g g 2 2
测某电阻阻值时 S 接 2,电流表的量程变为 2I,此时指针满偏时 2I=ER 内,指针指在正中
g g
央时 I=ER 内+Rx,解得 R=1 500 Ω,选项 C 正确;当 S 接触点 1 时,R 与 G 并联,则
g x 1
多用电表处于测量电流的挡位,D 正确。
6.C 【解析】由电场力提供向心力可得 qE=mv2r,其中 E=kr
解得 v=qkm),故 v 甲 v 乙=q 甲 m 乙 m 甲=221=2,可得速度之比为 2∶1,故 A 错误;
根据ω=vr,由于两粒子运动的半径之比未知,则角速度之比未知。故 B 错误;
由动量 p=mv,可得 p 甲 p 乙=m 甲 m 乙·v 甲 v 乙=12×21=1,可得动量之比为 1∶
1,故 C 正确;
动能 E=12mv2,可得动能之比为 Ek 甲 Ek 乙=m 甲 m 乙·\a\vs4\al\co1(\f(v 甲 v 乙))2=
k
12×\a\vs4\al\co1(\f(21))2=2可得动能之比为 2∶1,故 D 错误。
二、多项选择题(本题共 4 小题,每小题 5 分,共 20 分。在每小题给出的四个选项中,
有多项符合题目要求,全部选对的得 5 分,选对但不全的得 3 分,有选错的得 0 分)
题号 7 8 9 10
答案 AC AD BD BD
7.AC 【解析】从爆炸后到落地,碎块 A、B 均做平抛运动,设两碎块落地时间均为 t,
则
IAIB=mAgtmBgt=21,A 正确;
爆炸时,水平方向根据动量守恒定律可知 m v -m v =0
A A B B
爆炸后两碎块均做平抛运动,下落高度相同,两碎块落地时间相等,则 xAxB=vAvB=
mBmA=12
A、B 的水平位移之比为 1∶2,而从爆炸瞬间到落地,下落高度相同,两碎块的位移之
比不等于 1∶2,B 错误;
xAxB=\rc\)(\a\vs4\al\co1(5 s-t))v 声\b\lc\(\rc\)(\a\vs4\al\co1(6 s-t))v 声=12,解得 t=4 s
则碎块 A 的水平位移 x =\rc\)(\a\vs4\al\co1(5 s-4 s)×340 m/s=340 m,碎块 B 的水平位
A
移 x =\rc\)(\a\vs4\al\co1(6 s-4 s)×340 m/s=680 m
B
则爆炸后两碎块落地点之间的水平距离为 340 m+680 m=1 020 m
碎块 A 的初速度为 v =xAt=85 m/s,C 正确,D 错误。
A
8.AD 【解析】设小球在 MN 中间的任意位置 C 时,此时 BC 两点水平方向的距离不
变,则此时小球对杆的弹力 F =kx·cos θ=kL=mg
N
则摩擦力始终为 f=μF =12mg,即从 M 到 N 摩擦力做功为 W=-fh=-12mgh,选项 A
N f
正确;
从 M 到 N 由能量关系可知 mgh+W +W=0,即弹性绳对小球做的功为-12mgh,选项
弹 f
B 错误;
小球下滑过程中弹性绳的弹力大于 mg,则弹性绳对小球的冲量大于 mgt,选项 C 错误;
小球下落 L2 时,弹性绳的伸长量ΔL=\rc\)(\a\vs4\al\co1(\f(L2)))2=5)2L
弹力大小为 F=kΔL=5)2mg
此时弹力沿竖直向上的分量为 F=Fcos α=5)2mg·12\r(52=12mg
y
则此时 f+F=mg,即竖直方向合力为零,加速度为零,速度最大,选项 D 正确。
y
9.BD 【解析】点电荷 P 在 xOy 平面内绕 x 轴上固定的点电荷 M 做逆时针方向的低速
椭圆运动,两者为吸引力,若 P 为负电荷,则点电荷 M 为正电荷,则 A 点的电势比 B 点的
电势低。故 A 错误;两点电荷为吸引力,当 P 沿 E、A、C 运动时,速度与电场力的夹角先
为钝角后为锐角,所以电场力先做负功后做正功。故 B 正确;由对称性可知,点电荷 P 在
CD 上任一点的电势能比在 EF 点上任一的电势能小,由能量守恒可知,点电荷 P 点 CD 上任
一点的动能比在 EF 点上任一点的动能大,即在 CD 上的平均速率比在 EF 上的大,而 CD 与
EF 的长度相等,根据 t=sv,可知 P 从 C 运动到 D 的时间小于从 E 运动到 F 的时间。故 C
错误;若点电荷 M 到坐标原点的距离与半长轴之比为 2∶3,则点电荷 M 到 A、B 两点的距
离之比为 5∶1,设 A、B 两处的曲率圆半径均为 r(对称性),则在 A 点,kq1q2AM2=m2Avr。
在 B 点 kq1q2BM2=m2Bvr,解得 v ∶v =BM∶AM=1∶5。可得 P 在 A、B 两点的速度之比
A B
为 1∶5。故 D 正确。
10.BD 【解析】由题可知,液滴处于静止状态时 U0dq=mg
电容器电压增加ΔU,油滴开始向上以加速度 a 运动 U0+ΔU1dq-mg=ma
1
电容器电压减少ΔU,加速度大小变为 3a 向下 mg-ΔU1+U0-ΔU2dq=3ma
2
以上式子联立可得ΔU1ΔU2=14,A 错误;设向上为正方向,在经过Δt 后,油滴的位移 x=12aΔt21,此时的速度为 v=aΔt
1 1 1
当再经过Δt 时,Δt 时间的位移 x=vΔt-12×3aΔt22,油滴回到初始位置则有 0=
2 2 2 2
x+x
1 2
联立可以得出Δt=Δt,B 正确;
1 2
Δt 时间末的速度 v=aΔt,再经过Δt 时间后的速度 v=v-3aΔt
1 1 2 2 2
因为Δt=Δt,所以 v=-2aΔt
1 2 2 1
因此油滴的动量变化量之比为\f(mvm(v2-v)))=13,故 D 对,C 错误。
三、实验题(本大题共两小题,11 题 8 分,12 题 6 分,共 14 分)
11. (1)0.515(2 分 ) (2)dt(2 分 ) \rc\)(\a\vs4\al\co1(M+ m))
d22\b\lc\(\rc\)(\a\vs4\al\co1(M-m))Ht2(2 分) (3)9.81(2 分)
【解析】(1)根据游标卡尺的读数规律,该游标卡尺的读数为 5 mm+0.05×3 mm=5.15
mm=0.515 cm
(2)根据光电门的测速原理,重锤 1 通过光电门时的速度大小为 v=dt
对 重 锤 1 与 重 锤 2 构 成 的 系 统 进 行 分 析 , 根 据 系 统 机 械 能 守 恒 定 律 有 \
rc\)(\a\vs4\al\co1(M- m)gH= 12\rc\)(\a\vs4\al\co1(M+ m)v2, 其 中 v= dt, 解 得 g= \
rc\)(\a\vs4\al\co1(M+m))d22\b\lc\(\rc\)(\a\vs4\al\co1(M-m))Ht2
(3)由于γ是只与圆柱体表面动摩擦因数有关的常数,且有 a=\rc\)(\a\vs4\al\co1(β-γ)g=
gβ-gγ
取表格从左至右四组数据分别为 a,a,a,a 和对应的β,β,β,β
1 2 3 4 1 2 3 4
利用表格中的数据,根据逐差法有 a+a-a-a=\rc\)(\a\vs4\al\co1(β4+β3-β2-β1)g
4 3 2 1
带入数据可则重力加速度 g=9.81 m/s2
12.(1)A(2 分) (2)1b(2 分) (3)R0n-1(2 分)
【解析】(1)为了保护电路,闭合开关前,金属夹置于电阻丝的最大阻值处,由图可知,
应该置于 A 端。
(2)对于电路图(a),根据闭合电路欧姆定律有 U=E-Ir
设金属丝的电阻率为ρ,横截面积为 S,结合欧姆定律和电阻定律 I=UR,R=ρLS
联立可得 U=E-USρLr,整理可得 1U=1E+SrEρ·1L
对于电路图(b),根据闭合电路欧姆定律有 U=E-I(r+R)
0
结合欧姆定律和电阻定律 I=UR,R=ρLS
联立后整理 1U=1E+S(r+R0)Eρ·1L
可知图线的纵轴截距 b=1E,解得 E=1b
(3)由题意可知 k=SrEρ,k=S(r+R0)Eρ,又 k2k1=n,联立解得 r=R0n-1
1 2
四、解答题(本大题共 3 小题,13 题 12 分,14 题 14 分,15 题 16 分,共 42 分)
13.(1)E=6 V,r=2 Ω,R=2 Ω(3 分) (2)P=2.25 W(4 分) (3)Q=2.1×10-5 C(5 分)
1
【解析】(1)依题开关 S 闭合、S 断开,根据闭合电路欧姆定律 E=U+Ir
1
结合图像,得
E=0.5r+5,E=1.5r+3,解得 E=6 V,r=2 Ω(2 分)
图像可知,当滑动变阻器的滑片滑到 b 处时,R 电压为 3 V,流过 R 电流为 1.5 A,故
1 1
R=UI=31.5 Ω=2 Ω(1 分)
1
(2)将 R 等效为电源内阻一部分,故电源等效内阻 r =R+r=4 Ω
1 等效 1
此时外电路只有滑动变阻器,结合闭合闭合电路欧姆定律可知,滑动变阻器消耗功率
P=\a\vs4\al\co1(\f(ER 滑+r 等效))2R =E2\b\lc\(\rc\)(\a\vs4\al\co1(R 滑-r 等效)R 滑
滑
可知 R =r 时,功率最大,即 P=E24r 等效=624×4 W=2.25 W(4 分)
滑 等效
(3)结合图像当滑动变阻器的滑片置于 a 端时,外电阻R =UI=50.5 Ω=10 Ω,R =R+R ,解得 R =8 Ω(1 分)
外 外 1 滑 滑
将滑动变阻器的滑片置于中间,电路稳定后,此时电容器两端电压为滑动变阻器电压
U =ER 滑 2×R 滑 2=62+2+4×4 V=3 V(1 分)
C1
将滑动变阻器的滑片置于中间,电路稳定后,闭合开关 S,电路再次稳定后,干路电流
1
I′=ER2×\b\lc\(\rc\2))R 滑 2)=1.2 A
故通过 R 的电流为 I =I′2=0.6 A(1 分)
1 R1
此时电容器两端电压为 R 两端电压,又因为极板间所带正负电荷与之前相反,即
1
U =I ×R=-1.2 V(1 分)
C2 R1 1
故求通过电阻 R 的电荷量 Q=C(U -U ),解得 Q=2.1×10-5 C(1 分)
3 C1 C2
14.(1)v=10gL(4 分) (2)v =gL(5 分) (3)-83mgL(5 分)
0 min
【解析】(1)将重力与电场力合成一个力,即等效重力,根据题意可知二者合力为 G′=\
rc\)(\a\vs4\al\co1(\f(\r(3)mgq)·q))2+\b\lc\(\rc\)(\a\vs4\al\co1(mg))2=2mg(1 分)
设重力与电场力的合力方向与竖直方向的夹角为θ,则 tan θ=Eqmg=3,可知θ=60°
小球恰能做完整的圆周运动时,在“等效最高点”速度最小,在“等效最高点”有 2mg
=mv2L
可得 v=2gL(1 分)
从 M 点到等效最高点有-mg·2Lcos 60°-Eq·2Lsin 60°=12mv2-12mv20(1 分)
解得 v=10gL(1 分)
0
(2)细线断裂后,小球相对合力方向做类斜抛运动,当小球在合力方向上的分速度为 0 时
,合速度最小,从 M 到 B,由动能定理有-mg\rc\)(\a\vs4\al\co1(L+Lcos 60°)-EqLsin 60°=
12mv2B-12mv20(2 分)
解得 v =2gL(2 分)
B
则最小速度 v =v cos 60°=gL(1 分)
min B
(3)从细线断裂到小球的电势能与 B 点电势能相等的过程中,电场力做功为零,即相当于
B 点水平方向的速度等大反向,则水平方向有 v =a′t′,qE=ma′(2 分)
B
竖直方向有 H=12g\rc\)(\a\vs4\al\co1(2t′)2(2 分)
根据 W=mgH=-ΔE,联立解得ΔE=-83mgL(1 分)
p p
15.(1)TeU0m)(4 分) (2)L(4 分)
(3)①2(2 分),4eU(2 分),2L(2 分) ②20e2UT28md2(2 分)
0
【解析】(1)根据图乙可知,为了达到同步加速,电子在圆筒中做匀速直线运动,运动的
时间均为 T2,电子加速两次过程,根据动能定理有 2eU=12mv22(2 分)
0
第 2 个金属圆筒的长度 s=v·T2,解得 s=TeU0m)(2 分)
2 2 2
(2)电子整个加速过程,根据动能定理得 4eU=12mv24
0
解得 v=8U0em)(1 分)
4
电子在两极板之间偏转过程,根据类平抛运动规律有 L=vt,y=12at21
41 1
其中 a=8U0e2mL,解得 y=L4(1 分)
1
射出极板后电子做匀速直线运动,沿轴线方向有 1.5L=vt
42
沿竖直方向 y=vt,v=at,解得 y=3L4(1 分)
2 y2 y 1 2
电子打在荧光屏的位置与 O 点间的距离为 Y=y+y=L(1 分)
1 1 2
(3)①电子通过 n 个圆筒后,根据动能定理有 neU=12mv2n
0
电子在两极板之间偏转过程,根据类平抛运动规律有 L=vt,y=12at2n
nn n
令电子打在荧光屏上的动能为 E,根据动能定理有 e·8U02Ly =E-12mv2n
k n k
解得 E=\a\vs4\al\co1(n+\f(4n))eU
k 0
根据数学函数规律可知,当 n 等于 2 时,电子打在荧光屏上的动能最小,动能最小值为E =4eU
kmin 0
电子通过 2 个圆筒加速后在两极板之间偏转过程,根据类平抛运动规律有 L=vt,y=
23 3
12at23
解得 y=L2
3
射出极板后电子做匀速直线运动,沿轴线方向有 1.5L=vt,沿竖直方向 y=v t,v
24 4 y14 y1
=at
3
解得 y=3L2
4
电子打在荧光屏的位置与 O 点间的距离为 Y=y+y=2L
2 3 4
②由于保持圆筒长度、交变电压的变化规律不变,若考虑电子在间隙中的加速时间,则
粒子进入每级圆筒的时间都要延后一些,如果延后累计时间等于 T2,则电子再次进入电场时
将开始减速,此时的速度就是装置能够加速的最大速度。由于两圆筒间隙的电场可以近似看
为匀强电场,间距均为 d,粒子在电场中后一个加速过程可以看为前一加速过程的延续部分,
令经过 N 次加速,即经过 N 个圆筒达到最大动能,则有 Nd=vm2·T2
根据动能定理有 NeU=12mv2m-0,解得 v =eU0T2md
0 m
则最大动能为 E =12mv2m
km
解得 E =20e2UT28md2
km(这是边文,请据需要手工删加)