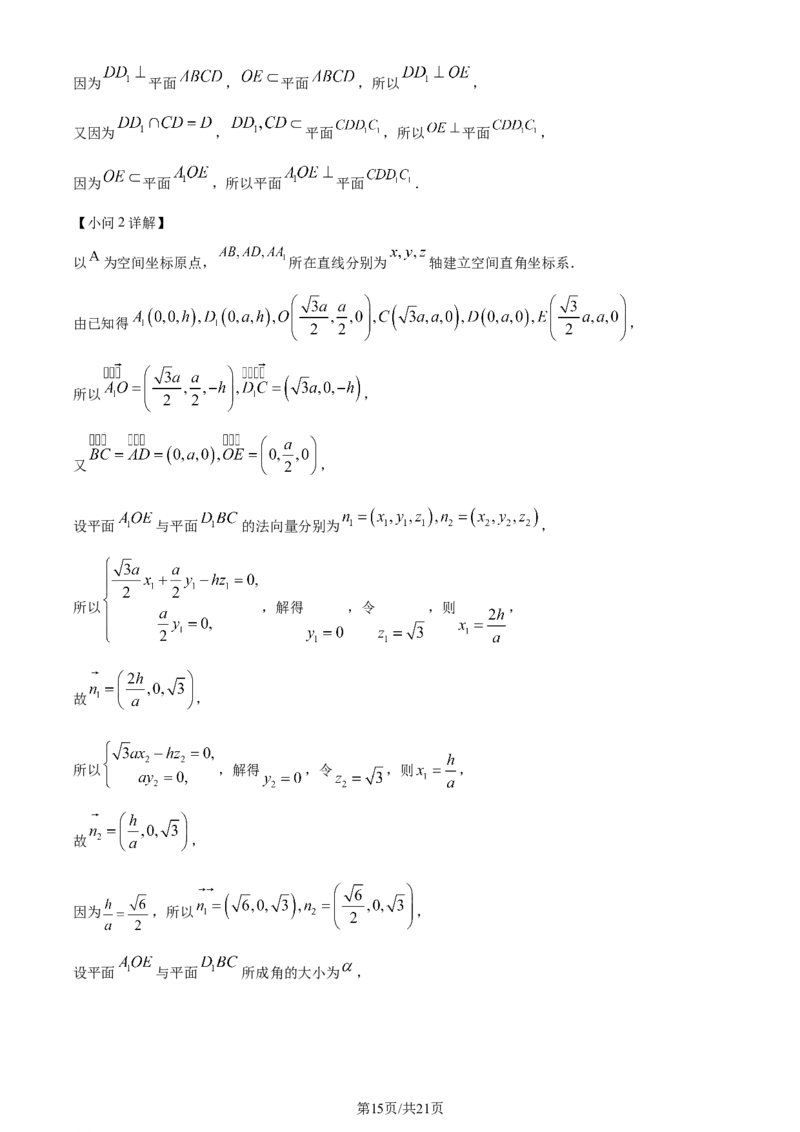文档内容
2024 届高三年级 TOP 二十名校冲刺一
数学
全卷满分150分,考试时间120分钟
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上,并将条形码粘贴在答题卡上
的指定位置.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改
动,用橡皮擦干净后,再选涂其它答案标号.回答非选择题时,将答案写在答题卡上,写在
本试卷上无效.
3.考试结束后,请将本试卷和答题卡一并交回.
4.本卷命题范围:高考范围.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项
是符合题目要求的.
1. 若复数 满足 ,则 ( )
A. B. C. D.
【答案】C
【解析】
【分析】利用复数除法法则计算出答案.
【详解】因为 ,所以 .
故选:C.
2. 已知集合 ,则 中元素的个数为( )
A. 9 B. 8 C. 5 D. 4
【答案】B
【解析】
【分析】利用列举法表示出集合A,再求出并集即可得解.
【详解】依题意,解不等式 ,得 , ,
第1页/共21页
学科网(北京)股份有限公司而 ,因此 ,
所以 中元素的个数为8.
故选:B
3. 若 ,则“ ”是“ ”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
【答案】C
【解析】
【分析】构造函数 ,根据函数单调性得到 ,故 .
【详解】构造函数 ,则 在 上单调递增,
所以 .
故选:C.
4. 函数 与直线 相切于点 ,则点 的横坐标为( )
A. B. 1 C. 2 D.
【答案】B
【解析】
【分析】设出 ,求导,直线 的斜率为 ,根据导数的几何意义得到方程,求出横坐标
【详解】设函数 与直线 相切于点 ,
直线 的斜率为 ,
,所以 ,所以 .
故选:B.
5. 设 ,则( )
第2页/共21页
学科网(北京)股份有限公司A. B.
C. D.
【答案】C
【解析】
【分析】根据指数幂与对数的运算性质,分别求得 的取值范围,即可求解.
详解】由 ,
【
即 ,所以 .
故选:C.
6. 在 中,若 ,则 的形状是( )
A. 等腰三角形 B. 直角三角形 C. 等腰直角三角形 D. 等腰或直角三角形
【答案】D
【解析】
【分析】利用余弦定理将 化简为 ,从而可求解.
【详解】由 ,得 ,
化简得 ,
为
当 时,即 ,则 直角三角形;
当 时,得 ,则 为等腰三角形;
综上: 为等腰或直角三角形,故D正确.
故选:D.
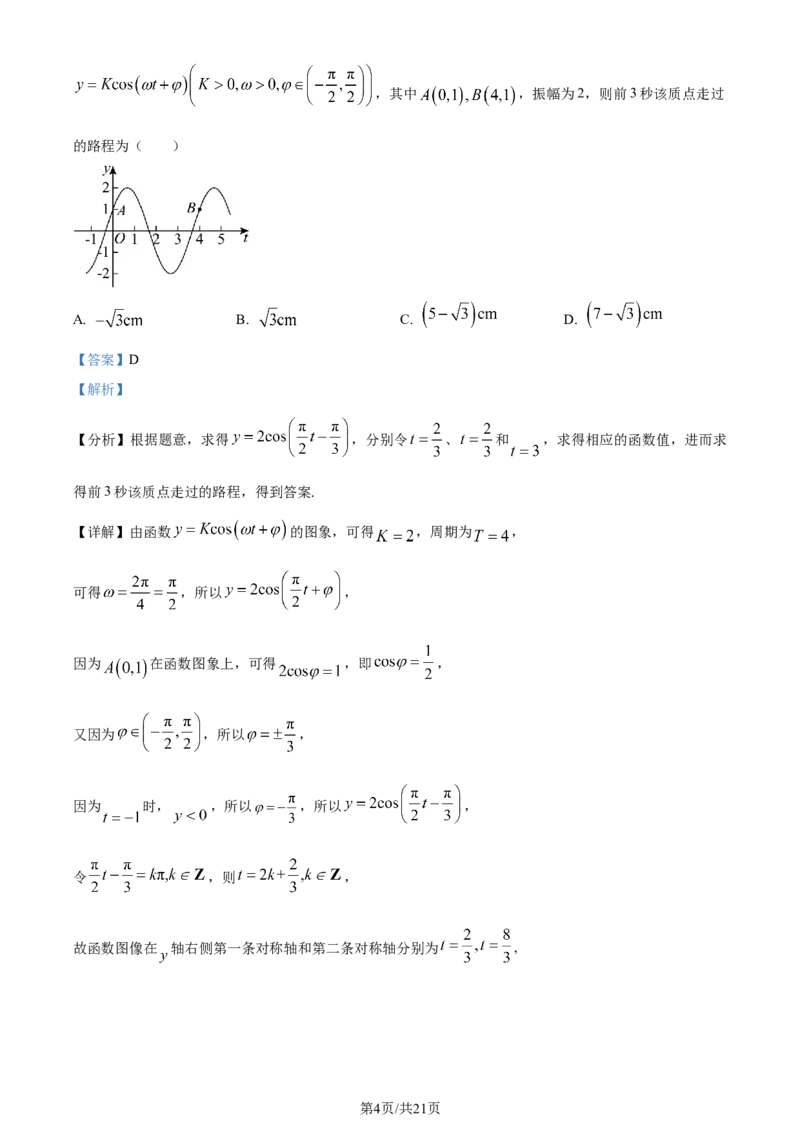
7. 如图是某质点作简谐运动的部分图象,位移 (单位: )与时间 (单位: )之间的函数关系式是
第3页/共21页
学科网(北京)股份有限公司,其中 ,振幅为2,则前3秒该质点走过
的路程为( )
A. B. C. D.
【答案】D
【解析】
【分析】根据题意,求得 ,分别令 、 和 ,求得相应的函数值,进而求
得前3秒该质点走过的路程,得到答案.
【详解】由函数 的图象,可得 ,周期为 ,
可得 ,所以 ,
因为 在函数图象上,可得 ,即 ,
又因为 ,所以 ,
因为 时, ,所以 ,所以 ,
令 ,则 ,
故函数图像在 轴右侧第一条对称轴和第二条对称轴分别为 ,
第4页/共21页
学科网(北京)股份有限公司令 ,则 ;令 ,则 ;
令 ,则 ,
所以质点在 的路程分别 ,
所以前3秒该质点走过的路程为 .
故选:D
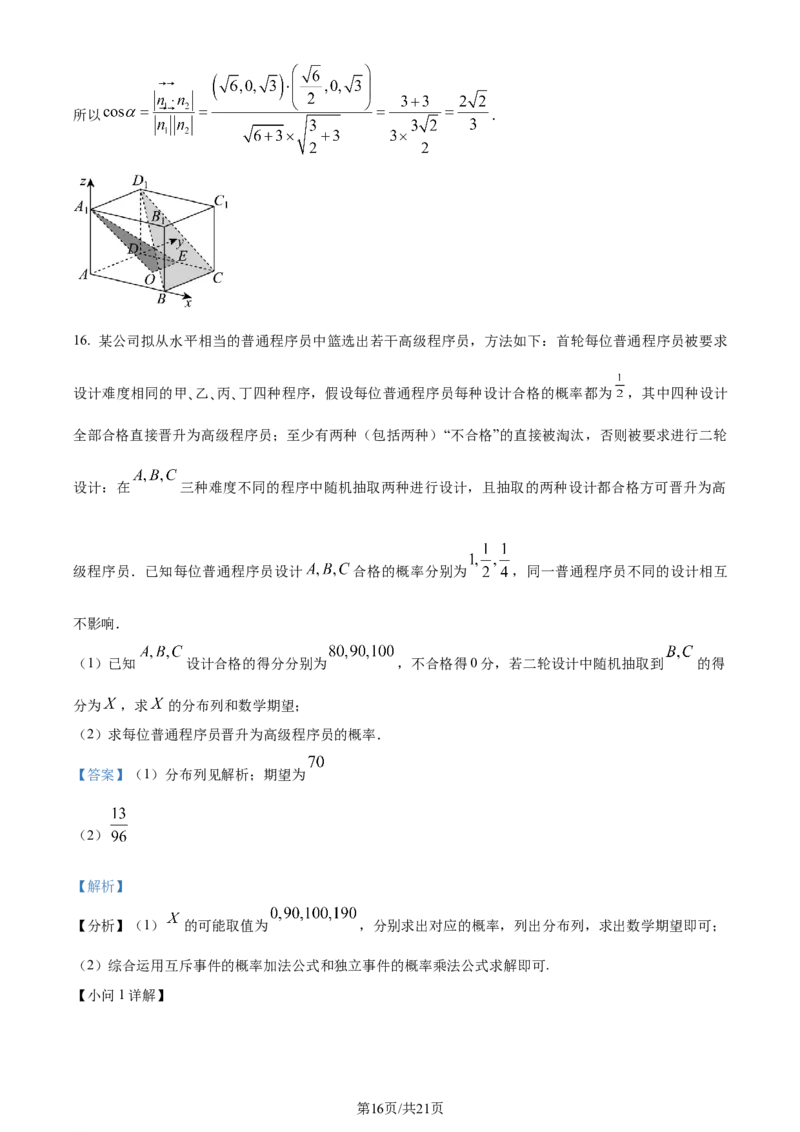
8. 已知点 在水平面 内,从 出发的三条两两垂直的线段 位于 的同侧,若 到
的距离分别为 ,则 的值为( )
A. 1 B. C. D. 2
【答案】A
【解析】
【分析】以 为空间的一个基底,由此表示出平面 的单位法向量,再利用数量积的运算律
求解即得.
【详解】由 两两垂直,取空间的一个基底 ,
设 是平面 的一个单位法向量,依题意,可使 与 的夹角都是锐角,
则存在唯一的有序实数组 ,使得 ,
显然 在 方向上的投影向量的长度分别为 ,
于是 ,即 ,则 ,即 ,
同理 ,因此 ,
第5页/共21页
学科网(北京)股份有限公司而 ,所以 ,
因此 ,
所以 .
故选:A
【点睛】关键点点睛:选定空间不共面的三个向量作基向量,并用它们表示出指定的向量,是用向量解决
立体几何问题的关键,解题时应结合已知和所求观察图形,联想相关的运算法则和公式等,就近表示所需
向量.
二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多项符
合要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9. 某研究机构为了探究过量饮酒与患疾病 真否有关,调查了400人,得到如图所示的 列联表,其中
,则( )
患疾病 不患疾病 合计
过量饮酒
不过量饮酒
合计 400
参考公式与临界值表:
0.100 0.050 0.010 0.001
2.706 3.841 6.635 10.828
A. 任意一人不患疾病 的概率为0.9
B. 任意一人不过量饮酒的概率为
C. 任意一人在不过量饮酒的条件下不患疾病 的概率为
第6页/共21页
学科网(北京)股份有限公司的
D. 依据小概率值 独立性检验,认为过量饮酒与患疾病 有关
【答案】ACD
【解析】
【分析】先求出 ,利用古典概型概率公式求解判断AB,利用条件概率概念求解判断C,求
出 的观测值,即可判断D.
【详解】由已知得 ,又 ,所以 .
任意一人不患疾病 的概率为 ,所以A正确;
任意一人不过量饮酒的概率为 ,所以B错误;
任意一人在不过量饮酒的条件下不患疾病 的概率为 ,所以C正确;
对于D, 列联表如下:
患疾病 不患疾病 合计
过量饮酒 30 120 150
不过量饮酒 10 240 250
合计 40 360 400
则 的观测值 ,由于 ,
依据小概率值 的独立性检验,认为过量饮酒与患疾病 有关,所以D正确.
故选:ACD
10. 已知椭圆 的左,右焦点分别为 ,将 上所有点的横坐标与纵坐标分
别伸长到原来的 倍得到椭圆 ,则下列说法正确的是( )
第7页/共21页
学科网(北京)股份有限公司A. 若 ,则
B. 若 的离心率分别为 ,则
C. 若 的周长分别为 ,则
D. 若 的四个顶点构成的四边形面积为 ,则 的离心率为
【答案】AB
【解析】
【分析】利用糖水不等式判断选项A;根据椭圆离心率的定义式判断选项B;利用相似图形的相似比即可
判断出选项C;综合运用椭圆的几何性质和四边形的面积公式判断选项D即可.
【详解】设点 为椭圆 上任意一点,则由题意知 ,即 ,代入椭圆 的方程得
.所以椭圆 的方程为 .
因为 ,所以 ,所以 正确;
由已知得, ,所以 正确;
由已知得, ,其相似比为 ,所以 ,所以 ,因为 ,所以 错误;
设 ,因为 的四个顶点构成的四边形的面积为 ,所以 ,所以
,所以 ,所以 ,所以 (负
第8页/共21页
学科网(北京)股份有限公司舍),所以D错误.
故选: .
11. 将圆柱 的下底面圆 置于球 的一个水平截面内,恰好使得 与水平截面圆的圆心重合,圆柱
的上底面圆 的圆周始终与球 的内壁相接(球心 在圆柱 内部).已知球 的半径为3,
.若 为上底面圆 的圆周上任意一点,设 与圆柱 的下底面所成的角为 ,圆柱
的体积为 ,则( )
A. 可以取到 中的任意一个值
B.
C. 的值可以是任意小的正数
D.
【答案】BCD
【解析】
【分析】先画出平面图,得到圆柱的底面半径 ,高为 ,代入圆柱体积公式求解,再
令 ,利用导数求最值.
第9页/共21页
学科网(北京)股份有限公司【详解】
过R作圆柱 的轴截面 ,过O作 交圆柱轴截面的边于M,N,
由 与圆柱的下底面所成的角为 ,则 ,所以
,
即 ,故B正确;
当点P,Q均在球面上时,角 取得最小值,此时 ,所以 ,
所以 ,故A错误;
令 ,所以 ,
所以 ,另 ,
解得两根 ,
所以 ,
所以 在 时单调递减,
第10页/共21页
学科网(北京)股份有限公司所以 , ,故CD正确;
故选:BCD.
【点睛】关键点睛:本题主要考查运用导数求最值的方法,难度较大,解决问题的关键在于先画出平面图,
得到圆柱的底面半径 ,高为 ,代入圆柱体积公式求解,再令 ,利用导数求
最值.
三、填空题:本题共3小题;每小题5分,共15分.
12. 若 ,则 的值为__________.
【答案】
【解析】
【分析】利用向量夹角余弦公式进行求解.
【详解】 .
故答案为:
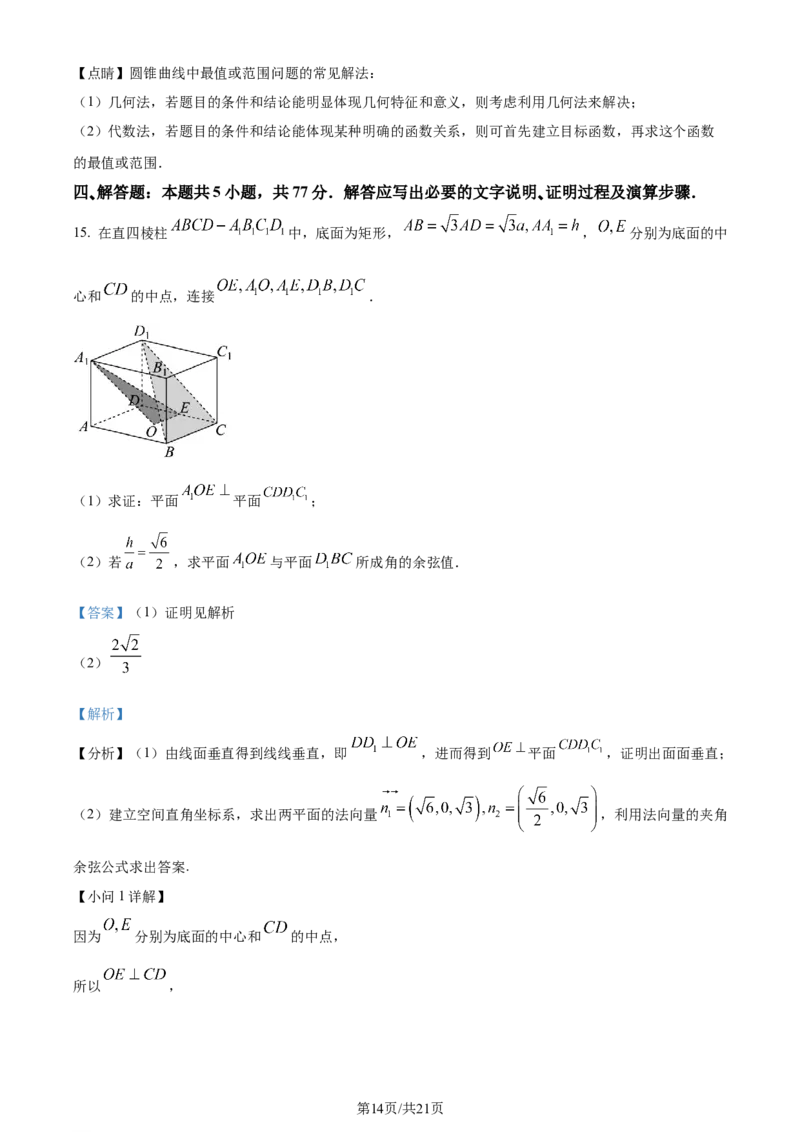
13. 如图是一个水平放置在某地的三棱台型集雨器,已知上、下底的面积分别为 和 ,高为 .
现在搜集到的雨水平面与上、下底面的距离相等,则该地的降雨量为______ .(降雨量等于集雨器中积
水体积除以集雨器口的面积)
【答案】
【解析】
【分析】将三棱台补成三棱锥 ,求得三棱锥 的体积为 ,再设 和
第11页/共21页
学科网(北京)股份有限公司的体积分别为 ,结合则 ,求得 和 ,根据 ,即可求解.
【详解】如图所示,将三棱台补成三棱锥 ,设三棱锥 的高为 ,
则 ,解得 ,所以三棱锥 的体积为 ,
再设 的体积分别为 ,
则 ,所以 ,所以 ,
同理 ,所以 ,
所以该地的降雨量为 .
故答案为: .
14. 若点 在抛物线 上运动,点 在圆 上运动, ,则 的最小
值为__________.
【答案】2
【解析】
第12页/共21页
学科网(北京)股份有限公司【 分 析 】 设 , 根 据 抛 物 线 焦 半 径 得 到 , 利 用 两 点 间 距 离 公 式 得 到
, 根 据 得 到 , 变 形 得 到
,利用基本不等式求出最小值.
【详解】抛物线 的焦点 的坐标为 ,准线方程为 ,
为圆 的圆心,圆的半径为 ,
设点 ,则由抛物线的定义得 ,
,
由三角形三边关系得到 ,当且仅当 共线时,等号成立,
所以 ,
令 ,则 ,
所以 ,
当且仅当 ,即 时等号成立,故 的最小值为2.
故答案为:2
第13页/共21页
学科网(北京)股份有限公司【点睛】圆锥曲线中最值或范围问题的常见解法:
(1)几何法,若题目的条件和结论能明显体现几何特征和意义,则考虑利用几何法来解决;
(2)代数法,若题目的条件和结论能体现某种明确的函数关系,则可首先建立目标函数,再求这个函数
的最值或范围.
四、解答题:本题共5小题,共77分.解答应写出必要的文字说明、证明过程及演算步骤.
15. 在直四棱柱 中,底面为矩形, , 分别为底面的中
心和 的中点,连接 .
(1)求证:平面 平面 ;
(2)若 ,求平面 与平面 所成角的余弦值.
【答案】(1)证明见解析
(2)
【解析】
【分析】(1)由线面垂直得到线线垂直,即 ,进而得到 平面 ,证明出面面垂直;
(2)建立空间直角坐标系,求出两平面的法向量 ,利用法向量的夹角
余弦公式求出答案.
【小问1详解】
因为 分别为底面的中心和 的中点,
所以 ,
第14页/共21页
学科网(北京)股份有限公司因为 平面 , 平面 ,所以 ,
又因为 , 平面 ,所以 平面 ,
因为 平面 ,所以平面 平面 .
【小问2详解】
以 为空间坐标原点, 所在直线分别为 轴建立空间直角坐标系.
由已知得 ,
所以 ,
又 ,
设平面 与平面 的法向量分别为 ,
所以 ,解得 ,令 ,则 ,
故 ,
所以 ,解得 ,令 ,则 ,
故 ,
因为 ,所以 ,
设平面 与平面 所成角的大小为 ,
第15页/共21页
学科网(北京)股份有限公司所以 .
16. 某公司拟从水平相当的普通程序员中篮选出若干高级程序员,方法如下:首轮每位普通程序员被要求
设计难度相同的甲、乙、丙、丁四种程序,假设每位普通程序员每种设计合格的概率都为 ,其中四种设计
全部合格直接晋升为高级程序员;至少有两种(包括两种)“不合格”的直接被淘汰,否则被要求进行二轮
设计:在 三种难度不同的程序中随机抽取两种进行设计,且抽取的两种设计都合格方可晋升为高
级程序员.已知每位普通程序员设计 合格的概率分别为 ,同一普通程序员不同的设计相互
不影响.
(1)已知 设计合格的得分分别为 ,不合格得0分,若二轮设计中随机抽取到 的得
分为 ,求 的分布列和数学期望;
(2)求每位普通程序员晋升为高级程序员的概率.
【答案】(1)分布列见解析;期望为
(2)
【解析】
【分析】(1) 的可能取值为 ,分别求出对应的概率,列出分布列,求出数学期望即可;
(2)综合运用互斥事件的概率加法公式和独立事件的概率乘法公式求解即可.
【小问1详解】
第16页/共21页
学科网(北京)股份有限公司的可能取值为 ,
由题意知, ,
,
的分布列为
0 90 100 190
.
【小问2详解】
因为同一普通程序员不同的设计相互不影响,所以每位普通程序员晋升为高级程序员的概率为
.
17. 在平面直角坐标系中,点 的坐标分别为 ,以 为圆心作一个半径为4的圆,
点 是圆上一动点,线段 的重直平分线与直线 相交于点 .
(1)求 的轨迹 的方程;
(2)已知 ,点 是轨迹 在第一象限内的一点, 为 的中点,若直线 的斜率为 ,
求点 的坐标.
【答案】(1)
(2)
【解析】
【分析】(1)利用垂直平分线的性质及双曲线的定义可得答案;
(2)利用中点公式和 的斜率为 建立方程组,求解方程组可得答案.
第17页/共21页
学科网(北京)股份有限公司【小问1详解】
由题意可知,点 在线段 的垂直平分线上,所以 ,
又点 是圆 上一动点,所以 .
①当 时, ;
②当 时, ,
所以 的轨迹 满足 ,
根据双曲线定义可知, 点的轨迹 是以 为左、右焦点,实轴长为 的双曲线,
可得 ,所以 的轨迹 的方程为 .
【小问2详解】
设 ,所以 ,
因为直线 的斜率为 ,所以 ,即 ,
与 联立解得 (舍去)或3.
所以点 的坐标为 .
18. 已知函数 .
(1)讨论函数 的单调性;
(2)当 时,求证: .
【答案】(1)答案见解析
(2)证明见解析
【解析】
第18页/共21页
学科网(北京)股份有限公司【分析】(1)求出导函数,然后根据 和 分类讨论,解导函数不等式即可求得单调区间;
(2)根据(1)的结论知 ,令 得 ,结合对数运算累加法即
可证明.
【小问1详解】
的定义域为 .
,
①当 时, 在 上单调递增;
②当 时, 时, 在 上是增函数.
时, 在 上是减函数,
时, 在 上是增函数.
【小问2详解】
由(1)得,当 时, , 在 上是减函数,
即当 时, ,所以 ,
令 得, ,即 ,
所以 ,得证.
19. 在等差数列 中,已知 成等差数列.
(1)求数列 的通项公式;
第19页/共21页
学科网(北京)股份有限公司(2)数列 是否为等比数列?若是求其前 项和,若不是,请说明理由;
(3)设 ,且 ,求 所有取值.
的
【答案】(1)
(2)是等比数列,
(3)
【解析】
【分析】(1)设等差数列 的首项为 ,公差为 ,依题意得到关于 、 的方程组,解得即可;
(2)根据等比数列的定义判断,再由等比数列求和公式计算可得;
( 3 ) 依 题 意 可 得 当 时 无 解 , 当 时 解 得 , 说 明
时无解,即可确定 的值.
【小问1详解】
设等差数列 的首项为 ,公差为 ,
因为 成等差数列,
所以 ,解得 ,
所以 .
【小问2详解】
因为 , ,
所以 是以 为首项, 为公比的等比数列,
第20页/共21页
学科网(北京)股份有限公司所以数列 的前 项和为 .
【小问3详解】
因为 ,所以 ,
因为 ,
所以 ,
当 时, 无解;
当 时,解得 或 (舍去);
当 时, ,即 ,
令 ,则 为关于 的单调递增函数,
因为 ,所以 ,
所以 无解,
所以 的取值为 ,
进一步得,当 时,对任意的正整数 ,
,
满足: ,
所以 的所有取值是 .
【点睛】关键点点睛:第三问由于 的任意性取特殊值确定 的值,再验证其合理性.
第21页/共21页
学科网(北京)股份有限公司