文档内容
宜宾市普通高中 2022 级第一次诊断性测试
数学参考答案及评分意见
一、选择题
题号 1 2 3 4 5 6 7 8 9 10 11
选项 A B C C A C D B ABC AC BCD
三、填空题:本题共4小题,每小题5分,共20分。
12. 13. 14.
四、解答题:本题共 小题,共 分。解答应写出文字说明,证明过程或演算步骤。
15.(13分) D 1 C 1
A B
(1)证明:连结 ,在 中, , 1 1
, , , M
所以 ,于是 ,
D
同理可证 ,又 C
O
A
所以 平面 ,又 平面 , B
所以平面 平面 ;··························································· 6分
(2)解:取 的中点 ,连结 ,
因为 ,
所以, ,
所以平面 与平面 的夹角为 ,····································10分
在 中, , ,
所以, ··························································· 12分
平面 与平面 的夹角的余弦值 .··················································· 13分
16.(15分)
解:(1)该射手恰好命中一次的概率
··········································6分
(2)该射手的总得分 的所有可能取值为:0,1,2,3,4····················7分
所以
一诊数学参考答案第1页共5页一诊数学参考答案第1页共5页
···································································12分
于是, 的分布列为
··································································································· 13分
所以, ··························15分
17.(15分)
解:(1) ······3分
所以
即 ,··········································································4分
又因为 ,所以 ···············································6分
所以 ······················································································7分
(2)在 中, ,即
所以 , ··························································9分
所以 ·····························10分
因为 ,所以 , ···································12分
设 ,于是 ···················14分
一诊数学参考答案第2页共5页一诊数学参考答案第2页共5页
可得: ·····································································15分
法二 由余弦定理可知: ,由几何图形可知( )
所以 易得 .
18.(17分)
{a
=
1 ¿{b
=
2
¿¿¿¿
¿
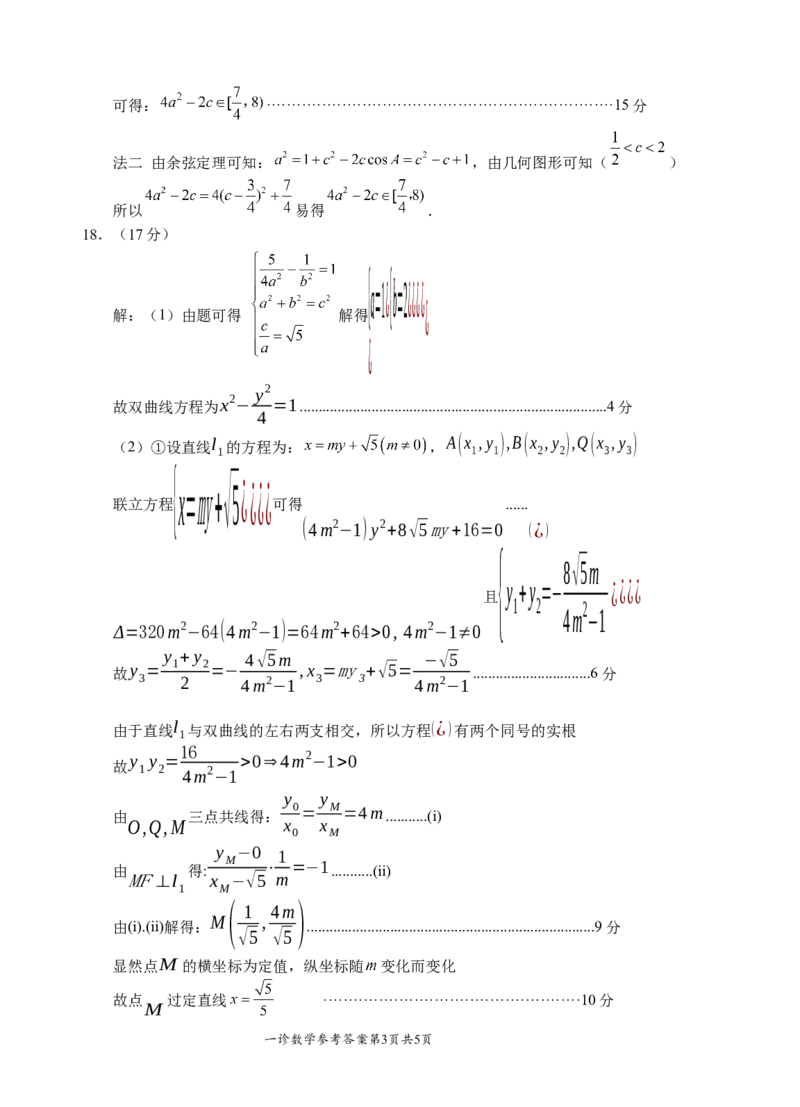
解:(1)由题可得 解得
¿
y2
故双曲线方程为x2 − =1.................................................................................4分
4
(2)①设直线l 的方程为: , A(x ,y ),B(x ,y ),Q(x ,y )
1 1 1 2 2 3 3
{x
=
my
+
√5¿¿¿¿
联立方程 可得 ......
(4m2 −1)y2 +8√5my+16=0 (¿)
{ 8√5m
y +y =− ¿¿¿¿
且
1 2 2
4m −1
Δ=320m2 −64(4m2 −1)=64m2 +64>0, 4m2 −1≠0
故y =
y
1
+y
2 =−
4√5m
,x =my +√5=
−√5
...............................6分
3 2 4m2 −1 3 3 4m2 −1
由于直线l 与双曲线的左右两支相交,所以方程(¿)有两个同号的实根
1
16
y y = >0⇒4m2 −1>0
故 1 2 4m2 −1
y y
由 三点共线得: 0 = M =4m...........(i)
O,Q,M x x
0 M
y −0 1
由 得: M ⋅ =−1 ...........(ii)
MF⊥l x −√5 m
1 M
1 4m
( )
M ,
由(i).(ii)解得: ............................................................................9分
√5 √5
显然点M 的横坐标为定值,纵坐标随 变化而变化
故点 过定直线 ···················································10分
M
一诊数学参考答案第3页共5页一诊数学参考答案第3页共5页
②由
⃗MN= ⃗MA+ ⃗MB可知,四边形MANB是平行四边形,
1 4m2
| − −√5|
所以 , d = √5 √5 = 4 √1+m2
S MANB =2S Δ =d M−l |AB| M−l 1 √1+m2 √5
MAB 1
8√1+m2 8(m2 +1)
|AB|= √1+m2 |y −y |= √1+m2 ⋅ = ,因为
1 2 |4m2 −1| 4m2 −1 4m2 −1>0
4
8(1+m2)
S = √1+m2 ⋅ . ................................................................................13
MANB √5 4m2 −1
分
令 ,则
t= √1+m2,m2 =t2 −1,t>1
4 5
令 f (t)= − (t>1)
t t3
则
所以 在 单调递增,在 单调递减,
f (t)
故 ..............................................................................15分
此时四边形 面积取到最小值为 ,
当且仅当 时取等号. ..... ...................... ...................................17
分
19.(17分)
解:(1)当 时, .
所以u'(x)<0⇒x>1,u'(x)>0⇒02,此时 f '(1)=2g(1)<0 ...........................................................................................7分
注意到当x→+∞时f '(x)→+∞,故f '(x)=0在(1,+∞)有一个根x
2
容易证明当a>2时lna [a2 −a+1−2(a−1)]= (a2 −3a+3)>0
a a a a
1
所以 在( ,1)上有一个根 ,故 恰有两个极值点,符合题意.
f '(x)=0 a x f (x)
1
综上实数a的取值范围为(2,+∞) .........................................................................................10
分
方法二:可用参变分离法求解,(阅卷时酌情给分.)
②由上面的讨论可知
0f (1)>0
,同理可得
f (x )