文档内容
绝密★启用前 { x+ 1 −2,x>1,
8. 已知函数 f (x)= x−1 若关于x的方程f(f(x))=m有五个不等的实数解,则m的
辽宁省名校联盟 2024 年高三 3 月份联合考试
2−2x,x≤1,
取值范围是
数学 A.(0,1) B.[1,2) C.(1,+∞) D.[0,2]
二、选择题:本题共3小题,每小题6分,共18分。在每小题给出的选项中,有多项符合题目
命题人:辽宁名校联盟试题研发中心 审题人:辽宁名校联盟试题研发中心
要求,全.部选对的得6分,部分选对的得部分分,有选错的得0分。
π
9.已知函数 f (x)=Asin(ωx+)(A⟩0,ω<0,| |< )的部分图像如图所示,则
❑ 2
本试卷满分150分,考试时间120分钟。
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。如需改
动,用橡皮擦干净后,再选涂其他答案标号。答非选择题时,将答案写在答题卡上。
A. f(x)的周期为6
写在本试卷上无效。
B. f(x+5)=f(5-x)
3.考试结束后,将本试卷和答题卡一并交回。
1
C.将f(x)的图像向右平移· 个单位长度后所得的图像关于原点对称
2
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一
项是符合题目要求的。 D. f(x)在区间[3,5]上单调递增
2−i
1. 在复平面内对应的点位于 10.已知抛物线C: y²=6x的焦点为F,O为坐标原点,倾斜角为θ的直线l过点 F 且与C 交于
4+3i
M,N两点,若△OMN的面积为 3√3,则
A.第一象限 B.第二象限 C.第三象限 D.第四象限
√3
2.已知集合 A=x|2x²−5x<0,B=x|−10,则 p为真命题的一个必要不充分条件是
11.已知数列{aₙ}的首项为a₁,且 a,+e⁴−4=7,则
A. a<5 B. a>5 C. a<4 D. a>4
A.存在 a₁ 使数列{aₙ}为常数列
4.某表彰会上3名男同学和4名女同学从左至右排成一排上台领奖,则女生甲与女生乙相
B. 存在 a₁使数列{aₙ}为递增数列
邻,且女生丙与女生丁相邻的排法种数为
C.存在 a₁ 使数列{aₙ}为递减数列
A.194 B.240 C.388 D.480
D.存在 a₁ 使得a₁≥a,恒成立
f (x)=log (x2−4x+7),
5.已知函数f(x+2)为偶函数,且当x≥2时, 1 若 f(a)>f(b),则
7 三、填空题:本题共3 小题,每小题5分,共15分。
A.(a+b-4)(a-b)<0 B.(a+b-4)(a-b)>0
12.已知向量a=(1,0),b=(-1,-2),若3a+2b与xa-4b共线,则x= .
C.(a+b+4)(a-b)<0 D.(a+b+4)(a-b)>0
13.小明所在的公司上午9:00上班,小明上班通常选择自驾、公交或地铁这三种方式.若小明选择自
m m
6.已知m>2n>0,则 + 的最小值为
m−2n n 驾,则从家里到达公司所用的时间(单位:分钟)服从正态分布 N₁(38,25);若小明选择地铁,则从
A.3+2√2 B.3−2√2 C.2+3√2 D.3√2−2 家里到达公司所用的时间(单位:分钟)服从正态分布 N₂(45,9);若小明选择公交,则从家里到
7.已知某圆锥的母线长为 3√5,底面积为 9π,记该圆锥的体积为 V,若用一个平行于圆锥
达公司所用的时间(单位:分钟)服从正态分布 N₂(36,16).若小明上午 8:12 从家里出发,则选
V
底面的平面截该圆锥,且截去一个体积为 的小圆锥,则剩余几何体的外接球的表面积 择 上班迟到的可能性最小.(填“自驾”“公交”或“地铁”)
27
为
参考数据:若 X∼N(μ,σ²),则 (μ−σ≤X≤μ+σ)≈68.3. P(μ−3σ≤X≤μ+3σ)≈99.7
A.60π B.40π C.30π D.20π
学科网(北京)股份有限公司x2 y2
14.已知双曲线 C. − =1(a⟩0,b>0)的左、右焦点分别为 F₁,F₁,记以 F₁F₂为直径的圆与
a2 b2
C 的渐近线在第一象限交于点 P,点 Q 为线段 PF₂ 与 C 的交点,O 为坐标原点,且
2⃗F Q=⃗F P+ 2⃗OF ,则C的离心率为 .
1 1 2
四、解答题:本题共5 小题,共77分。解答应写出文字说明、证明过程或演算步骤。
15.(13 分)
17.(15分)
已知在 △ABC中,内角 A,B,C所对的边分别为a,b,c,其中 a=4,4√3cosC=√3b−csin A.
如图,在平行六面体 ABCD−A₁B₁C₁D₁中,E在线段 A₁D₁上,且 ∠EDA=∠EAD,F,G分别
(1)求 A;
为线段BC,AD的中点,且底面 ABCD为正方形.
2√2
(2)已知直线 AM为. ∠BAC的平分线,且与BC交于点M,若 AM= ,求 △ABC的周长.
3 (1)求证:平面. BCC₁B₁⊥平 面E; FG
(2)若EF 与底面ABCD不垂直,直线 ED与平面EBC 所成角为 45°,且 EB=AB=2,求点 A 到平面
A₁B₁C₁D₁的距离.
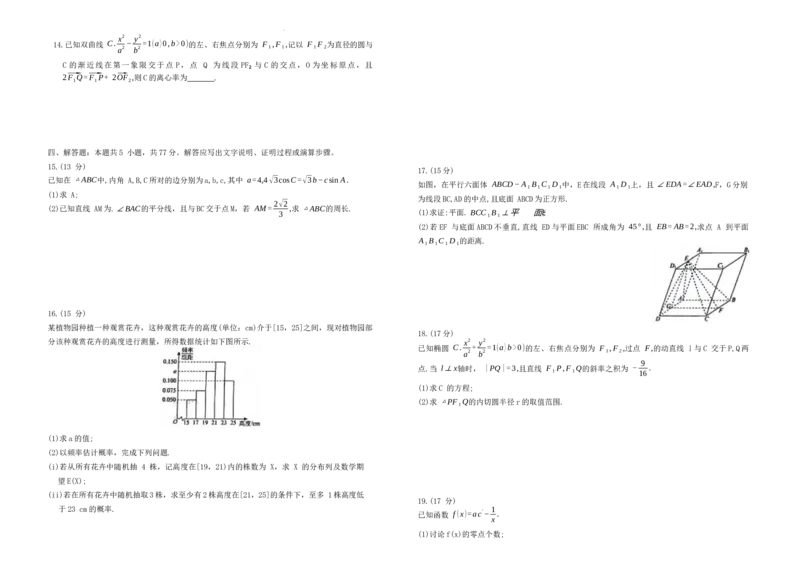
16.(15 分)
某植物园种植一种观赏花卉,这种观赏花卉的高度(单位:cm)介于[15,25]之间,现对植物园部
18.(17分)
分该种观赏花卉的高度进行测量,所得数据统计如下图所示. x2 y2
已知椭圆 C. + =1(a⟩b>0)的左、右焦点分别为 F₁,F₂,过点 F,的动直线 l与C 交于P,Q两
a2 b2
9
点.当 l⊥x轴时, |PQ|=3,且直线 F₁P,F₁Q的斜率之积为 − .
16
(1)求C 的方程;
(2)求 △PF₁Q的内切圆半径r的取值范围.
(1)求a的值;
(2)以频率估计概率,完成下列问题.
(i)若从所有花卉中随机抽 4 株,记高度在[19,21)内的株数为 X,求 X 的分布列及数学期
望E(X);
(ii)若在所有花卉中随机抽取3株,求至少有2株高度在[21,25]的条件下,至多 1株高度低
19.(17 分)
于23 cm的概率. 1
已知函数 f (x)=ac'− .
x
(1)讨论f(x)的零点个数;
学科网(北京)股份有限公司(2)当a>0时,| f (x)|>1+lnx,,求a的取值范围.
学科网(北京)股份有限公司