文档内容
高三年级考试
数学试题
2024.11
注意事项:
1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,
用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上
无效.
3.考试结束后,将本试卷和答题卡一并交回.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
1. 已知集合 , ,则( )
.
A B. C. D.
【答案】A
【解析】
【分析】根据集合的补集的定义即可求得.
【详解】因为 ,则 ,因为 ,则
, .
故选:A
2. 命题 的否定为( )
A. B.
C. D.
【答案】B
【解析】
第1页/共23页
学科网(北京)股份有限公司【分析】根据命题的否定的定义即可求解.
的
【详解】命题 否定为 .
故选:B.
3. 已知 , , ,且 ,则 ( )
A. 5 B. 6 C. 7 D. 12
【答案】D
【解析】
【分析】将对数式转化为指数式,结合指数运算,求解即可.
【详解】 ,故可得 ,又 ,则 .
故选:D.
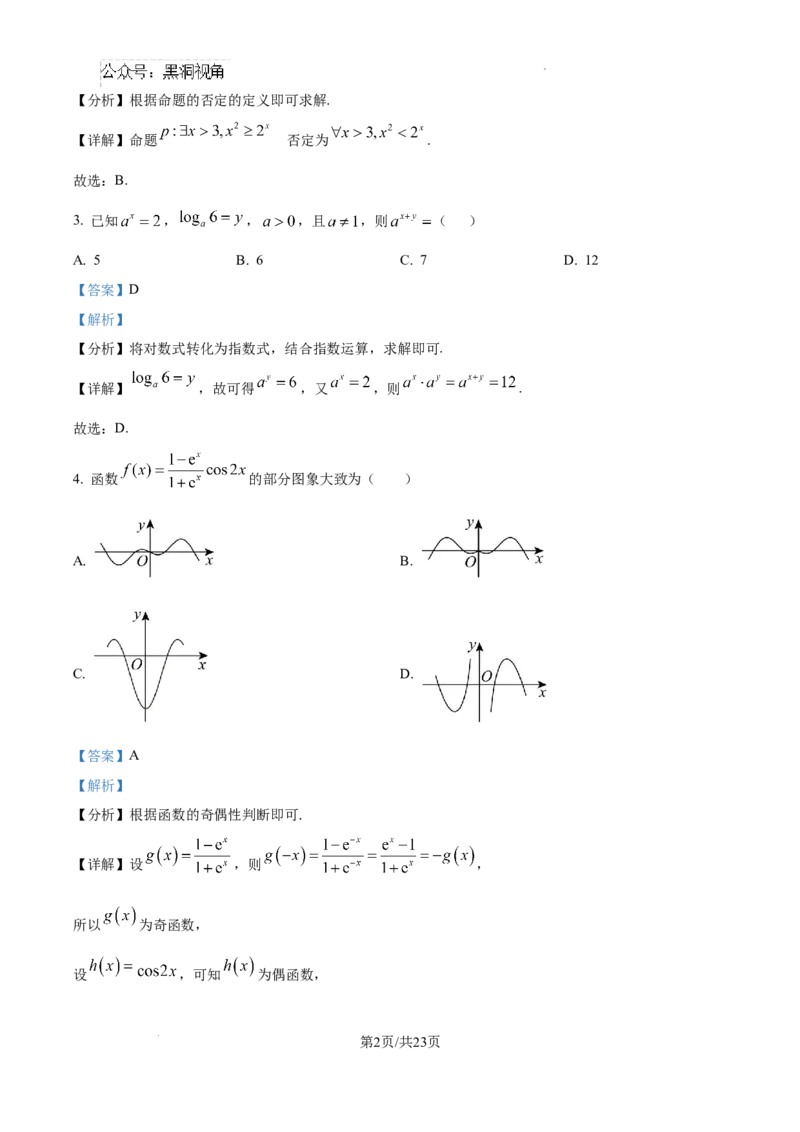
4. 函数 的部分图象大致为( )
A. B.
C. D.
【答案】A
【解析】
【分析】根据函数的奇偶性判断即可.
【详解】设 ,则 ,
所以 为奇函数,
设 ,可知 为偶函数,
第2页/共23页
学科网(北京)股份有限公司所以 为奇函数,则B,C错误,
易知 ,所以A正确,D错误.
故选:A.
5. 已知等差数列 的前n项和为 , , ,则 ( )
A. 220 B. 240 C. 260 D. 280
【答案】D
【解析】
【分析】根据等差数列的定义求得首项和公差,代入求和公式即可求得.
【详解】由数列 为等差数列,且 , ,则
,解得 , .
故选:D
6. 已知 ,则 ( )
A. B. C. D.
【答案】B
【解析】
【分析】根据已知条件即可求得 ,代入即可求得.
【详解】由 ,则
,化简得 ,所以
第3页/共23页
学科网(北京)股份有限公司,由 .
故选:B
7. “函数 的图象关于 对称”是“ , ”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 即不充分也不必要条件
【答案】B
【解析】
【分析】利用充分条件和必要条件的定义判断.
【详解】解:当 , 时, ,
令 ,解得 ,则函数的对称中心为 ,故必要;
当 的图象关于 对称时,令 ,解得 ,故不充
分,
故选:B
8. 已知 对任意 恒成立,则 的解集为(
)
A. B.
C. D.
【答案】C
【解析】
【分析】分析条件可知 的解集为 ,得到 和 的关系,不等式等价转
第4页/共23页
学科网(北京)股份有限公司化后可得不等式的解集.
【详解】由 得, .
当 得, , ,
当 得, , ,
当 得, , .
∵ 对任意 恒成立,
∴由 得, ,
∴ 和 是方程 的两根,且 ,
∴ ,故 .
由 得, ,即 ,
解得 ,故不等式的解集为 .
故选:C.
【点睛】思路点睛:本题考查一元二次不等式综合问题,具体思路如下:
(1)分析 在不同定义域上的取值范围,可得到 的解集为 .
的
(2)根据不等式 解集结合韦达定理可得 , .
(3) 可转化为 ,解不等式可得结果.
第5页/共23页
学科网(北京)股份有限公司二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合
题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9. 已知a,b, ,则下列命题正确的是( )
A. 若 ,则 B. 若 ,则
C. 若 ,则 D. 若 ,则
【答案】BC
【解析】
【分析】由不等式的基本性质即可判定各个选项.
【详解】A选项:当 , 时, ,但 ,故A错误;
B选项:∵ ,∴当 时, ,故B正确;
C选项:∵ ,∴ , ,由∵ ,
∴ ,故C正确;
D选项: ,则 ,当 时, ,故D错误.
故选:BC.
10. 已知函数 ,则下列选项正确的是( )
A.
B. 将函数 的图象向右平移 个单位长度,得到的函数图象关于原点对称
第6页/共23页
学科网(北京)股份有限公司C. 是函数 的极大值点
D. 当 时,函数 的值域为
【答案】BCD
【解析】
【分析】计算 可得选项A错误;计算平移之后的函数表达式,得到奇函数,选项 B正确;分析
函数在 上为增函数,在 上为减函数,可得选项C正确;分析函数在 的单调性,计算
最值,可得选项D正确.
【详解】A.由 得,
,
∴ ,选项A错误.
B.由题意得, ,
函数 的图象向右平移 个单位长度得,
,
得 为奇函数,函数图象关于原点对称,选项B正确.
C.由 得, ,
第7页/共23页
学科网(北京)股份有限公司当 时, , , ,
当 时, , , ,
∴ 在 上为增函数,在 上为减函数, 是函数 的极大值点,选项C正确.
D. 由 可知,
当 时, , , ,
结合选项C可得, 在 上为增函数,在 上为减函数,在 上为增函数.
∵ , ,
, ,
∴ , ,
故函数 的值域为 ,选项D正确.
故选:BCD.
11. 已知各项均为正数的数列 的前n项和 , , ,则下列选项正确的
是( )
A. B. 数列 是递减数列
C. D. , ,
第8页/共23页
学科网(北京)股份有限公司【答案】BCD
【解析】
【分析】先令 ,得到 ,判断选项A;然后当 时,得 ,消除前 项和,得到
相邻两项的关系,借此来判断选项BC;最后,利用前面得到的 的范围建立不等式,放缩求解,判断选
项D.
【详解】令 ,得 ,因为 ,
所以 ,故A错误;
当 时,得
所以
所以
得
由题可知,
故 与 同号
因为
所以 ,故C正确;
因为 ,所以
得 ,所以 是递减数列,故B正确;
第9页/共23页
学科网(北京)股份有限公司因为 , ,所以
所以
得
所以当 时, ,
所以 ,
所以 ,
故选项D正确.
故选:BCD
【点睛】关键点点睛:因为数列 是一个递减数列,所以每一项都小于2,然后累加得到 ,然后
根据题中等式得到 ,然后再因为 ,利用列项相消的方式求和即可.
三、填空题:本题共3小题,每小题5分,共15分.
12. 函数 的定义域为__________.
【答案】
【解析】
【分析】根据分式的分母不为 ,对数的真数大于 求解即可.
【详解】 ,
第10页/共23页
学科网(北京)股份有限公司解得 且 ,
函数 的定义域为 .
故答案为: .
13. 已知数列 满足 ,设 的前n项和为 ,若 ,则 __________.
【答案】123
【解析】
【分析】由递推公式得到数列前6项的值,通过观察发现数列规律,从而求得前50项的和.
【详解】由题意可知: , , , ,
, ,……
由此可得 是一个周期为4的周期数列
∴ .
故答案为:123.
14. 已知函数 ,若存在 ,使得 ,则实数
的取值范围是__________.
【答案】
【解析】
【分析】对 , 及 进行分类讨论,分别判断条件是否满足,即可得到答案.
【详解】设 ,则 , .
第11页/共23页
学科网(北京)股份有限公司2t2−t−2
故对 有ℎ ′′(t)=− >0,对 有 .
t2
这表明 在 上递增,在 上递减.
而 ,
ℎ
′(1+√17)
=ln
1+√17
+1−2⋅
√17−1
−2⋅
1+√17
+3=ln
1+√17
+4−√17>0,
4 4 4 4 4
.
所以结合 单调性知,存在 ,使得对 有 ,对
的
有 ,且 .
这表明 在(0,1)和 上递减,在 上递增.
从而对 有 ,对 有 ,对 有 .
故对任意 ,都有 ,而对任意 ,都有 .
下面对 进行分类讨论:
|a2−4a| |a2−4a| a2−4a
①若 ,则对x> +e有 ,x> ≥ ,从而
−2a −2a −2a
,且 .
故f (x)=(2−a)xlnx−2ax2−(a2−4a)x≥(2−a)xlnx≥2xlnx≥2>1,满足条件;
②若 ,则有
第12页/共23页
学科网(北京)股份有限公司,满足条件;
③若 ,设 ,则
.
1
从而对
有g′(x)=− (2x+1)(ax−1)>0,对
有 .
x2
所以 在 上递增,在 上递减,这就得到
.
故对任意 ,都有
,不满足条
件.
综上, 的取值范围是 .
故答案为:
【点睛】关键点点睛:本题的关键在于分类讨论,以求得 的取值范围.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15. 已知函数 ,其中 , .
第13页/共23页
学科网(北京)股份有限公司(1)若 , 的最小正周期为 ,求 的单调递增区间;
(2)若函数 的部分图象如图所示,其中 , ,求 的解析式.
【答案】(1) .
(2)
【解析】
【分析】(1)由周期公式确定函数解析式,再由整体代换即可求解;
(2)由 两点可确定周期,再结合 可得 即可求解.
【小问1详解】
因为函数 , , 的最小正周期为 ,
所以 ,解得: ,又 ,
所以 ,
由 ,
解得: ,
所以 的单调递增区间为: .
【小问2详解】
由 , ,
第14页/共23页
学科网(北京)股份有限公司可得 ,即 ,得:
同时 ,结合 ,
可得: ,
所以
16. 已知函数 .
(1)求函数 的单调区间;
(2)讨论方程 ( )解的个数.
【答案】(1) 的单调递减区间是 ,单调递增区间是 .
(2)详见解析.
【解析】
【分析】(1)根据函数的导函数与函数的单调性的关系可得函数单调区间;
(2)由(1)得到函数的单调区间,从而求出函数的极大值和极小值,由此讨论出 在对应取值范围内方
程 解的个数.
【小问1详解】
的定义域为 ,
,
由f′(x)<0,可得 ,由 ,可得 或x>0,
∴函数 的单调递减区间是 ,单调递增区间是 .
【小问2详解】
第15页/共23页
学科网(北京)股份有限公司由(1)可知函数 在 ,(0,+∞)上单调递增;函数 在 上单调递减,
∴ 在 时函数取极大值: ; 在 时函数取极小值: ,
又∵ , ,∴ ,
可得函数的大致图象,
∴当 时, 有0个解;
当 或 时, 有1个解;
当 时, 有3个解;
当 时, 有2个解.
17. 在 中,内角 A,B,C 所对的边分别为 a,b,c,A 为锐角, 的面积为 S,且
.
(1)求A;
(2)若 ,求S的最大值.
【答案】(1)
(2)
第16页/共23页
学科网(北京)股份有限公司【解析】
【分析】(1)通过二倍角公式与余弦定理化简原式,即可求得;
的
(2)借助余弦定理和基本不等式可以求得面积 最大值.
【小问1详解】
由 得,
,
化简得, ,又根据余弦定理
,则代入上式可得 即 ,
因为A为锐角,所以 .
【小问2详解】
,由 ,
,则 , ,
所以S的最大值为 .
18. 已知函数 .
(1)若 , 是定义在 上的函数, , .证明:
当 时, 为周期函数.
第17页/共23页
学科网(北京)股份有限公司(2)若曲线 在 处的切线方程为 ,设 (
), 为 的导函数,且 有两个极值点 , ( ).证明:.
【答案】(1)证明见解析
(2)证明见解析
【解析】
【分析】(1)首先根据偶函数的判定得 为偶函数,再计算得 ,则证明其为周期函数;
(2)直接求导,根据 得到 值,则得到 的解析式,两次求导得到再结合韦达
定理得到 ,作差化简得 ,将
原不等式转化为证明 ,再设新函数求导即可.
【小问1详解】
时, ,
,则
,
为偶函数.
第18页/共23页
学科网(北京)股份有限公司① , ,
② , ;
③ , .
, 为偶函数.
, ,
, ,
即 为周期函数.
【小问2详解】
由题意得 ,
由已知, , ,
, ,
,
设
.
由已知, 为 在 上的两个不等实根,且 ,
, .
第19页/共23页
学科网(北京)股份有限公司,
,
要证: ,
只需证 ,
即证 .
设 ,则 ,
在 上单调递减,又 .
.
,
原不等式成立.
【点睛】关键点点睛:本题第二问的关键是首先求出 值,从而得到 的表达式,再多次求导得到韦
达定理式,最后再对要证明的不等式进行等价转化,减少变量,最后重新设函数利用导数证明即可.
19. 数学归纳法是一种数学证明方法,通常被用于证明某个给定的命题在整个(或者局部)自然数范围内
成立,证明分为下面两个步骤:1.证明当 ( )时命题成立;2.假设 ( ,且
)时命题成立,推导出在 时命题也成立.只要完成这两个步骤,就可以断定命题对从 开始的所
第20页/共23页
学科网(北京)股份有限公司有自然数 n 都成立.已知有穷递增数列 , , , 且 .定义:集合
, 若 对 , , 使 得
,则称 具有性质T.
(1)若数列 ,1,2,m( )具有性质T,求实数m的值;
(2)若 具有性质T,且 , ,
(ⅰ)猜想当 时 的通项公式,并用数学归纳法证明你的猜想;
(ⅱ)求 ( ).
【答案】(1)4; (2)(ⅰ) ;(ⅱ) .
【解析】
【分析】(1)讨论 的不同取法,根据性质 的定义,结合数列的单调性,即可求得参数值;
(2)(ⅰ)猜想 ,再利用数学归纳法,结合性质 的定义,分类讨论,即可证明;
(ⅱ)利用(ⅰ)中所求通项公式,利用裂项求和法,即可求得结果.
【小问1详解】
由已知,数列 具有性质 ,
当 时,取 ,满足题意;
当 时,取 ,满足题意;
当 时, ,此时 中有且仅有一个数为 ,
若 ,则 ,不满足题意;
第21页/共23页
学科网(北京)股份有限公司若 ,则 或 或 ,
又因为 ,故 ;
综上所述, .
【小问2详解】
(ⅰ)猜想 .
当 时, 满足题意;
假设 时, 成立,则当 时,
若 ,则取 满足题意;
若 ,则 中有且仅有一个数为 ,
当 时,设 ,则 ,
故 ,当且仅当 时,取得等号;
当 时,设 ,则 ,
记 ,则 ;
因为对任意的 ,都有 在 中取到,
则 ,即 ;
故 ,故 成立;
综上, .
(ⅱ)因为 时,
第22页/共23页
学科网(北京)股份有限公司故
.
【点睛】关键点点睛:解决本题第二问的关键,一是,能够数量掌握数学归纳法的证明过程;二是,能够
根据性质 的定义,合理的分类讨论;三是,数量掌握裂项求和法求解数列的前 项和.
第23页/共23页
学科网(北京)股份有限公司