文档内容
密★启用前
东莞实验中学 2024-2025 学年第二学期第一次段考
高二数学
2025.3.24
一、单项选择题:本大题共 8小题,每小题 5分,共 40分. 在每小题给出的四个选项
中,只有一项是符合题目要求的. 请把正确选项在答题卡中的相应位置涂黑.
1.(sin2x) ′=( )
A.2sinxcosx B.−2cos2x C.2cos2x D.2
2.从4名男同学、3名女同学中选3名同学组成一支志愿者小队,要求男、女都有,则
不同的组队方案共有( )
A.60种 B.50种 C.40种 D.30种
3.日常饮用水通常都是经过净化的,随着水纯净度的提高,所需净化费用不断增加.已
4000
知1吨水净化到纯净度为x%时,所需费用(单位:元)为c(x)= (801,不等式
f (ax)≥f
(lnx2)恒成立,则正实数a的最小值为
e
D.若方程g(x)=t有两个解x ,x ,则x +x <2
1 2 1 2
三、填空题:本大题共3小题,每小题5分,共15分. 请把答案填在答题卡的相应位置
上.
12.若 ,则 .
C1 +C2 =15 m=
m m
π
( )
13.曲线f (x)=sinx−2cosx−1在点 ,0 处的切线方程为 .
2
14.用半径为R的圆形铁皮剪出一个圆心角为α的扇形,制成一个圆锥形容器.当该容器
的容积最大时,扇形的圆心角α= .
四、解答题: 本大题共5小题,第15题13分,第16、17题各15分,第18、19题各17
分,共77分.解答应写出文字说明、证明过程或演算步骤. 必须把解答过程写在答题卡
相应题号指定的区域内,超出指定区域的答案无效.
15.(本小题满分13分)
1
已知函数f(x)= x2−4x+3lnx.
2
(1)求f(x)的单调区间;
[1 )
(2)求f(x)在区间 ,e 上的最大值.
e16.(本小题满分15分)
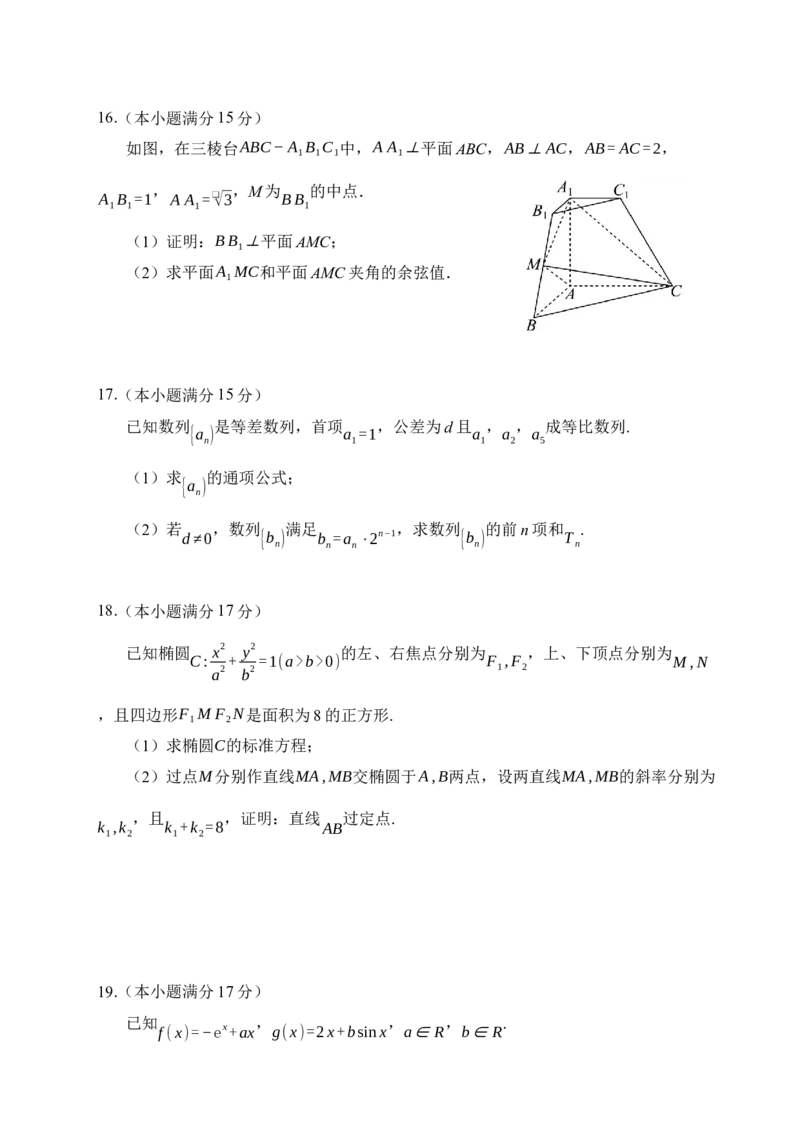
如图,在三棱台ABC−A B C 中,A A ⊥平面ABC,AB⊥AC,AB=AC=2,
1 1 1 1
, ,M为 的中点.
A B =1 A A =❑√3 BB
1 1 1 1
(1)证明:BB ⊥平面AMC;
1
(2)求平面A MC和平面AMC夹角的余弦值.
1
17.(本小题满分15分)
已知数列 是等差数列,首项 ,公差为d且 , , 成等比数列.
{a ) a =1 a a a
n 1 1 2 5
(1)求 的通项公式;
{a )
n
(2)若 ,数列 满足 ,求数列 的前n项和 .
d≠0 {b ) b =a ⋅2n−1 {b ) T
n n n n n
18.(本小题满分17分)
已知椭圆 x2 y2 的左、右焦点分别为 ,上、下顶点分别为
C: + =1(a>b>0) F ,F M,N
a2 b2 1 2
,且四边形F M F N是面积为8的正方形.
1 2
(1)求椭圆C的标准方程;
(2)过点M分别作直线MA,MB交椭圆于A,B两点,设两直线MA,MB的斜率分别为
,且 ,证明:直线 过定点.
k ,k k +k =8 AB
1 2 1 2
19.(本小题满分17分)
已知 , , , .
f(x)=−ex+ax g(x)=2x+bsinx a∈R b∈R(1)讨论f(x)的单调性;
(2)若a=−1,曲线y=f(x)的任意一条切线,都存在曲线y=g(x)的某条切线与它垂
直,求实数b的取值范围.