文档内容
高三数学
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项
是符合题目要求的.
1.一个容量为 的样本,其数据依次为: 。则该组数据的第 百
分位数为( )
A. B. C. D.
2.记 为等差数列 的前 项和,若 ,则 ( )
A. B. C. D.
3.若 ,则 ( )
A. B. C. D.
4.直线 被圆 截得的最短弦的弦长为( )
A. B. C. D.
5.已知函数 在 上单调递增,则 的取值范围是( )
A. B. C. D.
6.已知四面体 内接于球 ,若 ,平面
平面 ,则球 的表面积是( )
A. B. C. D.
7.已知直线 与抛物线 相交于 两点,以 为直径的
圆与抛物线 的准线相切于点 ,则 ( )
A. B. C. D.
8.点 是 所在平面内的点,且有 ,直线 分别交
学科网(北京)股份有限公司于点 ,记 的面积分别为 ,则 ( )
A. B. C. D.
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题
目要求。全部选对的得6分,部分选对的得2分,有选错的得0分。
9.一口袋中有除颜色外完全相同的3个红球和2个白球,从中无放回的随机取两次,每次
取1个球,记事件A:第一次取出的是红球;事件A:第一次取出的是白球;事件B:取
1 2
出的两球同色;事件C:取出的两球中至少有一个红球,则( )
A. 事件 , 为互斥事件 B. 事件B,C为独立事件
C. D.
10.下列命题为真命题的是( )
A. 已知 是双曲线C的两个焦点,P为C上一点,且 ,则
双曲线C的离心率为
B. “ ”在 上恒成立的充要条件是“ ”
C. 已知函数 的定义域为 为奇函数, 为偶函数,则
D. 设 , , ,则 的大小关系为
11.已知函数 在区间 上单调,对 ,满
足 ,且 ,则下列说法正确的是( )
学科网(北京)股份有限公司A. 若函数 在区间 上单调,则
在 上恰存在 个极值点,则
B. 若函数
C. 函 数 在 上 有 四 个 零 点 , 则
, ,则
D. 若
三、填空题:本题共3小题,每小题5分,共15分.
12.已知复数 (其中 为虚数单位),
13.为进一步强化学校美育育人功能,构建德智体美劳全面培养的教育体系,某校开设了音
乐、美术、书法三门选修课程.该校某班级有5名同学分别选修其中一门课程学习,每门课程
至少有一位同学选修,则恰好有2位同学选修音乐的概率为
14.已知函数 在 上单调递增,则 的
最大值为
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
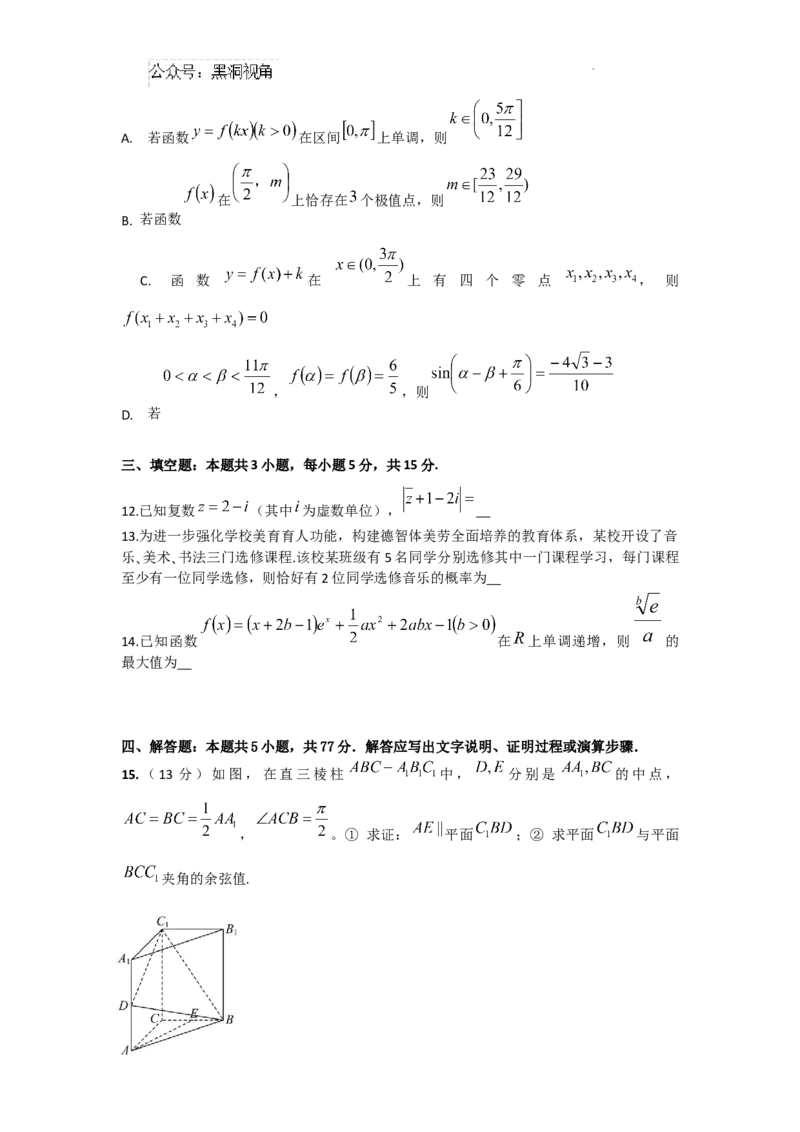
15.(13 分)如图,在直三棱柱 中, 分别是 的中点,
, 。① 求证: 平面 ;② 求平面 与平面
夹角的余弦值.
学科网(北京)股份有限公司16.(15分)在三角形 中,内角 的对边分别为 ,且 。
① 求 ;②若 ,且 ,求 的取值范围.
17.(15分)已知椭圆 的离心率为 ,过点 的直线
交椭圆 于点 ,且当 轴时, 。① 求椭圆 的方程;② 椭圆 的
左焦点为 ,若 的外心在 轴上,求直线 的方程.
18.(17分)已知函数 。① 当 ,求 的最大值;② 若
存在极大值,求实数 的取值范围.
19.(17分)对于一个给定的数列 ,令 ,则数列 称为数列 的一
阶和数列,再令 ,则数列 称为数列 的二阶和数列,以此类推,可得
数 列 的 阶 和 数 列 。 ① 数 列 的 二 阶 和 数 列 是 等 比 数 列 , 且
,求 ;② 若 ,求数列 的二阶和数列的前 项和;
③ 若数列 是首项为 的等差数列, 是数列 的一阶和数列,且 ,
,求正整数 的最大值,以及 取最大值时数列 的公差.
学科网(北京)股份有限公司学科网(北京)股份有限公司