文档内容
参考答案:
1-8:DBACBBCD
9. ACD 10.AC 11.ACD
12. 13. 14.
解答题
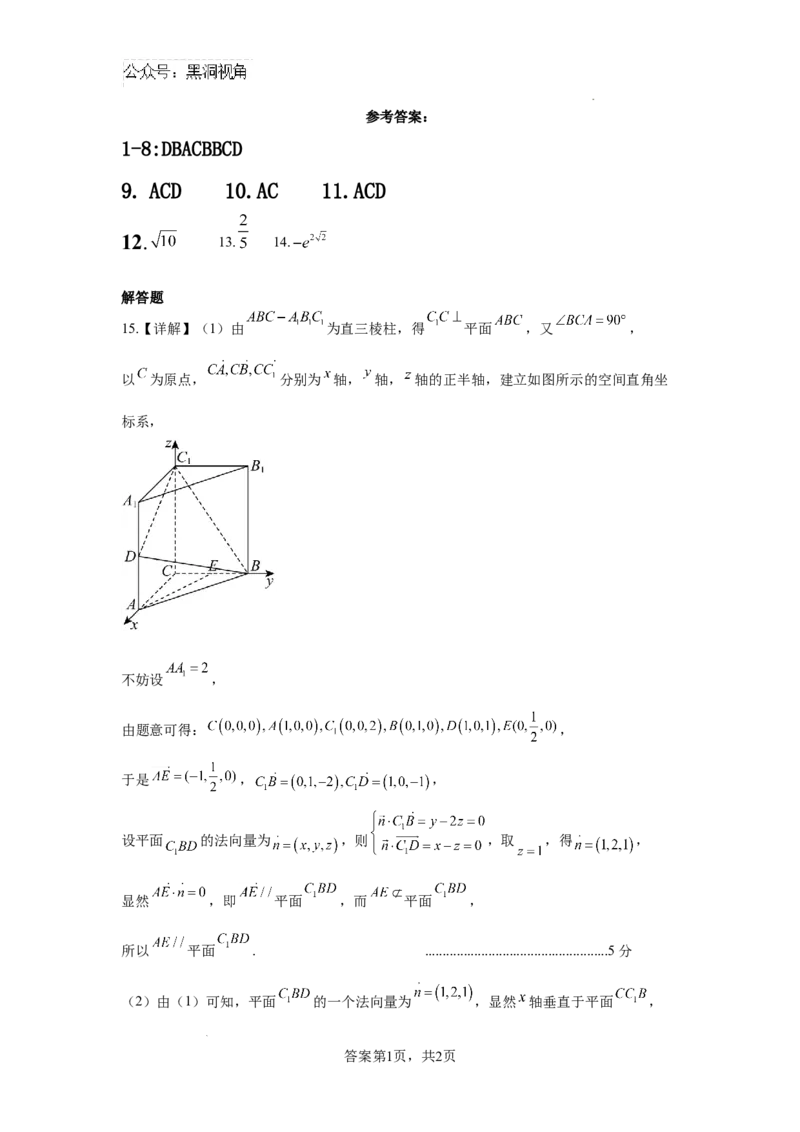
15.【详解】(1)由 为直三棱柱,得 平面 ,又 ,
以 为原点, 分别为 轴, 轴, 轴的正半轴,建立如图所示的空间直角坐
标系,
不妨设 ,
由题意可得: ,
于是 , ,
设平面 的法向量为 ,则 ,取 ,得 ,
显然 ,即 平面 ,而 平面 ,
所以 平面 . ....................................................5分
(2)由(1)可知,平面 的一个法向量为 ,显然 轴垂直于平面 ,
答案第1页,共2页
学科网(北京)股份有限公司不妨取其法向量为 ,设二面角 所对应的平面角为 ,
则 ,
显然二面角 为锐二面角,则 ,
即二面角 的余弦值为 .....................................................13分
16.(1) ....................................................6分
(2) ....................................................15分
17.【详解】(1)由题意得: ,得 ,
又当 时, ,则 ,所以 ,即 ,
所以椭圆 的方程为 . ....................................................6分
(2)设过 三点的圆的圆心为 ,A(x ,y ),B(x ,y ),又 ,
1 1 2 2
则 ,即 ,
又A(x ,y )在椭圆 上,故 ,代入上式化简得到: ,
1 1
①
答案第2页,共2页同理,根据 可以得到: ,②
由①②可得: 是方程 的两个根,则 ,设直线 : ,
联立方程: ,整理得: ,故 ,解得
,所以 ,所以直线 的方程为:
.....................................................15分
18.【详解】(1)由题可知 的定义域为(0,+∞),
当 时, , .
令 ,解得 .
当 时, , 单调递增;
当 时, , 单调递减.
所以当 时, 取极大值,也是最大值,故 的最大值为 ......................6
分
(2) .
令 ,则 .
答案第3页,共2页
学科网(北京)股份有限公司当 时, , 在(0,+∞)上单调递减,
当 时, ; ,根据零点存在定理,得 在(0,2)内存在
唯一的零点 ,
在 上,g(x)>0, , 单调递增;
在 上,g(x)<0, , 单调递减, 存在极大值.
当 时,令 ,解得 , (舍去),
在 上, , 单调递减;在 上, , 单调递增.
所以当 时, 取极小值,也是最小值,故 .
当 ,即 时,由于当 时, ,此时,在 上,
必定存在唯一的零点 .
在 上,g(x)>0, , 单调递增;在 ,g(x)<0, ,
单调递减, 存在极大值,
当 时在(0,+∞)上 , , 单调递增不存在极大值.
综上所述,a的取值范围是 . ...................................................17分
19.【详解】(1)由题意,得 , , ,
答案第4页,共2页所以 , ,
因为 是等比数列,所以公比为 ,由此得 , , ,
所以 , , ,
所以 , ,
..........................................4分
(2)设 的二阶和数列的前n项和为 ,
由题意,得 , ,
所以 ........................10分
(3)因为 ,
所以 ,解得 .
设数列 的公差为d,则 ,
得 ,
又因为 ,
所以 ,得 ,
所以k的最大值是1999,此时公差为 ......................................17分
答案第5页,共2页
学科网(北京)股份有限公司