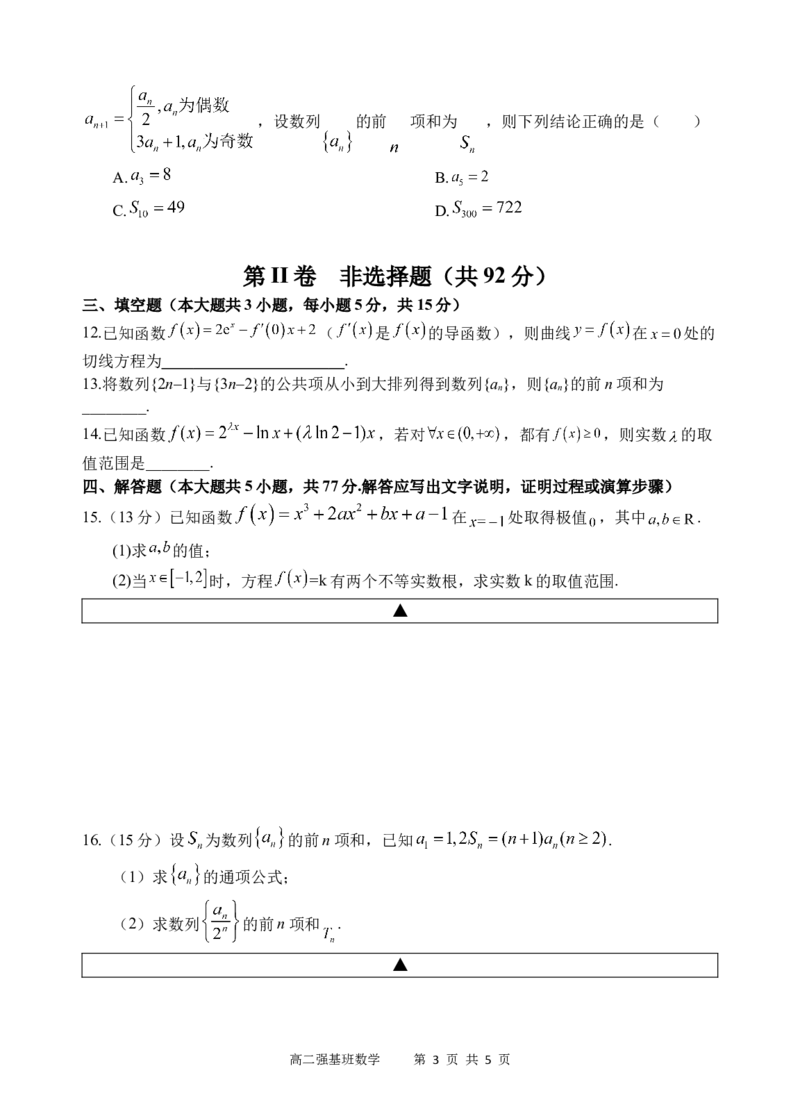文档内容
射洪中学高 2023 级高二(下)强基班第一次月考
数学试题
出题人:曹剑 审题人:郭海兵
(考试时间:120分钟 满分:150分)
注意事项:
1.答卷前,考生务必将自己的班级、姓名、考号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂
黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。写在本试卷上无效。
3.回答非选择题时,将答案写在答题卡对应题号的位置上。写在本试卷上无效。
4.考试结束后,将答题卡交回。
第 I 卷 选择题(共 58 分)
一、单选题(本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一
项是符合要求的)
1.已知 是定义在 上的可导函数,若 ,则 ( )
A. B. C.1 D.
2.若1,a,3成等差数列,1,b,4成等比数列,则 的值为( )
A. B. C.1 D.
3.已知函数 的导函数 的图象如图,则下列叙述正确的是
( )
A.函数 在 上单调递减
B.函数 在 处取得极小值
C.函数 只有一个极值点
D.函数 在 处取得极值
4.数列 的通项公式为 ,那么“ ”是“ 为递增数列”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
5.若函数 在 上为增函数,则 的取值范围为( )
A. B. C. D.
6.若直线 是指数函数 且 图象的一条切线,则底数 (
)
高二强基班数学 第 1 页 共 5 页A.2或 B. C. D. 或
7.设 和 分别表示正实数 的整数部分、小数部分,例如 .已知数列
满足 ,则 ( )
A. B.
C. D.
8.已知 是定义在 上的偶函数, 是 的导函数;当 时,
有 恒成立,且 ,则不等式 的解集是( )
A. B.
C. D.
二、多选题(本题共3小题,每小题6分,共18分,在每小题给出的四个选项中,有多项
符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分)
9.已知等差数列 的公差为 ,前 项和为 ,且 , 成等比数列,则(
)
A.
B.
C.当 时, 是 的最大值
D.当 时, 是 的最小值
10.已知函数 ,则下列结论正确的是( )
A. 是函数 定义域内的极小值点
B. 的单调减区间是
C.若 有两个不同的交点,则
D. 在定义域内既无最大值又无最小值
11.任取一个正整数,若是奇数,就将该数乘 再加上 ;若是偶数,就将该数除以 .反复进
行上述两种运算,经过有限次步骤后,必进入循环圈 .这就是数学史上著名
的“冰雹猜想”(又称“角谷猜想”).比如取正整数 ,根据上述运算法则得出
.猜想的递推关系如下:已知数列 满足 ,
高二强基班数学 第 2 页 共 5 页,设数列 的前 项和为 ,则下列结论正确的是( )
A. B.
C. D.
第 II 卷 非选择题(共 92 分)
三、填空题(本大题共3小题,每小题5分,共15分)
12.已知函数 ( 是 的导函数),则曲线 在 处的
切线方程为 .
13.将数列{2n–1}与{3n–2}的公共项从小到大排列得到数列{a },则{a }的前n项和为
n n
________.
14.已知函数 ,若对 ,都有 ,则实数 的取
值范围是________.
四、解答题(本大题共5小题,共77分.解答应写出文字说明,证明过程或演算步骤)
15.(13分)已知函数 在 处取得极值 ,其中 .
(1)求 的值;
(2)当 时,方程 =k有两个不等实数根,求实数k的取值范围.
▲
16.(15分)设 为数列 的前n项和,已知 .
(1)求 的通项公式;
(2)求数列 的前n项和 .
▲
高二强基班数学 第 3 页 共 5 页17.(15分)已知函数 .
(1)讨论函数 的单调性;
(2)当 时,记函数 的最小值为 ,求证: .
▲
18.(17分)已知数列 满足 , ( ).
(1)求证:数列 是等差数列,并求数列 的通项公式:
(2)记 , 为数列 的前n项和,若 对任意的正整数n都成立,
求实数 的取值范围.
▲
19.(17分)已知函数 .
(1)当 时,求 的极值;
高二强基班数学 第 4 页 共 5 页(2)若 有两个极值点 .
(i)求 的取值范围;
(ii)证明: .
▲
高二强基班数学 第 5 页 共 5 页