泸州市高2021级第一次教学质量诊断性考试理数(1)_2023年11月_0211月合集_2024届四川省泸州市第一次教学质量诊断性考试_四川省泸州市高2024届第一次教学质量诊断性考试理科数学

泸州市高 2021 级第一次教学质量诊断性考试 数 学 （理科） 本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，第Ⅰ卷 1至2页，第Ⅱ卷3至4页 共150分．考试时间 120分钟． 注意事项： 1．答题前，先将自己的姓名、准考证号填写在试卷和答题卡上，并将准考证号条形码粘贴在答 题卡上的指定位置． 2．选择题的作答：每小题选出答案后，用2B 铅笔把答题卡上对应题的答案标号涂黑． 3．填空题和解答题的作答：用签字笔直接答在答题卡上对应的答题区域内，作图题可先用铅笔 绘出，确认后再用 0.5毫米黑色签字笔描清楚，写在试题卷、草稿纸和答题卡上的非答题区域均 无效． 4．考试结束后，请将本试题卷和答题卡一并上交． 第Ⅰ卷（选择题 共60分） 一、选择题：本题共 12小题，每小题 5分，共60分．在每小题给出的四个选项中，只有一项 是符合题目要求的．  1   1 1  1．已知集合Ax xk ,kZ，B x x k ,kZ，则（ ）  2   2 2  A．B A B．A B C．A B D．AB  1 2．已知命题 p:xR，x2  2，命题q:x R ，lnx 2，则下列命题是真命题的为（ ） x2 0 0 A．(p)q B． pq C． p(q) D．(p)(q) 3．函数 y x的图象与函数 f(x)2x，g(x)log x，h(x) x3的图象交点的横坐标分别为a，b，c， 2 则（ ） A．abc B．bac C．cba D．acb 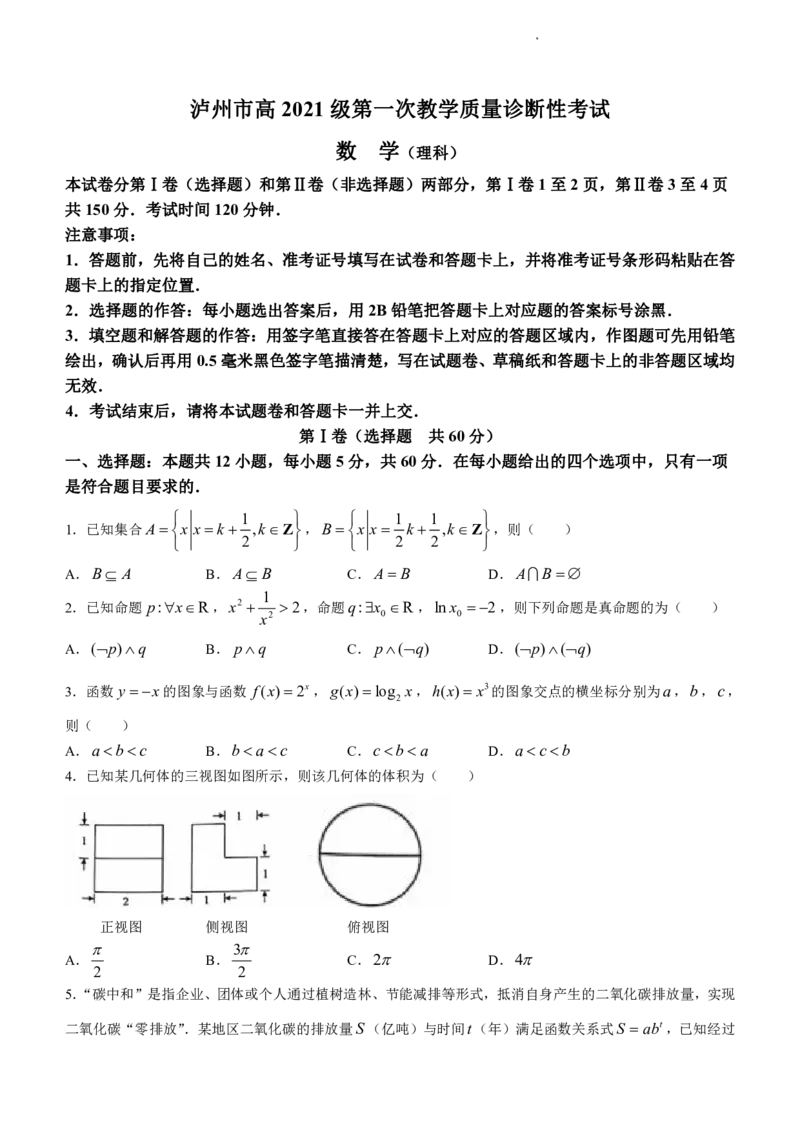4．已知某几何体的三视图如图所示，则该几何体的体积为（ ） 正视图 侧视图 俯视图  3 A． B． C．2 D．4 2 2 5．“碳中和”是指企业、团体或个人通过植树造林、节能减排等形式，抵消自身产生的二氧化碳排放量，实现 二氧化碳“零排放”．某地区二氧化碳的排放量S（亿吨）与时间t（年）满足函数关系式S abt，已知经过 学科网（北京）股份有限公司3a 4年，该地区二氧化碳的排放量为 （亿吨）．若该地区通过植树造林、节能减排等形式抵消自身产生的二氧 4 a 化碳排放量为 （亿吨），则该地区要实现“碳中和”，至少需要经过（ ）（参考数据：lg20.30，lg30.48） 3 A．13年 B．14年 C．15年 D．16年 6．“sin()0”是“tan tan”的（ ） A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 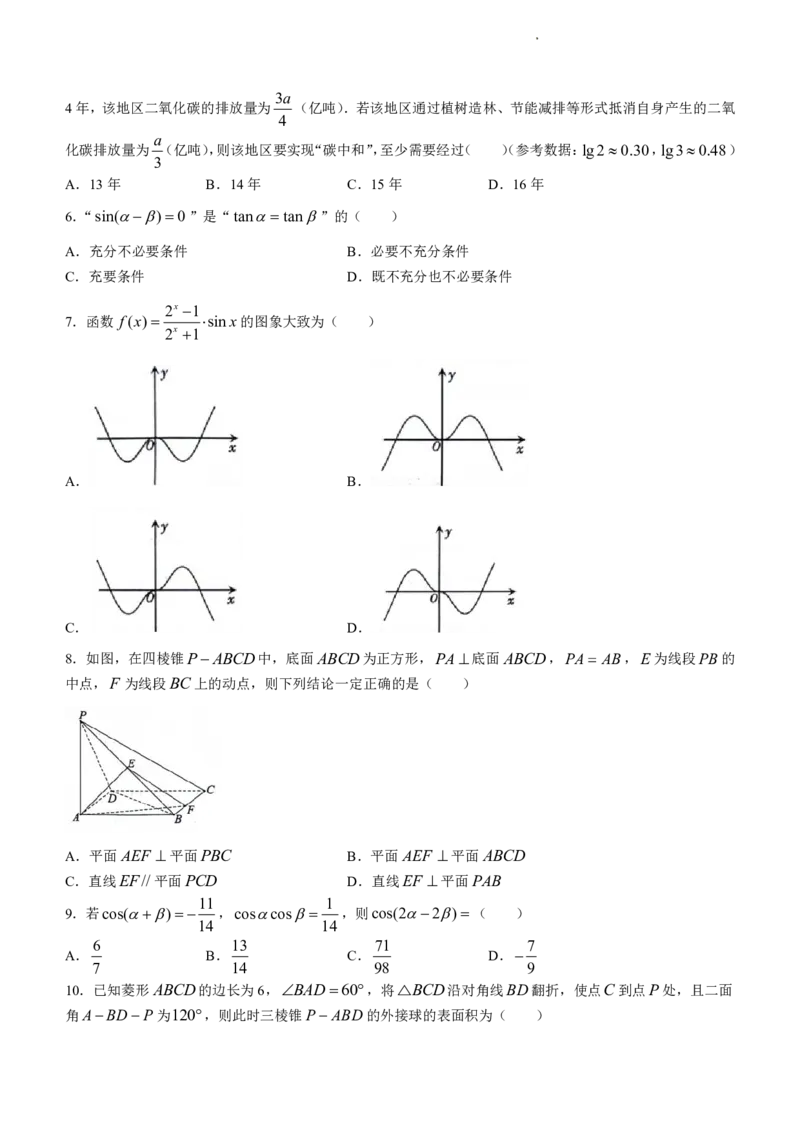2x 1 7．函数 f(x) sinx的图象大致为（ ） 2x 1 A． B． C． D． 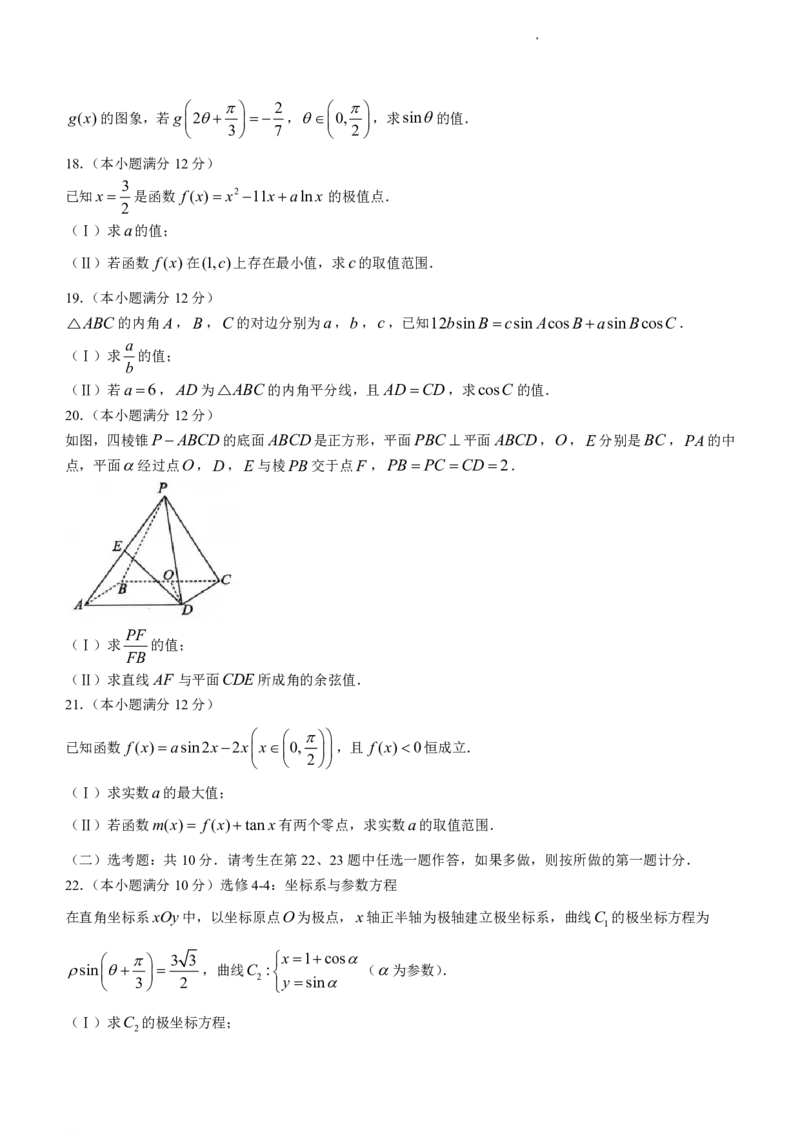8．如图，在四棱锥PABCD中，底面ABCD为正方形，PA底面ABCD，PA AB，E为线段PB的 中点，F 为线段BC上的动点，则下列结论一定正确的是（ ） A．平面AEF 平面PBC B．平面AEF 平面ABCD C．直线EF//平面PCD D．直线EF 平面PAB 11 1 9．若cos() ，coscos ，则cos(22)（ ） 14 14 6 13 71 7 A． B． C． D． 7 14 98 9 10．已知菱形ABCD的边长为6，BAD60，将△BCD沿对角线BD翻折，使点C到点P处，且二面 角ABDP为120，则此时三棱锥P ABD的外接球的表面积为（ ） 学科网（北京）股份有限公司A．21 B．28 21 C．52 D．84     2  11．已知函数 f(x)2sin x (0)在 0,  上存在最值，且在  ,  上单调，则的取值范围  6   3   3  是（ ）  2 11 17  5 5 8 A． 0,  B．  ,  C．  1,  D．  ,   3  4 3   3 2 3 12．已知定义在R上的奇函数 f(x)满足 f(x2) f(x)0，当x[0,1]时，f(x)2x 1，给出下列结论： （1）函数 f(x)的图象关于点(2,0)对称； （2）函数 f(x)的图象关于直线x3对称； （3）函数 f(x)在(1,3)上是增函数； （4） f(6) f(5.5) f(7)． 其中正确结论的个数为（ ） A．1 B．2 C．3 D．4 第Ⅱ卷（非选择题 共 90分） 注意事项： （1）非选择题的答案必须用 0.5毫米黑色签字笔直接答在答题卡上，作图题可先用铅笔绘出， 确认后再用0.5 毫米黑色签字笔描清楚，答在试题卷和草稿纸上无效． （2）本部分共 10个小题，共 90分． 二、填空题（本大题共4小题，每小题 5分，共 20分．把答案填在答题纸上）． 13．若函数 f(x)对一切实数x， y 都满足 f(x y) f(y)(x2y)x且 f(1)0，则 f(0)__________． 14．已知一个圆锥的体积为3，其侧面积是底面积的2倍，则其底面半径为__________． x2 15．函数 f(x) (x[0,1)(1,2])与函数y 2sinx1(0 x4)的图象的所有交点的横坐标与纵坐 x1 标之和等于__________． 1 16．过点(0,m)有两条直线与曲线 y  lnx相切，则实数m的取值范围是__________． x 三、解答题：共70分．解答应写出文字说明、证明过程或演算步骤．第 17~21题为必考题，每 个试题考生都必须作答．第 22、23题为选考题，考生根据要求作答． （一）必考题：共60分． 17．（本小题满分12分） 已知函数 f(x)2sin2x2 3sinxcosx1(0)的相邻两对称轴间的距离为． （Ⅰ）求函数 f(x)的解析式； 2 （Ⅱ）将函数 f(x)图象上点的横坐标伸长到原来的2倍，纵坐标不变，再向右平移 个单位长度得到函数 3 学科网（北京）股份有限公司  2   g(x)的图象，若g2   ， 0,  ，求sin的值．  3  7  2  18．（本小题满分12分） 3 已知x 是函数 f(x) x2 11xalnx 的极值点． 2 （Ⅰ）求a的值； （Ⅱ）若函数 f(x)在(1,c)上存在最小值，求c的取值范围． 19．（本小题满分12分） △ABC的内角A，B，C的对边分别为a，b，c，已知12bsinBcsinAcosBasinBcosC． a （Ⅰ）求 的值； b （Ⅱ）若a6，AD为△ABC的内角平分线，且ADCD，求cosC的值． 20．（本小题满分12分） 如图，四棱锥PABCD的底面ABCD是正方形，平面PBC 平面ABCD，O，E分别是BC，PA的中 点，平面经过点O，D，E与棱PB交于点F ，PBPC CD2． PF （Ⅰ）求 的值； FB （Ⅱ）求直线AF 与平面CDE所成角的余弦值． 21．（本小题满分12分）    已知函数 f(x)asin2x2xx 0,  ，且 f(x)0恒成立．   2 （Ⅰ）求实数a的最大值； （Ⅱ）若函数m(x) f(x)tanx有两个零点，求实数a的取值范围． （二）选考题：共10分．请考生在第22、23题中任选一题作答，如果多做，则按所做的第一题计分． 22．（本小题满分10分）选修4-4：坐标系与参数方程 在直角坐标系xOy中，以坐标原点O为极点，x轴正半轴为极轴建立极坐标系，曲线C 的极坐标方程为 1   3 3 x1cos sin    ，曲线C : （为参数）．  3 2 2 y sin （Ⅰ）求C 的极坐标方程； 2 学科网（北京）股份有限公司 （Ⅱ）已知点M(2,0)，曲线C 的极坐标方程为 ，C 与C 的交点为P，与C 的交点为O，Q，求 3 3 3 1 2 △MPQ的面积． 23．（本小题满分10分）选修4-5：不等式选讲 已知函数 f(x)|x||x2|1． （Ⅰ）求不等式 f(x)5的解集； a2 b2 1 （Ⅱ）若函数 f(x)的最小值为m，且abm（a0，b0）．求证：   ． a1 b1 3 学科网（北京）股份有限公司