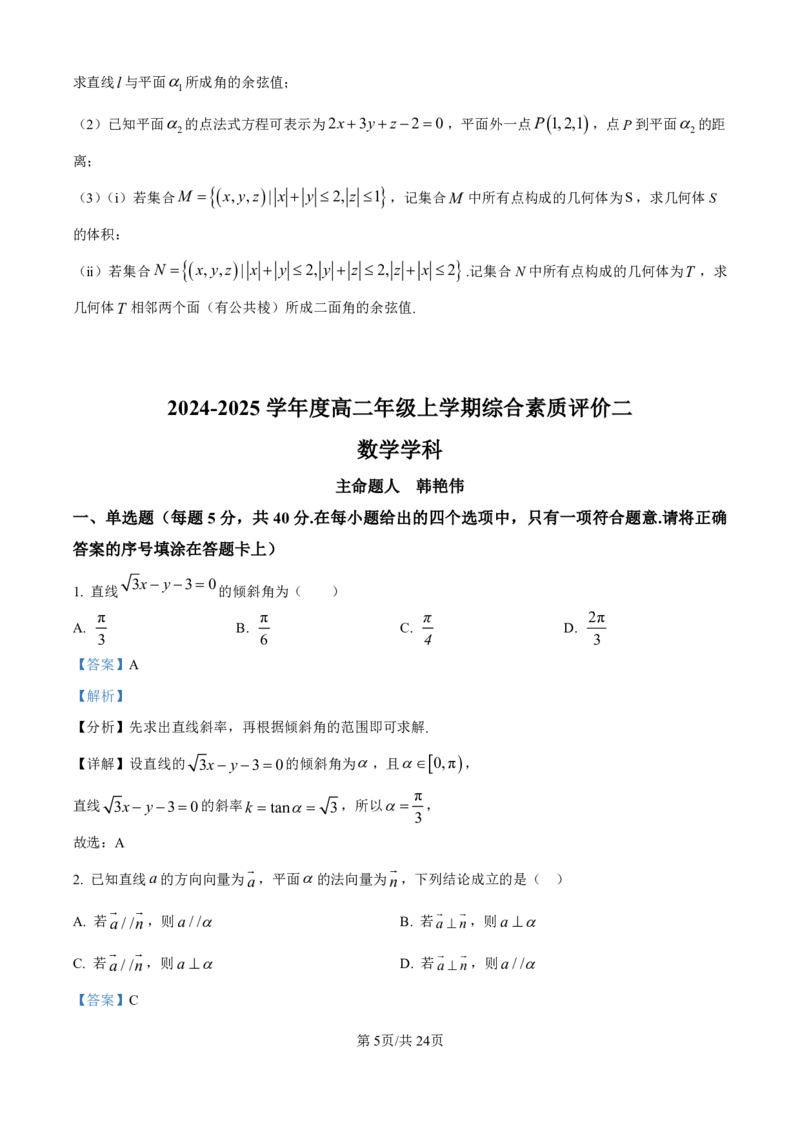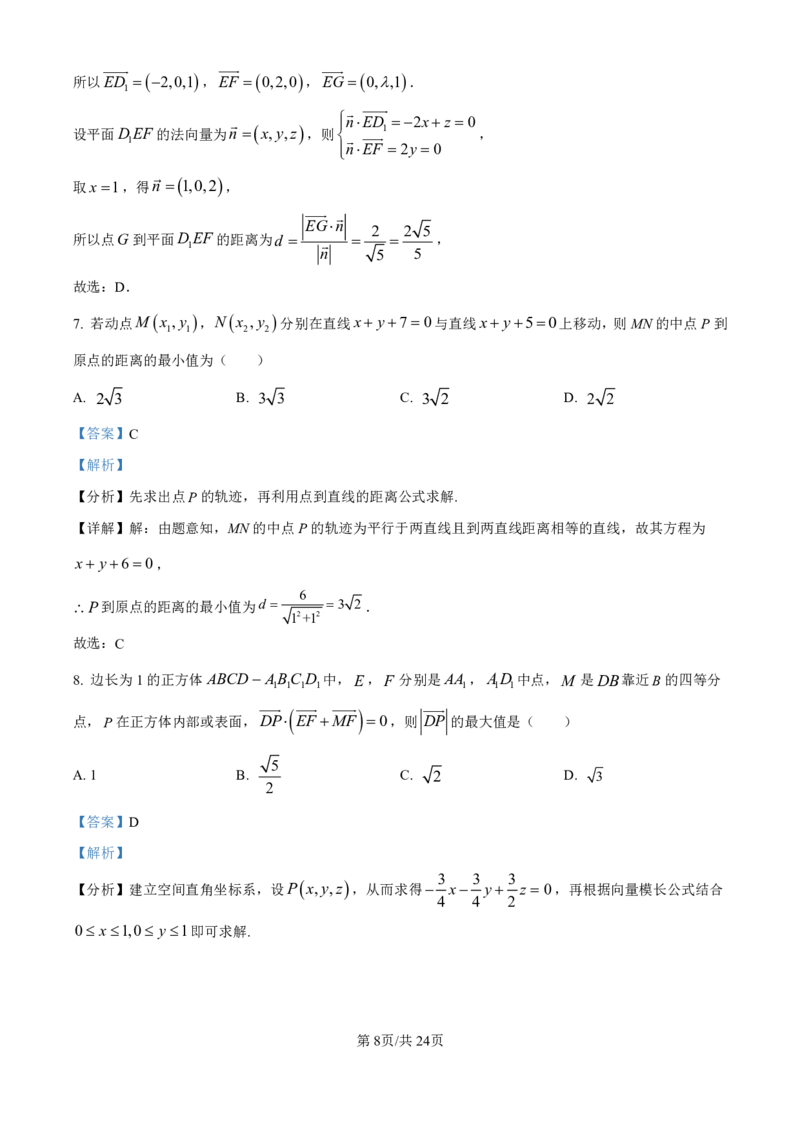数学-河北衡水中学2024-2025学年高二上学期综合素质评价_2024-2025高二（7-7月题库）_2024年11月试卷_1120河北衡水中学2024-2025学年高二上学期综合素质评价

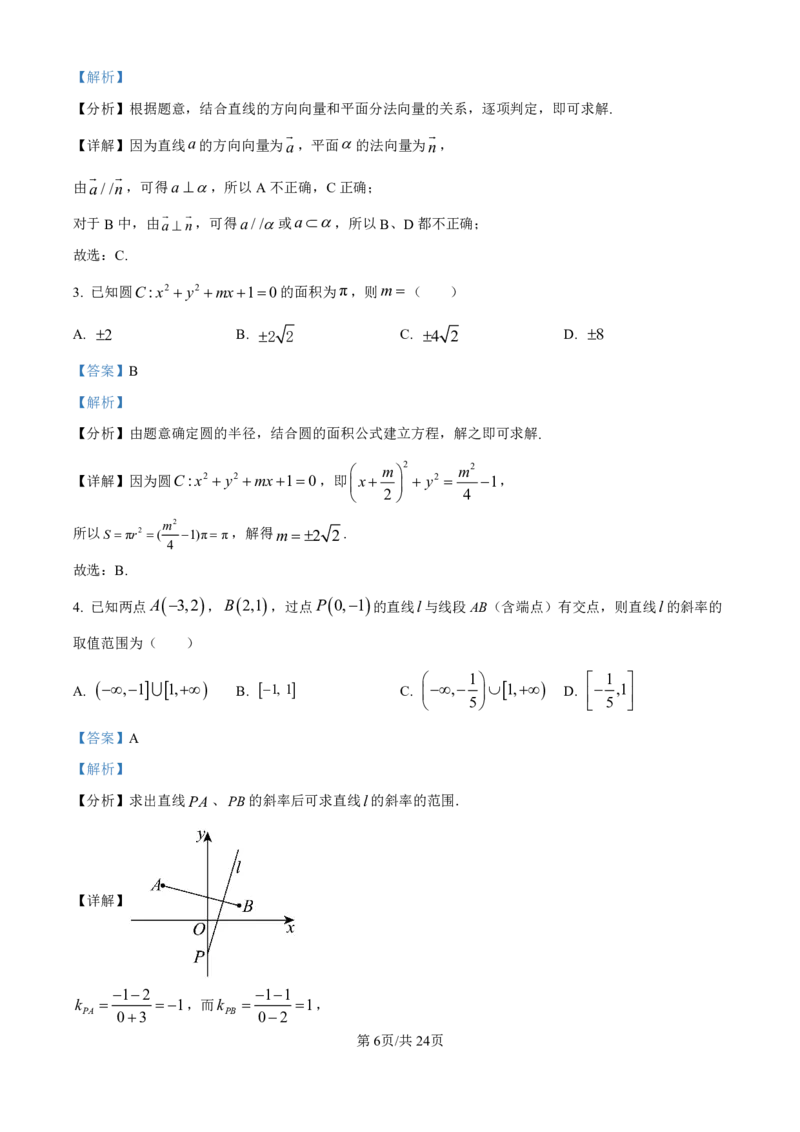
2024-2025 学年度高二年级上学期综合素质评价二 数学学科 主命题人 韩艳伟 一、单选题（每题 5 分，共 40 分.在每小题给出的四个选项中，只有一项符合题意.请将正确 答案的序号填涂在答题卡上） 3x y30 1. 直线 的倾斜角为（ ） π π π 2π A. B. C. D. 3 6 4 3   2. 已知直线a的方向向量为a，平面的法向量为n，下列结论成立的是（ ）     A. 若a//n，则a// B. 若an，则a      C. 若a//n，则a  D. 若an，则a// 3. 已知圆C:x2  y2 mx10的面积为π，则m（ ） A. 2 B. 2 2 C. 4 2 D. 8 4. 已知两点A 3,2  ，B  2,1  ，过点P  0,1  的直线l与线段AB（含端点）有交点，则直线l的斜率的 取值范围为（ ）  1  1  A . ,1    1, B. 1, 1 C.   , 5    1, D.    5 ,1   5. 已知A(0,1,1)，B(2,1,0)，C(3,5,7)，D(1,2,4)，则直线AB和直线CD所成角的余弦值为（ ） 5 22 5 22 2 22 2 22 A. B.  C. D.  66 66 33 33 6. 在棱长为2的正方体ABCDABC D 中，E，F 分别为棱AA ，BB 的中点，G为棱AB 上的一点， 1 1 1 1 1 1 1 1 且AG  02  ，则点G到平面DEF的距离为（ ） 1 1 3 2 2 2 5 A. B. 2 C. D. 3 3 5 7. 若动点M  x ,y  ，N  x ,y  分别在直线x y70与直线x y50上移动，则MN的中点P到 1 1 2 2 原点的距离的最小值为（ ） 第1页/共24页 学科网（北京）股份有限公司A 2 3 B. 3 3 C. 3 2 D. 2 2 . 8. 边长为1的正方体ABCDABC D 中，E，F 分别是AA ，AD 中点，M 是DB靠近B的四等分点， 1 1 1 1 1 1 1       P在正方体内部或表面，DP EF MF 0，则 DP 的最大值是（ ） 5 A.1 B. C. 2 D. 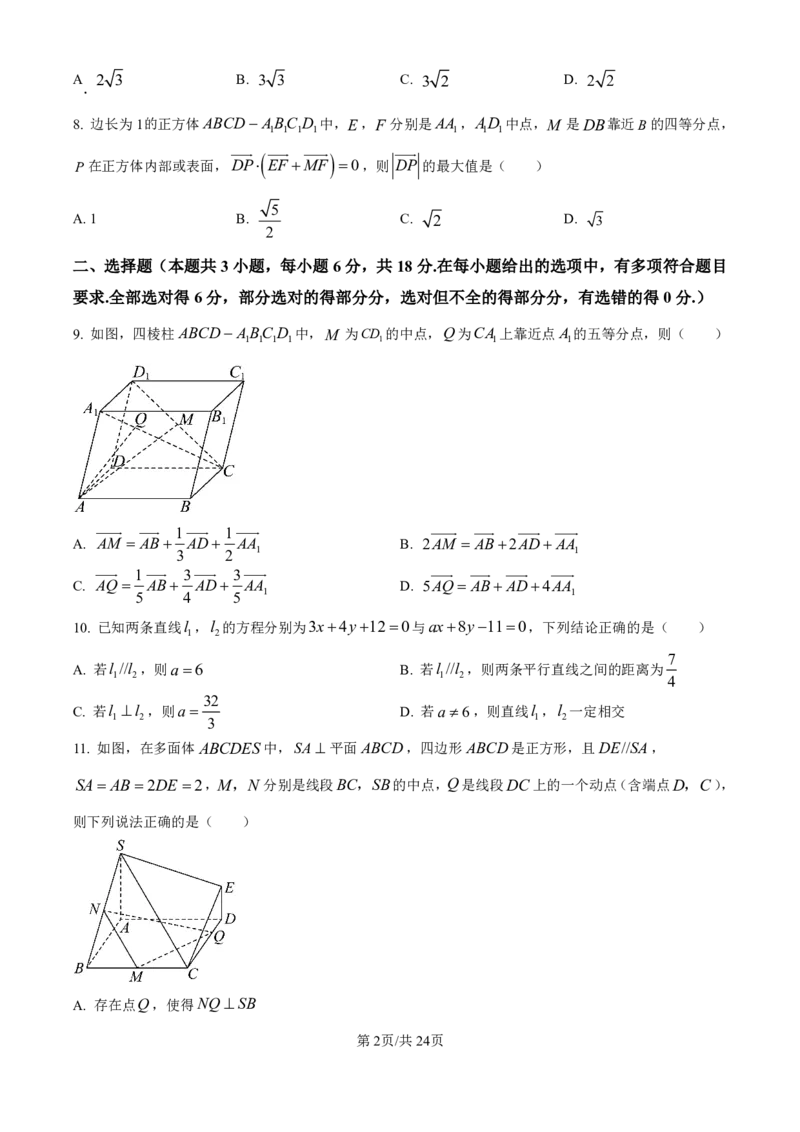3 2 二、选择题（本题共 3小题，每小题6 分，共 18分.在每小题给出的选项中，有多项符合题目 要求.全部选对得 6分，部分选对的得部分分，选对但不全的得部分分，有选错的得 0分.） 9. 如图，四棱柱ABCD ABC D 中，M 为CD 的中点，Q为CA 上靠近点A的五等分点，则（ ） 1 1 1 1 1 1 1   1 1     A. AM  AB AD AA B. 2AM  AB2ADAA 3 2 1 1  1 3 3     C. AQ  AB AD AA D. 5AQ  ABAD4AA 5 4 5 1 1 10. 已知两条直线l ，l 的方程分别为3x4y120与ax8y110，下列结论正确的是（ ） 1 2 7 A. 若l //l ，则a6 B. 若l //l ，则两条平行直线之间的距离为 1 2 1 2 4 32 C. 若l l ，则a  D. 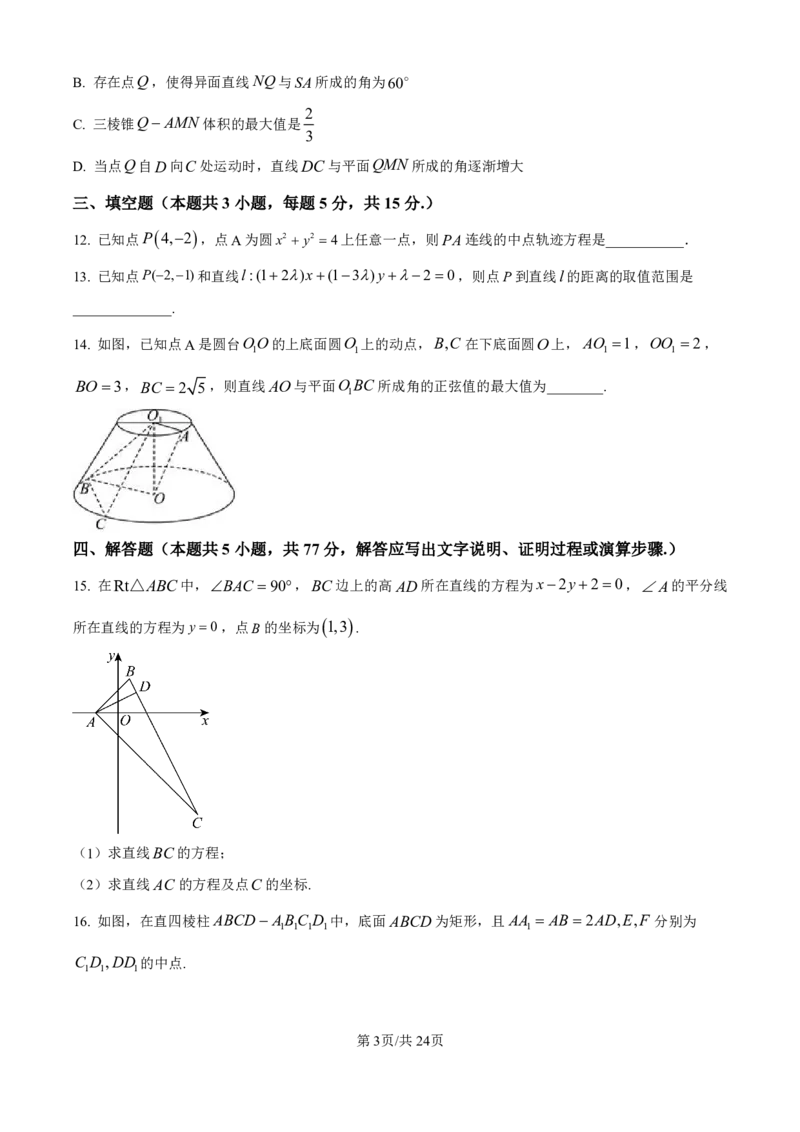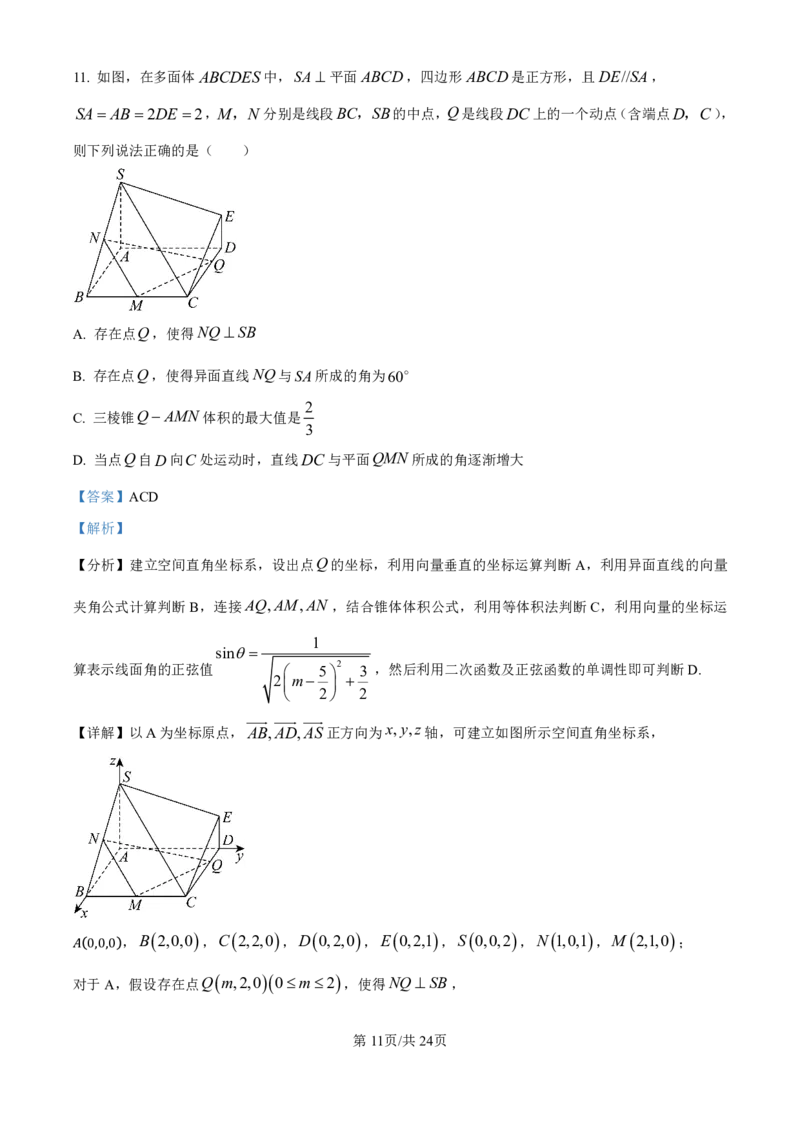若a 6，则直线l ，l 一定相交 1 2 1 2 3 11. 如图，在多面体ABCDES中，SA平面ABCD，四边形ABCD是正方形，且DE//SA， SA AB2DE 2，M，N 分别是线段BC，SB的中点，Q是线段DC上的一个动点（含端点D，C）， 则下列说法正确的是（ ） A. 存在点Q，使得NQSB 第2页/共24页 学科网（北京）股份有限公司B. 存在点Q，使得异面直线NQ与SA所成的角为60o 2 C. 三棱锥Q AMN 体积的最大值是 3 D. 当点Q自D向C处运动时，直线DC与平面QMN所成的角逐渐增大 三、填空题（本题共 3小题，每题 5分，共 15分.） 12. 已知点P  4,2  ，点A为圆x2  y2 4上任意一点，则PA连线的中点轨迹方程是___________． 13. 已知点P(2,1)和直线l:(12)x(13)y20，则点P到直线l的距离的取值范围是 ______________. 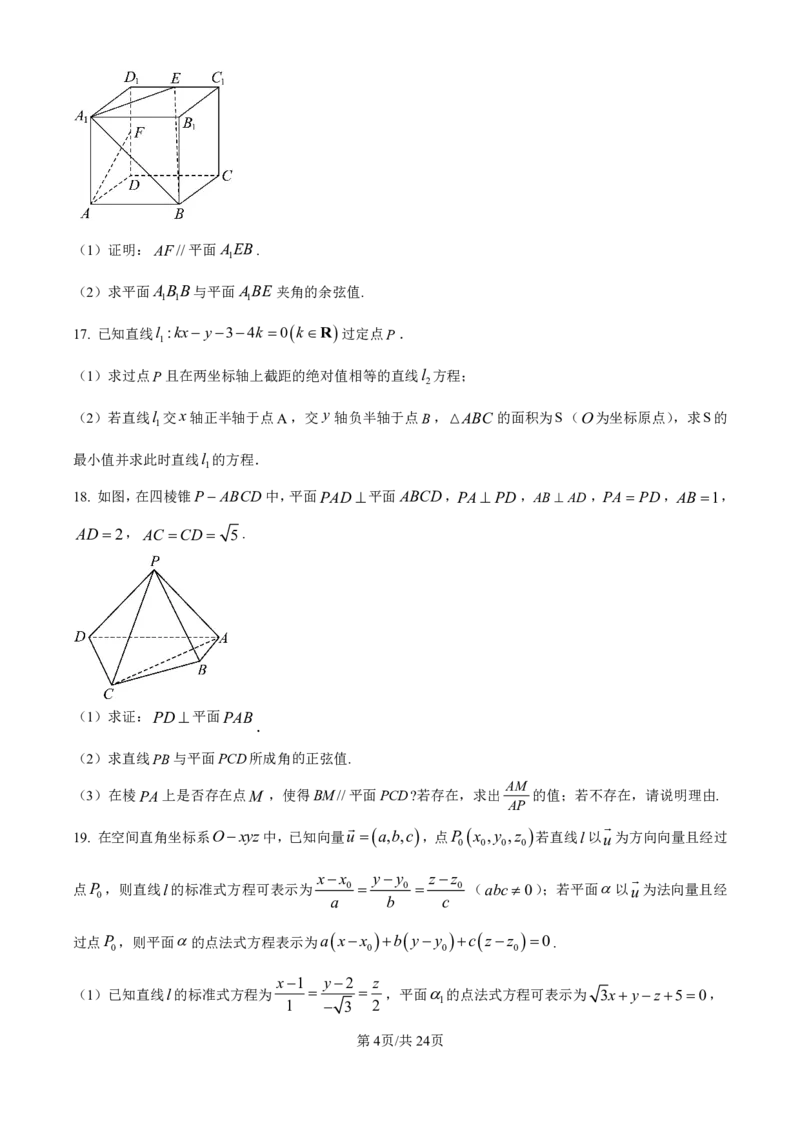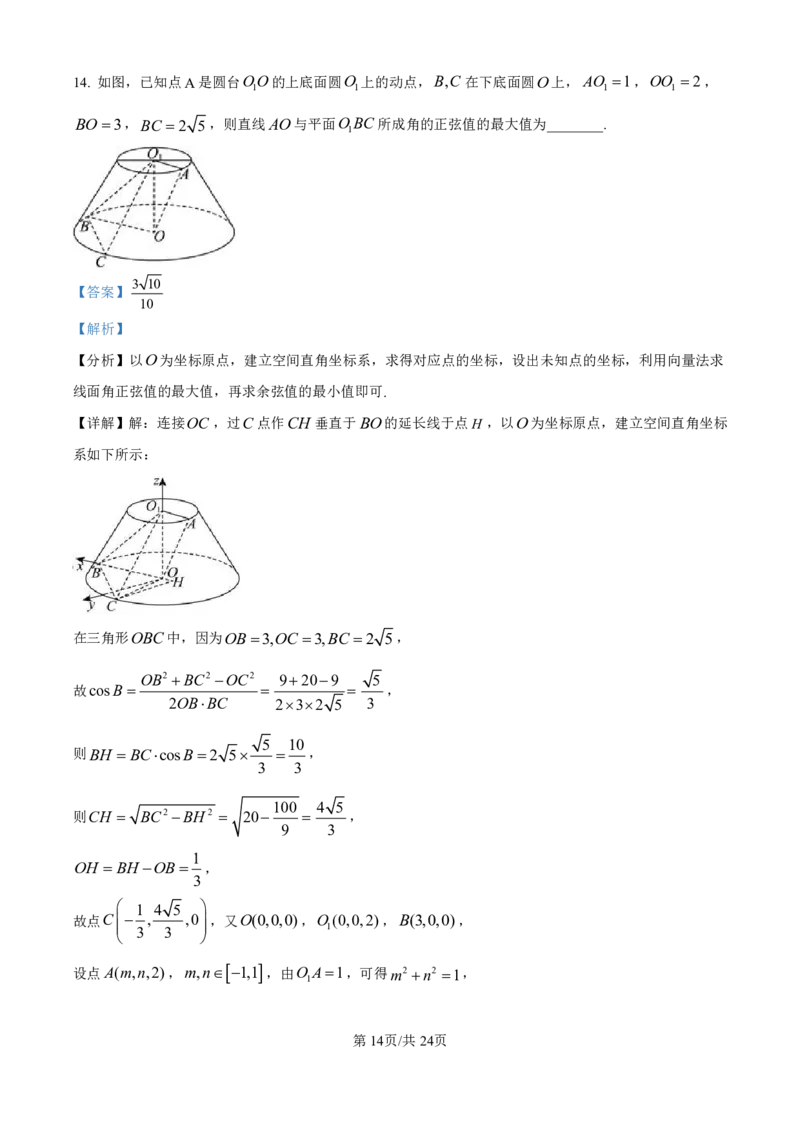14. 如图，已知点A是圆台OO的上底面圆O 上的动点，B,C 在下底面圆O上，AO 1，OO 2， 1 1 1 1 BO3，BC 2 5，则直线AO与平面OBC所成角的正弦值的最大值为________. 1 四、解答题（本题共 5小题，共 77分，解答应写出文字说明、证明过程或演算步骤.） 15. 在Rt△ABC中，BAC 90，BC边上的高AD所在直线的方程为x2y20，A的平分线 所在直线的方程为y0，点B的坐标为  1,3  . （1）求直线BC的方程； （2）求直线AC 的方程及点C的坐标. 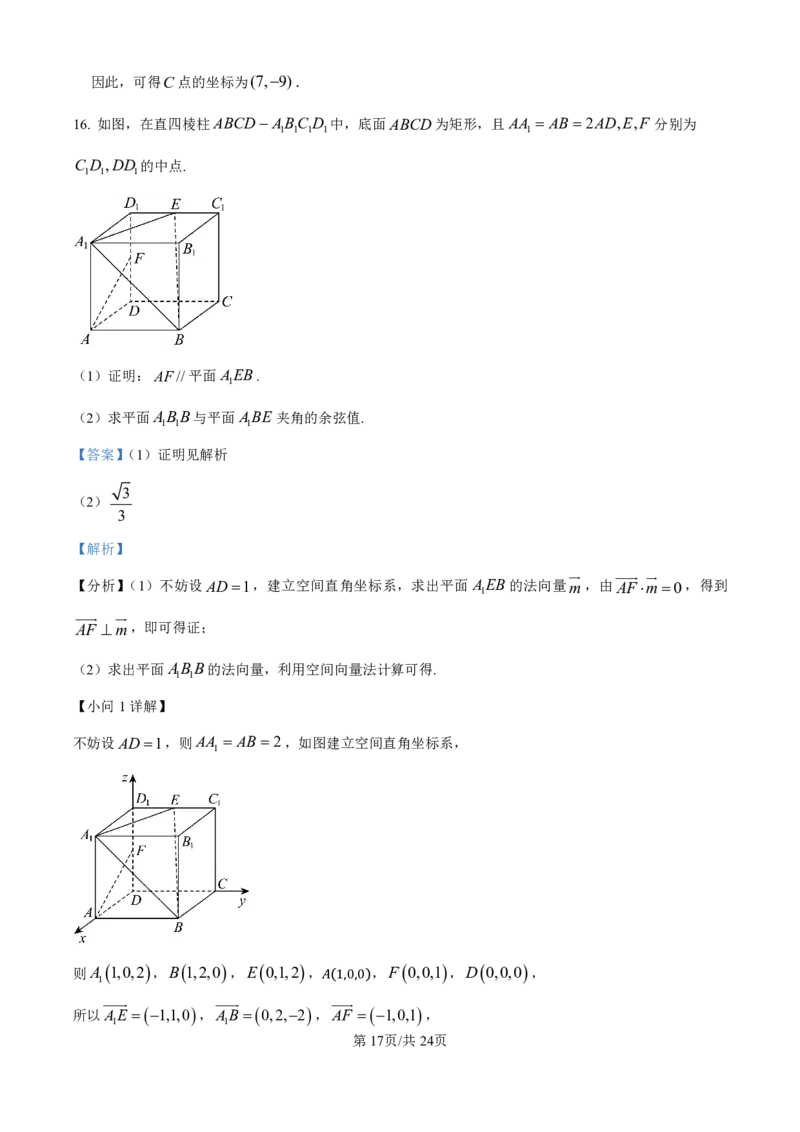16. 如图，在直四棱柱ABCDABC D 中，底面ABCD为矩形，且AA  AB  2AD,E,F 分别为 1 1 1 1 1 C D ,DD 的中点. 1 1 1 第3页/共24页 学科网（北京）股份有限公司（1）证明：AF//平面AEB. 1 （2）求平面ABB与平面ABE 夹角的余弦值. 1 1 1 17. 已知直线l :kx y34k 0  kR 过定点P． 1 （1）求过点P且在两坐标轴上截距的绝对值相等的直线l 方程； 2 （2）若直线l 交x轴正半轴于点A，交 y 轴负半轴于点B，VABC 的面积为S（O为坐标原点），求S的 1 最小值并求此时直线l 的方程． 1 18. 如图，在四棱锥P ABCD中，平面PAD 平面ABCD，PA PD，AB AD ，PA PD，AB 1， AD2，AC CD  5. （1）求证：PD平面PAB . （2）求直线PB与平面PCD所成角的正弦值. AM （3）在棱PA上是否存在点M ，使得BM//平面PCD?若存在，求出 的值；若不存在，请说明理由. AP   19. 在空间直角坐标系Oxyz中，已知向量u  a,b,c  ，点P  x ,y ,z  若直线l以u为方向向量且经过 0 0 0 0 xx yy zz  点P ，则直线l的标准式方程可表示为 0  0  0 （abc0）；若平面以u为法向量且经 0 a b c 过点P ，则平面的点法式方程表示为a  xx b  y y c  zz 0. 0 0 0 0 x1 y2 z （1）已知直线l的标准式方程为   ，平面的点法式方程可表示为 3x yz50， 1  3 2 1 第4页/共24页 学科网（北京）股份有限公司求直线l与平面所成角的余弦值； 1 （2）已知平面 的点法式方程可表示为2x3yz20，平面外一点P  1,2,1  ，点P到平面 的距 2 2 离； （3）（ⅰ）若集合M   x,y,z  | x  y 2, z 1  ，记集合M 中所有点构成的几何体为S，求几何体S 的体积： （ⅱ）若集合N   x,y,z  | x  y 2, y  z 2, z  x 2  .记集合N中所有点构成的几何体为T ，求 几何体T 相邻两个面（有公共棱）所成二面角的余弦值. 2024-2025 学年度高二年级上学期综合素质评价二 数学学科 主命题人 韩艳伟 一、单选题（每题 5 分，共 40 分.在每小题给出的四个选项中，只有一项符合题意.请将正确 答案的序号填涂在答题卡上） 3x y30 1. 直线 的倾斜角为（ ） π π π 2π A. B. C. D. 3 6 4 3 【答案】A 【解析】 【分析】先求出直线斜率，再根据倾斜角的范围即可求解. 【详解】设直线的 3x y30的倾斜角为，且 0,π  ， π 直线 3x y30的斜率k  tan 3，所以 ， 3 故选：A   2. 已知直线a的方向向量为a，平面的法向量为n，下列结论成立的是（ ）     A. 若a//n，则a// B. 若an，则a      C. 若a//n，则a  D. 若an，则a// 【答案】C 第5页/共24页 学科网（北京）股份有限公司【解析】 【分析】根据题意，结合直线的方向向量和平面分法向量的关系，逐项判定，即可求解.   【详解】因为直线a的方向向量为a，平面的法向量为n，   由a//n，可得a ，所以A不正确，C正确；   对于B中，由an，可得a//或a，所以B、D都不正确； 故选：C. 3. 已知圆C:x2  y2 mx10的面积为π，则m（ ） A. 2 B. 2 2 C. 4 2 D. 8 【答案】B 【解析】 【分析】由题意确定圆的半径，结合圆的面积公式建立方程，解之即可求解.  m 2 m2 【详解】因为圆C:x2  y2 mx10，即 x   y2  1，  2  4 m2 所以S πr2 ( 1)π π，解得m2 2. 4 故选：B. 4. 已知两点A 3,2  ，B  2,1  ，过点P  0,1  的直线l与线段AB（含端点）有交点，则直线l的斜率的 取值范围为（ ）  1  1  A. ,1    1, B. 1, 1 C.  ,   1, D.   ,1   5  5  【答案】A 【解析】 【分析】求出直线PA、PB的斜率后可求直线l的斜率的范围. 【详解】 12 11 k  1，而k  1， PA 03 PB 02 第6页/共24页 学科网（北京）股份有限公司故直线l的取值范围为 ,1 (1,)， 故选：A. 5. 已知A(0,1,1)，B(2,1,0)，C(3,5,7)，D(1,2,4)，则直线AB和直线CD所成角的余弦值为（ ） 5 22 5 22 2 22 2 22 A. B.  C. D.  66 66 33 33 【答案】A 【解析】   【分析】算得AB  2,2,1  ,CD  2,3,3 ，结合向量夹角的坐标公式即可求解.   【详解】AB  2,2,1  ,CD  2,3,3 ，     ABCD 463 5 22 所以直线AB和直线CD所成角的余弦值为 cos AB,CD      . AB CD 3 499 66 故选：A. 6. 在棱长为2的正方体ABCDABC D 中，E，F 分别为棱AA ，BB 的中点，G为棱AB 上的一点， 1 1 1 1 1 1 1 1 且AG  02  ，则点G到平面DEF的距离为（ ） 1 1 3 2 2 2 5 A. B. 2 C. D. 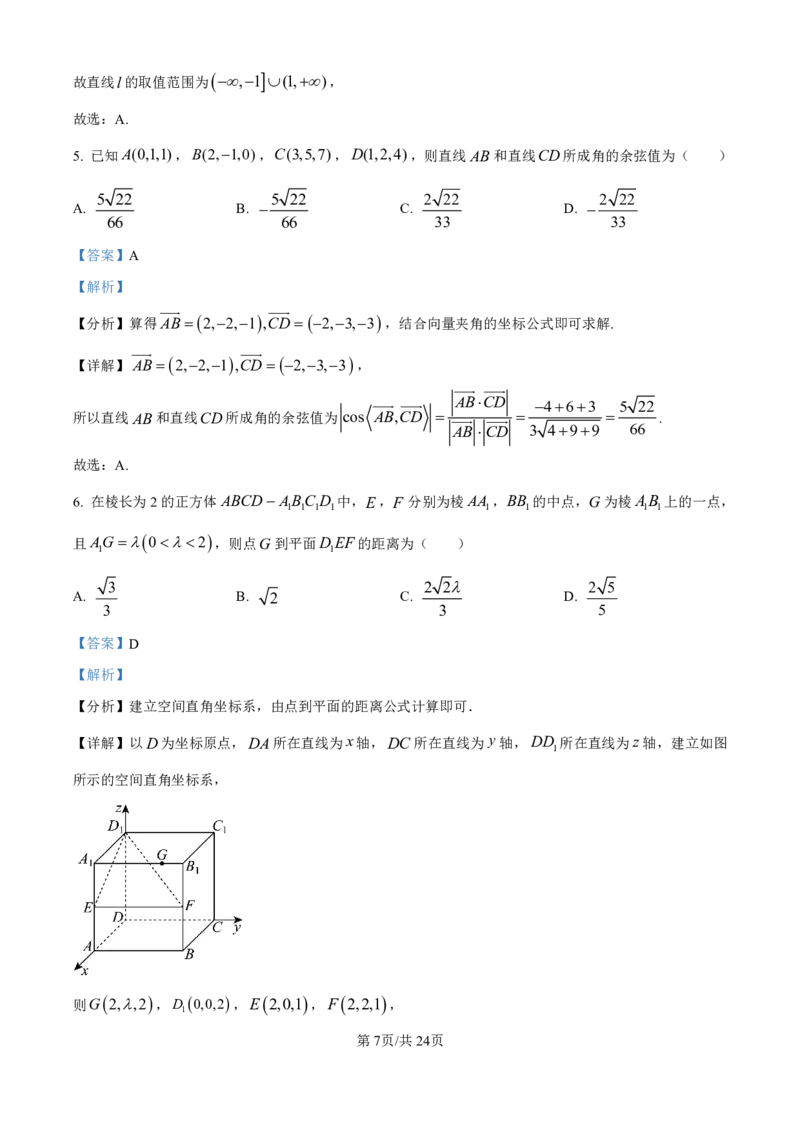3 3 5 【答案】D 【解析】 【分析】建立空间直角坐标系，由点到平面的距离公式计算即可． 【详解】以D为坐标原点，DA所在直线为x轴，DC所在直线为 y 轴，DD 所在直线为z轴，建立如图 1 所示的空间直角坐标系， 则G  2,,2  ，D 0,0,2，E  2,0,1  ，F  2,2,1  ， 1 第7页/共24页 学科网（北京）股份有限公司   所以ED 2,0,1 ，EF  0,2,0 ，EG  0,,1 ． 1     nED 2xz  0 设平面DEF的法向量为n  x,y,z  ，则  1 ， 1  nEF  2y 0 r 取x1，得n  1,0,2  ，   EGn 2 2 5 所以点G到平面D 1 EF的距离为d     ， n 5 5 故选：D． 7. 若动点M  x ,y  ，N  x ,y  分别在直线x y70与直线x y50上移动，则MN的中点P到 1 1 2 2 原点的距离的最小值为（ ） A. 2 3 B. 3 3 C. 3 2 D. 2 2 【答案】C 【解析】 【分析】先求出点P的轨迹，再利用点到直线的距离公式求解. 【详解】解：由题意知，MN的中点P的轨迹为平行于两直线且到两直线距离相等的直线，故其方程为 x y60， 6 P到原点的距离的最小值为d  3 2． 12+12 故选：C 8. 边长为1的正方体ABCD ABC D 中，E，F 分别是AA ，AD 中点，M 是DB靠近B的四等分 1 1 1 1 1 1 1       点，P在正方体内部或表面，DP EF MF 0，则 DP 的最大值是（ ） 5 A.1 B. C. 2 D. 3 2 【答案】D 【解析】 3 3 3 【分析】建立空间直角坐标系，设P  x,y,z  ，从而求得 x y z  0，再根据向量模长公式结合 4 4 2 0 x1,0 y1即可求解. 第8页/共24页 学科网（北京）股份有限公司【详解】   如图，建立空间直角坐标系，设P x,y,z ，  1 1  3 3    则D 0,0,0 ,E1,0, ,F ,0,1,M  , ,0，  2 2  4 4    1 1   1 3     3 3 3 所以EF    ,0, ,MF    , ,1，则EF MF    , , ，  2 2  4 4   4 4 2       因为DP EF MF  0，又DP  x,y,z ， 3 3 3 x y 所以 x y z 0，即z  ， 4 4 2 2  2  x y 2 所以 DP  x2  y2 z2  x2  y2    ，  2   x y 2 11 2 又0 x1,0 y1，所以x2  y2    11   3，当且仅当x y 1，此时z 1时，  2   2  等号成立，  所以 DP 的最大值是 3. 故选：D. 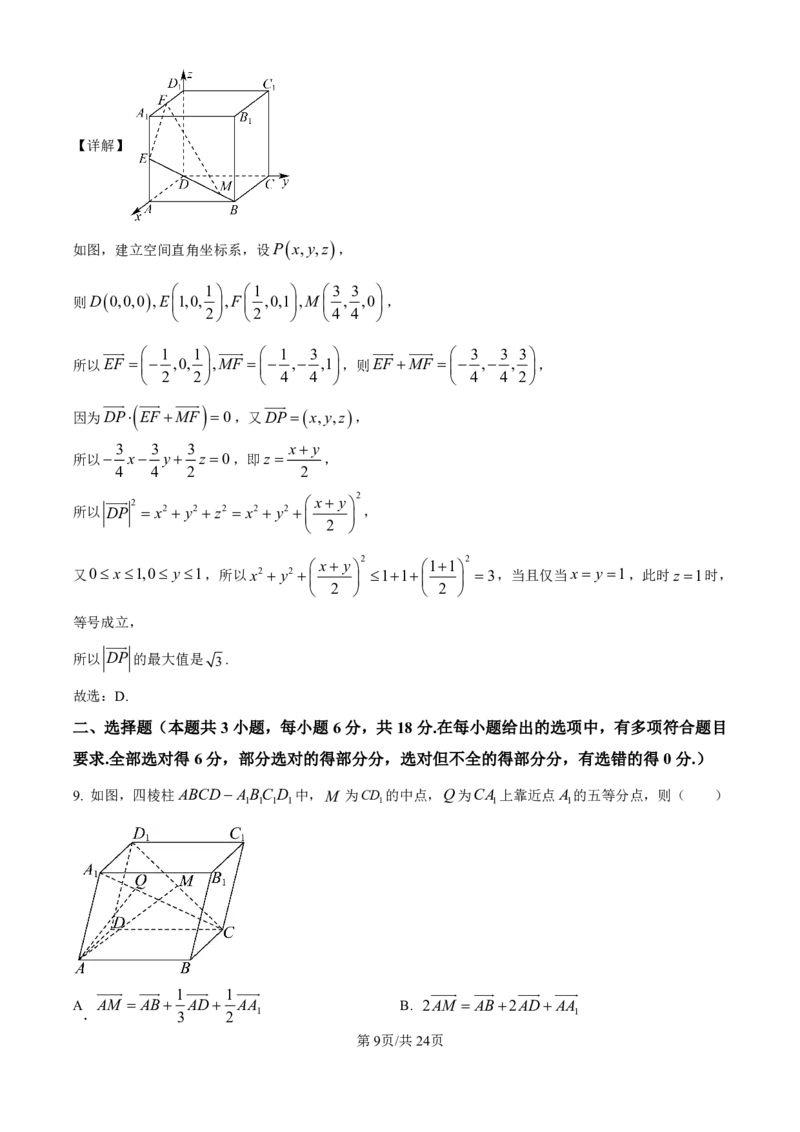二、选择题（本题共 3小题，每小题6 分，共 18分.在每小题给出的选项中，有多项符合题目 要求.全部选对得 6分，部分选对的得部分分，选对但不全的得部分分，有选错的得 0分.） 9. 如图，四棱柱ABCD ABC D 中，M 为CD 的中点，Q为CA 上靠近点A的五等分点，则（ ） 1 1 1 1 1 1 1   1 1     A AM  AB AD AA B. 2AM  AB2ADAA . 3 2 1 1 第9页/共24页 学科网（北京）股份有限公司 1 3 3     C. AQ  AB AD AA D. 5AQ  ABAD4AA 5 4 5 1 1 【答案】BD 【解析】 【分析】运用空间向量的基底表示，结合平面向量的三角形法则和线性运算规则可解. 【 详 解 】       1      1 1 1  1 AM  ABBCCM  AB AD CDCC  AB AD AB AA  AB AD AA ， 2 1 2 2 1 2 2 1     即2AM  AB2ADAA ，故A错误、B正确； 1     1  1     AQ  AA  AQ AA  AC  AA  AD  DC C C 1 1 1 5 1 1 5 1 1 1 1 1  1     1 1 4  AA  AD AB AA  AB AD AA ， 1 5 1 5 5 5 1     即5AQ  ABAD4AA ，故C错误，D正确. 1 故选：BD. 10. 已知两条直线l ，l 的方程分别为3x4y120与ax8y110，下列结论正确的是（ ） 1 2 7 A. 若l //l ，则a6 B. 若l //l ，则两条平行直线之间的距离为 1 2 1 2 4 32 C. 若l l ，则a  D. 若a 6，则直线l ，l 一定相交 1 2 1 2 3 【答案】AD 【解析】 【分析】根据两直线平行求出a的值，可判断A选项；利用平行线间的距离公式可判断B选项；根据两直 线垂直求出a的值，可判断C选项；根据两直线相交求出a的范围，可判断D选项. 【详解】两条直线l ，l 的方程分别为3x4y120与ax8y110，它们不重合， 1 2 若l //l ，则4a 38，得a6，检验符合，故A选项正确； 1 2 若l //l ，由A选项可知，l ：6x8y110，直线l 的方程可化为6x8y240， 1 2 2 1 1124 7 故两条平行直线之间的距离为  ，故B选项不正确； 3664 2 32 若l l ，则3a480，得a  ，故C选项不正确； 1 2 3 由A选项知，当a6时，l //l ，所以若a 6，则直线l ，l 一定相交，故D选项正确. 1 2 1 2 故选：AD. 第10页/共24页 学科网（北京）股份有限公司11. 如图，在多面体ABCDES中，SA平面ABCD，四边形ABCD是正方形，且DE//SA， SA AB2DE 2，M，N 分别是线段BC，SB的中点，Q是线段DC上的一个动点（含端点D，C）， 则下列说法正确的是（ ） A. 存在点Q，使得NQSB B. 存在点Q，使得异面直线NQ与SA所成的角为60o 2 C. 三棱锥Q AMN 体积的最大值是 3 D. 当点Q自D向C处运动时，直线DC与平面QMN所成的角逐渐增大 【答案】ACD 【解析】 【分析】建立空间直角坐标系，设出点Q的坐标，利用向量垂直的坐标运算判断A，利用异面直线的向量 夹角公式计算判断B，连接AQ,AM,AN ，结合锥体体积公式，利用等体积法判断C，利用向量的坐标运 1 sin 算表示线面角的正弦值  5 2 3 ，然后利用二次函数及正弦函数的单调性即可判断D. 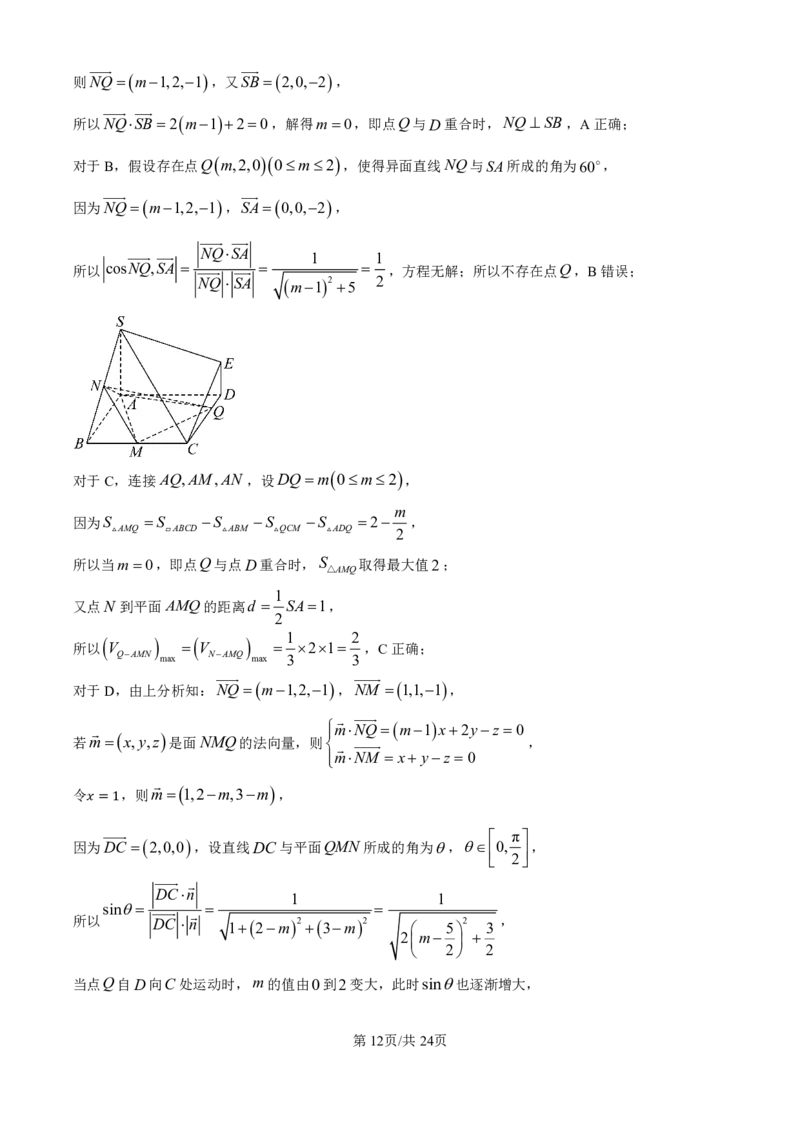2m    2 2    【详解】以A为坐标原点，AB,AD,AS 正方向为x,y,z轴，可建立如图所示空间直角坐标系，               ，B 2,0,0 ，C 2,2,0 ，D 0,2,0 ，E 0,2,1 ，S 0,0,2 ，N 1,0,1 ，M 2,1,0 ； 0,0,0 对于A，假设存在点Q  m,2,0  0m2  ，使得NQSB， 第11页/共24页 学科网（北京）股份有限公司  则NQ  m1,2,1 ，又SB  2,0,2 ，   所以NQSB 2  m1 20，解得m0，即点Q与D重合时，NQSB，A正确； 对于B，假设存在点Q  m,2,0  0m2  ，使得异面直线NQ与SA所成的角为60o，   因为NQ  m1,2,1 ，SA 0,0,2 ，     NQSA 1 1 所以 cosNQ,SA      ，方程无解；所以不存在点Q，B错误； NQ  SA  m1 2 5 2 对于C，连接AQ,AM,AN ，设DQm  0m2  ， m 因为S  S S S S 2 ， AMQ ABCD ABM QCM ADQ 2 所以当m0，即点Q与点D重合时，S 取得最大值2； △AMQ 1 又点N 到平面AMQ的距离d  SA1， 2     1 2 所以 V  V  21 ，C正确； QAMN max NAMQ max 3 3   对于D，由上分析知：NQ  m1,2,1 ，NM  1,1,1 ，     mNQ  m1  x2yz  0 若m x,y,z  是面NMQ的法向量，则  ，  mNM  x yz  0  令 ，则m 1,2m,3m  ， =1   π 因为DC  2,0,0 ，设直线DC与平面QMN所成的角为，  0,  ，  2   DCn 1 1 sin     所以 DC  n 1 2m 2 3m 2  5 2 3 ， 2m    2 2 当点Q自D向C处运动时，m的值由0到2变大，此时sin也逐渐增大， 第12页/共24页 学科网（北京）股份有限公司 π 因为 y sinx在  0,  为增函数，所以也逐渐增大，故D正确.  2 故选：ACD 三、填空题（本题共 3小题，每题 5分，共 15分.） 12. 已知点P  4,2  ，点A为圆x2  y2 4上任意一点，则PA连线的中点轨迹方程是___________． 【答案】x22 y12 1 【解析】   【分析】首先设中点坐标为Q x,y ，再设出相关点A的坐标，代入圆的方程，即可求解. 【详解】设PA连线的中点为Q  x,y  ，则A  2x4,2y2  ， 则 2x4 2  2y2 2 4，即 x2 2  y1 2 1. 故答案为： x2 2  y1 2 1 13. 已知点P(2,1)和直线l:(12)x(13)y20，则点P到直线l的距离的取值范围是 ______________.  【答案】 0, 13  【解析】 【分析】先求得直线l的定点，进而求得点P到直线l的最大距离，然后检验点P(2,1)是否可能在直线l上 即可 【详解】l:(12)x(13)y20可化为：x y2 2x3y1 0  x y20 设直线l的定点为A，点P到直线l的距离为d ，则有： 2x3y10 可得：A  1,1  为直线l的定点 则有： PA  32 22  13，此时 PA为点P到直线l的最大距离 若P(2,1)在直线l上，则有：212431 0，即50 可得：P(2,1)不可能在直线l上，则有：d 0 综上可得：0d  13  故答案为： 0, 13  第13页/共24页 学科网（北京）股份有限公司14. 如图，已知点A是圆台OO的上底面圆O 上的动点，B,C 在下底面圆O上，AO 1，OO 2， 1 1 1 1 BO3，BC 2 5，则直线AO与平面OBC所成角的正弦值的最大值为________. 1 3 10 【答案】 10 【解析】 【分析】以O为坐标原点，建立空间直角坐标系，求得对应点的坐标，设出未知点的坐标，利用向量法求 线面角正弦值的最大值，再求余弦值的最小值即可. 【详解】解：连接OC，过C点作CH 垂直于BO的延长线于点H ，以O为坐标原点，建立空间直角坐标 系如下所示： 在三角形OBC中，因为OB3,OC 3,BC 2 5， OB2 BC2 OC2 9209 5 故cosB    ， 2OBBC 232 5 3 5 10 则BH  BCcosB2 5  ， 3 3 100 4 5 则CH  BC2BH2  20  ， 9 3 1 OH  BH OB ， 3  1 4 5  故点C , ,0，又O(0,0,0)，O (0,0,2)，B(3,0,0)，  3 3  1   设点A(m,n,2)，m,n1,1  ，由O A1，可得m2 n2 1， 1 第14页/共24页 学科网（北京）股份有限公司  10 4 5   BC  , ,0，BO 3,0,2 ，  3 3  1   设平面OBC的法向量 ， 1 = , ,    10 4 5  mBC  0  x y 0 则   ，即 3 3 ， mBO 1  0   3x2z 0 取 y  5，则x2,z 3，    故平面OBC的法向量m 2, 5,3 ， 1  又OA m,n,2 ，  π 设直线AO与平面O 1 BC所成角为，   0, 2   ，    m  OA 2m 5n6 2m 5n6 则sin cosOA,m     ，  m OA 3 2 m2n24 3 10 因为m,n1,1  ，且m2 n2 1， 故令mcos，nsin，(0,2)， 则2m 5n6 5sin2cos63sin 6 ，tan 2 5 ，    π , π ， 5  2 2 又(0,2)，所以sin()1,1  ， 3sin()6 3,9  ，即2m 5n6 3,9 ， 9 3 10 所以sin的最大值为  . 3 10 10 3 10 故答案为： . 10 四、解答题（本题共 5小题，共 77分，解答应写出文字说明、证明过程或演算步骤.） 15. 在Rt△ABC中，BAC 90，BC边上的高AD所在直线的方程为x2y20，A的平分线 所在直线的方程为y0，点B的坐标为  1,3  . 第15页/共24页 学科网（北京）股份有限公司（1）求直线BC的方程； （2）求直线AC 的方程及点C的坐标. 【答案】（1）2x y50 （2）直线AC 的方程为：y  x 2，C(7,9) 【解析】 【分析】（1）根据垂直的位置关系，算出直线BC的斜率为2，利用直线方程的点斜式列式，化简整理 即可得到直线BC的方程； （2）由BC边的高所在直线方程和y0，解出A(2,0)，从而得出直线AB的方程．由直线AC 、AB 关于直线 y0对称，算出AC 方程，最后将AC 方程与BC方程联解，即可得出点C的坐标． 【小问1详解】 1 由于AD所在直线的方程为x2y20，故AD的斜率为 ， 2 BC与AD互相垂直，直线BC的斜率为k 2， 结合B(1,3)，可得BC的点斜式方程： y32(x1)， 化简整理，得2x y50，即为所求的直线BC方程． 【小问2详解】 由x2y20和y0联解，得A(2,0) y0 x2 由此可得直线AB方程为：  ，即 y  x2， 30 12 AB，AC 关于角A平分线x轴对称， 直线AC 的方程为：y  x 2， 直线BC方程为 y 2x5， 将AC 、BC方程联解，得x 7， y9， 第16页/共24页 学科网（北京）股份有限公司因此，可得C点的坐标为(7,9)． 16. 如图，在直四棱柱ABCDABC D 中，底面ABCD为矩形，且AA  AB  2AD,E,F 分别为 1 1 1 1 1 C D ,DD 的中点. 1 1 1 （1）证明：AF//平面AEB. 1 （2）求平面ABB与平面ABE 夹角的余弦值. 1 1 1 【答案】（1）证明见解析 3 （2） 3 【解析】    【分析】（1）不妨设 AD1，建立空间直角坐标系，求出平面 AEB的法向量m，由AFm0，得到 1   AF m，即可得证； （2）求出平面ABB的法向量，利用空间向量法计算可得. 1 1 【小问1详解】 不妨设AD1，则AA  AB  2，如图建立空间直角坐标系， 1           则A 1,0,2 ，B 1,2,0 ，E 0,1,2 ， ，F 0,0,1 ，D 0,0,0 ， 1   1,0,0 所以AE 1,1,0 ，AB  0,2,2 ，AF 1,0,1 ， 1 1 第17页/共24页 学科网（北京）股份有限公司设 是平面AEB的一个法向量， 1  = , ,  mAE x y  0 则  1  ，取x1，则 y  z 1，  mAB  2y2z 0 1  所以平面AEB的一个法向量m 1,1,1  ， 1     又AFm0，所以AF m，因为AF 平面AEB，所以AF//平面AEB. 1 1 【小问2详解】  因为DA平面AABB，所以DA 1,0,0 是平面ABB的一个法向量， 1 1 1 1     mDA 1 3 又因为cos m,DA      ， m DA 3 3 3 所以平面ABB与平面ABE 夹角的余弦值为 . 1 1 1 3 17. 已知直线l :kx y34k 0  kR 过定点P． 1 （1）求过点P且在两坐标轴上截距的绝对值相等的直线l 方程； 2 （2）若直线l 交x轴正半轴于点A，交 y 轴负半轴于点B，VABC 的面积为S（O为坐标原点），求S的 1 最小值并求此时直线l 的方程． 1 【答案】（1）x y10或x y70或3x4y 0 （2）最小值为24，直线l :3x4y240 1 【解析】 【分析】（1）求出直线l 过的定点，分a0，b  0和a b0两种情况，当a0，b  0时，设l的方 1 x y 程为  1，根据Q点  4,3  在直线上求出直线方程，若a b，求出直线方程，若a  b，求出直 a b 线方程，当a b0，根据直线过原点，且过点  4,3  求出直线的方程； （2）求出直线l 交x轴的正半轴的点，交 y 轴的负半轴的点，求出VAOB的面积，根据基本不等式求出S 1 的最小值时k的值. 【小问1详解】 直线l : y3 k  x4 ，则直线l 过定点P  4,3  ， 1 1 第18页/共24页 学科网（北京）股份有限公司x y ①当a0，b  0时，设l的方程为  1． a b 4 3 Q点  4,3  在直线上，  1． a b 若a b，则ab1， 直线的方程为x y 1， 若a  b，则a7，b7， 直线的方程为x y 7； ②当a b0时，直线过原点，且过点  4,3  ， 直线的方程为3x4y 0， 综上所述，所求直线l的方程为x y10或x y70或3x4y 0； 【小问2详解】 4k3 令y0，则x ；令x0，则 y 4k3， k 4k3  直线l 交x轴的正半轴于点A ,0，交 y 轴的负半轴于点B  0,4k 3 ，k0， 1  k  O为坐标原点，设VAOB的面积为S， 1 1 4k3 1  9 1  9  则S  OAOB   4k3   16k24     242 16k   24， 2 2 k 2  k  2  k  9 3 当且仅当16k  时，即k  时取等号， k 4 3 故S的最小值为24，此时k  ， 4 直线l :3x4y240． 1 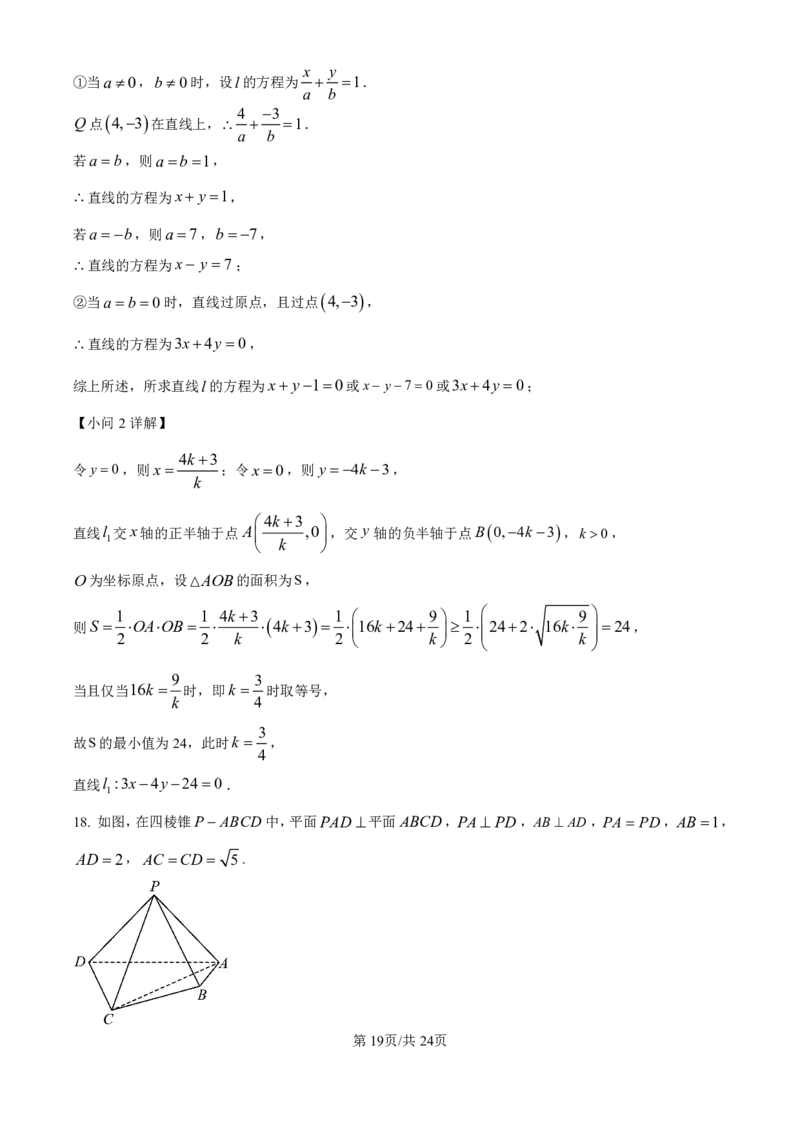18. 如图，在四棱锥P ABCD中，平面PAD 平面ABCD，PA PD，AB AD ，PA PD，AB 1， AD2，AC CD  5. 第19页/共24页 学科网（北京）股份有限公司（1）求证：PD平面PAB. （2）求直线PB与平面PCD所成角的正弦值. AM （3）在棱PA上是否存在点M ，使得BM//平面PCD?若存在，求出 的值；若不存在，请说明理由. AP 【答案】（1）证明见解析 3 （2） 3 1 （3）存在； 4 【解析】 【分析】（1）根据面面垂直的性质可得AB 平面PAD，进而得ABPD，再结合线面垂直的判定定理 进行证明即可； （2）建立空间直角坐标系，求出平面PCD的一个法向量，再利用空间向量夹角公式、线面角的定义进行求 解即可；   （3）要使BM//平面PCD，则BMn0，由此列式求解可得. 【小问1详解】 ∵平面PAD 平面ABCD，且平面PAD平面ABCD AD， 且AB AD，AB平面ABCD， ∴AB 平面PAD， ∵PD 平面PAD，∴ABPD， 又PD  PA，且PAAB  A，PA,AB平面PAB， ∴PD平面PAB； 【小问2详解】 取AD中点为O，连接CO,PO， 又∵PA PD，∴PO AD．则AOPO1， ∵CD  AC  5，∴CO AD，则CO  AC2OA2  51 2，    以O为坐标原点，分别以OC,OA,OP所在直线为x,y,z轴建立如图所示的空间直角坐标系Oxyz， 则P(0,0,1)，B(1,1,0)，D(0,1,0)，C(2,0,0)，     则PB(1,1,1)，PD(0,1,1)，PC (2,0,1)，CD (2,1,0)， 设 为平面PCD的一个法向量， = , , 第20页/共24页 学科网（北京）股份有限公司   nPD 0 yz 0  1  则由   ，得 ，令z 1，则n   ,1,1． nPC 0 2xz 0 2  设PB与平面PCD的夹角为， 1   11   nPB 2 3 则sin cosn,PB     ；  n‖PB 1 3 11 3 4 【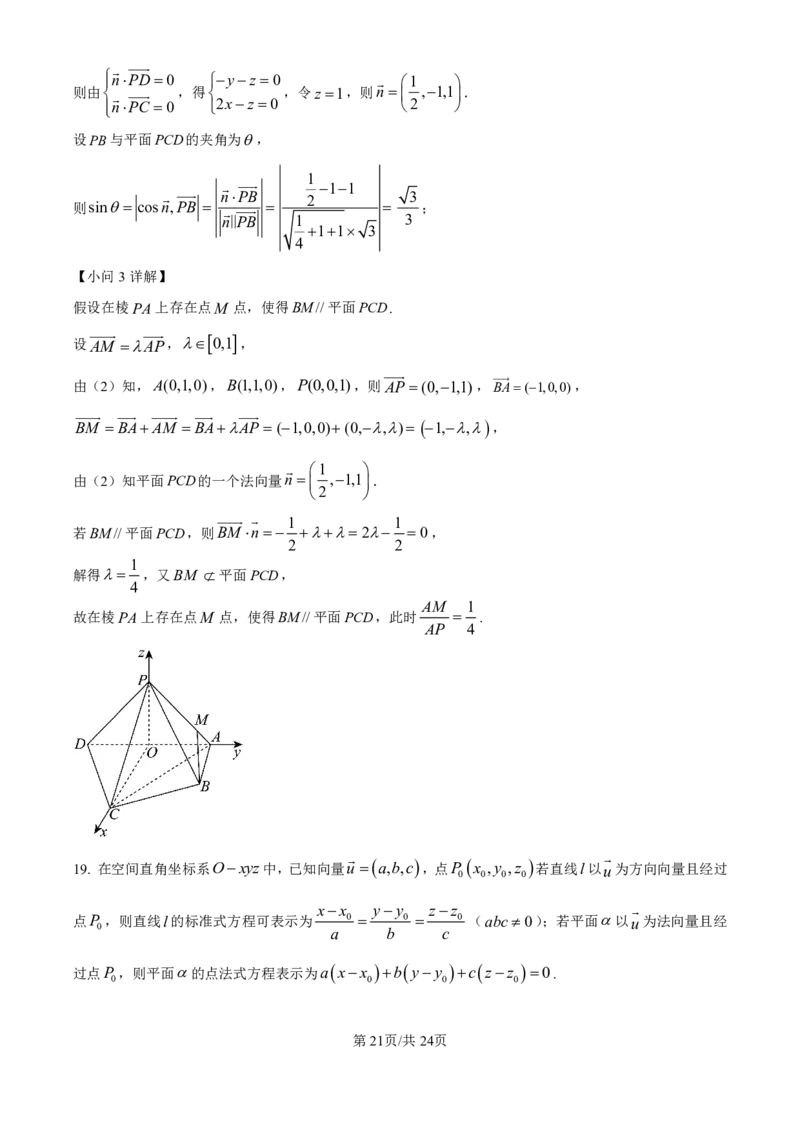小问3详解】 假设在棱PA上存在点M 点，使得BM//平面PCD.   设AM AP， 0,1  ，  uur 由（2）知，A(0,1,0)，B(1,1,0)，P(0,0,1)，则AP (0,1,1)，BA(1,0,0)，      BM BAAM BAAP  (1,0,0) (0,,) 1,,，  1  由（2）知平面PCD的一个法向量n   ,1,1． 2    1 1 若BM//平面PCD，则BM n  2  0， 2 2 1 解得 ，又BM  平面PCD， 4 AM 1 故在棱PA上存在点M 点，使得BM//平面PCD，此时  . AP 4   19. 在空间直角坐标系Oxyz中，已知向量u  a,b,c  ，点P  x ,y ,z  若直线l以u为方向向量且经过 0 0 0 0 xx yy zz  点P ，则直线l的标准式方程可表示为 0  0  0 （abc0）；若平面以u为法向量且经 0 a b c 过点P ，则平面的点法式方程表示为a  xx b  y y c  zz 0. 0 0 0 0 第21页/共24页 学科网（北京）股份有限公司x1 y2 z （1）已知直线l的标准式方程为   ，平面的点法式方程可表示为 3x yz50， 1  3 2 1 求直线l与平面所成角的余弦值； 1 （2）已知平面 的点法式方程可表示为2x3yz20，平面外一点P  1,2,1  ，点P到平面 的距 2 2 离； （3）（ⅰ）若集合M   x,y,z  | x  y 2, z 1  ，记集合M 中所有点构成的几何体为S，求几何体S 的体积： （ⅱ）若集合N   x,y,z  | x  y 2, y  z 2, z  x 2  .记集合N中所有点构成的几何体为T ，求 几何体T 相邻两个面（有公共棱）所成二面角的余弦值. 3 10 【答案】（1） 10 14 （2） 2 2π （3）（i）16，（ii） 3 【解析】 【分析】（1）利用题中概念分别计算出直线方向向量与平面法向量，然后利用线面角与直线方向向量和平 面法向量所成角的关系计算即可； （2）先计算平面法向量，找到平面上一点A然后利用向量的投影计算即可； （3）（i）先建立等式，然后画出所表示的面，计算所围成的图形的面积即可；（ii）因为是一个完全对称的 图形，只需计算第一卦限内相邻面的二面角，我们需要画出第一卦限内图象，得到其二面角为钝角； 【小问1详解】   由题可知，直线l的一个方向向量坐标为m (1, 3,2)，平面的一个法向量为n ( 3,1,1)， 1   |mn| 2 10 设直线l与平面所成角为，则有sin     ， 1 |m||n| 8 5 10 所以cos 3 10 ，直线l与平面所成角的余弦值为 3 10 . 1 10 10 【小问2详解】  由题可知平面 的法向量为n (2,3,1)，且过点A(0,0,2)， 2 2 第22页/共24页 学科网（北京）股份有限公司   |n AP| 7 14 因为P(1,2,1),所以AP(1,2,1)，所以点P到平面 的距离为 2   . 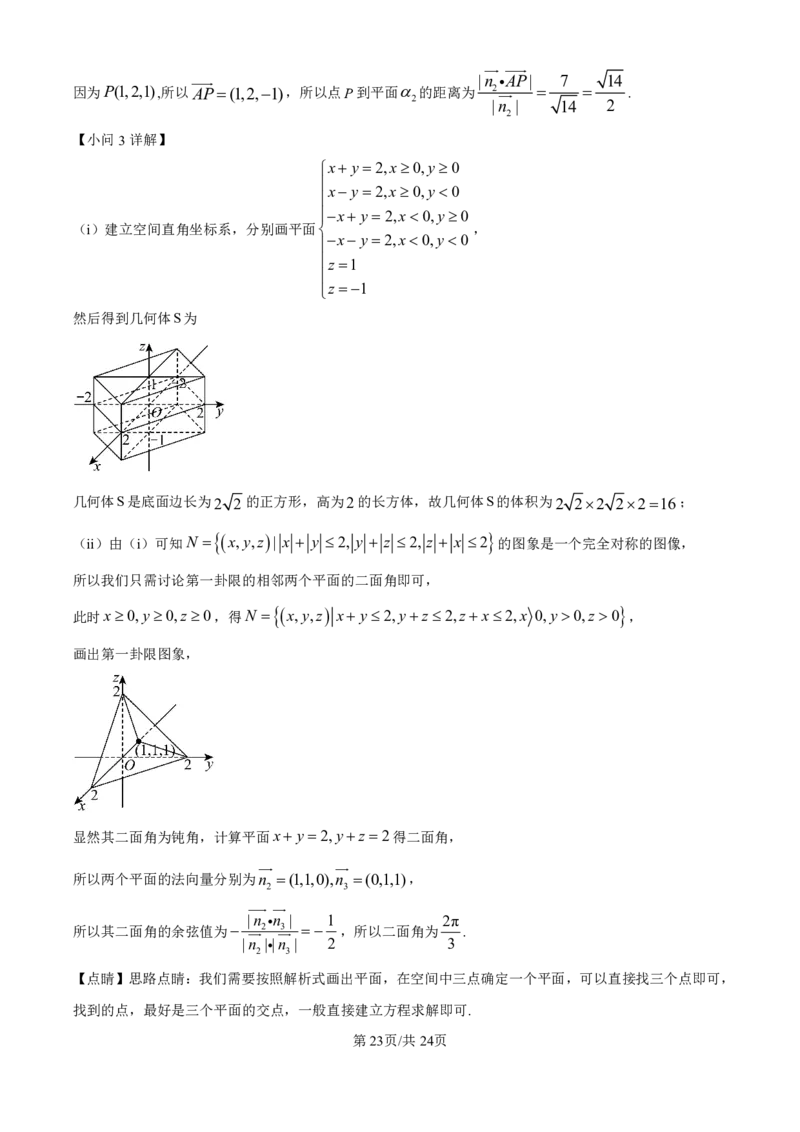2 |n | 14 2 2 【小问3详解】 x y  2,x0,y0  x y  2,x0,y0  x y  2,x 0,y 0 （i）建立空间直角坐标系，分别画平面 ， x y  2,x 0,y 0   z 1  z 1 然后得到几何体S为 几何体S是底面边长为2 2的正方形，高为2的长方体，故几何体S的体积为2 22 2216； （ii）由（i）可知N   x,y,z  | x  y 2, y  z 2, z  x 2  的图象是一个完全对称的图像， 所以我们只需讨论第一卦限的相邻两个平面的二面角即可， 此时x0,y0,z 0，得N   x,y,z  x y2,yz 2,zx2,x 0,y 0,z 0  ， 画出第一卦限图象， 显然其二面角为钝角，计算平面x y 2,yz 2得二面角，   所以两个平面的法向量分别为n (1,1,0),n (0,1,1)， 2 3   |n n | 1 2π 所以其二面角的余弦值为 2 3  ，所以二面角为 . |n ||n | 2 3 2 3 【点睛】思路点睛：我们需要按照解析式画出平面，在空间中三点确定一个平面，可以直接找三个点即可， 找到的点，最好是三个平面的交点，一般直接建立方程求解即可. 第23页/共24页 学科网（北京）股份有限公司第24页/共24页 学科网（北京）股份有限公司