数学-浙江省G12名校协作体2024学年高二第一学期返校联考_2024-2025高二（7-7月题库）_2024年09月试卷_0906浙江省G12名校协作体2024学年高二第一学期返校联考

2024 学年第一学期浙江省名校协作体试题 高二年级数学学科 考生须知： 1．本卷满分150分，考试时间120分钟. 2．答题前，在答题卷指定区域填写学校、班级、姓名、试场号、座位号及准考证号. 3．所有答案必须写在答题卷上，写在试卷上无效. 4．考试结束后，只需上交答题卷. 选择题部分 一､选择题：本题8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合 题目要求． 1．已知集合A={x|x2 4}，B=x|−4x1，则A B=（ ▲ ） A.{x|x2} B.{x|−2x1} C.{x|−4x1} D.{x|−4x2} 2．记复数z的共轭复数为z，若z(2+i)=2−4i，则 z =（ ▲ ） A．1 B． 2 C．2 D．2 2 3．甲、乙两名射击运动员进行射击比赛，甲中靶的概率为0.6，乙中靶的概率为0.7， 且两人是否中靶相互独立，若甲、乙各射击一次，则（ ▲ ） A．两人都中靶的概率为0.12 B．两人都不中靶的概率为0.42 C．恰有一人中靶的概率为0.46 D．至少一人中靶的概率为0.74 1 3  2 2 ( ) ( ) 4．已知向量a= , ，b= , ，若 a+b // a+b ，则（ ▲ ）     2 2 2 2     A. =1 B. =−1 C.+=−1 D. +=1 5．已知,是两个互相垂直的平面，m,n是两条直线， =m则“n//m” 是“n//”的（ ▲ ） A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 6. 设函数 f (x)=x x ，则不等式 f (2log x)+ f (3−log x)0的解集是（ ▲ ） 3 3 A．   1 ,27   B．  0， 1   C．(0，27) D．(27，+) 27   27 试卷第 1页，共4页   2  7．已知函数 f(x)= 2sinx+ 的定义域为a,b，值域为− , 2，  4 2   则b−a的取值范围是（ ▲ ） π 4π π 5π 5π 5π 2π 4π A． , B． , C． , D． ,         2 3  2 3   6 3   3 3  8．如图，在正方体ABCD−ABCD 中，E是棱BC的中点，F 是侧面BCCB 上的动点， 1 1 1 1 1 1 且AF //平面ADE，则下列说法正确的个数有（ ▲ ） 1 1 ①二面角F−AD −E的大小为常数 1 ②二面角F−DE−A的大小为常数 1 ③二面角F−AE−D 的大小为常数 1 A．0个 B．1个 C．2个 D．3个 二、多项选择题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题 目要求．全部选对的得6分，部分选对的得部分分，有选错的得0分． 9．某次校十佳歌手评比中，10位评委给出的分数分别为x,x , ,x ，计算得平均数x=7，方差 1 2 10 S2 =2，现去掉一个最高分10分和一个最低分5分后，对新数据下列说法正确的是（ ▲ ） A．极差变大 B．中位数不变 C．平均数变小 D．方差变大 10．已知a，b，c分别是△ABC三个内角A，B，C的对边，则下列命题中正确的是（ ▲ ） A．若AB，则cosAcosB   B．若B= ，b=1，c= 2，则C= 6 4 C．若O是△ABC所在平面内的一点，且OB−OC = OB+OC−2OA ， 则△ABC是直角三角形  3 D．若B= ，b 1，则ABAC的最大值是 6 2 11．四面体ABCD中,AC =BC = AB=3，BD=5，CD=4，记四面体ABCD外接球的表面积为S， 当AD变化时，则（ ▲ ） 324 A. 当AD=3时，S =  11 B. 当四面体ABCD体积最大时，S =28 C. S 可以是16 D. S 可以是100 试卷第 2页，共4页非选择题部分 三、填空题：本题共3小题，每小题5分，共15分． 12．已知幂函数 f(x)= ( m2 −5m+7 ) xm的图象关于y轴对称，则实数m的值是 ▲ . 13．已知x1,y1且log x=4log 3，则𝑥𝑦的最小值为 ▲ . 3 y 2 14．在正四面体ABCD中，E,F 分别为AB,BC的中点，AG= AD，截面EFG将四面体分成两部 3 分，则体积较大部分与体积较小部分的体积之比是 ▲ . 四、解答题：(共5大题，共77分，其中第15题13分，第16题、第17题每题15分，第18 题、第19题每题17分，解答应写出文字说明､证明过程或演算步骤）．  x−1  15．已知aR,A=x|a(x+a)(x+2)0 ,B=x 0．  x−2  (Ⅰ)当a0时求集合A； (Ⅱ)若B A，求a的取值范围. 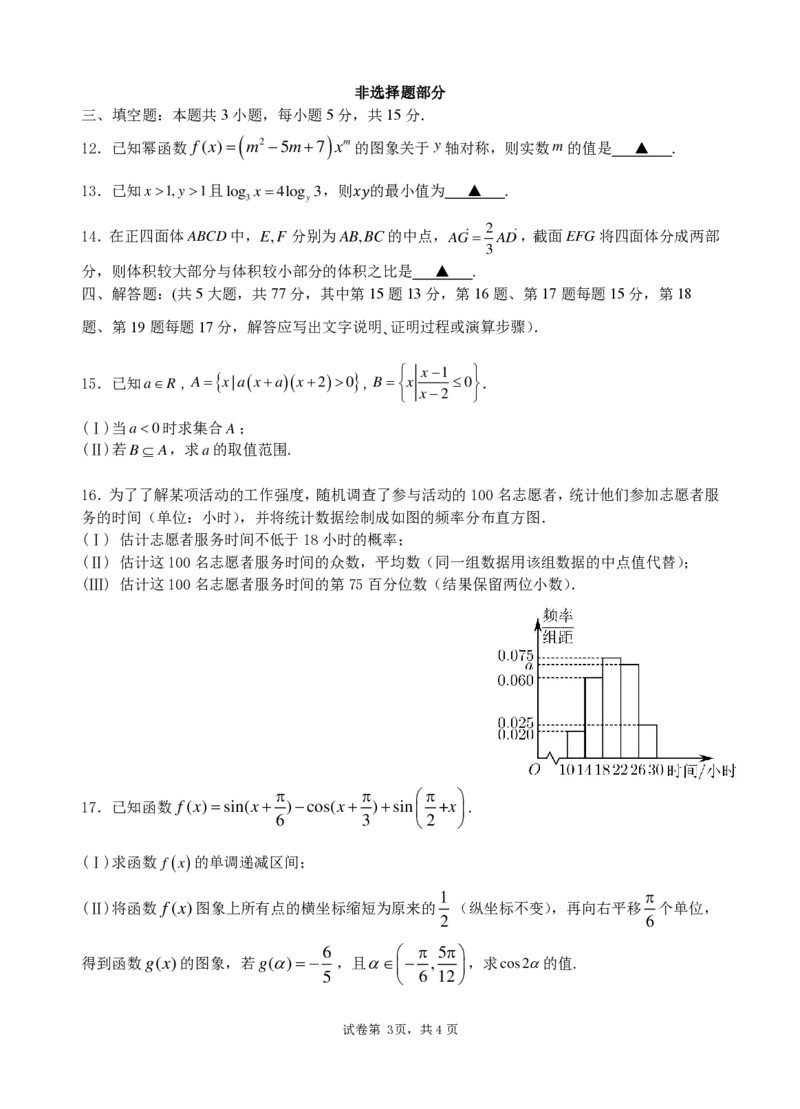16．为了了解某项活动的工作强度，随机调查了参与活动的100名志愿者，统计他们参加志愿者服 务的时间（单位：小时），并将统计数据绘制成如图的频率分布直方图． (Ⅰ) 估计志愿者服务时间不低于18小时的概率； (Ⅱ) 估计这100名志愿者服务时间的众数，平均数（同一组数据用该组数据的中点值代替）； (Ⅲ) 估计这100名志愿者服务时间的第75百分位数（结果保留两位小数）．     17．已知函数 f(x)=sin(x+ )−cos(x+ )+sin  +x . 6 3 2  (Ⅰ)求函数 f (x)的单调递减区间； 1  (Ⅱ)将函数 f(x)图象上所有点的横坐标缩短为原来的 （纵坐标不变），再向右平移 个单位， 2 6 6   5 得到函数g(x)的图象，若g()=− ，且  − , ，求cos2的值. 5  6 12 试卷第 3页，共4页18．如图，已知四棱锥P− ABCD中，PB=PD=4，PA=6，APB=APD=60，且PB⊥PD， (Ⅰ)求证：BD⊥PA； (Ⅱ)求直线PA与平面ABCD所成角的正弦值； (Ⅲ)若平面PAC 与平面ABCD垂直，PC =3，求四棱锥P− ABCD的体积． 19．已知函数 f (x)的定义域为D，若存在常数k(k 0)，使得对D内的任意x，都有 f (x)= f   k ，则称 f (x)是“反比例对称函数”.设 f (x)=log xlog 16 ，g(x)=ax+ 16 −m. x 2 8 x ax 16 (Ⅰ)判断函数 f (x)=log xlog 是否为“反比例对称函数”，并说明理由； 2 8 x (Ⅱ)当a=1时，若函数 f (x)与g(x)的图象恰有一个交点，求m的值； (Ⅲ)当a1时,设h(x)= f (x)−g(x)，已知h(x)在(0,+)上有两个零点x,x ，证明：xx 16. 1 2 1 2 命题： 学军中学 温岭中学（审校） 审核：春晖中学 试卷第 4页，共4页2024 学年第一学期浙江省名校协作体联考参考答案 高二年级数学学科 首命题：学军中学 次命题兼审校：温岭中学 审核：春晖中学 一、选择题： 题号 1 2 3 4 5 6 7 8 答案 B C C A D B D B 二、多选题 题号 9 10 11 答案 BC ACD ABD 三、填空题 题号 12 13 14 答案 2 81 11:7 四、解答题 15．（Ⅰ）∵a0，a(x+a)(x+2)0 所以(x+a)(x+2)0，解得−2x−a 所以A=x −2x−a .............5分 （Ⅱ）B=x1x2 ①当a0时，因为B A，所以−a2，得a−2；............ 7分 ②当a=0时A=不合；.............9分 ③当0a2时，A=  x x−2或x−a  成立，所以B A成立；.............11分 ④当a2时时，A=  x x−a或x−2  成立，所以B A成立； 综合得a−2或a0 ...............................13分 16．解析：（Ⅰ）由已知，志愿者服务时间不低于18小时的概率为1−(0.02+0.06)4=0.68. ------4分 （Ⅱ）由频率分布直方图可看出最高矩形底边上的中点值为20，故众数是20；--------7分 由(0.02+0.06+0.075+a+0.025)4=1，解得a=0.07， ∵(0.02+0.06)4=0.32，且(0.02+0.06+0.075)4=0.62， 平均数为(0.0212+0.0616+0.07520+0.0724+0.02528)4=20.32；--------11分 （Ⅲ）又∵(0.02+0.06+0.075)4=0.62，(0.02+0.06+0.075+0.07)4=0.9， ∴第75%位数位于22~26之间，设第75%位数为y， y−22 0.75−0.62 13 则 = ，解得y=22+ 23.86．----------------15分 26−22 0.9−0.62 7 第 1页 共 4页 17．（Ⅰ）解析： f(x)=2sin(x+ )，----------------------------3分 6    3  4 令x+  2k+ ,2k+ 得2k+ x2k+ ，   6  2 2  3 3  4 f(x)的单调减区间为[ +2k, +2k],kZ -----------------6分 3 3   6 （Ⅱ）解析：由题意得g(x)=2sin(2x− )，则g()=2sin(2− )=− --------8分 6 6 5  3  5   2 sin(2− )=− ，又因为(− , )，则2− (− , ) 6 5 6 12 6 2 3  4 所以cos(2− )= ------------------------------------------------11分 6 5   cos2=cos(2− + ) 6 6 ----------------------15分     3+4 3 =cos(2− )cos −sin(2− )sin = 6 6 6 6 10 18．（Ⅰ）解析：由题意，在三角形PAB与三角形PAD中用余弦定理可得： AB=AD=2 7，-------------------------------------2分 取BD中点M ，连AM,PM，由AB= AD，PB=PD，可得BD⊥ AM ，BD⊥PM ， 故BD⊥平面APM ，因为AP平面APM ，所以BD⊥PA-----------4分 （Ⅱ）因为BD⊥平面APM ，所以平面PAM ⊥平面ABCD，故点P在平面ABCD上的投影在两平 面的交线AM 上，所以PAM 为所求线面角，-----------5分 在RtPBD中，有BM =DM =PM =2 2；在RtADM 中，可得AM =2 5，---------7分 PA2 +AM2 −PM2 2 5 5 故在三角形PAM 中：cosPAM = = ，所以sinPAM = ， 2PAAM 5 5 5 即所求线面角的正弦值为 .------------------------------------------------8分 5 （Ⅲ）解析：因为平面PAM ⊥平面ABCD，故点P,A,M,C四点共面， 所以点A,M,C三点共线，-------------------------------------------------10分 第 2页 共 4页2 5 所以在PAC 中，cosPAC= ，所以PC2 =PA2 +AC2 −2PAACcosPAC=9， 5 24 9 5 即36+AC2 − AC=9，解得AC= 或AC=3 5，---------------------12分 5 5 9 5 若AC= ，则四边形ABCD为凹四边形，矛盾. 所以AC=3 5---------------13分 5 1 因为，所以S = ACBD= 6 10，-----------------------------15分 四边形ABCD 2 1 所以V = S PAsinPAM =12 2.-------------------17分 四棱锥P−ABCD 3 四边形ABCD 19．(Ⅰ)解析：是.理由如下：------------------------------------1分 16 x0, 0, x 16 16 -----------------------3分 ln ln 16 16 x lnx lnx x f( )=log log x=  =  = f(x) x 2 x 8 ln2 ln8 ln2 ln8 16 故 f (x)=log xlog 是“反比例对称函数”.--------------- -------4分 2 8 x (Ⅱ)解析：设h(x)= f (x)−g(x),x(0,+), 16 16 由(Ⅰ)知 f( )= f(x)，验证知g( )=g(x) x x 16 故h(x)=h( ).--------------------------------------------------------6分 x 由题意函数 f (x)与g(x)的图像恰有一个交点，即h(x)恰有一个零点， 故由对称性零点只能为4.-----------------------------------------------7分 20 由h(4)=0，得m= .----------------------------------------8分 3 下检验此时h(x)恰有一个零点. 由对勾函数性质知，g(x)在 (0,4 上单调递减， 4,+) 上单调递增. lnx(ln16−lnx) u(ln16−u) f (x)= ,设u=lnx， f (x)= ， ln2ln8 ln2ln8 f (x)关于u在(0,ln4上单调递增， ln4,+) 上单调递减， 因此 f (x)在 (0,4 上单调递增， 4,+) 上单调递减. 故h(x)在 (0,4 上单调递增， 4,+) 上单调递减. 故此时h(x)恰有一个零点4.----------------------------10分 注:充分必要性步骤交换亦可。充分性也可通过不等式的方法 第 3页 共 4页ln16 2 f (x)= lnx(ln16−lnx)    2   = 4 ,g(x) 4结合取等条件得到 ln2ln8 ln2ln8 3 3 16 法二:g(x)=x+ −m在(0,4为减函数,在4,+)为增函数 x 1 f (x)= log x(4−log x)在(0,4为增函数,4,+)为减函数 3 2 2 记h(x)= f (x)−g(x)则h(x)在(0,4为增函数,4,+)为减函数 x→0时h(x)→−,x→+时h(x)→− h(x)只有一个零点 4 20 所以h(4)= −(8−m)=m− =0 3 3 20 所以m= 3 4  4 (Ⅲ)解析： f (x)在 4,+) 上单调递减，g(x)在  ,+ 上单调递增， a1, 4， a  a 故h(x)在 4,+) 上单调递减.------------------------------------------11分 h(x)在[4,+)上至多有一个零点. 不妨设x x ，下分情况讨论： 1 2 ①0x x 4，xx 16结论成立；-------------------------------12分 1 2 1 2 ②0x 4x ，则h(x)=h(x )=0 1 2 1 2 16 设H(x)=h(x)−h ，  x  16 16 1 16 此时H(x)=h(x)−h =g( )−g(x)=(a− )( −x)，-------------------14分  x  x a x 16 0x 4得到H(x)0，也即h(x )h ， 1 1 1  x  1 16 h(x )=h(x )=0，h(x )h ，----------------------------15分 1 2 2  x  1 16 x 4, 4， 2 x 1 16 由h(x)在(4,+)上单调递减，得到x  ，xx 16,得证.----------------------17分 2 x 1 2 1 第 4页 共 4页