文档内容
绵阳南山中学 2024 年秋季高 2023 级半期考试
数学试题参考答案
一、选择题
题 号 1 2 3 4 5 6 7 8 9 10 11
选 项 A A B C C D C D ABC AD ACD
三、填空题
12. 9 13. 14.
四、解答题
15.解:(Ⅰ)法一:因为AB边所在直线的方程为 ,所以 .又因为
矩形ABCD中, ,所以 ,所以由点斜式可得AD边所在直线的方程
为: ,即 ;
法二:因为 ,设AD边所在直线的方程为:
又因为直线AD过点 ,所以将点 代入上式得: .所以AD边所在
直线的方程为: ;
(Ⅱ)由 ,得: ,得AC所在直线的方程: ,即
.
16. 解 : ( Ⅰ ) 由 题 可 设 圆 C 的 方 程 为 , 则 有
,解得 ;所以圆C的标准方程为: ;
(Ⅱ)因为 ,所以过 的切线有两条,当 斜率存在时,设切线方程为:
即 ,所以有: ,解得: ;
第 1 页 共 6 页所以 的方程为: 。
第 2 页 共 6 页17.解:(Ⅰ)因为四边形 为正方形, 底面
,所以 , , 两两相互垂直,
如图,以A为原点,分别以 , , 方向为x轴、
y轴、z轴正方向建立空间直角坐标系 ,由题意可
得 A(0,0,0), , , , , , ,
, ,
则 , ,
设平面 的一个法向量为⃗n =(x ,y ,z ),则 ,
1 1 1 1
故 ,即 ,则 ,
令 ,得 ,
所以 ,
所以 ,又 平面 ,所以 平面 .
(Ⅱ)由(1)得直线 的一个方向向量为
平面 的一个法向量为 ,设直线 与平面 所成角为 ,
则
所以直线 与平面 所成角的正弦值为 .
18.解:(Ⅰ)由已知 ,所以C的标准方程为:
;
第 3 页 共 6 页Ⅱ ) 设 , 则 有 两 式 相 减 可 得 :
(
即 ,
即 ,为定值;
(Ⅲ)设 的方程为: , ,
由 消去 得:
,
令 , ,当且仅当
时,取“=”,所以 面积的最大值为1.
19.解:(Ⅰ)因为点P为圆A的“黄金点”,所以 ,即 ,
所以点P的轨迹是以A为圆心, 为半径的圆,故点P轨迹方程为
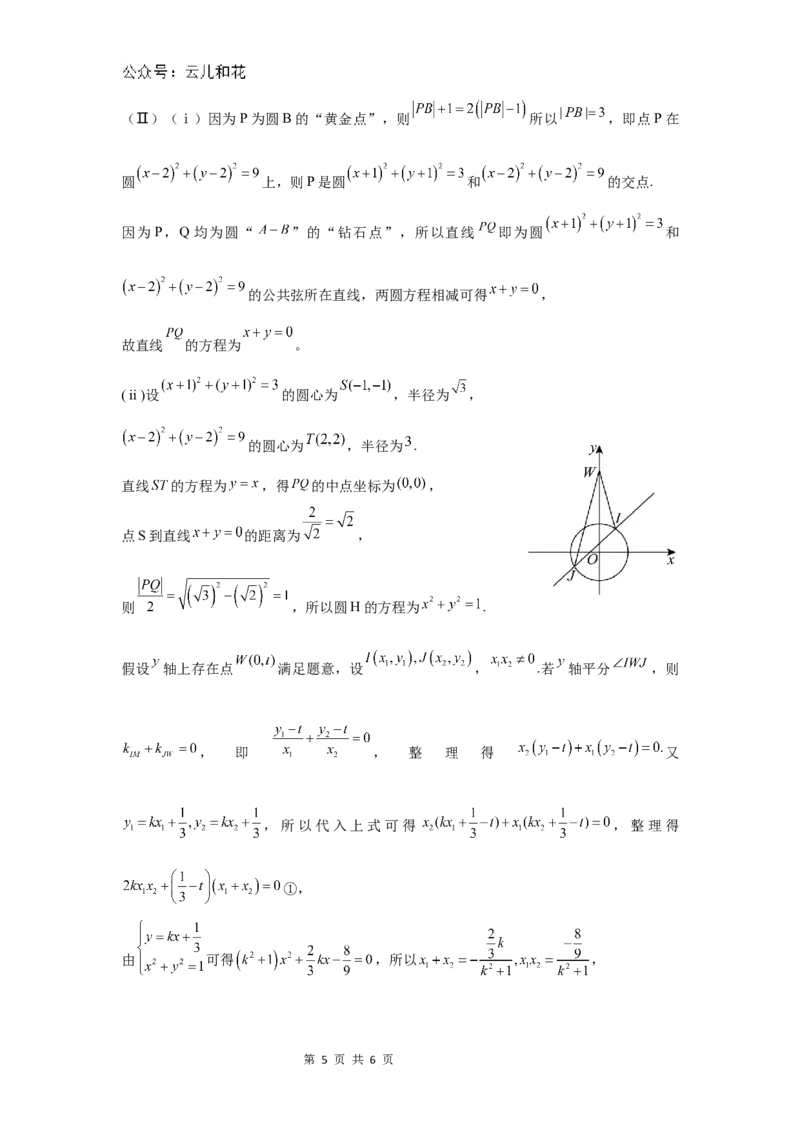
第 4 页 共 6 页(Ⅱ)(ⅰ)因为P为圆B的“黄金点”,则 所以 ,即点P在
圆 上,则P是圆 和 的交点.
因为 P,Q 均为圆“ ”的“钻石点”,所以直线 即为圆 和
的公共弦所在直线,两圆方程相减可得 ,
故直线 的方程为 。
( ii )设 的圆心为 ,半径为 ,
的圆心为 ,半径为 .
直线 的方程为 ,得 的中点坐标为 ,
点S到直线 的距离为 ,
则 ,所以圆H的方程为 .
假设 轴上存在点 满足题意,设 , .若 轴平分 ,则
, 即 , 整 理 得 又
,所以代入上式可得 ,整理得
①,
由 可得 ,所以 ,
第 5 页 共 6 页代入①并整理得 ,此式对任意的 都成立,所以 .故 轴上存在点
,使得 轴平分 .
第 6 页 共 6 页