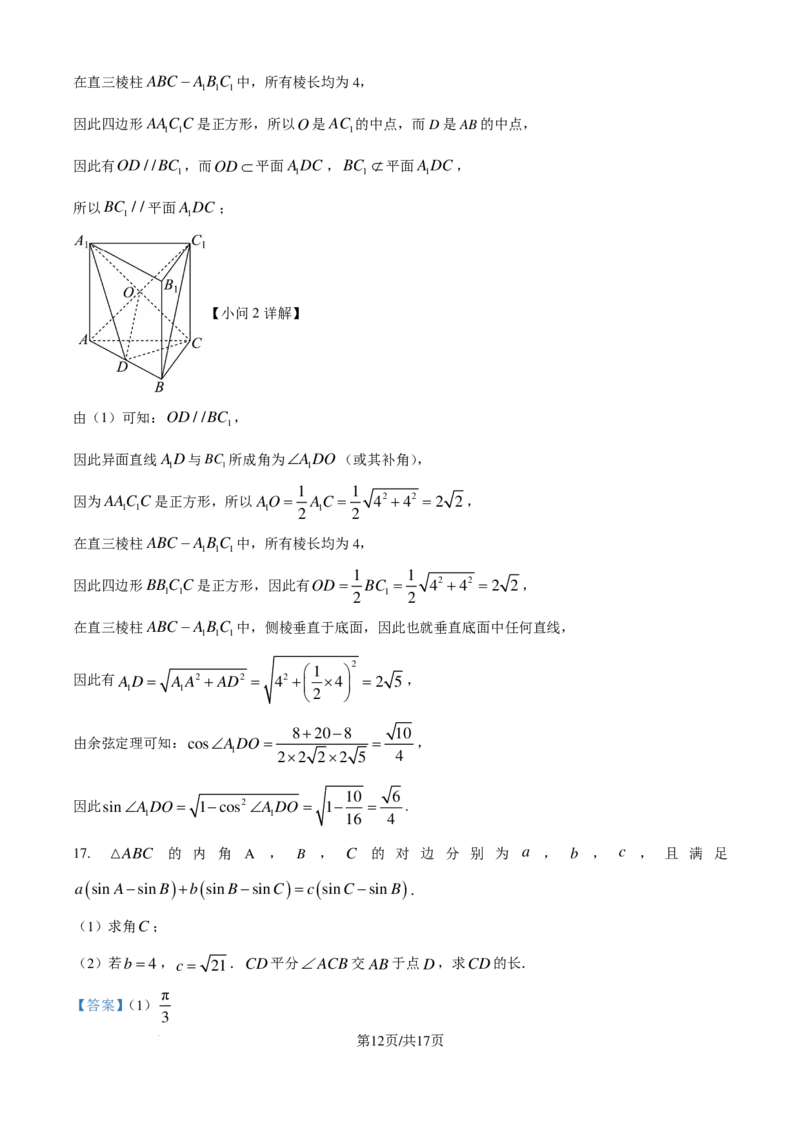
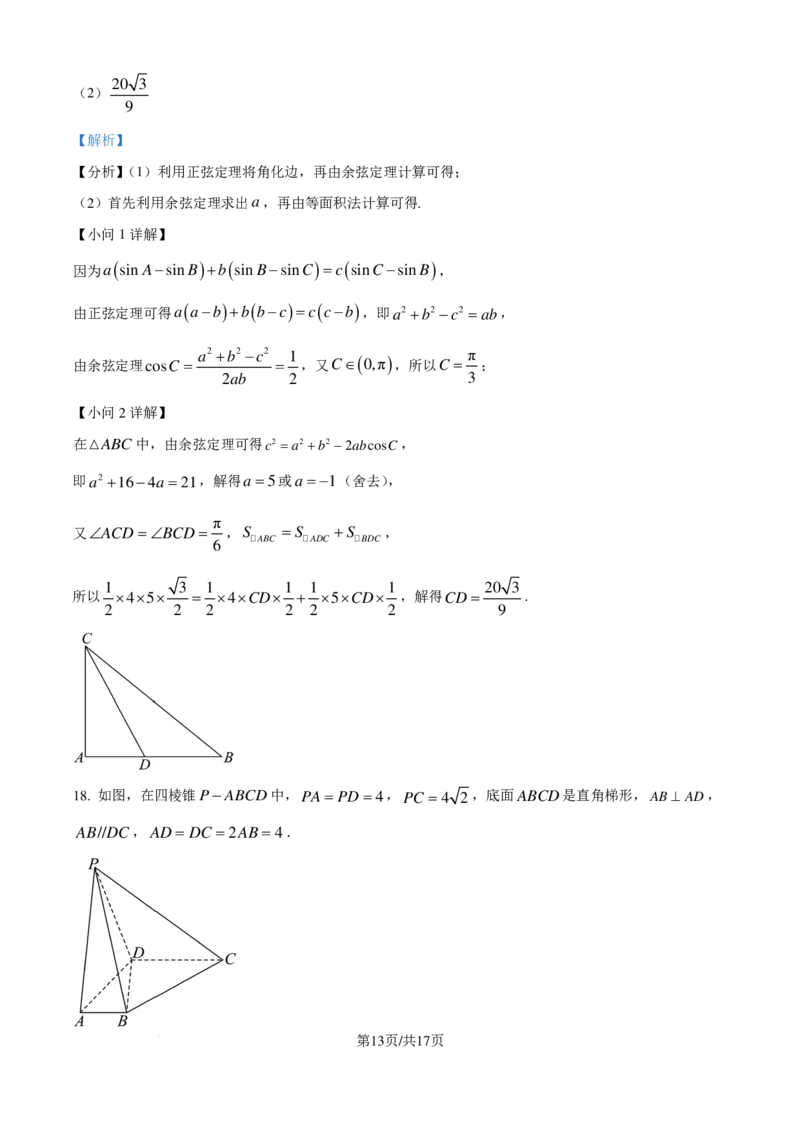
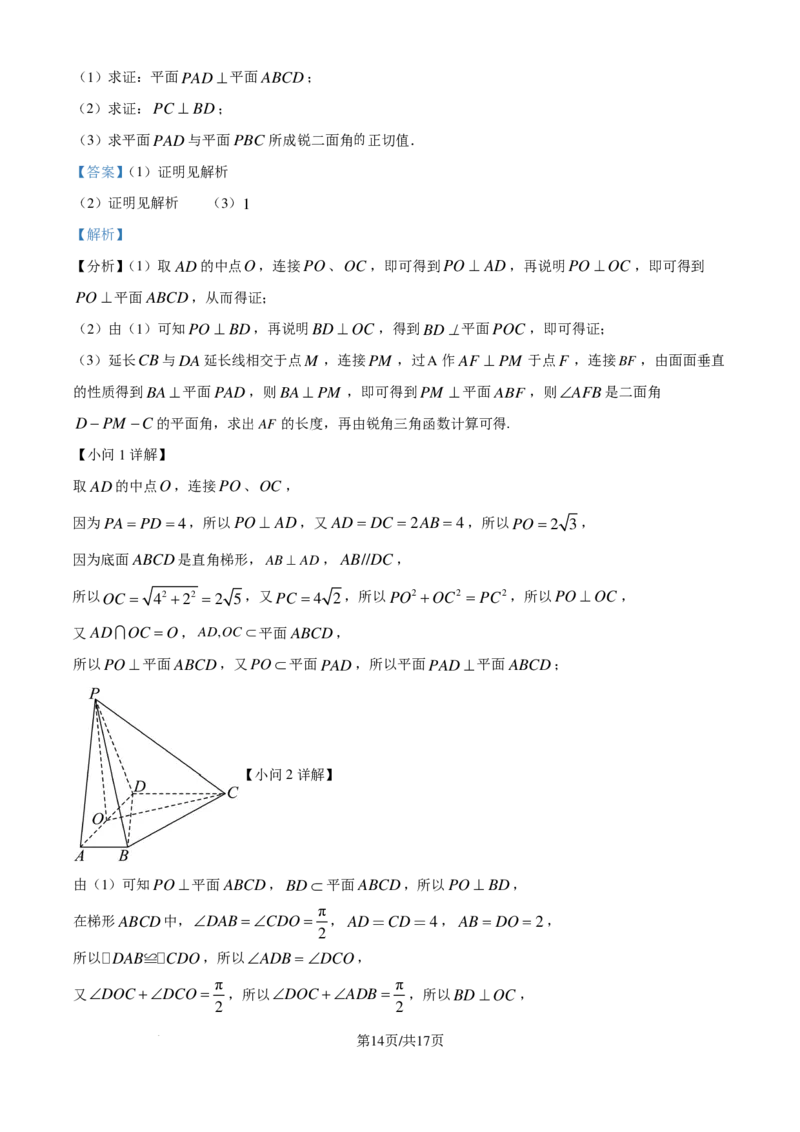
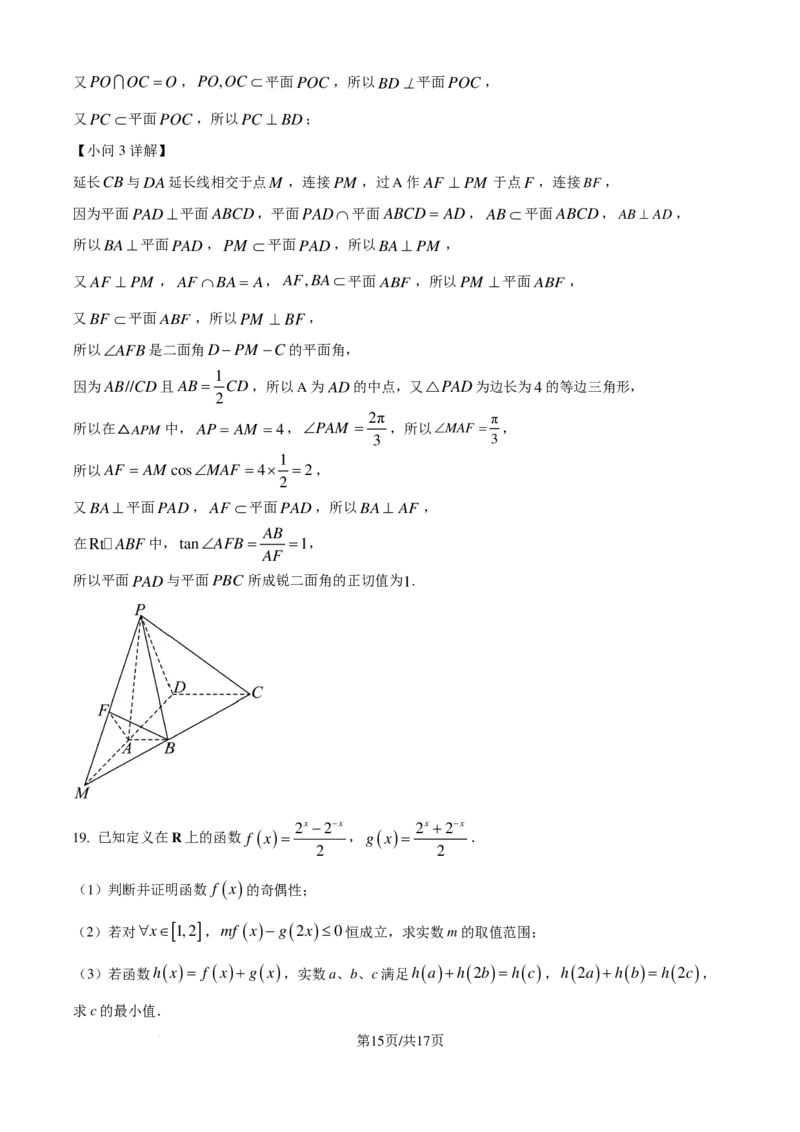
文档内容
高二数学
满分:150分 考试时间:120分钟
注意事项:
1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在考生信息条
形码粘贴区.
2.选择题必须使用 2B铅笔填涂;非选择题必须使用 0.5毫米黑色字迹签字笔书写,字体工
整、笔迹清晰.
3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在
草稿纸、试卷上答题无效.
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑.
5.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀.
一、选择题:本题共 8小题,每小题 5分,共 40分.在每小题给出的四个选项中,只有一项
是符合题目要求的.
{ } { }
A= x −1≤ x≤4 B= x lnx<2 AB =
1. 已知集合 , ,则 ( )
A. { x −1≤ x≤4 } B. { x 0< x2 D. a>4
【答案】A
【解析】
【分析】根据复合函数单调性的性质,结合指数函数和二次函数的单调性进行求解即可.
【详解】因为函数y =3x是实数集上的增函数,y =3x2−ax+1在区间 ( 1,2 ) 上单调递增,
所以函数y = x2 −ax+1在区间 ( 1,2 ) 上也是单调递增,
a
因为二次函数y = x2 −ax+1的对称轴为x= ,
2
a
所以有 ≤1,即a≤2,
2
故选:A
6. 正六边形六个顶点中任取四个点,构成等腰梯形的概率是( )
1 1 1 2
A. B. C. D.
10 5 3 5
【答案】D
【解析】
【分析】根据组合的定义,结合正六边形和等腰梯形的性质、古典概型运算公式进行求解即可.
【详解】正六边形六个顶点中任取四个点,不同的方法共有C4 =15种方法,
6
在如图所示正六边形AA A A A A 中,
1 2 3 4 5 6
显然四边形AA A A 、A A A A 、A A A A 、 A A A A 、A A AA 、A AA A 是等腰梯形,共6
1 2 3 6 2 3 4 1 3 4 5 1 4 5 6 3 5 6 1 4 6 1 2 5
个,
6 2
因此正六边形六个顶点中任取四个点,构成等腰梯形的概率是 = ,
15 5
故选:D
第3页/共17页
学科网(北京)股份有限公司7. f ( x ) 是定义在R上的函数,若 f ( 0 )=1,且对任意x∈R,满足 f ( x+2 )≤ f ( x )+2,
f ( x+8 )≥ f ( x )+8,则 f ( 2024 )=( )
A. 2023 B. 2024 C. 2025 D. 2026
【答案】C
【解析】
【 分 析 】首 先 推 导 出 f ( x+8 )− f ( x )≤8 , 从 而 得 到 f ( x+8 )− f ( x )=8 , 再 根 据
f ( 2024 )=
f ( 2024 )− f ( 2016 )
+
f ( 2016 )− f ( 2008 )
++
f ( 8 )− f ( 0 )
+ f ( 0 ) 计算可得.
【详解】因为 f ( x+2 )≤ f ( x )+2,即 f ( x+2 )− f ( x )≤2,
所以 f ( x+8 )− f ( x )=
f ( x+8 )− f ( x+6 )
+
f ( x+6 )− f ( x+4 )
+
f ( x+4 )− f ( x+2 )
+
f ( x+2 )− f ( x )
≤2+2+2+2=8,
又 f ( x+8 )≥ f ( x )+8,所以 f ( x+8 )− f ( x )=8,
所以 f
(
2024
)=f (
2024
)−
f
(
2016
)+f (
2016
)−
f
(
2008
)++f (
8
)−
f
(
0
)+
f
(
0
)
=253×8+1=2025.
故选:C
1 1 24
+ =
8. 已知 α α 7 ,α∈( 0,π ) ,则cos2α=( )
sin cos
2 2
17 17 79 79
A. B. − C. D. −
81 81 128 128
【答案】B
【解析】
【分析】先对式子进行化简求出sinα,再根据二倍角公式即可求解.
1 1 24
+ =
【详解】解: α α 7 ,
sin cos
2 2
第4页/共17页
学科网(北京)股份有限公司α α
cos +sin
24
2 2
即 = ,
α α 7
sin cos
2 2
α α
cos +sin
24
2 2
即 = ,
1 7
sinα
2
α α 2
cos +sin 12 2
2 2
即 = ,
sinα 7
1+sinα 144
即 = ,
sin2α 49
即144sin2α−49sinα−49=0,
即 ( 16sinα+7 )( 9sinα−7 )=0,
又α∈(
0,π
)
,
7 7
解得:sinα= ,sinα=− (舍),
9 16
2
7 17
cos2α=1−2sin2α=1−2× =− .
9 81
故选:B.
二、选择题:本题共 3小题,每小题 6分,共 18分.在每小题给出的选项中,有多项符合题
目要求.全部选对的得 6分,部分选对的得部分分,有选错的得 0分.
9. 对于随机事件A和事件B,P
(
A
)=0.3,P (
B
)=0.4,则下列说法正确的是(
)
A. 若A与B互斥,则P ( AB )=0.3 B. 若A与B互斥,则P ( A∪B )=0.7
C. 若A与B相互独立,则P ( AB )=0.12 D. 若A与B相互独立,则P ( A∪B )=0.7
【答案】BC
【解析】
【分析】根据互斥事件、相互独立事件的概率公式计算可得.
【详解】对于A:若A与B互斥,则P
(
AB
)=0,故A错误;
对于B:若A与B互斥,则P ( AB )= P ( A )+P ( B )=0.7,故B正确;
第5页/共17页
学科网(北京)股份有限公司对于C:若A与B相互独立,则P
(
AB
)=
P
(
A
)
P
(
B
)=0.12,故C正确;
对于D:若A与B相互独立,
则P ( A∪B )= P ( A )+P ( B )−P ( AB )=0.3+0.4−0.3×0.4=0.58,故D错误.
故选:BC
10. 已知正数a,b满足4a+b+ab=12,则下列结论正确的是( )
A. ab的最大值为4 B. 4a+b的最小值为8
1 1 3
C. a+b的最小值为3 D. + 的最小值
a+1 b 4
【答案】ABD
【解析】
【分析】利用基本不等式判断A、B;依题意可得 ( a+1 )( b+4 )=16,再由基本不等式判断C、D.
【详解】因为正数a,b满足4a+b+ab=12,
所以12−ab=4a+b≥2 4ab =4 ab,当且仅当4a=b,即a =1,b=4时等号成立,
解得0< ab ≤2,所以0