数学答案_2024-2025高二（7-7月题库）_2024年07月试卷_0702陕西省西安中学2023-2024学年高二下学期6月期末考试_陕西省西安中学2023-2024学年高二下学期6月期末考试数学

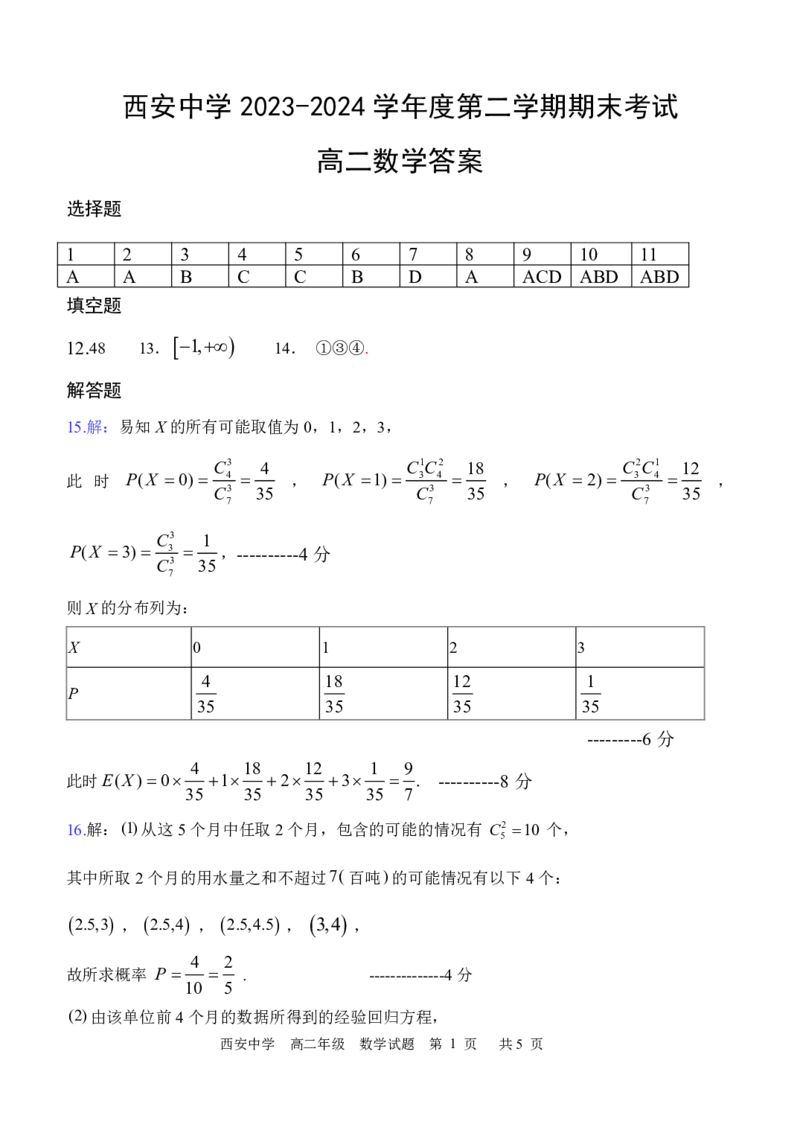
西安中学 2023-2024 学年度第二学期期末考试 高二数学答案 选择题 1 2 3 4 5 6 7 8 9 10 11 A A B C C B D A ACD ABD ABD 填空题 12.48 13． 1, 14． ①③④. 解答题 15.解：易知X的所有可能取值为0，1，2，3， C3 4 C1C2 18 C2C1 12 此 时 P(X 0) 4  ， P(X 1) 3 4  ， P(X  2) 3 4  ， C3 35 C3 35 C3 35 7 7 7 C3 1 P(X 3) 3  ，----------4 分 C3 35 7 则X的分布列为： X 0 1 2 3 4 18 12 1 P 35 35 35 35 ---------6 分 4 18 12 1 9 此时E(X)0 1 2 3  . ----------8 分 35 35 35 35 7 16.解：(1)从这5个月中任取2个月，包含的可能的情况有 C2 10 个， 5 其中所取2个月的用水量之和不超过7(百吨)的可能情况有以下4个： 2.5,3 ， 2.5,4 ， 2.5,4.5 ，  3,4  ， 4 2 故所求概率 P   . 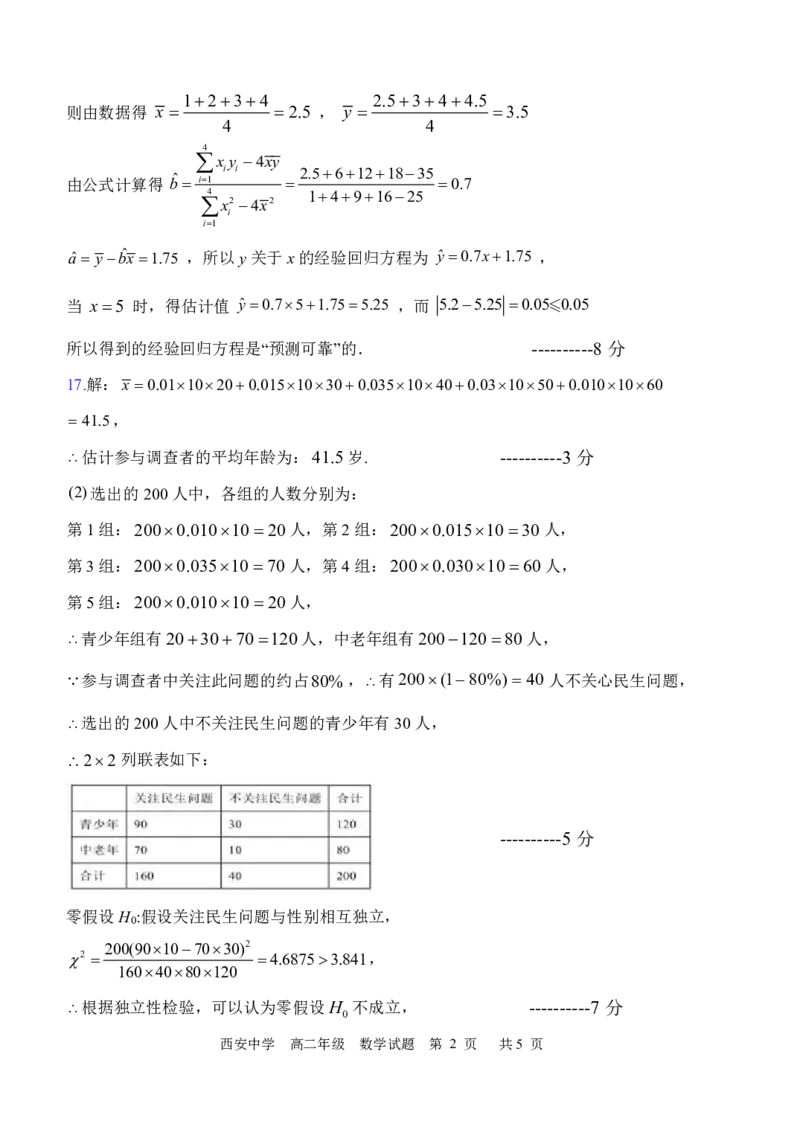--------------4分 10 5 (2)由该单位前4个月的数据所得到的经验回归方程， 西安中学 高二年级 数学试题 第 1 页 共5 页 {#{QQABZYiAogCgAJAAAAhCAQVoCgMQkAGAAYgGgFAAIAAAgQFABAA=}#}1234 2.5344.5 则由数据得 x  2.5 ， y  3.5 4 4 4 x y 4xy i i 2.56121835 由公式计算得 b ˆ i1  0.7 4 1491625 x2 4x2 i i1 aˆ yb ˆ x 1.75 ，所以y关于x的经验回归方程为 yˆ 0.7x1.75 ， 当 x5 时，得估计值 yˆ 0.751.755.25 ，而 5.25.25 0.05„0.05 所以得到的经验回归方程是“预测可靠”的． ----------8 分 17.解：x 0.0110200.01510300.03510400.0310500.0101060 41.5， 估计参与调查者的平均年龄为：41.5岁. ----------3 分 (2)选出的200人中，各组的人数分别为： 第1组：2000.0101020人，第2组：2000.0151030人， 第3组：2000.0351070人，第4组：2000.0301060人， 第5组：2000.0101020人， 青少年组有203070120人，中老年组有20012080人， 参与调查者中关注此问题的约占80%，有200(180%) 40 人不关心民生问题， 选出的200人中不关注民生问题的青少年有30人， 22列联表如下： ----------5 分 零假设H :假设关注民生问题与性别相互独立， 0 200(90107030)2 2  4.68753.841， 1604080120 根据独立性检验，可以认为零假设H 不成立， ----------7 分 0 西安中学 高二年级 数学试题 第 2 页 共5 页 {#{QQABZYiAogCgAJAAAAhCAQVoCgMQkAGAAYgGgFAAIAAAgQFABAA=}#}即能依据小概率值0.050的独立性检验，认为是否关注民生与年龄有关. 30 1 (3)由题意，青少年“不关注民生问题”的频率为  ，将频率视为概率，每个青少 120 4 1 年“不关注民生间题”的概率为 ， 4 1 因为每次抽取的结果是相互独立的，所以Y∽B(4, )， 4 1 1 P(Y k)Ck( )k(1 ) 4k，k 0，1，2，3，4 4 4 4 1 1 27 所以P(Y 2)C2( )2(1 )42  ， 4 4 4 128 1 E(Y)4 1. ----------10 分 4 18.解：(1)f(x) 的定义域为(0,)， 2 当a2时， f(x)x2 2lnx， f(x) 2x ，令 f(x) 0，得x1， x 当x(0,1)时， f(x) 0;当x(1,)时， f(x) 0， 所以 f(x)在(0,1)上单调递减，在(1,)上单调递增， 所以x1是 f(x)的极小值点， 又 f(1)12ln11，故 f(x)的极小值为1，无极大值； ----------4 分 (2)由g(x) f(x)(12a)xx2 alnx(12a)x得， a (2x1)(xa) g(x)2x (12a) ， x x 当a„0时，g(x)0，所以g(x)在(0,)上单调递增， 则g(x)最多有一个零点，不合题意; ----------6 分 当a0时，当x(0,a)时，g(x)0，当x(a,)时，g(x)0， 所以g(x)在(0,a)上单调递减，在(a,)上单调递增， x  0,g(x) ，x  ,g(x)  所以：g(x)的极小值为g(a)a2 alna(12a)aaalnaa2 a(1lnaa)0， ---8分 西安中学 高二年级 数学试题 第 3 页 共5 页 {#{QQABZYiAogCgAJAAAAhCAQVoCgMQkAGAAYgGgFAAIAAAgQFABAA=}#}令u(a)1lnaa，a0，则u(a)1lnaa0 1 u(a)1 0，所以u(a)在(0,)上单调递减， a 又u(1)1ln110， 当0 a„1时，u(a) 0，所以g(x)最多有一个零点，不合题意; 当a 1时，u(a) 0 ， 所以当a 1时，函数g(x)恰有两个零点， ----------10 分 综上，a的取值范围是(1,).   2 19.（1）记该顾客第i iN* 次摸球抽中奖品为事件A，依题意，P  ， 1 7 P  P  A  P  A  P  A |A P  A  P  A |A   2  1   1 2   1  19 . 2 2 1 2 1 1 2 1 7 3  7 2 42 107 P  3 252 ----------6 分 （2）因为P  A |A  1 ，P  A | A   1 ，P  P  A ， n n1 3 n n1 2 n n 所以P  A  P  A  P  A | A P  A  P  A | A  ， n n1 n n1 n1 n n1 1 1 1 1 所以P  P   1P  P  ， n 3 n1 2 n1 6 n1 2 3 1 3 所以P   P   ， ----------8 分 n 7 6 n1 7 2 3 1 又因为P  ，则P    0， 1 7 1 7 7  3 1 1 所以数列P  是首项为 ，公比为 的等比数列，  n 7 7 6 n1 3 1 1 故P      .…………………………………10分 n 7 7 6 西安中学 高二年级 数学试题 第 4 页 共5 页 {#{QQABZYiAogCgAJAAAAhCAQVoCgMQkAGAAYgGgFAAIAAAgQFABAA=}#}3 1 3 19 证明：当 n为奇数时，P     ， n 7 76n1 7 42 3 1 当n 为偶数时，P   ，则P 随着n的增大而减小， n 7 76n1 n 19 所以，P  P  . n 2 42 综上，该顾客第二次摸球抽中奖品的概率最大.…………………………………12分 西安中学 高二年级 数学试题 第 5 页 共5 页 {#{QQABZYiAogCgAJAAAAhCAQVoCgMQkAGAAYgGgFAAIAAAgQFABAA=}#}