数学答案_2024-2025高二（7-7月题库）_2024年07月试卷_0707江西省上饶市2023-2024学年高二下学期期末教学质量检测_江西省上饶市2023-2024学年高二下学期期末教学质量检测数学

上饶市2023-2024学年高二下学期期末考试数学参考答案 1 2 3 4 5 6 7 8 9 10 11 C C B C A D C C BC ACD BD 12: 12 13： ln2 14：1011 a 15解：（1）定义域为0,， fx 2bx7，-----------------------------------2分 x 将点  1, f 1 代入2xy30中， 21 f 130，∴ f 15.  1 a2 f 1b7 5   2   3  f1a2b72  b 2 ------------------------------------------------------------6分 3 1 （2） f x2lnx x27x ， 2 2 2 23x27 x23x1 fx 3x7  x x x ，------------------------------------------8分  1 1 1  x 0,   ,2 2 2,  3 3 3  fx ＋ 0 － 0 ＋ f x  极大值  极小值   1 1  f x的单调递增区间为0, ，2,，单调递减区间为 ,2；-----------------------11分  3 3  1 5 15 f x 的极大值为 f  3    3 2ln3 ，极小值为 f 2 2 2ln2 .-----------------------13分 16 解：（1）x＞1，y＝ ≥ +1＝3，--------------------5分 当且仅当x﹣1＝ ，即x＝2时，等号成立，则函数 的最小值为3； -------------------------------------------------------------------------------------------------------------7分 （2）∵ ， 1 学科网（北京）股份有限公司∴1﹣3x＞0，∴ ，----------12分 当且仅当3x＝1﹣3x，即 时，等号成立，故当 时，y取得最大值 ．----15分 17解：（Ⅰ）当 n＝1时， ，得a1 ＝1，---------------------------------------2分 当n≥2时， ，得 an ＝3an﹣1 ， ∴数列{an}是公比为3的等比数列， ∴ ．----------------------------------------------------------------------------------------6分 （Ⅱ）由（Ⅰ）得： ，又 ① ∴ ② 两式相减得： ，--------------------------12分 故 ， ∴ ．---------------------------------------------------------------------------15分 1 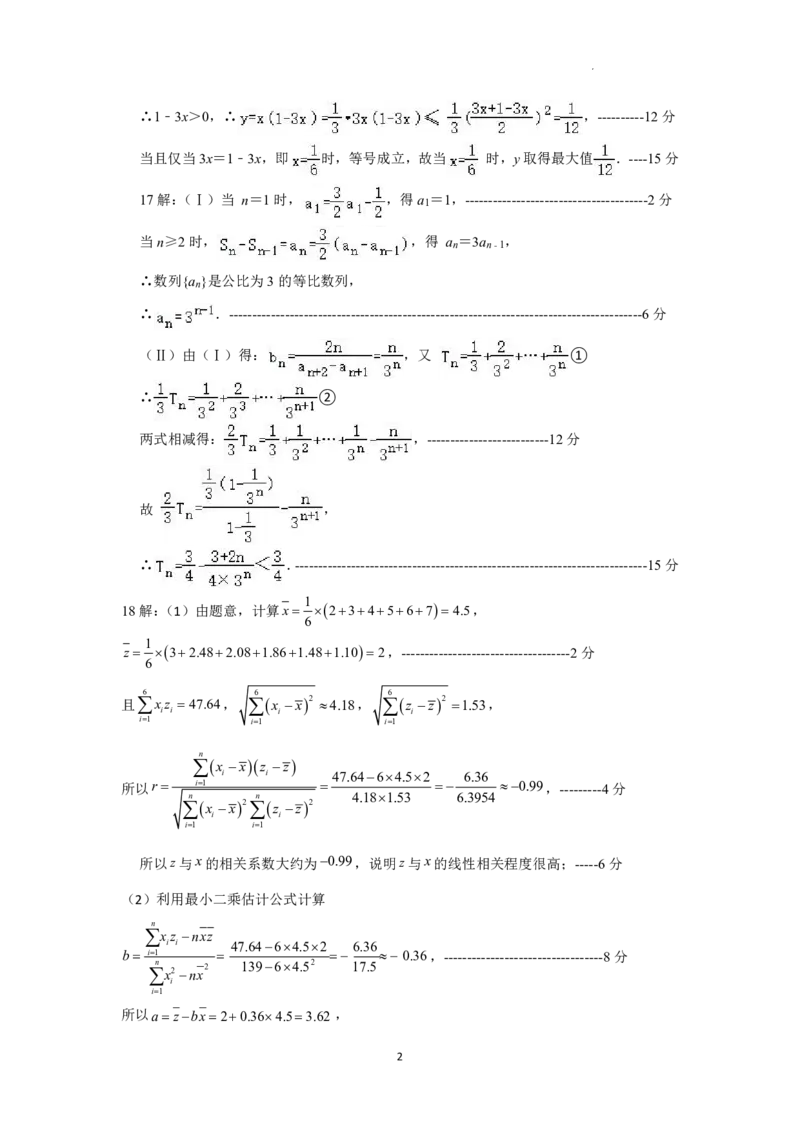18解：（1）由题意，计算x 2345674.5， 6 1 z 32.482.081.861.481.102，------------------------------------2分 6 6 6 6 且xz 47.64， x x2 4.18， z z2 1.53， i i i i i1 i1 i1 n x xz z i i 47.6464.52 6.36 所以r i1   0.99，---------4分 n n 4.181.53 6.3954 x x2z z2 i i i1 i1 所以z与x的相关系数大约为0.99，说明z与x的线性相关程度很高；-----6分 （2）利用最小二乘估计公式计算 n xz nxz i i 47.6464.52 6.36 b i1    0.36，----------------------------------8分  n x2nx 2 13964.52 17.5 i i1 所以azbx 20.364.53.62 ， 2 学科网（北京）股份有限公司所以z关于x的线性回归方程是z0.36x3.62， 又zlny，所以y关于x的回归方程是ye0.36x3.62.------------------------------------10分 令x9，解得ye0.3693.62 1.46，即预测某辆A型号二手车当使用年数为9年时售价约 1.46万元；----------------------------------------------------------------------------------------12分 （3）当y0.7118时，e0.36x3.62 0.7118eln0.7118 e0.34，-------------------------------15分 所以0.36x3.620.34，解得x11，因此预测在收购该型号二手车时车辆的使用年数 不得超过11年．----------------------------------------------------------------------------------17分 19【解答】解：（1）f（x）定义域为（0，+∞）， ，--------------------------------------2分 对于方程x2+（2﹣2a）x+1＝0，Δ＝（2﹣2a）2﹣4＝4（a2﹣2a）， 当Δ≤0，即0≤a≤2时，x2+（2﹣2a）x+1≥0，f′（x）≥0，f（x）在（0，+∞）上单 增， --------------------------------------3分 当Δ＞0，即a＜0或a＞2时，方程x2+（2﹣2a）x+1＝0有两不等根， ， ，而x1+x2 ＝2（a﹣1），x1x2 ＝1， 所以当a＜0时，x1 ＜x2 ＜0，f′（x）＞0在（0，+∞）上恒成立，f（x）在（0，+∞） 上单增； 当a＞2时，0＜x1 ＜x2 ，x （0，x1 ）或x （x2 ，+∞）时，f′（x）＞0，x （x1 ，x2 ）时， f′（x）＜0， ∈ ∈ ∈ 所以f（x）在（0，x1 ）和（x2 ，+∞）上单增，在（x1 ，x2 ）上单减， 综上，当a≤2时，f（x）在（0，+∞）上单增； 当a＞2时，f（x）在 和 上单增， 在 上单减；-----------------------------------------5分 （2） 3 学科网（北京）股份有限公司＝ ＝ ，-------------------------------------------------8分 所以要证 ，即证 ，即证 ， 也即证 （*）成立． 设 ，函数 ，由（1）知h（t）在（0，+∞）上 单增，且h（1）＝0， 所以t （0，1）时，h（t）＜0，所以（*）成立，原不等式得证；-----------------10分 ∈ （3）由题可得 ，-----------------------------11分 因为99×81＝902﹣92＜902，98×82＝902﹣82＜902，…，91×89＝902﹣12＜902， 所以 ， -----------------------------13分 又由（2）知t （1，+∞）， ， ∈ 取 ，有 ， -----------------------------15分 即 ，即 ， 所以 ．-----------------------------------------------------------------------17分 4 学科网（北京）股份有限公司