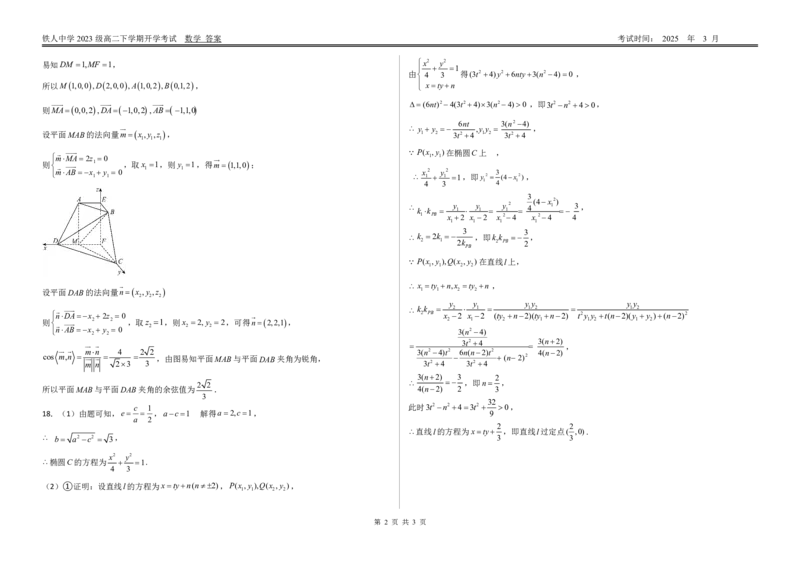数学答案_2024-2025高二（7-7月题库）_2025年03月试卷_0316黑龙江省大庆铁人中学2024-2025学年高二下学期开学考试

铁人中学2023级高二下学期开学考试 数学 答案 考试时间： 2025 年 3 月
铁人中学 2023 级高二下学期开学考试 因为a a 2，所以aq2 aq2，即q2q20，解得q=2或q  1（舍），
3 2 1 1
数学答案 所以a aqn1 2n1，
n 1
一 选择题 设b 的公差为d，
n
1 2 3 4 5 6 7 8 9 10 11 因为a b b ，a b 2b ，所以b b 8，b 2b 16，
4 3 5 5 4 6 3 5 4 6
C C A A D B D A BC BD BCD
2b 6d 8
所以 1 ，解得d b 1，所以b b (n1)d n.
二 填空题 3b 13d 16 1 n 1
1
 n1 a 2n1 1 1
32 2 2,n为奇数 （2）c  n    ，
12. x y30. 13.2 172 14.a n  n n a n 1a n1 1 (2n11)(2n1) 2n11 2n1
 1
322 1,n为偶数
1 1 1 1 1 1 1 1
所以T c c c Lc       L 
n 1 2 3 n 201 211 211 221 221 231 2n11 2n 1
三 解答题
1 1
  ， 因为n为正整数，所以 >0，所以 <
2 2n 1
1 1
15.（1）由题意得2c2 6，即c 6，所以a2b2 6，
2  +1   2
又因为数列 单调递减，所以 单调递增，所以 =
因为双曲线C经过点2,2，所以代入可得 a 4 2  b 4 2 1， 2  1 +1     ≥  1 1 6
所以
解得a2 2，b2 4， 1 1
17．（6≤ 1）   由 < 题2意知在等腰梯形ABCD中，AB//CD，
x2 y2
所以C的方程为  1.
2 4 又E,F分别为AB,CD的中点，所以EF  AB,EF CD，
（2）设直线l的方程为ykxmm0，Ax,y ，Bx ,y ，AB的中点为Mx ,y  . 即折叠后EF DF,EF CF ，
1 1 2 2 0 0
ykxm DFCF F ，所以EF 平面DCF，
联立  x2 y2 ，消去y整理得：  2k2 x22kmx  m24  0，
  1 又MC 平面DCF，
 2 4
所以2km24  2k2 m24  8  m22k24  0，x x  2km ， 所以EF MC．
1 2 2k2
（2）∵平面BEFC平面AEFD，平面BEFC平面AEFDEF ，且EF DF，
x x km 2m  km 2m 
则x  1 2  ，y kx m ，所以M , .
0 2 2k2 0 0 2k2 2k2 2k2  所以DF平面BEFC，CF 平面BEFC,
2m km 1
因为M在直线y4x上，所以 4· ，又m0，所以k  . DF CF，DF,EF,CF两两垂直，
2k2 2k2 2
16．（1）设a 的公比为q0，
以F 为坐标原点，分别以FD,FC,FE所在直线为x,y,z轴，建立空间直角坐标系，
n
第 1 页 共 3 页铁人中学2023级高二下学期开学考试 数学 答案 考试时间： 2025 年 3 月
易知DM 1,MF 1， x2 y2
  1
由 4 3 得(3t24)y26nty3(n24)0 ，
所以M1,0,0,D2,0,0,A1,0,2,B0,1,2，   xtyn
   (6nt)24(3t24)3(n24)0 ，即3t2n240，
则MA0,0,2,DA1,0,2,AB 1,1,0
6nt 3(n24)
  y y  ,y y  ，
设平面MAB的法向量mx,y,z ， 1 2 3t24 1 2 3t24
1 1 1
  P(x,y )在椭圆C上 ，
 mMA2z 0 ur 1 1
则 m    A  B  x
1
1 y
1
 0 ，取x 1 1，则y 1 1，得m1,1,0；

x
1
2

y
1
2
1，即y2 
3
(4x2)，
4 3 1 4 1
3
(4x2)
 y y y 2 4 1 3，
k k  1  1  1  
1 PB x 2 x 2 x 24 x 24 4
1 1 1 1
3 3
k 2k  ，即k k  ，
2 1 2k 2 PB 2
PB
P(x,y ),Q(x ,y )在直线l上，
1 1 2 2
 x ty n,x ty n ，
设平面DAB的法向量nx ,y ,z  1 1 2 2
2 2 2
y y y y y y
 n  D  A  x 2z  0 r k 2 k PB  x  2 2  x  1 2  (ty n2 1 )(t 2 y n2)  t2y y t(n2)( 1 y 2 y )(n2)2
则   2 2 ，取z 2 1，则x 2 2,y 2 2，可得n2,2,1， 2 1 2 1 1 2 1 2
nABx y  0 3(n24)
2 2
  
3t24

3(n2)
，
  mn 4 2 2 3(n24)t2 6n(n2)t2 4(n2)
cos m,n      ，由图易知平面MAB与平面DAB夹角为锐角，  (n2)2
m n 23 3 3t24 3t24
3(n2) 3 2
2 2
  ，即n ，
所以平面MAB与平面DAB夹角的余弦值为 ． 4(n2) 2 3
3
32
c 1 此时3t2n243t2 0，
18．（1）由题可知，e  ，ac1 解得a2,c1， 9
a 2
2 2
直线l的方程为xty ，即直线l过定点( ,0).
 b a2c2  3 ， 3 3
x2 y2
椭圆C的方程为  1.
4 3
（2）①证明：设直线l的方程为xtyn(n2)，P(x,y ),Q(x ,y )，
1 1 2 2
第 2 页 共 3 页铁人中学2023级高二下学期开学考试 数学 答案 考试时间： 2025 年 3 月
由a a 2n1，
n1 n
1
可得a a a a a a ...a a 135...2n1 n12n1n2，
n 1 2 1 3 2 n n1 2
上式对n1也成立，即有a n2，nN*；
n
（2）（i）若a 5，且满足b c 2a 4，可得b b b b a a 2a 4，
1 n1 n n n1 n1 n n n1 n n
2
②解：记直线l过定点N( ,0)，
3
即a 3a 4，即有a 23a 2，
n1 n n1 n
8
 A(2,0) |AN| ，
3
可得数列a 2是首项和公比均为3的等比数列，即有a 23n，即a 23n，
1 4 n n n
S  |AN||y y | (y y )24y y ，
2 1 2 3 1 2 1 2
可得b a a 23n，c b b 23n123n 43n，不为非零常数，故a 不为二阶等差
n n1 n n n1 n n
4t 32 1
y y  ,y y   ，
1 2 3t24 1 2 3 3t24 数列；
1 4 16 3 27t232
 S  |AN|| y y | (y  y )24y y 
2 1 2 3 1 2 1 2 27t236 （ii）数列a n 的前n项和 S 2n 3  13n 2n 1 3n13 ，
1 n 13 2
16 3
4 ，
27t232
114n
27t232 不等式3n2S 4a 0，即13n4n110，即为1 对nN*恒成立．
n n 3n
16 3
S  114n 74n 114n 8n26
令m 27t2 32[4 2,)，则 4 ， 设d  ，d d    ，
m n 3n n1 n 3n1 3n 3n1
m
4 当1n3时，d d d d ，当d 4时，可得d d 0，即有d d ...d ，
m 在[4 2,)上单调递增， 4 3 2 1 n1 n 4 5 n
m
5
16 3  16 6
可得数列d
n
中最小项为d
4

81
，
当m4 2时，S有最大值 4 9 .
4 2 5 76
4 2 则1 ，即有 ，则实数的取值范围（- ， ）
81 81
76
19．（1）若a 1，b 3，c 2， ∞ −81
1 1 n
则a a a 13，即a 4，
2 1 2 2
由c b b 2，可得b 32n12n1，
n n1 n n
则a a b 5，可得a 9，a a b  7，解得a 16，
3 2 2 3 4 3 3 4
第 3 页 共 3 页