文档内容
射洪中学高 2022 级高二(下)期末模拟考试
数学试题
(考试时间:120分钟 满分:150分)
注意事项:
1.答卷前,考生务必将自己的班级、姓名、考号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂
黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。写在本试卷上无效。
3.回答非选择题时,将答案写在答题卡对应题号的位置上。写在本试卷上无效。
4.考试结束后,将答题卡交回。
第 I 卷(选择题)
一、单选题:本大题共8小题,每小题5分,共40分
1.下列求导数运算中正确的是( )
A. B.
C. D.
2.某集团从人事部选取5人,市场部选取10人组成服务队,为了进一步开展工作,现选取2
人作为队长,则2位队长都来自同一部门的前提下,2位队长全部来自市场部的概率为(
).
A. B. C. D.
3.已知随机变量 服从正态分布 ,且 ,则 ( )
A. B. C. D.
4.已知函数 ,则 在( )
A. 上单调递增 B. 处有最小值
C. 上有三个零点 D. 上单调递增
5.对于数据组 ,如果由线性回归方程得到的自变量 的估计值是 ,那么将
称为样本点 处的残差.某商场为了给一种新商品进行合理定价,将该商品按事先
拟定的价格进行试销,得到表所示数据.若销量 (单位:件)与单价 (单位:元)之间的线
性回归方程为 ,且样本点 处的残差为3,则 ( )
单价 /元 8.2 8.4 8.6 8.8
销量
84 83 78 m
件
A.65 B.67 C.73 D.75
6.2024年中国足球乙级联赛陕西联合的主场火爆,一票难求,主办方设定了三种不同的票
价分别对应球场三个不同的区域,五位球迷相约看球赛,则五人中恰有三人在同一区域的
不同座位方式共有( )
A.30种 B.60种 C.120种 D.240种
高二数学 第 1 页 共 5 页7.已知随机变量 的分布列如下:
2 3 6
则 的值为( )
A.20 B.18 C.8 D.6
8.若对任意的 且 ,则实数m的取值范围是
( )
A. B. C. D.
二、多选题:本大题共3小题,每小题6分,共18分。在每小题给出的四个选项中,有多
项符合题目要求,全部选对的得6分,部分选对得3分,有选错的得0分.
9.有3台车床加工同一型号的零件,第1台加工的次品率为6%,第2,3台加工的次品率均
为5%,加工出来的零件混放在一起.已知第1,2,3台车床加工的零件数分别占总数的
25%,30%,45%,则下列说法中正确的有( )
A.任取一个零件,它是次品的概率是0.0525
B.任取一个零件,它是次品的概率是0.16
C.如果取到的零件是次品,则它是第1台车床加工的概率为
D.如果要求加工次品的操作员承担相应的责任,那么第1台车床的操作员应承担的份额
小于第2台车床的操作员应承担的份额
10.已知 ,则下列命题正确的是
( )
A. ;
B. ;
C.
D. .
11.已知函数 ( 且 ),则( )
A.当 时,曲线 在点 处的切线方程为
B.函数 恒有1个极值点
C.若曲线 有两条过原点的切线,则
D.若 有两个零点,则
第 II 卷(非选择题)
三、填空题:本大题共3小题,每小题5分,共15分.
12.已知随机变量 服从两点分布,且 ,设 ,那么 .
13.若一个三位数的各位数字之和为10,则称这个三位数为“十全十美数”,如 都是
高二数学 第 2 页 共 5 页“十全十美数”,则一共有 个“十全十美数”.
14.若函数 存在唯一极值点,则实数 的取值范围是 .
四、解答题:本题共5小题,解答应写出文字说明、证明过程或演算步骤.
15.(13分)2023年秋季,支原体肺炎在我国各地流行,该疾病的主要感染群体为青少年和老
年人.某市医院传染病科从该市各医院某段时间就医且年龄在70岁以上的老年人中随机抽查
了200人,并调查其患病情况,将调查结果整理如下:
没有慢性疾
有慢性疾病 合计
病
未感染支原体肺
40 80
炎
感染支原体肺炎 40
合计 120 200
(1)完成 列联表,并根据小概率值 的独立性检验,分析70岁以上老年人感染
支原体肺炎与自身慢性疾病是否有关?
(2)用样本估计总体,并用本次抽查中样本的频率代替概率,从本省各医院某段时间就
医且年龄在70岁以上的老年人中随机抽取3人,设抽取的3人中感染支原体肺炎的人数为
X,求X的分布列,数学期望 和方差 .
附: , .
0.10 0.05 0.025 0.010 0.001
2.706 3.841 5.024 6.635 10.828
▲
16.(15分)(1)已知 的展开式中共有7项.求展开式中的常数项;
(2)已知 , , 的展开式中含 项的系数为 ,含
项的系数为 ,求 的近似值.(精确到0.01)
▲
17.(15分)已知函数 .
高二数学 第 3 页 共 5 页(1)求函数 的单调区间和极值;
(2)若不等式 在 上恒成立,求实数 的取值范围.
▲
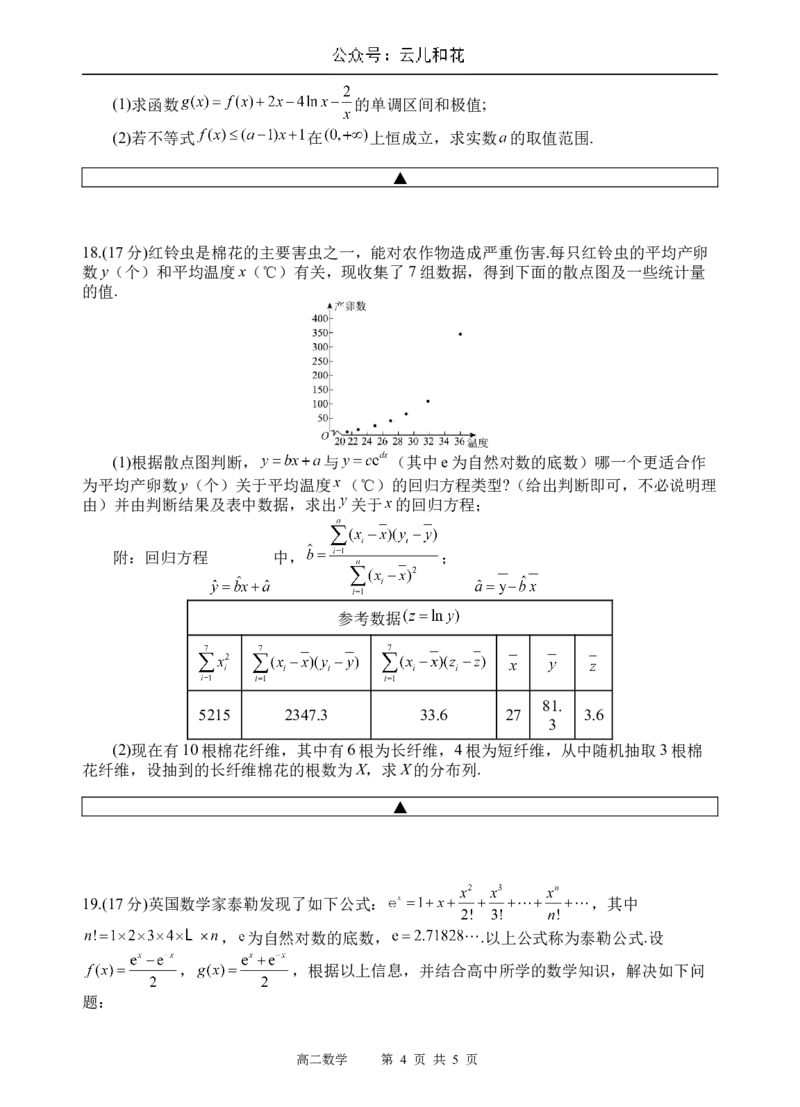
18.(17分)红铃虫是棉花的主要害虫之一,能对农作物造成严重伤害.每只红铃虫的平均产卵
数y(个)和平均温度x(℃)有关,现收集了7组数据,得到下面的散点图及一些统计量
的值.
(1)根据散点图判断, 与 (其中e为自然对数的底数)哪一个更适合作
为平均产卵数y(个)关于平均温度 (℃)的回归方程类型?(给出判断即可,不必说明理
由)并由判断结果及表中数据,求出 关于 的回归方程;
附:回归方程 中, ;
参考数据
81.
5215 2347.3 33.6 27 3.6
3
(2)现在有10根棉花纤维,其中有6根为长纤维,4根为短纤维,从中随机抽取3根棉
花纤维,设抽到的长纤维棉花的根数为X,求X的分布列.
▲
19.(17分)英国数学家泰勒发现了如下公式: ,其中
, 为自然对数的底数, .以上公式称为泰勒公式.设
, ,根据以上信息,并结合高中所学的数学知识,解决如下问
题:
高二数学 第 4 页 共 5 页(1)证明: ;
(2)设 ,证明: ;
(3)设实数 使得 对 恒成立,求 的最大值.
▲
高二数学 第 5 页 共 5 页