文档内容
2024年11月
绵阳南山中学 2024 年秋季高 2023 级半期考试
数学试题
本测评题分试题卷和答题卷两部份,试题卷共4页,满分150分,时间120分钟.
注意事项:
1、答题前,请将本人的信息用 毫米的黑色墨水签字笔或黑色墨水钢笔填在答题卡的对
应位置上;
2、选择题的答案,必须使用 铅笔在答题卡上将所选答案对应的标号涂黑;
3、请用 毫米的黑色墨水签字笔或黑色墨水钢笔将每个题目的答案答在答题卷上每题对
应的位置上,答在试题卷上的无效.作图一律用 铅笔或 毫米黑色签字笔;
第Ⅰ卷(选择题,共58分)
一、单项选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只
有一个是符合题目要求的.
1.直线 的倾斜角是( )
A. B. C. D.
2.在 中, 则顶点 的轨迹方程( )
A. B.
C. D.
3.已知 为 在坐标平面 内的射影,则 ( )
A. B. C.2 D.
4.直线 与圆 的位置关系为( )
A.相离 B.相交 C.相切 D.无法确定
5.与椭圆 共焦点且过 的双曲线方程为( )
A. B.
C. D.
6.在平行六面体 中, 若
则 =( )
A. B.
第 1 页 共 4 页C. D.
7.已知四棱锥 的底面为正方形, 平面 , ,点 是 的
中点,则点 到直线 的距离是( )
A. B. C. D.
8.在平面直角坐标系 中,点 ,若点 满足 ,则
的最大值为( )
A.7 B.9 C.11 D.13
二、多项选择题:本题共3小题,每小题6分,共18分,在每小题给出的四个选项中,有
多项符合题目要求,全部选对得6分,部分选对得部分分,有选错项得0分.
9.下列关于空间向量的命题中,是真命题的有( )
A.将空间所有的单位向量平移到一个起点,则它们的终点构成一个球面
B.若非零向量 ,满足 则有
C.与一个平面法向量共线的非零向量都是该平面的法向量
D.设 为空间的一组基底,且 则 四点共
10.若方程 所表示的曲线为 ,则( )
A.曲线 可能是圆
B.当 时,表示焦点在 轴上的椭圆,焦距为
C.若 ,则 为椭圆
D.若 为椭圆,且焦点在 轴上,则
11.过点 的直线与圆 相切,切点分别为 ,则( )
A.当 时, B.存在 ,使得
C.直线 经过点 D.直线 与直线 的交点在定圆上
三、填空题:本大题共3小题,每小题5分,共15分.请将答案填写在答题卷中的横线
上.
12.双曲线 的左右焦点分别是 , 是双曲线左支上一点,且
第 2 页 共 4 页则 .
13.已知椭圆 的左、右焦点分别为 过 作x轴垂线交椭圆于P,
若 ,则该椭圆的离心率是 .
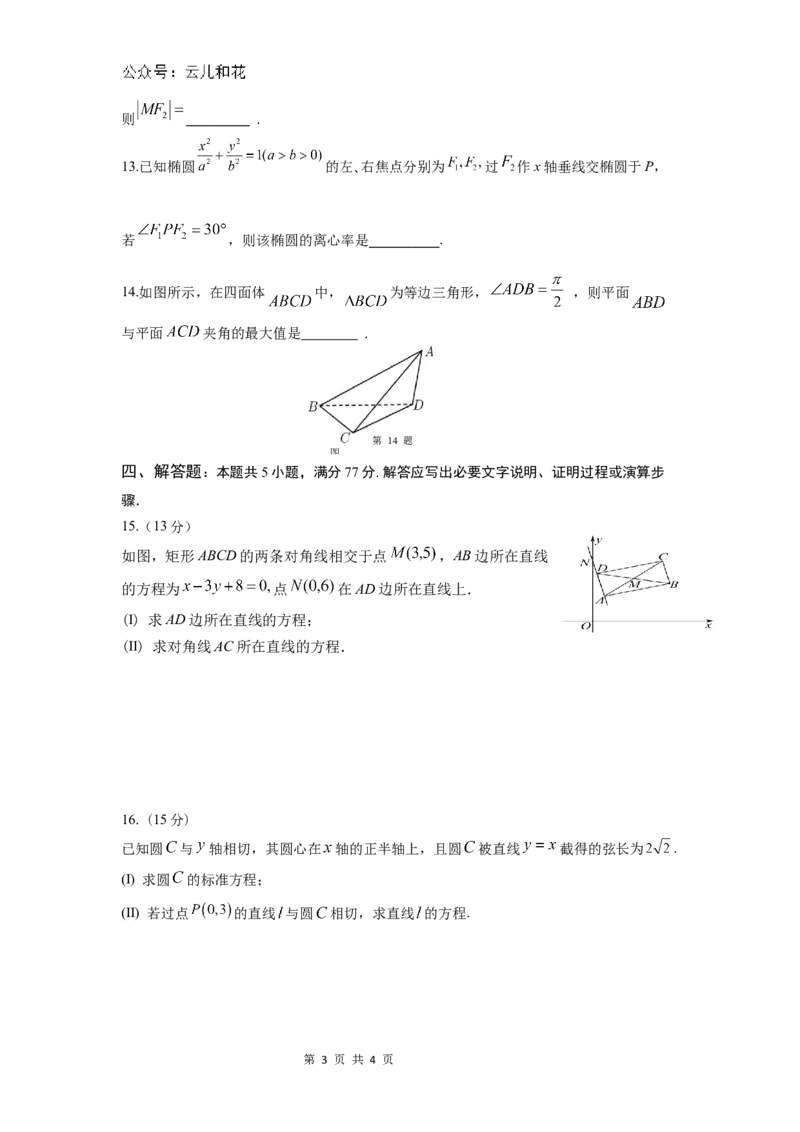
14.如图所示,在四面体 中, 为等边三角形, ,则平面
与平面 夹角的最大值是 .
第 14 题
图
四、解答题:本题共5小题,满分77分.解答应写出必要文字说明、证明过程或演算步
骤.
15.(13分)
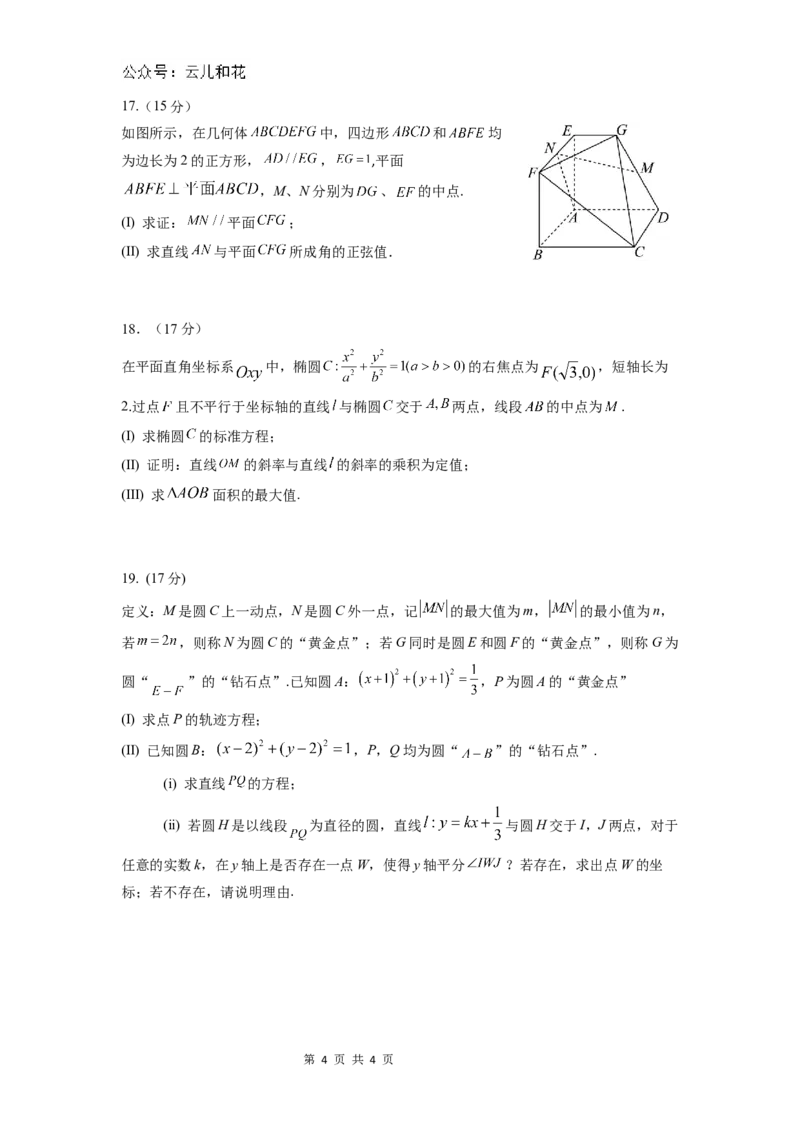
如图,矩形ABCD的两条对角线相交于点 ,AB边所在直线
的方程为 点 在AD边所在直线上.
(Ⅰ) 求AD边所在直线的方程;
(Ⅱ) 求对角线AC所在直线的方程.
16. (15分)
已知圆 与 轴相切,其圆心在 轴的正半轴上,且圆 被直线 截得的弦长为 .
(Ⅰ) 求圆 的标准方程;
(Ⅱ) 若过点 的直线 与圆 相切,求直线 的方程.
第 3 页 共 4 页17.(15分)
如图所示,在几何体 中,四边形 和 均
为边长为2的正方形, , ,平面
,M、N分别为 、 的中点.
(Ⅰ) 求证: 平面 ;
(Ⅱ) 求直线 与平面 所成角的正弦值.
18.(17分)
在平面直角坐标系 中,椭圆 的右焦点为 ,短轴长为
2.过点 且不平行于坐标轴的直线 与椭圆 交于 两点,线段 的中点为 .
(Ⅰ) 求椭圆 的标准方程;
(Ⅱ) 证明:直线 的斜率与直线 的斜率的乘积为定值;
(Ⅲ) 求 面积的最大值.
19. (17分)
定义:M是圆C上一动点,N是圆C外一点,记 的最大值为m, 的最小值为n,
若 ,则称N为圆C的“黄金点”;若G同时是圆E和圆F的“黄金点”,则称G为
圆“ ”的“钻石点”.已知圆A: ,P为圆A的“黄金点”
(Ⅰ) 求点P的轨迹方程;
(Ⅱ) 已知圆B: ,P,Q均为圆“ ”的“钻石点”.
(ⅰ) 求直线 的方程;
(ⅱ) 若圆H是以线段 为直径的圆,直线 与圆H交于I,J两点,对于
任意的实数k,在y轴上是否存在一点W,使得y轴平分 ?若存在,求出点W的坐
标;若不存在,请说明理由.
第 4 页 共 4 页