数学试题_2024-2025高二（7-7月题库）_2024年12月试卷_1222四川省南充市嘉陵一中2024-2025学年高二上学期12月月考_四川省南充市嘉陵一中2024-2025学年高二上学期12月月考数学试题PDF版含答案

秘密★启用前 嘉陵一中高 2023 级高二上期 12 月考 数学试卷 时间：120分钟 总分：150分 注意事项： 1. 答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。 2. 回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。 如需改动，用橡皮擦干净后，再选涂其它答案标号。回答非选择题时，将答案写在答题卡上。 写在本试卷上无效。 3. 考试结束后，将答题卡交回。 一、单项选择题：本题共 8小题，每小题 5分，共 40分．在每个小题绐岀的四 个选项中，只有一项是符合题目要求的． 1. 下列各组向量中不 ． 平 ． 行 ． 的是（ ） r r r r A. a 1,1,2 ，b 2,2,4  B. c 1,0,0 ，d 3,0,0  r r ur r C. e 1,1,0 ， f  0,0,0  D. g 2,3,5 ，h 2,3,5    2. 经过点 1, 3 ，倾斜角为120的直线方程为（ ） A. 3x y2 3 0 B. 3x y 0 C. x 3y40 D. x 3y20  3. 已知A  1,1,1  ，B 3,1,5  ，则 AB 的值为（ ） A.4 B. 4 2 C.5 D. 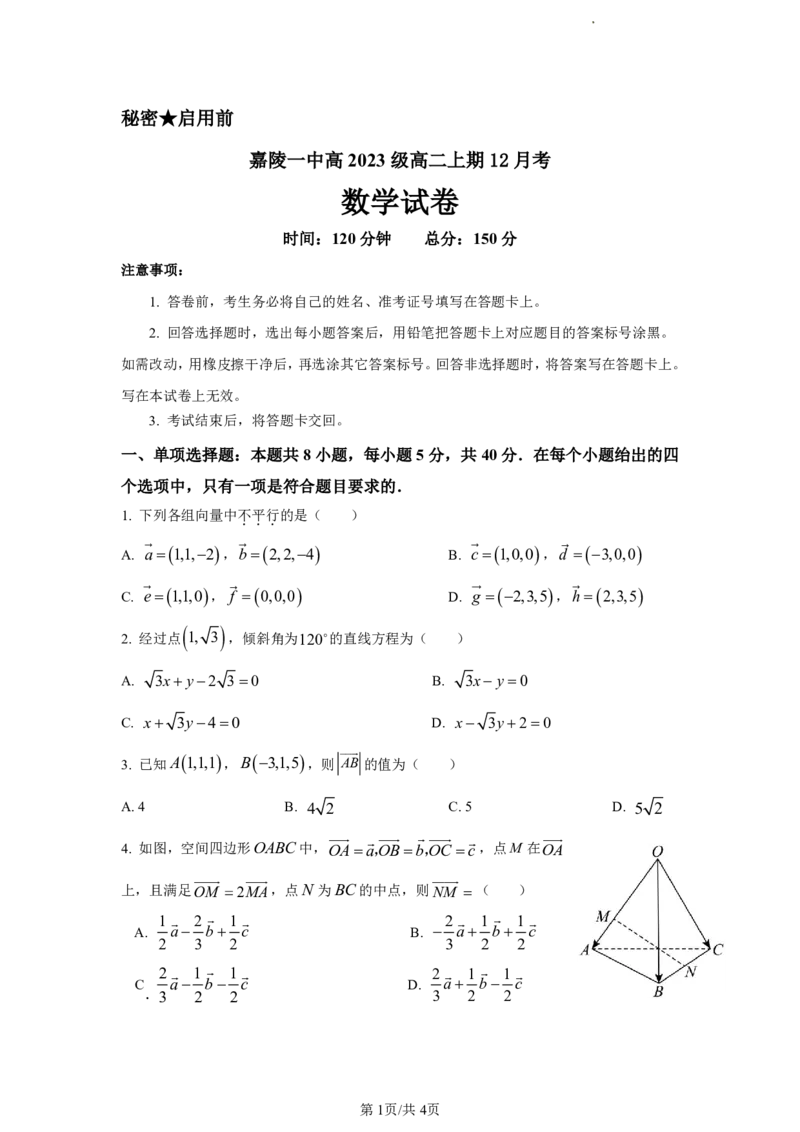5 2        4. 如图，空间四边形OABC中，OAa，OBb，OC c，点M 在OA    上，且满足OM 2MA，点N 为BC的中点，则NM （ ） 1  2  1  2  1  1  A. a b  c B.  a b c 2 3 2 3 2 2 2  1  1  2  1  1  C a b c D. a b  c . 3 2 2 3 2 2 第1页/共4页 学科网（北京）股份有限公司5. 抛掷一枚质地均匀的骰子两次，A表示事件“第一次抛掷，骰子正面向上的点数是3”，B 表示事件“两次抛掷，骰子正面向上的点数之和是4”，C表示事件“两次抛掷，骰子正面向上 的点数之和是7”，则（ ） A.A与B互斥 B.B与C互为对立 C.A与B相互独立 D.A与C相互独立 x2 y2 6. 已知双曲线  1(a0,b0)的左､右焦点分别为F,F ,P为双曲线上第二象限内 a2 b2 1 2 b 一点，若渐近线 y  x垂直平分线段PF ， PF 2a，则双曲线的离心率为（ ） 2 1 a 5 A. 5 B. 3 C. 2 D. 2 x2 y2 7. 已知双曲线C:  l  a 0 ，过左焦点F 的直线l与双曲线交于A,B两点.若存在 a2 4 4条直线l满足 AB 8，则实数a的取值范围是（ ） A.  1,16  B.  1,8  C.  1,4  D.  1,2  8．在棱长为1的正方体ABCDABCD 中，M 是棱AA的中点， 1 1 1 1 1 点P在侧面ABBA 内，若DPCM ，则PBC的面积的最小值是 1 1 1 ( ) 2 5 5 5 A． B． C． D． 5 5 10 5 二、多项选择题：本题共 4 小题，每小题 5 分，共 20 分．(在每小题给出的选项 中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分) 9. 关于空间向量，以下说法正确的是（ ） A. 空间中的三个向量，若有两个向量共线，则这三个向量一定共面  1 1 1 B. 若对空间中任意一点O，有OP OA OB OC，则P,A,B,C四点共面 6 3 2        C. 已知向量{a,b,c}组是空间的一个基底，则{a,b,ca}也是空间的一个基底     D. 若ab 0，则a,b 是钝角 第2页/共4页 学科网（北京）股份有限公司10. 下列说法错 ． 误 ． 的是（ ） A. 直线l:mx y2m0恒过定点(1,2) B. 经过点P(2,1)，且在x，y轴上截距互为相反数的直线方程为x y10 C. 直线l过点P(1,0)，且与以A(2,1),B(0, 3)为端点的线段有公共点，则直线l的斜率k的 取值范围是 3 k 1 D. 已知直线l 过点A(3,a),B(a2,3)，直线l 过点C(2,3),D(1,a2)，若l l ，则 1 2 1 2 a 0． x2 y2 11. 已知双曲线C :x2 y2 1与椭圆C :  1  b0 的一个交点为M ，A,B分 1 2 b2 1 b2 别是C 的左、右顶点，S,T 分别是C 的左、右顶点，则（ ） 1 2 7 A. 直线MA与直线MB的斜率之积为1 B. 若b2 3，则tanAMB 24 2 5 C. 若 MS  MT 2，则b2 1 D. 若△MAB的面积为 ，则b2 2 5 .三、填空题：本题共 3小题，每小题 5分，共计 15分．  12. 已知a  1,1,1  为平面的一个法向量，A  1,0,0  为内的一点，则点D  1,1,2  到平 面的距离为_________． 13. 当原点O到动直线l:xmy2m10  mR  的距离最大时，实数m的值为 __________. 14.已知双曲线C: - =1(a>0，b>0)的离心率为 ，其左、右焦点分别为F ，F ，过F 作C 1 2 2 2 2 10 2 2 3 的一条渐近线的垂线并交C于M，N两点，若|MN|= ，则△MNF 1 3 的周长为 . 4 四、解答题（本大题共 5小题，共77分．解答应写出文 字说明，证明过程或演算步骤）     15．（13分）已知直线l经过点P 1,0 ，直线l截圆C的最长弦长为2，圆心为C 2,3 . （1）求圆C的标准方程；（2）若直线l与圆C相切，求直线l的方程. 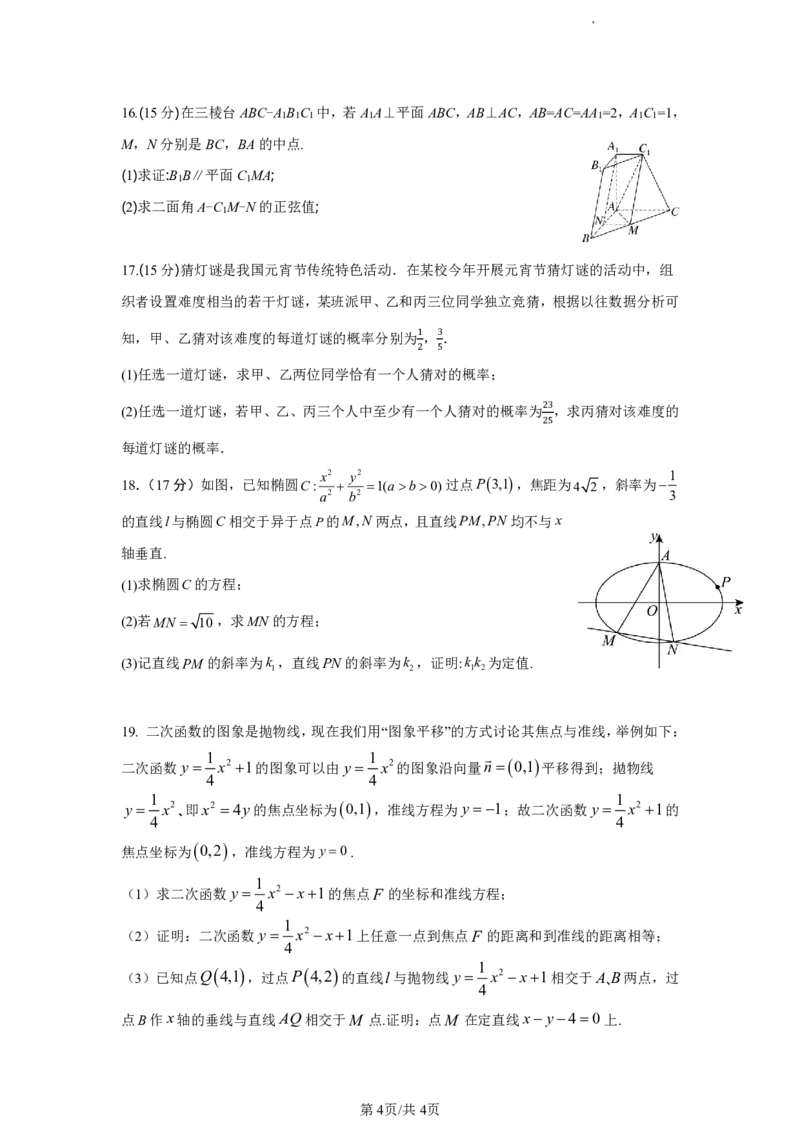第3页/共4页 学科网（北京）股份有限公司16.(15分)在三棱台ABC-A B C 中，若A A⊥平面ABC，AB⊥AC，AB=AC=AA =2，A C =1， 1 1 1 1 1 1 1 M，N分别是BC，BA的中点. (1)求证:B B∥平面C MA; 1 1 (2)求二面角A-C M-N的正弦值; 1 17.(15分)猜灯谜是我国元宵节传统特色活动．在某校今年开展元宵节猜灯谜的活动中，组 织者设置难度相当的若干灯谜，某班派甲、乙和丙三位同学独立竞猜，根据以往数据分析可 知，甲、乙猜对该难度的每道灯谜的概率分别为 ， ． 1 3 (1)任选一道灯谜，求甲、乙两位同学恰有一个人2猜对5 的概率； (2)任选一道灯谜，若甲、乙、丙三个人中至少有一个人猜对的概率为 ，求丙猜对该难度的 23 每道灯谜的概率． 25 18．（17分）如图，已知椭圆C: x2  y2 1(ab0)过点P3,1，焦距为4 2，斜率为 1 a2 b2 3 的直线l与椭圆C相交于异于点P的M,N两点，且直线PM,PN 均不与x 轴垂直. (1)求椭圆C的方程； (2)若MN  10，求MN的方程； (3)记直线PM 的斜率为k ，直线PN的斜率为k ，证明:kk 为定值. 1 2 1 2 19. 二次函数的图象是抛物线，现在我们用“图象平移”的方式讨论其焦点与准线，举例如下： 1 1  二次函数 y  x2 1的图象可以由 y  x2的图象沿向量n  0,1  平移得到；拋物线 4 4 1 1 y  x2､即x2 4y的焦点坐标为0,1，准线方程为y 1；故二次函数y  x2 1的 4 4 焦点坐标为  0,2  ，准线方程为y0. 1 （1）求二次函数y  x2 x1的焦点F 的坐标和准线方程； 4 1 （2）证明：二次函数y  x2 x1上任意一点到焦点F 的距离和到准线的距离相等； 4 1 （3）已知点Q  4,1  ，过点P  4,2  的直线l与抛物线 y  x2 x1相交于A､B两点，过 4 点B作x轴的垂线与直线AQ相交于M 点.证明：点M 在定直线x y40上. 第4页/共4页 学科网（北京）股份有限公司