文档内容
2024 级高二年级第一学期阶段考试 数学科试卷
注意事项:
1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡指定位置.
2.选择题的作答:每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂
黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效.
3.非选择题的作答:用黑色签字笔直接答在答题卡上对应的答题区域内.
4.考试结束后,请将答题卡上交.
一.单选题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有
一项是符合题目要求的.
1.集合 , ,则 ( )
2
A. ={ | <1}B. ={ | −2 <0}C. ∩ = D.
2.若 { |0< <1} { |−1<在 <0} 上是{ 单|−调1函<数 ,<则2}的取值{ 范|0围<是 (<2})
2
A. =−2 B −.2 +1 + C 3. −1,2 D.
3 9 3 9 9 3
3.已知复2,+ 数 ∞ 满足 −2,2 ,则 − 的 ∞ 虚 ,− 部2为( ) −∞,−2 ∪ 2,+∞
A.1 2 +B .=3−i C. D.
4.已知 且 −1 ,则 的最大i 值为( ) −i
A.2 >0, >0 B 2. + 5 5 =10 C. D.
3 5
5.若 ,则 ( ) 2 2
2
A.tan =6 cos B .+sin2 = C. D.
13 13 1 1
6.已知37 为空间内三 − 个3不7 共面的向量,平面4和平面 的法向量分别 − 为4
和 ��1�, ��2�, ��3� ,若 ,则 ( ) � �= ��1�+ ��2�+
3 ��3�A.� �5=− ��1�+2 ��2�+ B �.�3� ∥ + C=.3
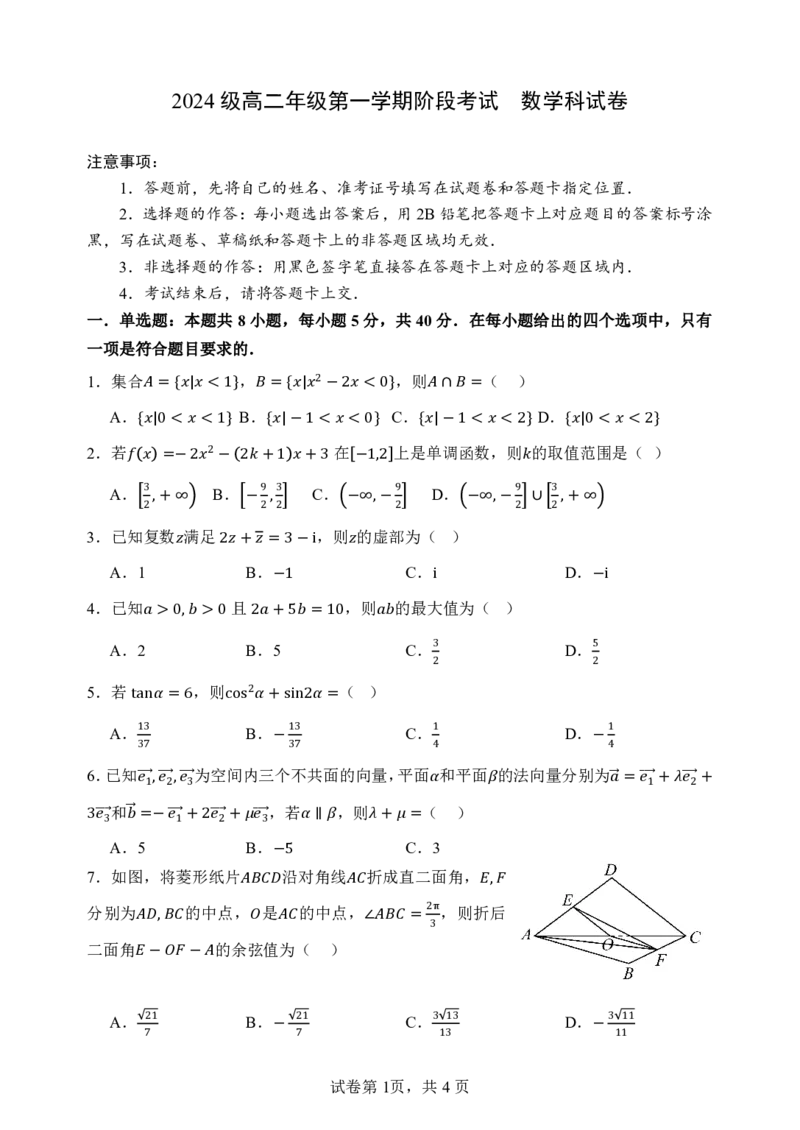
7.如图,将菱形纸片
−
沿
5
对角线 折成直二面角,
分别为 的中点, 是 的中点 , ,则折 后,
2π
二面角 , 的余弦 值 为 ( ) ∠ = 3
− −
A. B. C. D.
21 21 3 13 3 11
7 − 7 13 − 11
试卷第1页,共4页8.19世纪美国天文学家西蒙·纽康和物理学家本·福特提出本·福特定律——在大量10进制
随机数据中,以数 开头的数出现的概率 满足 ,如斐波那契
∗ 10
数、阶乘数、素数等 都 比 ∈ 较 符合该定律.后来常有数 学 爱好者用 1− 此 定 律来 = 检 lg 验 +某1 些经济数据、
选举数据等大数据的真实性.若 ,则 的最大值为( )
log23×log35 ∗
� =1 ≤ 1+log25 ∈
A.6 B.5 C.4 D.3
二.多选题:本题共3小题,每小题6分,共18分,在每小题给出的选项中,有多项符
合题目要求,全部选对得6分,有选错得0分,部分选对得部分分.
9.下列命题中正确的是( )
A.若 是空间任意四点,则有
B.若直 线, ,的 ,方 向向量与平面 的法向量 ��� 的��+夹 �角�� ��为+ ��� ��+, �直�� ��线=与�0�平面 所成的角等于
C.已知 是空间的一个 基底,则 130° 也是空 间的一个基底 50°
D.已知 �为 �,� 坐�,� �标原点,向量 � �+� �,,� �+� �,� �+� �+� � , ,
则点 不能构成三角形 ��� ��=−� +2� −� � ��� ��=−3� +6� −3� � ��� ��=−2� +4� −2� �
10.若函 数, , 的图象与函数 的图象交点的横坐标所在的区间为
1
, 则 的 = 可 2 能 e 取值为( ) = +5
, A+.1 B. C.1 D.2
11.已知
−
正
2
方体
−1
棱长为1,P是 上的一个动点,下列结论正确的是( )
A.当点P 在 直 线 − 1 上1 运1 动1时,一定有 1
B.当点P在直线 1 上运动时,三棱锥 1 ⊥ 的1 体积不变
1 1−
C. 的最小值为
+ 2− 2
D.以点B为球心, 为半径的球面与平面 的交线长为
2 6
三.填空题:本题共3小2题,每小题5分,共1 5 分1 . 3 π
12.某地区采用分层抽样的方法,抽取一定数量的高中学生参加禁毒知识竞赛.若得到的
样本中高二的学生数量比高一多40人、比高三少20人,且该地区高一、高三学生数之比
为 ,则样本容量为 .
13.2:过3 、 两点的直线的倾斜角为 ,那么实数 .
−1, +1,4 45° =
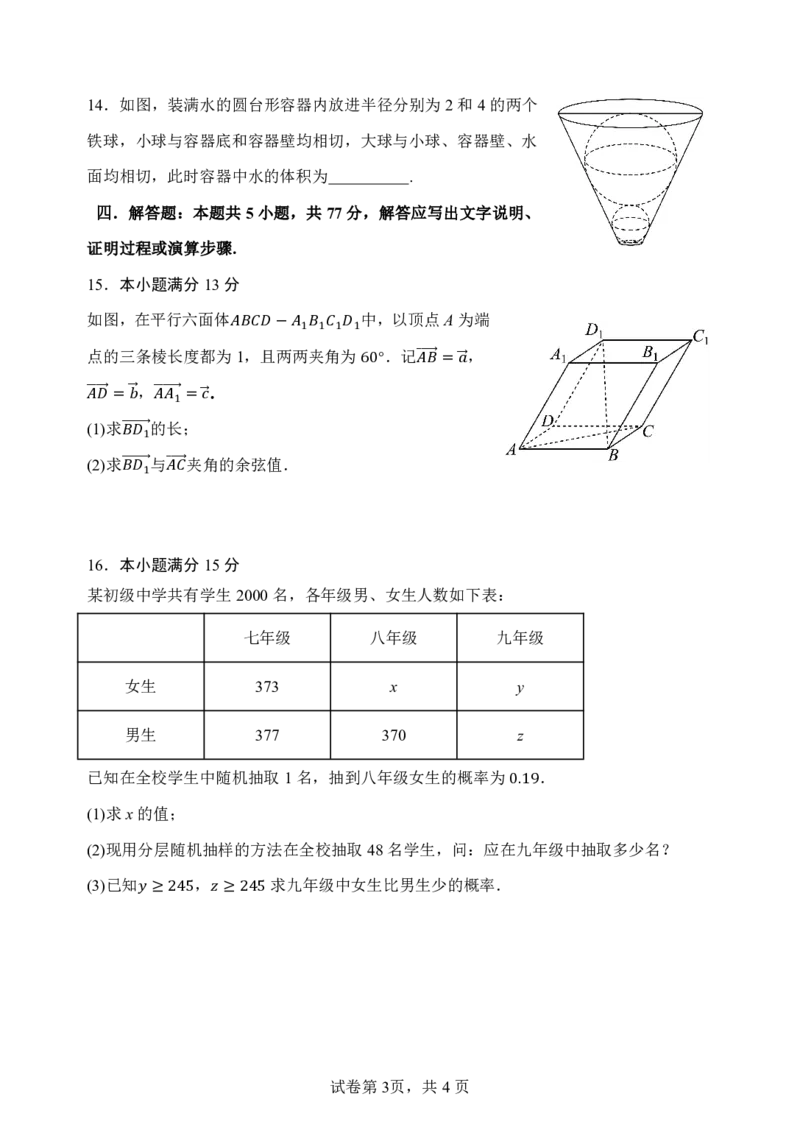
试卷第2页,共4页14.如图,装满水的圆台形容器内放进半径分别为2和4的两个
铁球,小球与容器底和容器壁均相切,大球与小球、容器壁、水
面均相切,此时容器中水的体积为 .
四.解答题:本题共5小题,共77分,解答应写出文字说明、
证明过程或演算步骤.
15.本小题满分13分
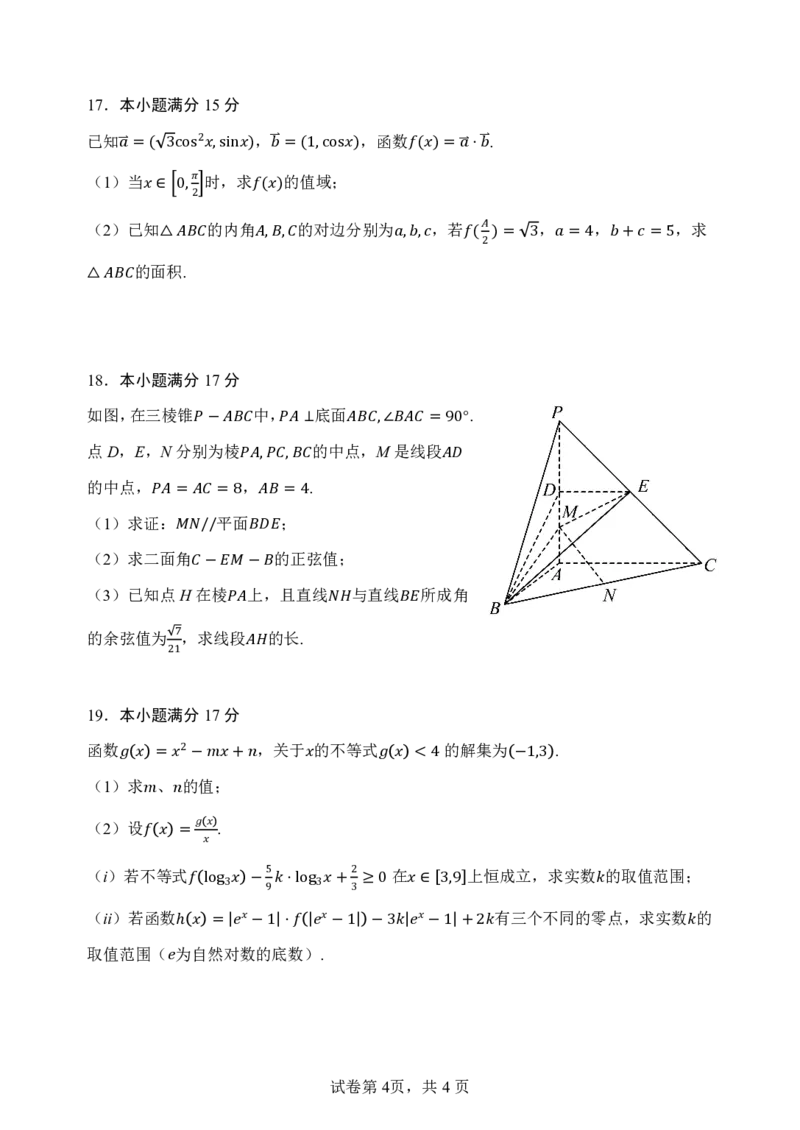
如图,在平行六面体 中,以顶点A为端
点的三条棱长度都为 1 , 且 −两 两1夹 1角 1为 1 .记 ,
, . 60° ��� ��=� �
�(�1� �)�求=� � 的 ��� 长��1�;=� �
(2)求 ��� ��1�与 夹角的余弦值.
��� ��1� ��� �
16.本小题满分15分
某初级中学共有学生2000名,各年级男、女生人数如下表:
七年级 八年级 九年级
女生 373 x y
男生 377 370 z
已知在全校学生中随机抽取1名,抽到八年级女生的概率为 .
(1)求x的值; 0.19
(2)现用分层随机抽样的方法在全校抽取48名学生,问:应在九年级中抽取多少名?
(3)已知 , 求九年级中女生比男生少的概率.
≥245 ≥245
试卷第3页,共4页17.本小题满分15分
已知 , ,函数 .
2
(1)� �当=( 3cos 时 ,s,in求 ) � � 的=值(1域,co;s ) ( )=� �⋅� �
∈ 0,2 ( )
(2)已知 的内角 的对边分别为 ,若 , , ,求
的面
△
积
.
, , , , (2)= 3 =4 + =5
△
18.本小题满分17分
如图,在三棱锥 中, 底面 .
点D,E,N分别 −为 棱 ⊥的中点 , M,∠ 是 线 段=90°
的中点, , , , .
(1)求证 : = =平面8 ;=4
(2)求二面角 // 的正弦值;
(3)已知点H 在−棱 上−, 且直线 与直线 所成角
的余弦值为 ,求线段 的长.
7
21
19.本小题满分17分
函数 ,关于 的不等式 的解集为 .
2
(1) 求 =、 的−值 ; + <4 −1,3
(2)设 .
=
(i)若不等式 在 上恒成立,求实数 的取值范围;
5 2
(ii)若函数
log3 −9 ⋅log3 +3≥0 ∈ 3,9
有三个不同的零
点,求实数 的
取值范围( 为ℎ 自 然=对 数−的1底⋅数 ) . −1 −3 −1 +2
试卷第4页,共4页2024级高二年级第一学期数学阶段考试参考答案
一.选择题
题号 1 2 3 4 5 6 7 8 9 10 11
答案 A D B D A B A C ACD BC ABD
二.填空题
12.460; 13.1; 14.
15.(1)由题意知: , 72π ,
∴ � � = � � = � � =1 <,� �,� �>=<� �,� �>=<� �,� �>=60°
1
� �⋅� �=� �⋅� �=� �⋅� �=1×1×cos60°=2
又∵ ,
��� ��1�= ��� ��+ ��� ��1�+ ���1� ���1�=−� �+� �+� �
∴ ,
2 2
2 2 2
∴ ��� ��1� = � �+,� �即−� � 的=长 � � 为+� �,+� � +2� �⋅� �−2� �⋅� �−2� �⋅� �=1+1+1−1=2
(2 �)�� ��∵1� = 2 ��� ��1� 2,
��� �= ��� ��+ ��� ��=� �+� �
∴ ,∴ ,
2 2 2 2 1
��� � = � �+� � =� � +2� �⋅� �+� � =1+2×2+1=3 ��� � = 3 ,
2 2
� ∴ �� ��1�⋅ ��� �= � �+� �−� � ⋅ � �+� � =� �⋅� �+,� �⋅即� �−� �与+� � 夹+角 � � 的⋅� �余−弦� �值⋅� � 为=1.
��� ���1�⋅ ��� �� 1 6 6
cos< ��� ��1�, ��� �>= ��� ���1� ��� �� = 2× 3= 6 ��� ��1� ��� � 6
16.【详解】(1)由题意 , .
(2)九年级人数为 2000 =0.19 ∴ =380 ,
+ =2000−(373+377+380+370)=500
现用分层随机抽样的方法在全校抽取48名学生,应在九年级抽取的人数为
500
(名).
2000×48= 12
(3)设九年级女生比男生少为事件 ,九年级女生数,男生数记为 ,
由(2)知 , , . ( , )
满足题意的 所+有 样=本50点0 是 ∈
(245,255),(246,254),(247,253),(248,25,2共),(12149个,2,51),
(其25中0事,25件0),包(2含51的,24样9本),(点25是2,248),(253,247),(254,246),(255,245) 共5个,
(245,255),(246,254),(247,253),(248,252),(249,251),
.
5
∴ ( )= 11
试卷第5页,共4页17.【详解】(1)∵ , ,函数 .
2
∴ � �=( 3cos ,sin ) � �=(1,cos ) ( )=� �⋅� �
2
= 3cos +sin cos
3 1 π 3
= 2 1+cos2 +2sin2 =sin 2 +3 + 2
又 , 得 , ,
π π π 4 3 π
0≤ ≤ 2 3 ≤2 +3 ≤3π − 2 ≤sin 2 +3 ≤1
.
π 3 3
0≤sin 2 +3 + 2 ≤ 2 +1
即函数 在 上的值域为 .
π 3
= ∈ 0,2 0, 2 +1
(2) ,
π 3
∵ 2 = 3 ∴ sin +3 = 2
由 ,知 ,
π π 4
∈ 0,π 3 < +3 <3π
解得: ,所以 ,
π 2 π
由余弦定 + 理3知 = :3π = 3 ,即 ,
2 2 2 2 2
= ,因+ 为−2 cos ,所以16= ,+ −
2
∴∴16= + −3
.
+ =5 =3
1 3
18. 【 △ 详 解 = 】(2 Ⅰ ) sin 如 图 = 所4示 3 建立空间直角坐标系.
证(明0,0:,0), (4,0,0), (0,8,0), (0,0,4),. 设(0,4,4), (0,0为,2)平, 面(2,4,0),
的法 ��� �� 向=量(,0,则4,0), ��� ��=(4,0,,即−4) � �=( , .不, )妨设
� �⋅ ��� ��=0 4 =0
=
,可得 ,又 ,
� �⋅ ��� ��=0 4 −4 =0
1可得 � �=(1,0.因,1)为 ���平 ���面=(2,4,,−2所)以 平
面 ��� ���,⋅� �=0 ⊄ //
( Ⅱ) 解:易知 为平面 的一个法向量.
设 为 ��� 1 �平 = 面 (1,0,0) 的法向量 , 则 ,
��� 2 �⋅ ��� ��=0
��� 2 �=( , , )
因为 , , ��� 2 �所⋅ �以�� ��=0 .
−4 −2 =0
��� ��=(0,−4,−2) ��� ��=(4,0,−2)
4 −2 =0
试卷第6页,共4页不妨设 ,可得 ,因此有 ,
� �1⋅� �2 6
=2 ��� 2 �=(1,−1,2) cos ��� 1 �, ��� 2 � = � �1 � �2 = 6
于是 .所以,二面角 的正弦值为 ;
30 30
(Ⅲ)sin依� 题�1,意� �2 ,=设 6 −, − 6
则 ,进而可 得=ℎ(0 ≤ℎ≤ 8) ,
由已 (知0,0,,ℎ得) ��� ��=(−2,−4,ℎ) ��� ��=(−,4,4,4)
⋅ 4ℎ−8 7
cos〈 ��� ��, ��� ��〉 = = ℎ 2 +20×4 3= 21
整理得 , 解得 ,或 .
2 16
5ℎ −21ℎ+16=0 ℎ= 5 ℎ=1
所以,线段 的长为 或1
16
19.【详解】( Ⅰ)因为 5 的解集为 ,
2
即方程 <的4两⇒根 为−-1 和 +3, −4<0 −1,3
2
− + −4=0
由韦达定理可知 ,解得 .
−1 +3= =2
(Ⅱ)(i)由(Ⅰ)可−1得×:3= −4 =1,
1
= = + −2
所以不等式 在 上恒成立,
5 2
log3 −9 ⋅log3 +3≥0 ∈ 3,9
等价于 在 上恒成立,
5 1 4
2
9 ≤ log3 −3log3 +1 ∈ 3,9
令 ,因为 ,所以 ,
1 1
=log3 ∈ 3,9 ∈ 2,1
则有 在 恒成立,
5 2 4 1
9 ≤ −3 +1 ∈ 2,1
令 , ,则 ,
2 4 2 2 5 1 2 5
= −3 +1= −3 +9 ∈ 2,1 min = 3 =9
所以 ,即 ,所以实数 的取值范围为 .
5 5
(ii)9因 ≤ 为9 ≤ 1 −∞,1 ,
2
令 ℎ ,=由 题意−可1 知− 3 +2 ⋅ ,−1 +2 +1
令 = −1 ∈ 0,,+∞ ,
2
则函 数 = − 3 +2 +2 +1 ∈ 0,+∞ 有三个不同的零点,
2
等价于ℎ = −1 − 3 +2 ⋅ −在1 +2 +1 有两个零点,
2
= − 3 +2 +2 +1 ∈ 0,+∞
试卷第7页,共4页当 时,方程 ,此时 ,解得 或 ,关于
1 2 1 1
的方
=
程
0
有三个零点
,
符合
=
题
0 ⇒
意;
=−2 = −2 =0 =2
当 时,记两个零点为 , ,且 , , ,
≠0 1 2 1 < 2 0< 1 <1 2 ≥1
所以 ,
0 =2 +1> 0
1 =− ≤ 0
2
综上实 数=9的 取+值4范 围>是0 .
1
0,+∞ ∪ −2
试卷第8页,共4页