宁夏吴忠市高三上学期学业水平适应性考试数学答案_2024-2025高三（6-6月题库）_2024年11月试卷_1128宁夏吴忠市高三上学期学业水平适应性考试（全科）

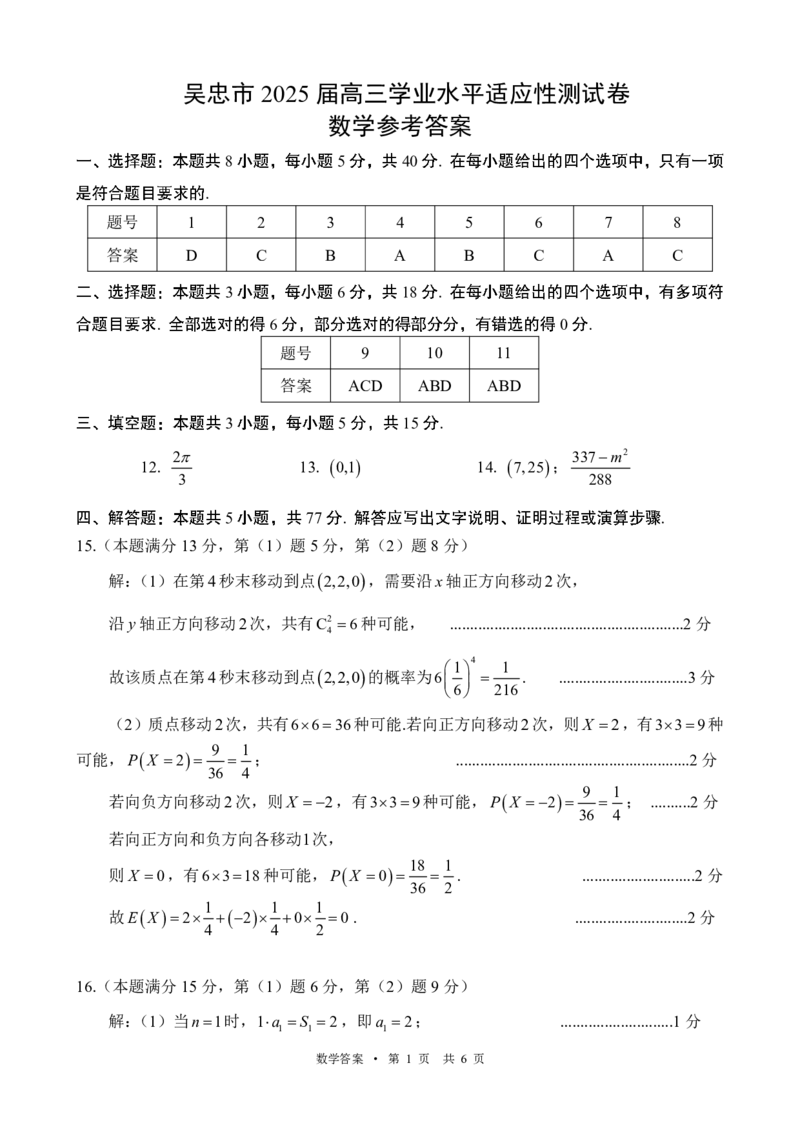
吴忠市 2025 届高三学业水平适应性测试卷
数学参考答案
8 5 40 .
.
题号 1 2 3 4 5 6 7 8
答案 D C B A B C A C
3 6 18 .
. 6 0 .
题号 9 10 11
答案 ACD ABD ABD
3 5 15 .
2 337m2
12. 13.

0,1

14.

7,25
；
3 288
5 77 . .
15.（本题满分13分，第（1）题5分，第（2）题8分）
解：（1）在第4秒末移动到点
2,2,0
，需要沿x轴正方向移动2次，
沿 y轴正方向移动2次，共有C2 6种可能， ..........................................................2分
4
4
1 1
故该质点在第4秒末移动到点 2,2,0 的概率为6   . ................................3分
6 216
（2）质点移动2次，共有6636种可能.若向正方向移动2次，则X 2，有339种
9 1
可能，P  X 2   ； ..........................................................2分
36 4
9 1
若向负方向移动2次，则X 2，有339种可能，P  X 2   ； ..........2分
36 4
若向正方向和负方向各移动1次，
18 1
则X 0，有6318种可能，P  X 0   . ............................2 分
36 2
1 1 1
故E  X 2 2  0 0 . ............................2分
4 4 2
16.（本题满分15分，第（1）题6分，第（2）题9分）
解：（1）当n1时，1a S 2，即a 2； ............................1分
1 1 1
数学答案 · 第 1 页 共 6 页
{#{QQABCYAEogCgABAAAQgCQQmSCkAQkhECAYgOwAAAsAAACBFABCA=}#}当n2时，
有na S S  n1 2n12  n2 2n2n2n ，
n n n1  
得a 2n， ...........................3分
n
若n1，则a 2； ............................1分
1
综上，有a 2n. ............................1分
n
1 1 1 1
（2）b     . ............................2分
n 2n  2n2 2n 4n
1 1 1  1 1 1 
T           
n 2 22 2n 4 42 4n
 n  n
1 1 1 1
1    1   
2 2  4 4  4 1 1 1
     ， ............................2分
1 1 3 2n 3 4n
1 1
2 4
3
显然，T  ，有 T 0， ............................1分
1 4 1
17 4
当n2时，T T  ,且T  ，有 T 1（n2）， ................2分
n 2 16 n 3 n
n

T

i 011 n1
故 i1   1. .........................2分
n n n
17.（本题满分15分，第（1）题5分，第（2）题10分）
解：（1）如图，取PA的中点F ，连接EF ， ............................1分
1
BF，有EF ∥AD，EF  AD，
2
1
又BC∥AD，BC  AD，
2
所以EF∥BC，EF  BC ，
所以四边形BCEF是平行四边形，
所以CE∥BF ， ............................2分
因为CE 平面PAB，BF ⊆平面PAB，
所以CE⊈ ∥平面PAB. ............................2分
数学答案 · 第 2 页 共 6 页
{#{QQABCYAEogCgABAAAQgCQQmSCkAQkhECAYgOwAAAsAAACBFABCA=}#}（2）如图，取AD的中点O，连接OP，OB，
因为PA PD，APD 90，
1
所以AD  PO，PO  AD 1，
2
由BC∥OD，BC OD CD 1，CD OD，
知四边形BCDO是正方形，有AD  BO，OB 1，
因为POBO O，所以AD平面PBO，
因为AD⊆平面ABCD，所以平面ABCD 平面PBO，
在平面PBO内作直线BO的垂线Oz，
则Oz 平面ABCD，有Oz OB，Oz OD，
分别以OB，OD，Oz所在直线为x轴、y轴、z轴，
建立空间直角坐标系， ............................3分
因为BC∥AD，所以BC 平面PBO，
因为BP⊆平面PBO，所以BC  BP，
由PC 2，BC 1，知BP  3，
OP2 OB2 BP2 113 1 2
由cosBOP   ，知BOP ，
2OPOB 211 2 3
 1 3
从而有P ,0, ， ...........................2分
 
 2 2 
A  0,1,0 ，B  1,0,0 ，C  1,1,0 ，
 1 3  
有PA ,1, ，AB  1,1,0 ，BC  0,1,0 ，
 
2 2 
  1 3
  mPA0,  x y z  0,
设平面PAB的法向量为m x,y,z ，由   有2 2 取x1，
mAB 0, 
x y 0,

 
则 y1，z  3，得平面PAB的一个法向量为m 1,1, 3 ， ......3分
 
BCm
5
设直线BC与平面PAB所成的角为，则sin    ......2分
BC m 5
数学答案 · 第 3 页 共 6 页
{#{QQABCYAEogCgABAAAQgCQQmSCkAQkhECAYgOwAAAsAAACBFABCA=}#}18.（本题满分17分，第（1）题3分，第（2）题（ⅰ）8分，（ⅱ）6分）
c 3
解：（1）由题意，有  ， ..........................1分
a 3
2b4， ..............................1分
a2 b2 c2，解得a2 6，b2 4，
x2 y2
故椭圆C的方程为  1. ...........................1分
6 4
x2 y2
（2）l：ykx1（k 0），与  1联立，
6 4
得 23k2  x2 6kx90， ...........................1分
其中 6k 24  23k2  9 72  2k21  0 ， ...........................1分
6k
设P  x ,y ，Q  x ,y ，有x x  ， ...........................1分
1 1 2 2 1 2 23k2
9
x x  . ...........................1分
1 2 23k2
 1   
（ⅰ）由F  ,0 ，E(0,1)，QE FP，
 k 
 1 1
有0x  x     ，即x x  ， ...........................1分
2 1  k  1 2 k
6k 1
有  ， ...........................1分
23k2 k
6
解得k  . ...........................2分
3
（ⅱ）A  0,2 ，B  0,2 ，假设存在直线AP平行于直线BQ，
y 2 y 2
有k k ，有 1  2 ，又y kx 1，y kx 1，
AP BQ x x 1 1 2 2
1 2
kx 1 kx 3
有 1  2 ，得 kx 1  x  kx 3  x ，
x x 1 2 2 1
1 2
有x 3x ， ...........................2分
2 1
6k 3k
代入x x  ，得x  ， ...........................1分
1 2 23k2 1 23k2
数学答案 · 第 4 页 共 6 页
{#{QQABCYAEogCgABAAAQgCQQmSCkAQkhECAYgOwAAAsAAACBFABCA=}#}9k
有x  ， ...........................1分
2 23k2
9 3k 9k 9
代入x x  ，有   ， ...........................1分
1 2 23k2 23k2 23k2 23k2
3k2
整理，得 1，有20，显然矛盾，故不存在 ................1分
23k2
实数k，使直线AP平行于直线BQ.
19.（本题满分17分，第（1）题4分，第（2）题（ⅰ）5分，（ⅱ）8分）
1 2  3 2
解：（1）由题意，有       1，得a 2， .................1分
a  2 
x2 x2
有  y2 1，有y  1 ， .................1分
4 4
1
 2x
x
则 y' 4  ， .................1 分
x2 x2
2 1 4 1
4 4
1  3 3 1
有 y'  ，故该函数在点1, 处的切线方程为y   x1 ，
x1
2 3

 2

 2 2 3
即x2 3y40. .................1分
a b
（2）因为 y是x的“1型函数”，所以  1， .................1分
x y
a b
由 1， 1，有x a， y b. .................1分
x y
a b bx ay bx ay  2
（ⅰ）x y  x y     ab  ab2   a  b ，
 x y y x y x
a b bx ay
当且仅当  1， 
x y y x
即xa ab ，y b ab时“”成立. .................3分
a b bx
（ⅱ）由  1，有y  ， .................1分
x y xa
n
 bx 
记xn  yn  xn 
 
 f(x)（x a）， .................1分
 xa
数学答案 · 第 5 页 共 6 页
{#{QQABCYAEogCgABAAAQgCQQmSCkAQkhECAYgOwAAAsAAACBFABCA=}#} bx  n1b  xa bx nxn1
f '(x)nxn1n    xa n1abn  ......2分
 xa  xa 2  xa n1  
由 f '(x)0，得xan1abn ，
 
当x a,an1abn 时， f '(x)0，f(x)单调递减， ........1分
 
当x an1abn, 时， f '(x)0， f(x)单调递增， ........1分
因此，有
f(x) f(an1abn)  an1abn n    b  an1abn   n   an1abn n  1   n1b  n 
   
an1abn a   n1a 
   
 
n n1
 n  n  n  n n   n n   n n 
 n1an n1bn  n1a  n1b  an1bn1 an1bn1 an1bn1
 
     
....................2分
n1
 n n 
这也就证明了xn  yn an1bn1 （nN）.
 
数学答案 · 第 6 页 共 6 页
{#{QQABCYAEogCgABAAAQgCQQmSCkAQkhECAYgOwAAAsAAACBFABCA=}#}