宁夏吴忠市高三上学期学业水平适应性考试数学_2024-2025高三（6-6月题库）_2024年11月试卷_1128宁夏吴忠市高三上学期学业水平适应性考试（全科）

绝密★启用前
二、选择题：本题共3小题，每小题6分，共18分. 在每小题给出的四个选项中，有多项符合题
吴忠市 2025 届高三学业水平适应性测试卷 目要求. 全部选对的得6分，部分选对的得部分分，有错选的得0分.
数 学
9. 已知z ，z 为方程x2 10x400的根，则（ ）
考试时间：120分钟 满分：150分 1 2
一、选择题：本题共8小题，每小题5分，共40分. 在每小题给出的四个选项中，只有一项是符 A.z z 10
1 2
合题目要求的.
B.z z 10
    1 2
1. 已知集合A x y  x2 ，B x x2 4x30 ，则AB （ ）
C.z  z
1 2
A.  x 2 x3  B.  x x2  C.  x x1,或 x2  D.  x x1 
D. z  z
1 2
2. 已知a0.23，b30.2，clog 3，则（ ）
0.2 1
10. 已知函数 f(x)sin2x ，则（ ）
A.a cb B.a bc C.ba c D.cba sinxcosx
    
3. 已知平面 P nPP 0 ，其中点P  1,2,3 ，法向量n 1,1,1 ，则下列各点中不在平面内 A. f(x)的图象关于原点对称
0 0
的是（ ） B.存在非零常数T ，使得 f(xT) f(x)
A. 1,2,3  B.2,4,5  C.3,4,5  D. 2,4,8 
C. f(x)的最小值为2 2
4. 已知函数 f(x) xa 2 ln(ex 1)是偶函数，则a（ ）
D.方程 f(x)a无解的充要条件是a3,3 
1 1
A. B. C. 0 D. 1 y2
4 2 11. 过双曲线C ：x2  1的右焦点F 作直线l，交双曲线C 于A，B两点，则（ ）
2
5. 过抛物线x2 4y的焦点F 作直线l，交抛物线于A，B两点.若线段AB中点的纵坐标为3，则
AB 等于（ ）
A.双曲线C 的实轴长为2
A. 10 B. 8 C. 6 D. 4 B.当l  x轴时， AB 4
 a
6. 函数 f(x)asinxbcosx图象的一条对称轴为直线x ，则 （ ）
6 b C.当 AB 3时，这样的直线l有3条
3 3
A. 3 B. 3 C. D.
D.当 AB 4时，这样的直线l有4条
3 3
三、填空题：本题共3小题，每小题5分，共15分.
7. 已知A，B，C是球O的球面上的三个点，且ACB 120，AB  3，ACBC 2.若三棱锥
     
6 12. 已知单位向量a，b满足 a2b  3，则a与b的夹角为 .
O ABC的体积是 ，则球O的体积为（ ）
6
13. 不等式x2 ln x  x的解集为 .
A.36 B.24 C.12 D.8
8. 已知cos  1 ，coscos 5 ，则cos2cos2（ ） 14. 已知矩形ABCD，AB 20，BC 15，沿对角线AC将ABC折起（点B在平面ACD外），若
2 12
3 4 7 9 BDm，则m的取值范围是 ，二面角B ACD的余弦值是 （用m表示）.
A. B. C. D.
2 3 6 8
数学试卷 · 第 1 页 · 共 4 页 数学试卷 · 第 2 页 · 共 4 页
{#{QQABCYAEogCgABAAAQgCQQmSCkAQkhECAYgOwAAAsAAACBFABCA=}#}四、解答题：本题共5小题，共77分. 解答应写出文字说明、证明过程或演算步骤.
18.（本题满分17分）
15.（本题满分13分） x2 y2 3
设椭圆C：  1（a b0）的离心率为 ，短轴长为4.
a2 b2 3
在空间直角坐标系Oxyz中，一个质点从原点O出发，每秒向x轴正方向、x轴负方向、y轴
（1）求椭圆C的方程；
正方向、y轴负方向、z轴正方向、或z轴负方向移动1个单位，且向六个方向移动的概率均相等.
（2）过点E(0,1)，且斜率为k的直线l与椭圆C相交于P，Q两点.
（1）求该质点在第4秒末移动到点
2,2,0
的概率；
 
（ⅰ）若直线l与x轴相交于点F ，且QE  FP，求k的值；
（2）设该质点在第2秒末移动到点 x,y,z ，记随机变量X  x yz，求X 的期望E  X .
（ⅱ）已知椭圆C的上、下顶点分别为A，B，是否存在实数k，使直线AP平行于直线BQ？
16.（本题满分15分）
19.（本题满分17分）
已知数列 na 的前n项和S 满足S  n1 2n12（nN*）.
n n n
m m
 x  y
（1）求数列 a 的通项公式； 若变量x，y满足：x 0，y 0，且      1，其中a 0，b0，mZ且m0，
n a b
（2）设b 
1

1
，数列 b 的前n项和为T ， x 表示不超过x的最大整数，
则称y是x的“m型函数”.
n a a 2 n n
n n
 3
（1）已知b1，y是x的“2型函数”，求该函数在点1, 处的切线方程；
 n  T    2  
i
求证： i1 1.
n （2）已知y是x的“1型函数”.
（ⅰ）求x y的最小值；
n1
 n n 
（ⅱ）求证：xn  yn an1bn1 （nN）.
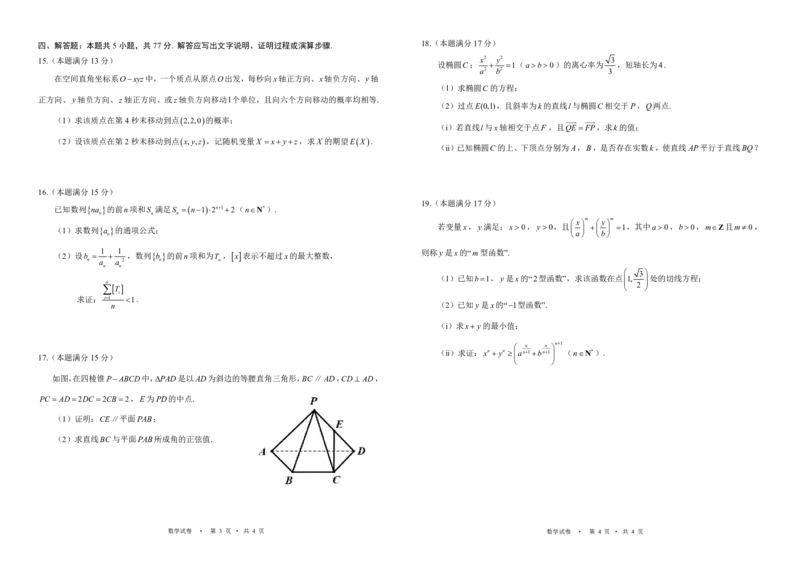
17.（本题满分15分）
 
如图，在四棱锥PABCD中，PAD是以AD为斜边的等腰直角三角形，BC∥AD，CD  AD，
PC  AD 2DC 2CB 2，E为PD的中点.
（1）证明：CE∥平面PAB；
（2）求直线BC与平面PAB所成角的正弦值.
数学试卷 · 第 3 页 · 共 4 页 数学试卷 · 第 4 页 · 共 4 页
{#{QQABCYAEogCgABAAAQgCQQmSCkAQkhECAYgOwAAAsAAACBFABCA=}#}