数学试题答案_2024-2025高二（7-7月题库）_2024年11月试卷_1127重庆市万州二中2024-2025学年高二上学期期中考试_重庆市万州二中2024-2025学年高二上学期期中考试数学试题（PDF版，含答案）

万州二中高 2023 级高二上期中考数学试题答案 一､选择题：本题共 8小题，每小题 5分，共 40分.在每小题给出的四个选项中，只有一项是 符合题目要求的. 【1题答案】A【2题答案】A【3题答案】C【4题答案】A【5题答案】D【6题答案】D【7题答案】A【8 题答案】B 二､多选题：本题共 3小题，每小题 6分，共 18分.在每小题给出的选项中，有多项符合题目 要求.全部选对的得 6分，部分选对的得部分分，有选错的得 0分. 【9题答案】AB【10题答案】BCD【11题答案】ACD 三､填空题：本题共 3小题，每小题 5分，共 15分. 【12题答案】2【13题答案】 31.【14题答案】16 四､解答题：本题共 5小题，共 77分.解答应写出文字说明､证明过程或演算步骤. 【15题答案】解：（1）因为l∥l，所以 22a1a10,   2a5a10, 解得a1……………….6分 a5 a5 （2）令x 0，得y ，即直线l在 y 轴上的截距为 . a1 a1 a5 a5 令y0，得x ，即直线l在x轴上的截距为 . 2a1 2a1 a5 a5 因为直线l在两坐标轴上的截距相等，所以  . a1 2a1 所以a5a20，解得a 5或a 2. 则直线l的方程是9x6y0或3x3y30，即3x2y0或x y10.……….13分 【16题答案】 （Ⅰ）设4x3yt，则直线4x3yt与 C有公共点， t 所以圆心到直线的距离d 4 4，解得20t 20．……….6分 42 32 （Ⅱ）当直线l垂直于x轴时，此时直线方程为x 3，l与圆的两个交点坐标为(3, 7)，(3, 7)，这两 点的距离为2 7 ，满足题意； 1当直线l不垂直于x轴时，设其方程为y4kx3， 即kxy3k40，设圆心到此直线的距离为dd 0，则2 7 2 16d2 ， 3k4 7 得d 3，从而 3，得k  ，此时直线方程为7x24y750， k2 1 24 综上所述，所求直线方程为7x24y750或x 3．………15分 【17题答案】 ……….6分 2……….15分 x2 y2 4 6 【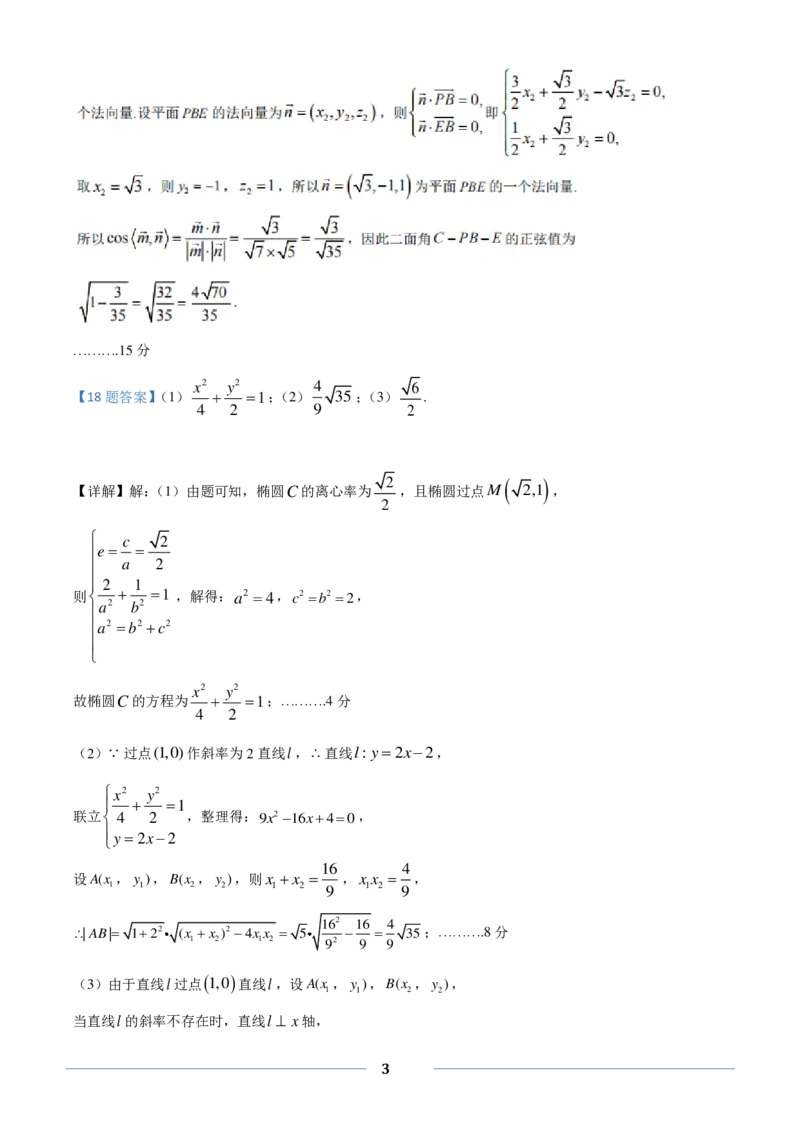18题答案】（1）  1；（2） 35；（3） . 4 2 9 2 2   【详解】解：（1）由题可知，椭圆C的离心率为 ，且椭圆过点M 2,1 ， 2  c 2 e  a 2   2 1 则  1 ，解得：a2 4，c2 b2 2， a2 b2  a2 b2 c2   x2 y2 故椭圆C的方程为  1；……….4分 4 2 （2） 过点(1,0)作斜率为2直线l，直线l:y2x2， x2 y2   1 联立 4 2 ，整理得：9x2 16x40，  y 2x2 16 4 设A(x ，y )，B(x ，y )，则x x  ，x x  ， 1 1 2 2 1 2 9 1 2 9 162 16 4 |AB| 122 (x x )2 4xx  5   35；……….8分 1 2 1 2 92 9 9 （3）由于直线l过点 1,0 直线l，设A(x ，y )，B(x ，y )， 1 1 2 2 当直线l的斜率不存在时，直线l  x轴， 3x2 y2 6 此时将x1代入  1，解得：y  ， 4 2 2  6  6 即A，B的坐标分别为1, ,1, ，     2 2     1 1 6 则OAB的面积为：S  y  y 1  6  ； 2 1 2 2 2 当直线l的斜率存在，且不为0时，可设直线l的方程为：xmy1， x2 y2   1 联立 4 2 ，整理得：  m2 2  y2 2my30，  xmy1 2m 3 则y  y  ,y y  ， 1 2 m2 1 1 2 m2 1 1 1 而OAB的面积为：S  y y 1 y  y 2 4y y ， 2 1 2 2 1 2 1 2 1  2m  2 3 1 4m2 12 即S    4   2 m2 2 m2 2 2  m2 2 2 m2 2 1 16m2 24 1 2 4m2 6 4m2 6     ， 2  m2 2 2 2 m2 2 m2 2 t2 6 令t  4m26  6，则t2 4m2 6，得 m2  ， 4 4m2 6 t 4t 4   S     t  6 所以 m2 2 t2 6 t2 2 2 ， 2 t 4 t 2 2 4 6 由于t  6，由双勾函数的性质得t  6  ， t 6 3 4 4 6  S    t  6 则 2 4 6 2 t t 3 6 所以综上得：S  ， 2 6 所以OAB的面积最大值为 .………17分 2 456