萍乡市2023—2024学年度高三二模数学答案_2024年4月_01按日期_16号_2024届江西省萍乡市高三下学期二模考试_江西省萍乡市2023-2024学年高三下学期二模考试数学试卷

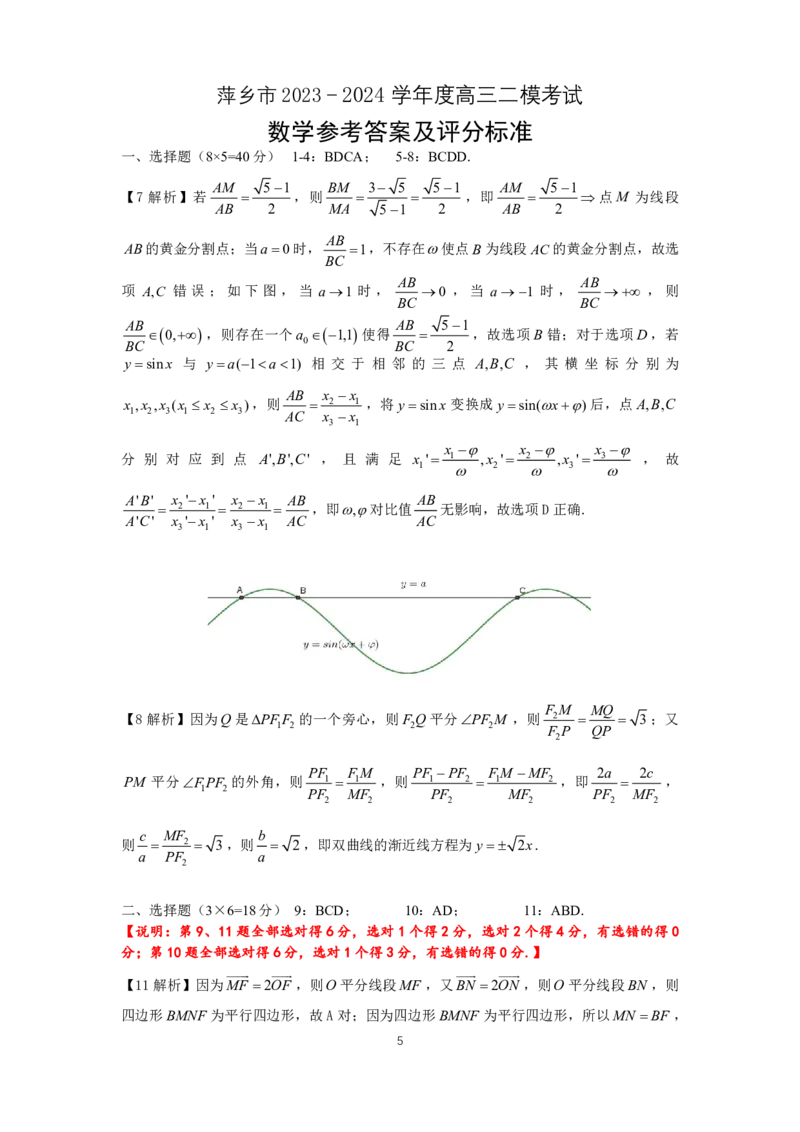
萍乡市 2023－2024 学年度高三二模考试 数学参考答案及评分标准 一、选择题（8×5=40分） 1-4：BDCA； 5-8：BCDD. AM 51 BM 3 5 51 AM 51 【7 解析】若  ，则   ，即  点M 为线段 AB 2 MA 51 2 AB 2 AB AB的黄金分割点；当a0时， 1，不存在使点B为线段AC的黄金分割点，故选 BC AB AB 项 A,C 错误；如下图，当 a1 时， 0 ，当 a1 时，  ，则 BC BC AB AB 51 0,，则存在一个a 1,1使得  ，故选项B 错；对于选项D，若 BC 0 BC 2 ysinx 与 ya(1a1) 相 交 于 相 邻 的 三 点 A,B,C ， 其 横 坐 标 分 别 为 AB x x x ,x ,x (x  x  x )，则  2 1 ，将 ysinx 变换成 ysin(x)后，点 A,B,C 1 2 3 1 2 3 AC x x 3 1 x  x  x  分 别 对 应 到 点 A',B',C' ， 且 满 足 x ' 1 ,x ' 2 ,x ' 3 ， 故 1  2  3  A'B' x 'x ' x x AB AB  2 1  2 1  ，即,对比值 无影响，故选项D正确. A'C' x 'x ' x x AC AC 3 1 3 1 F M MQ 【8解析】因为Q是PFF 的一个旁心，则FQ平分PF M ，则 2   3；又 1 2 2 2 F P QP 2 PF FM PF PF FM MF 2a 2c PM 平分FPF 的外角，则 1  1 ，则 1 2  1 2 ，即  ， 1 2 PF MF PF MF PF MF 2 2 2 2 2 2 c MF b 则  2  3，则  2，即双曲线的渐近线方程为y 2x. a PF a 2 二、选择题（3×6=18分） 9：BCD； 10：AD； 11：ABD. 【说明：第9、11题全部选对得6分，选对1个得2分，选对2个得4分，有选错的得0 分；第10题全部选对得6分，选对1个得3分，有选错的得0分.】     【11解析】因为MF 2OF ，则O平分线段MF ，又BN 2ON ，则O平分线段BN，则 四边形BMNF 为平行四边形，故A对；因为四边形BMNF 为平行四边形，所以MN BF ， 5 {#{QQABBQAAggAIAJAAABhCAQngCkKQkBGCACoGBEAEoAIBSAFABAA=}#}1 1 2 1 1 又   1，故  1，故B对；当AB x轴时，根据对称性，P在y轴 AF BF p AF MN   上，此时OPOF 0，故C错；设A(x,y ),B(x ,y )，因为l 过焦点F，则y y 4，则 1 1 2 2 1 2 y y 4y 4y 4y y 2 16y 4y y2 16y k k  1  2  1  2  1 2 1 2 1 2 0 ， 则 MA MB x 1 x 1 y2 4 y 2 4  y2 4  y2 4  1 2 1 2 1 1 AMOBMO ， 又 NBM BMO ， 则 NFM AMO ，即 PMF 为等腰三角形，且 y 轴为 MF 的垂直平分线，故P必在y轴上.此外，MN  AB， 1 则S S ，则S S  MF  OP  OP ， AMN FMN ANP FMP 2 当MA与抛物线C 相切时， OP 取得最大值1，即S ANP 的最大值为1，故D对. 11 3 15 2 2 4 三、填空题（3×5=15分） 12： ； 13：1； ； 14： , . 72 16  3 3 【说明：第13题全部做对得5分，做对1空得3分.】 四、解答题（共77分） 1 15.（1） f x  x  2lnx1 ，令 f x 0，解得xe  2， ……………………………(2分) 1 当x(0,e  2)时， f x 0， f  x 单调递减； 1 当x(e  2,)时， f(x)0， f  x 单调递增，…………………………………………(4分) 1 1 则 f  x 的单调递减区间为(0,e  2)，单调递增区间为(e  2,)；………………………(6分) （2）依题意，存在x0，使得axlnx，………………………………………………(7分) 令g(x)xlnx，则g(x)lnx1，………………………………………………………(8分) 1 当x(0, )时，g(x)0，g(x)单调递减； e 1 当x( ,)时，g(x)0，g(x)单调递增，…………………………………………(11分) e 1 1 1 故g(x) g( ) ，因此a .……………………………………………………(13分) min e e e 6 16.（1）1 (91644164149)0.8 ；………………………(5分) 15224 （2）X 的值可能为0,1,2,3，………………………………………………………………(7分) 6 {#{QQABBQAAggAIAJAAABhCAQngCkKQkBGCACoGBEAEoAIBSAFABAA=}#}C3 2 C1C2 20 P(X 0) 5  ，P(X 1) 10 5  ，…………………………………………(9分) C3 91 C3 91 15 15 C2C1 45 C3 24 P(X 2) 10 5  ，P(X 3) 10  ， ………………………………………(11分) C3 91 C3 91 15 15 则X 的分布列为： …………………………………………………………………………(13分) X 0 1 2 3 2 20 45 24 P 91 91 91 91 20 45 24 故X 的数学期望为E(X)1 2 3 2.…………………………………(15分) 91 91 91 1 π 3 17.（1）由题知AB2，在MBO 中，OB1,MB ,MBO ，求得OM  ，则 2 3 2 BM2+OM2 BO2，ABOM ，…………………………………………………………(3分) π 又BOP ，AOOP,OAOBO ，故OP平面AOB，所以OP AB， ……(4分) 2 OPOM O，AB平面MOP；………………………………………………………(5分) （2）①设BOP,AOBO,AOOP，则二面角BAOP的平面角即为， …(6分) 1 3 在OB上取点N ，使ON 3NB，连接MN ，MN//OA，MN  OA ， 4 4 1 3 3 四棱锥 M OCPB 的体积V   S  S ，其中S 表示四边形OCPB 的面积，则 3 4 12 1 1 2  1 1  3 1  S  OPOBsin OPOCsin    sin   cos sin  2 2  3  2 2  2 2  3 3 3    sin cos sin   ，…………………………………………………(8分) 4 4 2  6  3   3 2   5 由 V  ， 可 得 sin  ， 0 ， 则   ， 故 16  6 2 3 6 6 6   2       ，解得  ,  ，即二面角BAOP的取值范围为  ,  ；…(10分) 3 6 3 6 2 6 2   ②以OB方向x轴正方向，在BOC 内垂直于OB的方向为y轴正方向，OA方向为z轴正 方 向 建 立 空 间 直 角 坐 标 系 ， 则 O(0,0,0) ， A(0,0, 3) ， B(1,0,0) ， P(cos,sin,0)， …………………………………………………………………………(12分)     1 AP(cos,sin, 3) ，OB(1,0,0)，cos cos AP,OB  cos ，……(13分) 2 7 {#{QQABBQAAggAIAJAAABhCAQngCkKQkBGCACoGBEAEoAIBSAFABAA=}#}   3 3   ,  ， cos0, ，即cos的最大值为 . ……………………………(15分) 6 2  2  4 c 2 c2 a2 b2 1 18.（1）依题意e  ，则   ，因此a2 2b2，……………………(2分) a 2 a2 a2 2 设AB:y x，A(x ,y ),B(x ,y )，联立AB与E 的方程得3x2 2b2， …………(3分) 1 1 1 1 1 又|AB| 1(1)2 |2x |4，即x2 2，…………………………………………………(4分) 1 1 y2 x2 故b2 3,a2 6，即椭圆E 的标准方程为E：  1；………………………………(6分) 6 3 （2）【解法1】设A(x ,y ),B(x ,y ),C(x ,y ),D(x ,y )，可知PA的斜率存在，设为k ，则 1 1 2 2 3 3 4 4 y 3 k  3 (x 0) ， PA 的 方 程 为 ykx3 ， 联 立 PA 与 E 的 方 程 ， 整 理 得 x 3 3 (k2 2)x2 6kx30，……………………………………………………………………(7分) 3 3 3x 3x x xx  ，则x   3  3  3 ，…(8分) 1 3 k2 2 1 (k2 2)x (y 3)2 2x 2 y 2 2x 2 6y 9 52y 3 3 3 3 3 3 3 125y x 125y 又y kx 3 3 ，故A( 3 , 3)， ……………………………………(9分) 1 1 52y 52y 52y 3 3 3 x 125y 同理可得B( 4 , 4)，易知CD的斜率不为0，设CD的方程为xmyn，则 52y 52y 4 4 x x (my n)(52y )(my n)(52y ) (5m2n)(y y ) x x  4  3  4 3 3 4  3 4 2 1 52y 52y (52y )(52y ) (52y )(52y ) 4 3 4 3 4 3 ………………………………………………………………………………………………(11分) 125y 125y y  y y y  4  3  3 4 ， ……………………………………(12分) 2 1 52y 52y (52y )(52y ) 4 3 4 3 y y y y 又k  2 1  3 4 1，则2n5m1，…………………………(13分) AB x x (5m2n)(y y ) 2 1 3 4 1 5 对比CD的方程可知，直线CD恒过定点Q( , )，……………………………………(14分) 2 2 2 1 5  2 设点P到直线CD的距离为d ，则d |PQ| ( 0)2  3  ， …………(16分) 2 2  2 2 当且仅当PQCD时，点P到直线CD的距离取到最大值 .………………………(17分) 2 8 {#{QQABBQAAggAIAJAAABhCAQngCkKQkBGCACoGBEAEoAIBSAFABAA=}#}    （2）【解法2】设A(x ,y ),B(x ,y ),C(x ,y ),D(x ,y )，APPC,BPPD， 1 1 2 2 3 3 4 4 x x y y 则0 1 3,3 1 3 ......①，……………………………………………………(7分) 1 1 y2 x2 y 2 x 2 2y 2 2x 2 又 1  1 1, 3  3 1，即 3  3 2， 6 3 6 3 6 3 1 y y y y 1 x x x x 作差整理得 ( 1 3)( 1 3) ( 1 3)( 1 3) 1，…………………………(8分) 6 1 1 3 1 1 y y 结合①，解得 1 3 1......②， ……………………………………………………(9分) 2(1) 5  5 1 由①②，解得y   ,y   ......③， ………………………………………(11分) 1 2 2 3 2 2 5  5 1 同理可得，x x 0,y   ,y   ......④， …………………………(12分) 2 4 2 2 2 3 2 2 可知CD的斜率不为0，设CD的方程为xmyn，结合①③④可得： y y y y y y  k  1 2  1 2  1 2  1 ， 则 AB x x x x (my n)(my n) (5m 2n)() 1 2 3 4 3 4 2n5m1， ………………………………………………………………………………(13分) 1 5 对比CD的方程可知，直线CD恒过定点Q( , )，……………………………………(14分) 2 2 2 1 5  2 设点P到直线CD的距离为d ，则d |PQ| ( 0)2  3  ， …………(16分) 2 2  2 2 当且仅当PQCD时，点P到直线CD的距离取到最大值 .………………………(17分) 2 （2）【解法 3】由题可设如下直线方程： PA:(y3)k x0 ， PB:(y3)k x0 ， 1 2 AB:(y3)xt 0(t 0) ，CD:m(y3)xn0(n0) ，则过 A,B,C,D四点的曲线 系方程为：[(y3)k x][(y3)k x][(y3)xt][m(y3)xn]0 ，……(9分) 1 2 则x项的系数为nt，(y3)项的系数为ntm，常数项为tn， ……………………(10分) 又椭圆E 的方程可写为：2x2 (y3)2 6(y3)30，……………………………(11分) nt 0  m1 5 1 对比系数可知：ntm ，解得n ，即CD:m(y )x 0， ………(13分)  2 2 2 2  tn 1 5 故直线CD恒过定点Q( , )，……………………………………………………………(14分) 2 2 2 1 5  2 设点P到直线CD的距离为d ，则d |PQ| ( 0)2  3  ， …………(16分) 2 2  2 2 当且仅当PQCD时，点P到直线CD的距离取到最大值 .………………………(17分) 2 9 {#{QQABBQAAggAIAJAAABhCAQngCkKQkBGCACoGBEAEoAIBSAFABAA=}#}  sinhx  'coshx 19.（1）①导数： ，证明如下：………………………………………(2分)   coshx  'sinhx    sinhx  '   ex ex    ex ex coshx,    2  2  ； ……………………………………………(4分)  ex ex   ex ex  coshx  '   sinhx   2  2 ②二倍角公式：cosh2x2coshx21，证明如下：…………………………………(2分) ex ex  2 e2x 2e2x e2x e2x 2coshx2 12  1 1 cosh 2x ； ………(4分)  2  2 2 ③平方关系： coshx 2  sinhx 2 1，证明如下： ……………………………………(2分) ex ex  2 ex ex  2 e2x e2x 2 e2x e2x 2  coshx 2  sinhx 2       1； (4分)  2   2  4 4 【说明：只需证到 1 个即给 4 分；证到其它性质如：①sinh(2x)2sinhxcoshx ；② cosh(2x)12sinhx2 ；③cosh(2x)coshx2sinhx2 也正确.】 （2）令F  x sinhxkx,x 0,，F x coshxk ， …………………………(6分) ex ex ①当k 1时，由coshx  exex 1 ，又因为x0，故ex ex，等号不成立， 2 所以F x coshxk 0 ，故F(x)为增函数， 此时 F(x)F(0)0 ，故对任意x0，sinhxkx恒成立，满足题意； ………………(7分) ②当k 1时，令GxFx,x0,，则G x sinhx0，可知Gx是增函数， 1 由G(0)1k 0与G(ln2k) 0可知，存在唯一x (0,ln2k) ，使得G(x )0，故 4k 0 0 当 x(0,x ) 时， F(x)G(x)G(x )0 ，则 F(x) 在 (0,x ) 上为减函数，故对任意 0 0 0 x(0,x )，F(x)F00，不合题意； 0 综上所述，实数k 的取值范围为,1 ； ………………………………………………(10分) ex ex （3）【解法 1】由a a 1，函数coshx 的值域为 1,，对于任意大于1的 1 2 实数a ，存在不为0的实数m，使得coshma ， ……………………………………(11分) 1 1 类 比 双 曲 余 弦 函 数 的 二 倍 角 公 式 cosh2x2coshx21 ， 由 coshma ， 1 10 {#{QQABBQAAggAIAJAAABhCAQngCkKQkBGCACoGBEAEoAIBSAFABAA=}#}a 2coshm21cosh(2m)，a cosh(22m)，猜想：a cosh  2n1m  ，………(12分) 2 3 n 由数学归纳法证明如下：①当n1时，a acosh  211m  coshm成立； 1 ②假设当nk（k 为正整数）时，猜想成立，即a cosh  2k1m  ，则 k a 2a 2 12cosh(2k1m) 2 1cosh(22k1m)cosh(2km)，符合上式， k1 k   综上：a cosh  2n1m  ，…………………………………………………………………(14分) n 若a cosh  22023m   17 ，设t 22023m，则cosht  et et  17 ，解得：et 4或 1 ， 2024 8 2 8 4 ln2 em em 1  1 1  即t ln4，故m ，则a coshm  222022 222022 ， ……(16分) 22022 1 2 2    1  1 1  17 综上：存在实数a 222022 222022 ，使得a  成立.…………………………(17分) 2  2024 8   （3）【解法 2】构造数列 x  ( x 0 )，且 a cosh(x ) ，a 2a 2 1 ， n n n n n1 n a 2coshx 21cosh(2x )，则 a n1 cosh(x n1 )cosh(2x n ) ， ……………(14分) n1 n n cosh(x) 在0,上单调递增，故 x 2x ，即x  是以 2 为公比的等比数列， n1 n n x  x 22023，ex 2024   ex 1 22023 ，ex 1   ex 2024  22 1 023 ， ……………………………(15分) 2024 1 a cosh(x ) 1 ex 2024 ex 2024   17 ，解得ex 2024 4或 1 ，…………………(16分) 2024 2024 2 8 4  1 1   1 1  1 1 1 故aa cosh(x ) (ex 1ex 1) 422023 422023  222022 222022  ， 1 1 2 2  2      1  1 1  17 综上：存在实数a 222022 222022 ，使得a  成立.…………………………(17分) 2  2024 8   命题：彭小奇（湘东中学） 黄贤锋（萍乡中学） 周昔康（莲花中学） 罗缘辉（芦溪中学） 刘 维（上栗中学） 审核：胡 斌（市教研室） 11 {#{QQABBQAAggAIAJAAABhCAQngCkKQkBGCACoGBEAEoAIBSAFABAA=}#}