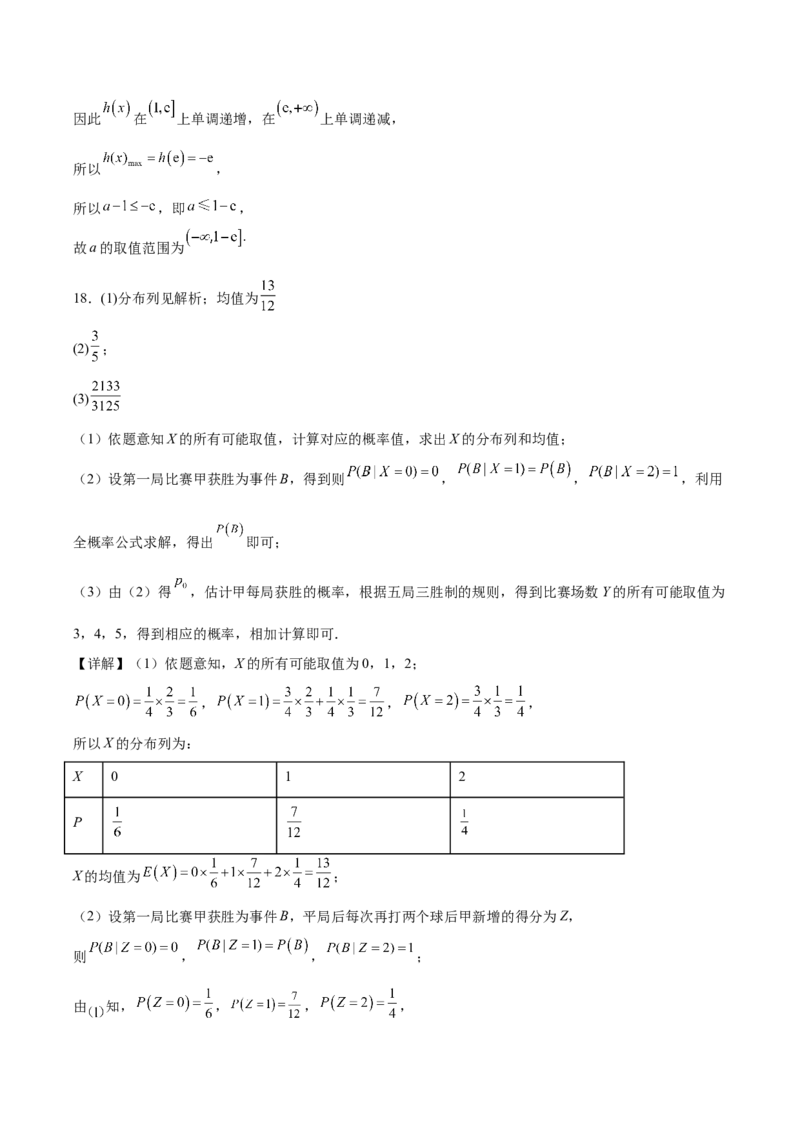文档内容
江苏省徐州市2024-2025学年高二下学期期中考试
数学试题
一、单选题
1.函数 在[0,π]上的平均变化率为
A.1 B.2 C.π D.
2.已知函数 上一点 ,则在点P处切线的斜率为( )
A. B. C.1 D.
3.已知 是一个随机试验中的两个事件,且 ,则 ( )
A. B. C. D.
4.已知随机变量X的概率分布如表所示,且 ,则 ( )
X 1 2 3
P n m
A. B. C. D.
5.甲、乙两人向同一目标各射击1次,已知甲命中目标的概率为 ,乙命中目标的概率为 ,已知目
标至少被命中1次,则甲命中目标的概率为( )
A. B. C. D.
6.已知 是定义在 上的奇函数,若对于任意的 ,都有 成立,
且 ,则不等式 解集为( )
A. B.
C. D.7.某校有5名学生打算前往观看电影《哪吒2》,《战狼》,《流浪地球2》,每场电影至少有1名学生
且至多2名学生前往,则甲同学不去观看电影《哪吒2》的方案种数有( )
A.30 B.45 C.60 D.75
8.以罗尔中值定理、拉格朗日中值定理、柯西中值定理为主体的“中值定理”反映函数与导数之间的重
要联系,是微积分学重要的理论基础,其中拉格朗日中值定理是“中值定理”的核心,其内容如下:如果
函数 在闭区间 上连续,在开区间 内可导,则 内至少存在一个点 ,使得
,其中 称为函数 在闭区间 上的“中值点”.请问函数
在区间 上的“中值点”的个数为( )
A.0 B.1 C.2 D.3
二、多选题
9.下列函数的导数运算正确的是( )
A. B.
C. D.
10.已知 ,其中 ,则( )
A. B.
C. D.
11.数学家棣莫弗发现,如果随机变量X服从二项分布 ,那么当n比较大时,X近似服从正态分布
,其密度函数为 , 任意正态分布 ,可通过变换
转化为标准正态分布 当 时,对任意实数x,记 ,则
( )A.当 时,
B.
C.随机变量 ,当 , 都减小时,概率 增大
D.随机变量 ,当 增大, 减小时,概率 保持不变
三、填空题
12.已知随机变量 ,若 , ,则 .
13.在如图所示的圆环形花园种花,将圆环平均分成A,B,C,D四个区域,现有牡丹、芍药、月季、玫
瑰、蝴蝶兰五种花可供选择,要求每个区域只种一种花且相邻区域的花不同,则不同的种植方法有
种.
14.若 恒成立,则实数 .
四、解答题
15.已知 的展开式中共有11项.
(1)求展开式中含 的项的系数; 结果用数字作答
(2)求二项式系数最大的项.
16.结合排列组合,解决下列问题 结果用数字作答
(1)将4封不同的信放到3个不同的信箱中,有多少种放法?
(2)将4封不同的信放到3个不同的信箱中,每个信箱至少有一封信,有多少种放法?
(3)将4封标有序号A,B,C,D的信放到四个标有A,B,C,D的信箱中,恰有一组序号相同,则有多少
种放法?
17.已知函数(1)若 ,求函数 的单调区间和极值;
(2)若存在 ,使得 成立,求a的取值范围.
18.11分制乒乓球比赛规则如下:在一局比赛中,每两球交换发球权,每赢一球得1分,先得11分且至
少2分领先者胜,该局比赛结束;当某局比分打成10:10后,每一球交换发球权,领先2分者胜,该局比
赛结束.现有甲、乙两人进行一场五局三胜且每局制的乒乓球比赛,比赛开始前通过抛掷一枚质地均匀的
硬币来确定谁先发球.假设甲发球时甲得分的概率为 ,乙发球时乙得分的概率为 ,各球的比赛结果相
互独立,且各局的比赛结果也相互独立.已知第一局目前比分为10:10,且接下来轮到甲发球.
(1)求再打两个球甲新增的得分X的分布列和均值;
(2)求第一局比赛甲获胜的概率 ;
(3)现用 估计每局比赛甲获胜的概率,求该场比赛甲获胜的概率.
19.若定义在 上的函数 和 分别存在导函数 和 ,且对任意实数 ,都存在常
数 ,使 成立,则称函数 是函数 的“ 控制函数”,称 为控制系数.
(1)求证:函数 是函数 的“ 控制函数”;
(2)若函数 是函数 的“ 控制函数”,求控制系数 的取值范围;
(3)若函数 ,函数 为偶函数,函数 是函数 的“ 控制函数”,求
证:“ ”的充要条件是“存在常数 ,使得 恒成立”.题号 1 2 3 4 5 6 7 8 9 10
答案 C B D B C D C C AD ACD
题号 11
答案 BD
1.C
根据平均变化率的公式,计算出平均变化率.
【详解】平均变化率为 .
故选:C
2.B
求导函数,把点的横坐标代入导函数即可求解.
【详解】由 ,
可得 ,
故在点P处切线的斜率为
故选:B
3.D
利用条件概率公式的变式公式和对立事件的概率计算,就可以求出结果.
【详解】因为 ,由对立事件概率计算公式可得: ,
则 ,
故选:D.
4.B
利用分布列的性质以及期望公式列方程组即可求解.
【详解】由分布列的性质可得, ,所以 ,
又因为 ,所以 ,即 ;
联立方程 ,解得 ,所以
故选:B
5.C
根据条件概率知识可解.
【详解】设事件 “甲命中目标”, “至少命中一次”,
则 , ,
则已知目标至少被命中1次,则甲命中目标的概率为
故选:C
6.D
设函数 ,结合导数与单调性关系先判断 的单调性,然后判断奇偶性,即可求解.
【详解】设函数 ,则 ,
因为 是 上的奇函数,所 ,
所以 是 上的偶函数, ,
因为当 时, ,
所以 ,即 在 上单调递减,
因此 在 上单调递增,
所以 , ,
当 ,原不等式可化为 ,即 ,解得 ,
当 ,原不等式可化为 ,即 ,解得 ,
综上所述, .
故选:D7.C
先分组,分配的时候考虑甲的特殊情况,即可求解.
【详解】依题意,将5名学生分为1,2,2三组,即第一组1个人,第二组2个人,第三组2个人,共有
种方法;
由于甲同学不去观看电影《哪吒2》,故甲所在的组只有2种选择,剩下的2组任意选,所以由 种
方法;
按照分步乘法原理,共有 种方法.
故选:C
8.C
先对函数求导,结合已知定义即可求解.
【详解】因为 , ,
所以 , , ,
若 ,
由 ,解得
故选:C
9.AD
利用导数公式表计算可得A正确,由于 为常数,所以其导数为0,即B错误,根据乘法运算法则求导
可知C错误,再由复合函数求导计算可得D正确.
【详解】易知 ,可得A正确;
又 ,即B错误;
易知 ,C错误;
显然 ,D正确.
故选:AD10.ACD
利用二项式定理,结合赋值法,逐项判断即可.
【详解】对于A, ,其中 , ,解得 ,A正确;
对于B, 项的系数为 ,B错误;
对于C,令 ,得 ,令 ,得 ,
因此 ,C正确;
对于D,令 ,得 ,
由选项C得 ,D正确.
故选:ACD
11.BD
由定义即可判断A;根据 结合正态曲线的对称性,可判断B;根据正态分布的 准则可判
断CD.
【详解】对于A:当 时,
,故A错误;
对于B:根据正态曲线的对称性可得: ,即
,故B正确;
对于CD:根据正态分布的 准则,在正态分布中 代表标准差, 代表均值, 即为图象的对称轴,
根据 原则可知X数值分布在 的概率是常数,故由 可知,
D正确,C错误.
故选:BD.
12. /
根据二项分布的期望公式和方差公式求解.【详解】因为随机变量 ,
所以 , ,
联立解得
故答案为:
13.260
根据题意可分若A和C相同,B和D相同时,若种三种花,若种四种花,三种情况讨论即可.
【详解】解:现有牡丹、芍药、月季、玫瑰、蝴蝶兰五种花可供选择,要求每个区域只种一种花且相邻区
域的花不同,
则四个区域最少两种花,最多4种花.所以分三类:
若A和C相同,B和D相同时,有 种方法;
若种三种花,分A和C相同与不同两种情况,此时有 种;
若种四种花,则有 种,
则不同的种植方法有 种.
故答案为: .
14. /
设 ,则原式等价于 ,进而得到 恒成立,再根据切线不等式得
解.
【详解】因为 恒成立,即 恒成立,
即 恒成立,
设 ,则 恒成立,
又 ,则 在 上单调递增,
可得 恒成立,即 恒成立,令 ,则 ,所以当 时 ,当 时 ,
所以 在 上单调递增,在 上单调递减,所以 ,
即 恒成立(当且仅当 时取等号),
所以 ,解得
故答案为:
15.(1)960;
(2)
(1)结合二项式定理通项计算,即可求解;
(2)结合(1)的通项公式以及二项式系数的增减性,即可求解.
【详解】(1)由题意可知 ,解得 ,
展开式的通项为 ,
令 ,解得 ,
故展开式中含 的项的系数为 ;
(2)由 可得二项式系数最大的项为第六项,
即 .
16.(1)81;
(2)36;
(3)
(1)根据分步乘法计数原理可解;
(2)根据题意将4封信分成1,1,2三组,再分到3个信箱即可;
(3)确定一组序号相同,而其余的全部不同均有2种情况,从而可解.
【详解】(1)将4封不同的信放到3个不同的信箱中,有 种放法;
(2)将4封不同的信放到3个不同的信箱中,每个信箱至少有一封信,则将4封信分成1,1,2三组,有 组,再分给三个信箱,有 种放法;
(3)将4封标有序号A,B,C,D的信放到四个标有A,B,C,D的信箱中,
先确定一组序号相同有 种情况,其余的全部不同均有2种情况,则共有 种情况.
17.(1)增区间为 和 ,减区间为 ,极大值 ,极小值 ;
(2)
将 代入函数解析式,利用导数判断其单调性和极值即可;
问题等价于存在 , ,设 ,利用导数求函数 在 上的最大值,
进而可得出答案.
【详解】(1)若 ,则 ,
则 ,
令 ,可得 或 ;令 ,可得 ,
所以该函数增区间为 和 ,减区间为 ,
当 时取得极大值 ,当 时取得极小值 ;
(2)因为存在 ,有 成立,
所以存在 ,有 成立,即存在 ,
因为 ,所以存在 , ,
设 ,其中 ,则 ,
因为 ,所以 ,
当 时, ,因此 在 上单调递增,在 上单调递减,
所以 ,
所以 ,即 ,
故a的取值范围为
18.(1)分布列见解析;均值为
(2) ;
(3)
(1)依题意知X的所有可能取值,计算对应的概率值,求出X的分布列和均值;
(2)设第一局比赛甲获胜为事件B,得到则 , , ,利用
全概率公式求解,得出 即可;
(3)由(2)得 ,估计甲每局获胜的概率,根据五局三胜制的规则,得到比赛场数Y的所有可能取值为
3,4,5,得到相应的概率,相加计算即可.
【详解】(1)依题意知,X的所有可能取值为0,1,2;
, , ,
所以X的分布列为:
X 0 1 2
P
X的均值为 ;
(2)设第一局比赛甲获胜为事件B,平局后每次再打两个球后甲新增的得分为Z,
则 , , ;
由 知, , , ,由全概率公式得,
,
解得 ,即第一局比赛甲获胜的概率 ;
(3)由(2)知 ,所以估计甲每局获胜的概率均为 ,
根据五局三胜制的规则,设甲获胜时的比赛总局数为Y,
因为每局的比赛结果相互独立,所以Y的所有可能取值为3,4,5,
所以 , , ;
所以该场比赛甲获胜的概率为
19.(1)证明见解析
(2)
(3)证明见解析
【详解】(1)因为 , ,所以 , ,则 ,
故 ,即 恒成立,
故函数 是函数 的“ 控制函数”.
(2)因为 , ,
则 , ,
因为函数 是函数 的“ 控制函数”,
所以,对任意的 , ,则 ,令 ,
则
,
且 ,
故当 时, ,当 时, ,
即 在 上单调递减,在 上单调递增,
所以, ,所以 ,
若函数 是函数 的“ 控制函数”,
则实数 的取值范围是 .
(3)充分性:若存在常数 使得 恒成立,则 ,
因为函数 为偶函数,所以 ,则 ,
则 为偶函数,即 ,
所以 恒成立,所以 ;
必要性:若 ,则 ,所以函数 为偶函数,
函数 是函数 的“ 控制函数”,
因此对任意的 , ,
又 , ,所以, , ,所以 ,即 ,
用 代换 可得 ,故 ,
综上可知 ,记 ,则 ,
因此存在常数 使得 恒成立,
综上可得,“ ”的充要条件是“存在常数 使得 恒成立”.