文档内容
安徽省“鼎尖教育”2025 届高三 11 月份联考数学试题
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知集合 , ,则
M={x|√x−1<2} N={x|x2−x−2<0} M∩N=
A. {x|−1−1) (0,f(0)) x+2y+5=0 a
值为
A. 1 B. −1 C. 3 D. −3
4.已知 (π ), ( π),则
α∈ ,π √2cos2α=sin α− sin2α=
2 4
1 1 3 3
A. − B. C. − D.
4 4 4 4
3
{log (2x−1)+ ,x≥1,
5.已知函数 a 2 在 上单调递减,则 的取值范围为
f(x)= (0,+∞) a
2a
x+ ,00,b>0,且a+b=4,则
1 1
A. + ≥1 B. √a+√b≥2√2
a b
C. D. ( 2)( 2)
a2+2b≥8 a+ b+ ≥8
b a
10.已知函数 , , 恒成立,则
f(x)=x(ex−e−x ) ∀θ∈R f(3t+tcosθ−2−sinθ)≤f(2+sinθ)
A. f(x)是偶函数
B. f(x)在(0,+∞)上单调递增
1
C. t可以取
3
D. 当 t= √2时, f(3t+tcosθ−2−sinθ) 的取值范围是 [ e− 1 ,2 ( e2− 1 ) ]
4 e e2
第 页,共 页
2 11
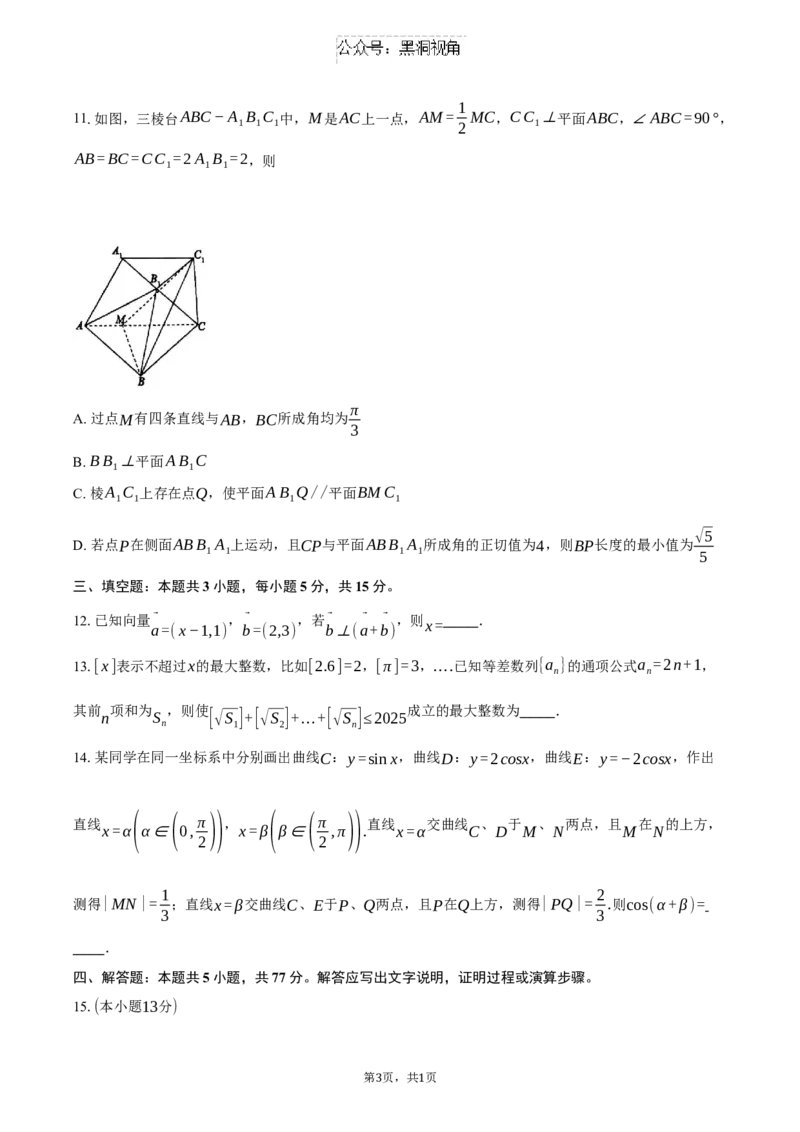
11.如图,三棱台ABC−A B C 中,M是AC上一点,AM= MC,CC ⊥平面ABC,∠ABC=90°,
1 1 1 2 1
AB=BC=CC =2A B =2,则
1 1 1
π
A. 过点M有四条直线与AB,BC所成角均为
3
B. BB ⊥平面AB C
1 1
C. 棱A C 上存在点Q,使平面AB Q//平面BMC
1 1 1 1
√5
D. 若点P在侧面ABB A 上运动,且CP与平面ABB A 所成角的正切值为4,则BP长度的最小值为
1 1 1 1 5
三、填空题:本题共3小题,每小题5分,共15分。
12.已知向量⃗
a=(x−1,1)
,⃗
b=(2,3)
,若⃗
b⊥(
⃗
a+
⃗
b)
,则
x=
.
13.[x]表示不超过x的最大整数,比如[2.6]=2,[π]=3,….已知等差数列{a }的通项公式a =2n+1,
n n
其前 项和为 ,则使 成立的最大整数为 .
n S [√S ]+[√S ]+…+[√S ]≤2025
n 1 2 n
14.某同学在同一坐标系中分别画出曲线C:y=sinx,曲线D:y=2cosx,曲线E:y=−2cosx,作出
直线 ( ( π)), ( (π )) 直线 交曲线 、 于 、 两点,且 在 的上方,
x=α α∈ 0, x=β β∈ ,π . x=α C D M N M N
2 2
1 2
测得|MN|= ;直线x=β交曲线C、E于P、Q两点,且P在Q上方,测得|PQ|= .则cos(α+β)=
3 3
.
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.(本小题13分)
第 页,共 页
3 1π
记△ABC内角A,B,C的对边分别为a,b,c,已知sin2A=cos2B,且A>B≥ .
4
(1)求A−B的值;
(2)若a=√2b=2,求△ABC的面积.
16.(本小题15分)
{x+4
已知函数
,(x<0且x≠−3),
f(x)= x+3
f(x−3),(x>0).
(1)求函数f(x)在区间(0,3)上的解析式;
(2)已知点A(2,−1),点M是函数f(x)在区间(0,3)上的图象上的点,求|MA|的最小值.
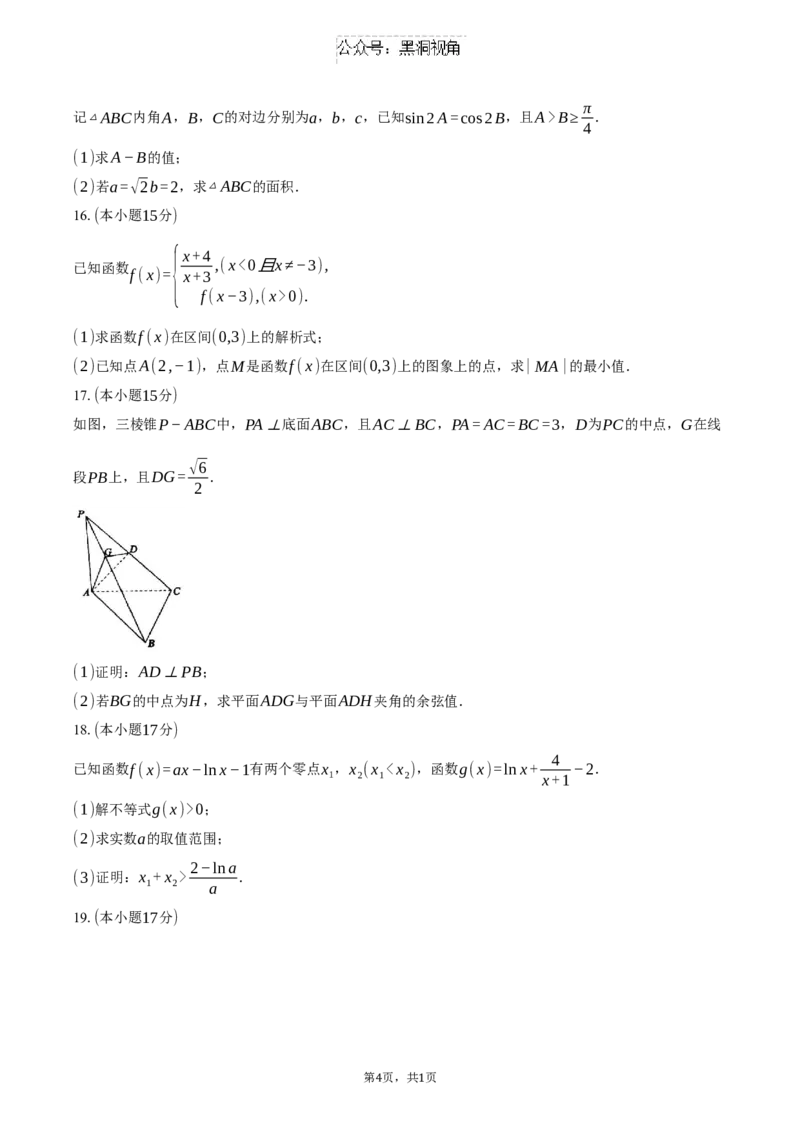
17.(本小题15分)
如图,三棱锥P−ABC中,PA⊥底面ABC,且AC⊥BC,PA=AC=BC=3,D为PC的中点,G在线
√6
段PB上,且DG= .
2
(1)证明:AD⊥PB;
(2)若BG的中点为H,求平面ADG与平面ADH夹角的余弦值.
18.(本小题17分)
4
已知函数f(x)=ax−lnx−1有两个零点x ,x (x 0;
(2)求实数a的取值范围;
2−lna
(3)证明:x +x > .
1 2 a
19.(本小题17分)
第 页,共 页
4 11
a =
1 n 1
1 a = 1+
1 a = 3 1 1
定义数列{a }为“阶梯数列”:a = , 2 1, 1+ ,……, 1+ .
n 1 1 1+ 1 …
1 1+
1 1
1+
1
(1)求“阶梯数列”中,a 与a 的递推关系;
n+1 n
(2)证明:对k∈N❑∗,数列{a2k−1}为递减数列;
证明: 1 (4) k−1.
(3) |a −a |≤ ⋅
k+1 k 2 9
第 页,共 页
5 1参考答案
1.D
2.A
3.C
4.C
5.D
6.B
7.B
8.A
9.AD
10.ABC
1.ACD
12.−7
13.63
−2√451−2
14.
45
π
15.(1)sin2A=cos2B=sin( −2B),
2
π π
故2A= −2B或2A+ −2B=π,
2 2
π π
当2A= −2B时,A= −B≤0不合题意,
2 4
π π
故2A+ −2B=π⇒A−B= ;
2 4
π
(2)a=√2b⇒sin A=√2sinB,即sin(B+ )=√2sinB,
4
√2 √2
∴ sinB+ cosB=√2sinB⇒sinB=cosB,
2 2
第 页,共 页
6 1π 3π π π π
∵ ≤B< ,∴B= ,故A= ,C= ,
4 4 4 2 4
1 1 √2
故S = absinC= ×2×√2× =1.
△ABC 2 2 2
16.解:(1)由题可知在(0,3)上,f(x)=f(x−3),
x−3+4 x+1
而x−3<0,所以f(x−3)= = ,
x−3+3 x
x+1
即在(0,3)上,f(x)= ;
x
(2)设M(x ,y ),
0 0
x +1 1 1 1 1 1
|MA|2=(x −2) 2+(y +1) 2=(x −2) 2+( 0 +1) 2=(x2+ )+4( −x )+8=( −x ) 2+4( −x )+10=( −x +2) 2+6≥6
0 0 0 x 0 x2 x 0 x 0 x 0 x 0
0 0 0 0 0 0
1
当且仅当 −x +2=0时,取得等号,解得x =√2+1∈(0,3),
x 0 0
0
故|MA|的最小值为√6
17.解:(1)证明:因为PA⊥底面ABC,且BC⊂底面ABC,
所以PA⊥BC,
因为PA∩AC=A,且PA,AC⊂平面PAC,AC⊥BC,
所以BC⊥平面PAC,
又因为AD⊂平面PAC,所以BC⊥AD,
因为PA=AC,且D为PC的中点,
所以AD⊥PC,
又因为PC∩BC=C,且PC,BC⊂平面PBC,
所以AD⊥平面PBC,
因为PB⊂平面PBC,所以AD⊥PB;
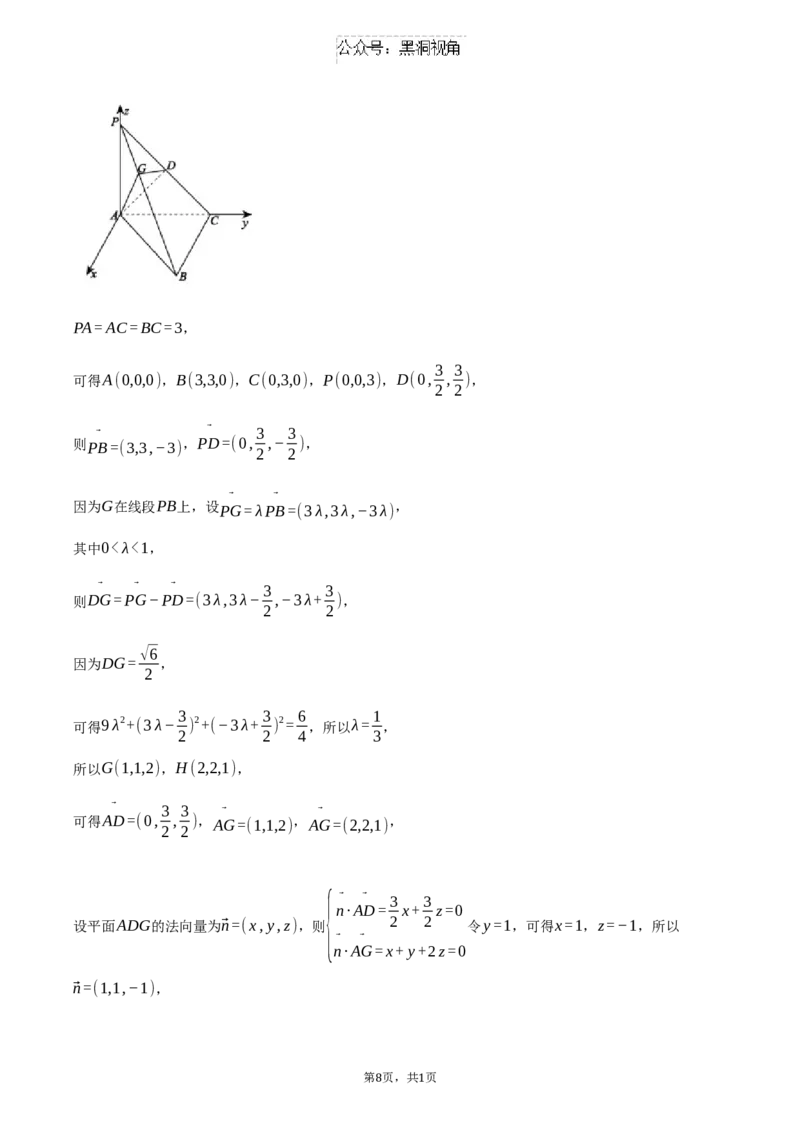
(2)根据题意可知,以点A为原点,以过点A且平行于BC的直线为x轴,
AC,AP所在的直线分别为y轴和z轴,建立空间直角坐标系,如图所示,
第 页,共 页
7 1PA=AC=BC=3,
3 3
可得A(0,0,0),B(3,3,0),C(0,3,0),P(0,0,3),D(0, , ),
2 2
⃗ ⃗ 3 3
则PB=(3,3,−3) ,PD=(0, ,− ),
2 2
⃗ ⃗
因为G在线段PB上,设PG=λPB=(3λ,3λ,−3λ) ,
其中0<λ<1,
⃗ ⃗ ⃗ 3 3
则DG=PG−PD=(3λ,3λ− ,−3λ+ ),
2 2
√6
因为DG= ,
2
3 3 6 1
可得9λ2+(3λ− ) 2+(−3λ+ ) 2= ,所以λ= ,
2 2 4 3
所以G(1,1,2),H(2,2,1),
⃗ 3 3 ⃗ ⃗
可得AD=(0, , ),AG=(1,1,2) ,AG=(2,2,1) ,
2 2
{ ⃗ ⃗ 3 3
n·AD= x+ z=0
设平面ADG的法向量为⃗n=(x,y,z),则 2 2 令y=1,可得x=1,z=−1,所以
⃗ ⃗
n·AG=x+ y+2z=0
⃗n=(1,1,−1),
第 页,共 页
8 1{ ⃗ ⃗ 3 3
m⋅AD= y+ z=0
1
设平面ADH的法向量为m ⃗ =(x,y,z) ,则 2 2 令y=1,可得x=−
2
,z=−1,所以
⃗ ⃗
m⋅AH=2x+2y+z=0,
⃗ 1
m=(− ,1,−1),
2
设平面ADG与平面ADH的夹角为θ,
3
⃗ ⃗
|n⋅m| 2 √3
可得cosθ= = = ,
⃗ |⃗| 3 3
|n|⋅m √3×
2
√3
故平面ADG与平面ADH夹角的余弦值为 .
3
18. 1 4 (x−1) 2 ,
(1)g′(x)= − = ≥0
x (x+1) 2 x(x+1) 2
故g(x)为(0,+∞)上的增函数,
由题可知g(1)=0,g(x)>0,即g(x)>g(1),
∴g(x)>0的解集为(1,+∞).
1
(2)f ′(x)=a− ,
x
当a≤0时,f ′(x)<0,f(x)为减函数,不符合题意;
1 1
当a>0时,x∈(0, )时,f ′(x)<0,x∈( ,+∞)时,f ′(x)>0.
a a
又x→0时,f(x)→+∞;x→+∞时,f(x)→+∞.
1 1 1
∵f(x)有两个零点,故f( )=1−ln −1=−ln =lna<0,
a a a
解得0lna+1①
1 1
同理:ax =lnax +1−lna,
2 2
2(ax −1),
lnax > 2
2 ax +1
2
可化为 ,
a2x2+(alna−2a)x >−lna−1②
2 2
得:
②+① a2 (x2−x2 )+(alna−2a)(x −x )>0
2 1 2 1
2−lna
化简得:x +x > .
1 2 a
1
19.(1)由阶梯数列的形式结构可知a = ;
n+1 1+a
n
1 1 1 1
(2)a −a = − = −
2k+1 2k−1 1+a 1+a 1 1
2k 2k−2 1+ 1+
1+a 1+a
2k−1 2k−3
第 页,共 页
10 11+a 1+a a −a ,
= 2k−1− 2k−3= 2k−1 2k−3
2+a 2+a (2+a )(2+a )
2k−1 2k−3 2k−1 2k−3
a −a 1 ,
∴ 2k+1 2k−1 = >0
a −a (2+a )(2+a )
2k−1 2k−3 2k−1 2k−3
同理a −a , ,a −a ,
2k−1 2k−3>0
⋯⋯
5 3>0
a −a a −a
2k−3 2k−5 3 1
累乘得a −a a −a a −a ,
2k+1 2k−1
⋅
2k−1 2k−3
⋅⋯⋯
5 3>0
a −a a −a a −a
2k−1 2k−3 2k−3 2k−5 3 1
即a −a ,
2k+1 2k−1>0
a −a
3 1
2 1
a −a = −1=− <0,
3 1 3 3
∴a −a <0,
2k+1 2k−1
故对k∈N∗,{a }为递减数列;
2k−1
1 1 a −a
(3)a −a = − = k k+1
k+2 k+1 1+a 1+a (1+a )(1+a )
k+1 k k+1 k
|a −a | 1 ,
k+2 k+1 =
|a −a | (1+a )(1+a )
k+1 k k+1 k
又对 k∈N∗ , a −a = 1 − 1 = a 2k−1 −a 2k+1 ,
2k+2 2k 1+a 1+a (1+a )(1+a )
2k+1 2k−1 2k+1 2k−1
由(2)知a −a >0,
2k−1 2k+1
第 页,共 页
11 11
故a >a ⇒a >a >⋯>a = ,
2k+2 2k 2k 2k−2 2 2
1 1 2 1
a = > = >
又 2k+1 1+a 1 3 2,
2k 1+
2
1
故对n∈N∗,a > ,
n 2
|a −a | 1 1 4
∴ k+2 k+1 = < =
|a −a | (1+a )(1+a ) 1 9,
k+1 k k+1 k (1+ ) 2
2
|a −a | |a −a | |a −a | 4
∴ k+1 k ⋅ k k−1 ⋯⋯ 3 2 <( ) k−1
|a −a | |a −a | |a −a | 9
k k−1 k−1 k−2 2 1
4 1 4
∴|a −a |<|a −a |⋅( ) k−1= ⋅( ) k−1 (k≥2),
k+1 k 2 1 9 2 9
1
当k=1时,|a −a |= ,
2 1 2
1 4
综上,|a −a |≤ ⋅( ) k−1.
k+1 k 2 9
第 页,共 页
12 1