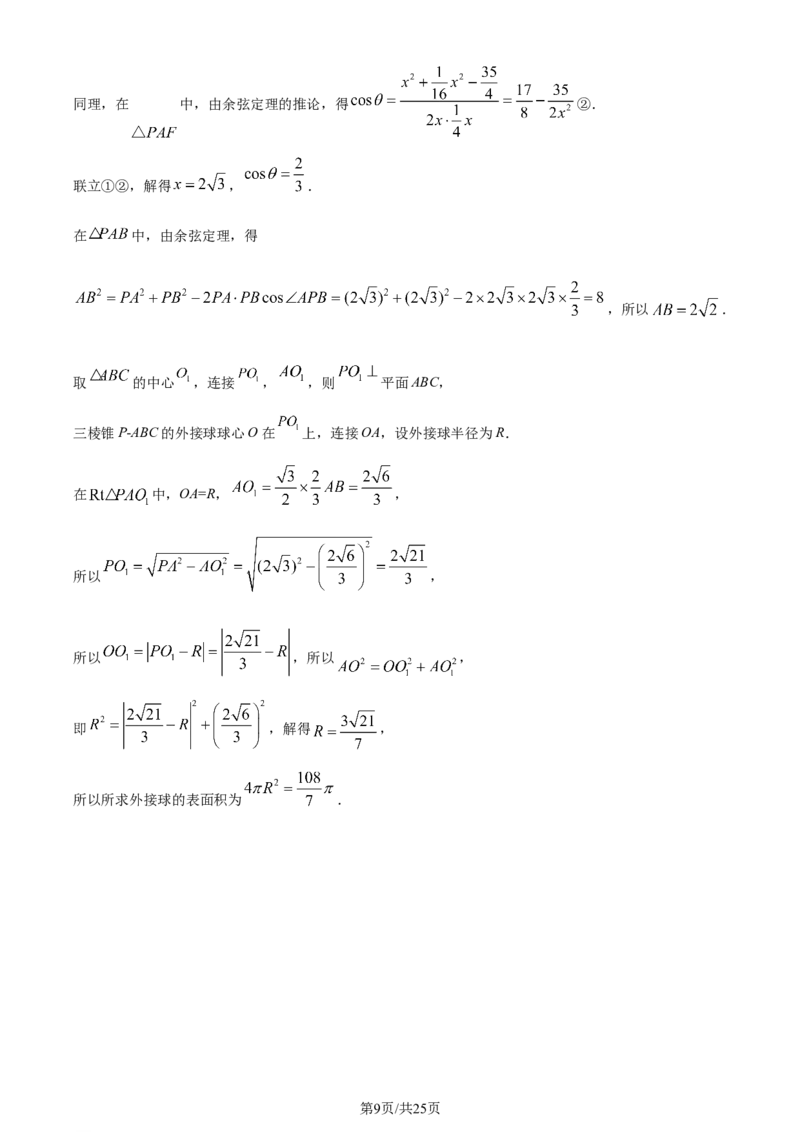文档内容
棠湖中学高 2021 级高三 10 月考试
数学(理工类)
本试卷共4页,23小题,满分150分.考试用时120分钟.
第I卷 选择题(60分)
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项
是符合题目要求的.
1. 若集合 ,则
A. B. C. D.
【答案】B
【解析】
【详解】 由题意,集合 ,
所以 ,故选B.
2. 下列函数中,在区间 上单调递增的是( )
A. B. C. D.
【答案】D
【解析】
【分析】由二次函数,分式函数,指数函数,对数函数的函数特征分别讨论单调区间可求解.
【详解】选项A是开口向下,对称轴为x=0的二次函数,所以在 是单调递减,不符.
选项B为分式函数,定义域为 ,所以只有两个减区间,也不符,
选项C是底数属于(0,1)的指数函数,所以在R上单调递减,不符.
选项D是定义在 上以10为底的对数函数,所以在 上单调递增,符合,
故选:D.
3. 已知 ,条件 ,条件 ,则 是 的( )
第1页/共25页
学科网(北京)股份有限公司A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件
【答案】A
【解析】
【分析】利用基本不等式证明充分性,利用特殊值证明必要性不成立,即可判断;
【详解】解:因 ,由 ,得: ,则
,当且仅当 时取等号,因此 推得出 ,即充分性
成立,
取 ,满足 ,但 ,即 推不出 ,即必要性不成立,所以 是
的充分不必要条件,
故选 :A
4. 古代人家修建大门时,贴近门墙放置两个石墩.石墩其实算是门墩,又称门枕石,在最初的时候起支撑
固定院门的作用,为的是让门栓基础稳固,防止大门前后晃动.不过后来不断演变,一是起到装饰作用,二
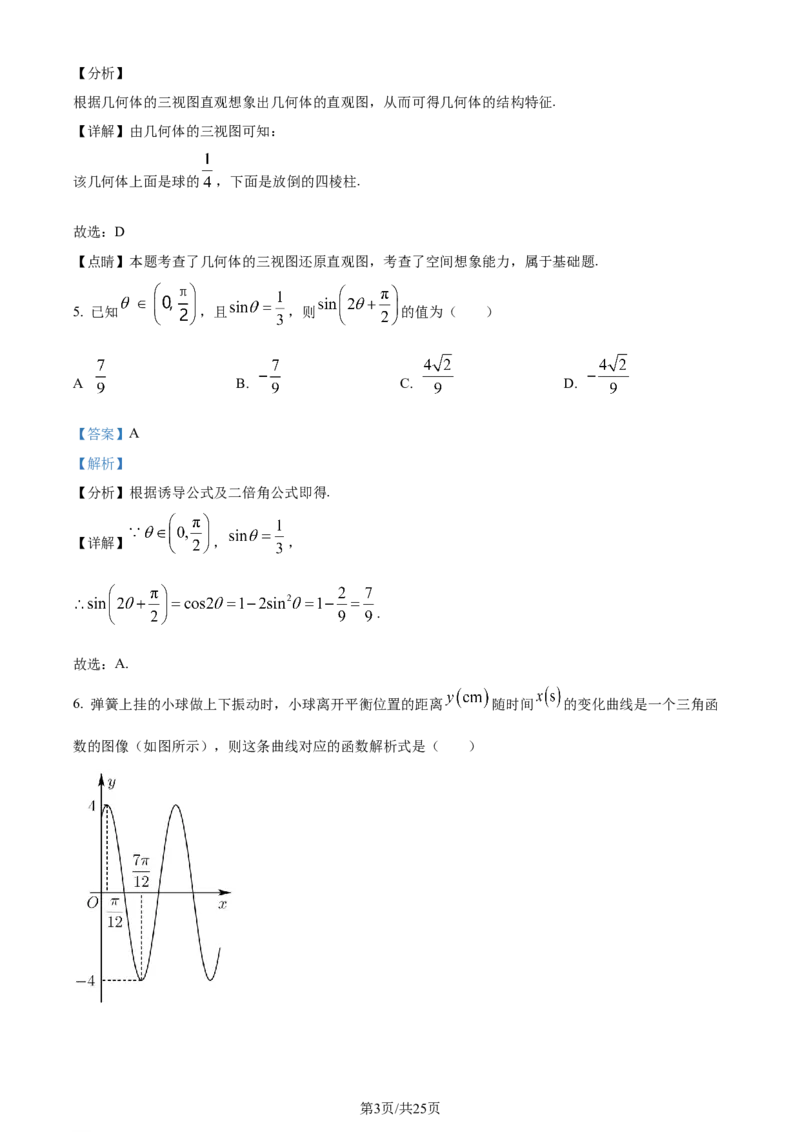
是寓意“方方圆圆”.如图所示,画出的是某门墩的三视图,则该门墩从上到下分别是( )
A. 半圆柱和四棱台 B. 球的 和四棱台
C. 半圆柱和四棱柱 D. 球的 和四棱柱
【答案】D
【解析】
第2页/共25页
学科网(北京)股份有限公司【分析】
根据几何体的三视图直观想象出几何体的直观图,从而可得几何体的结构特征.
【详解】由几何体的三视图可知:
该几何体上面是球的 ,下面是放倒的四棱柱.
故选:D
【点睛】本题考查了几何体的三视图还原直观图,考查了空间想象能力,属于基础题.
5. 已知 ,且 ,则 的值为( )
.
A B. C. D.
【答案】A
【解析】
【分析】根据诱导公式及二倍角公式即得.
【详解】 , ,
.
故选:A.
6. 弹簧上挂的小球做上下振动时,小球离开平衡位置的距离 随时间 的变化曲线是一个三角函
数的图像(如图所示),则这条曲线对应的函数解析式是( )
第3页/共25页
学科网(北京)股份有限公司A.
B.
C.
D.
【答案】A
【解析】
【分析】由函数 的部分图像得到 或 ,并分别讨论 或 时 的解析式
【详解】解:设该曲线对应的函数解析式为 ,
由图可知, 或 , ,则 ,
当 时, ,
由 ,解得 ,
因为 ,所以 ,所以 ;
当 时, ,
由 ,解得 ,
因为 ,所以 ,所以 ;
故选:A
7. 方程 的两根为 , ,且 ,则
第4页/共25页
学科网(北京)股份有限公司A. B. C. D. 或
【答案】B
【解析】
【分析】
利用韦达定理求出 与 的值,由两角和的正切公式求得 ,从而可得
结果.
【详解】∵方程 的两根为 , ,且 ,
∴ , ,再结合 ,故 ,
,
∴ ,故 .
又 ,∴ ,故选B.
【点睛】三角函数求值有三类,(1)“给角求值”:一般所给出的角都是非特殊角,从表面上来看是很难的,
但仔细观察非特殊角与特殊角总有一定关系,解题时,要利用观察得到的关系,结合公式转化为特殊角并
且消除非特殊角的三角函数而得解.(2)“给值求值”:给出某些角的三角函数式的值,求另外一些角的三角
函数值,解题关键在于“变角”,使其角相同或具有某种关系.(3)“给值求角”:实质是转化为“给值求值”,
先求角的某一函数值,再求角的范围,确定角.
8. 将函数 的图象向右平移 个单位长度,再将所得图象上所有点的横坐标变为原来的 (
)倍(纵坐标不变),得到函数 的图象,若函数 在区间 上是增函数,则 的取值范围
是( )
A. B. C. D.
第5页/共25页
学科网(北京)股份有限公司【答案】B
【解析】
【分析】先根据图象变换求解出 的解析式,然后结合正弦函数的单调增区间以及 的周期 的范
围,列出关于 的不等式组并求解出 的取值范围.
【详解】将函数 的图象经过变化后得到 的图象,
令 ( ),即 ( ),
∵ 在 上是增函数,∴ ,
又 ,∴ ,
令 时 ,解得 ,当 且 时,不符合题意,
故选:B.
【点睛】思路点睛:已知正、余弦型函数 (或 )的单调区间求解参
数范围的步骤:
(1)根据函数以及单调性列出关于 的不等式;
(2)将单调区间的端点值代入关于 的不等式中,同时注意到单调区间的长度不会超过半个周期
;
(3)由(1)(2)列出关于参数的所有不等式,由此求解出参数范围.
9. 函数 ,则 ( )
第6页/共25页
学科网(北京)股份有限公司A. 0 B. C. 4 D. 1
【答案】C
【解析】
【分析】首先设 ,则 ,根据对数的运算法则知 ,
再计算 即可.
【详解】设 ,
因为
.
所以
.
故选:C
【点睛】本题主要考查对数的运算,熟练掌握对数的运算法则为解题的关键,属于中档题.
10. 设 , , ,则( )
A. B. C. D.
【答案】B
【解析】
【分析】首先构造函数 ,利用导数判断函数的单调性,再利用 ,判断函数值的
大小,即可判断选项.
【详解】 , , ,
第7页/共25页
学科网(北京)股份有限公司设 , 且 ,令 ,得 ,
当 时, ,函数单调递减,当 时, ,函数单调递增,
因为 ,且 ,
所以 ,即.
故选:B
11. 在正三棱锥P-ABC中,D,E分别为侧棱PB,PC的中点,若 ,且 ,则三棱锥P-
ABC外接球的表面积为( )
A. B. C. D.
【答案】C
【解析】
【分析】结合题意,利用三角形相似得到 ,取线段PE的中点F,连接DF,AF,利用余
弦定理和勾股定理求出外接球半径,代入外接球的表面积公式即可求解.
【详解】如图,因为P-ABC为正三棱锥,所以 , .
取线段PE的中点F,连接DF,AF,因为D为PB的中点,所以 , .因为
AD⊥BE,所以 .在 中, ,
由勾股定理,得 .设 ,PA=x,
在 中,由余弦定理的推论,得 ①.
第8页/共25页
学科网(北京)股份有限公司同理,在 中,由余弦定理的推论,得 ②.
联立①②,解得 , .
在 中,由余弦定理,得
,所以 .
取 的中心 ,连接 , ,则 平面ABC,
三棱锥P-ABC的外接球球心O在 上,连接OA,设外接球半径为R.
在 中,OA=R, ,
所以 ,
所以 ,所以 ,
即 ,解得 ,
所以所求外接球的表面积为 .
第9页/共25页
学科网(北京)股份有限公司故选:C.
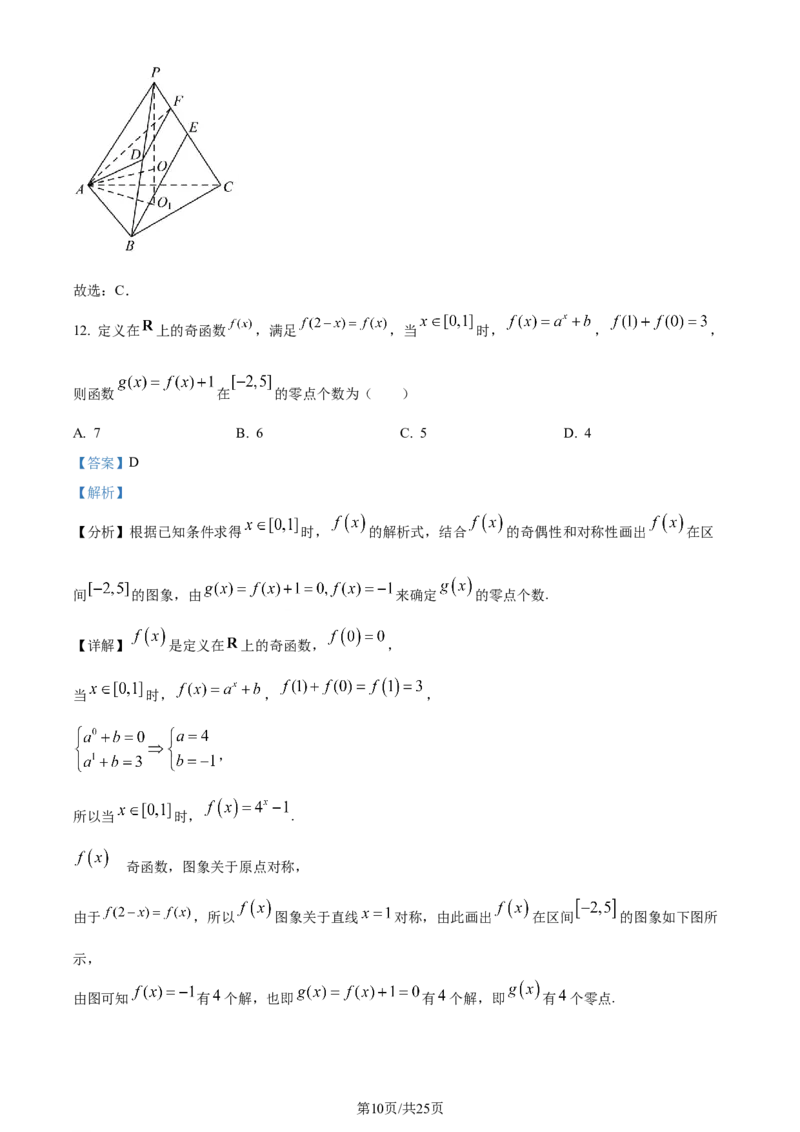
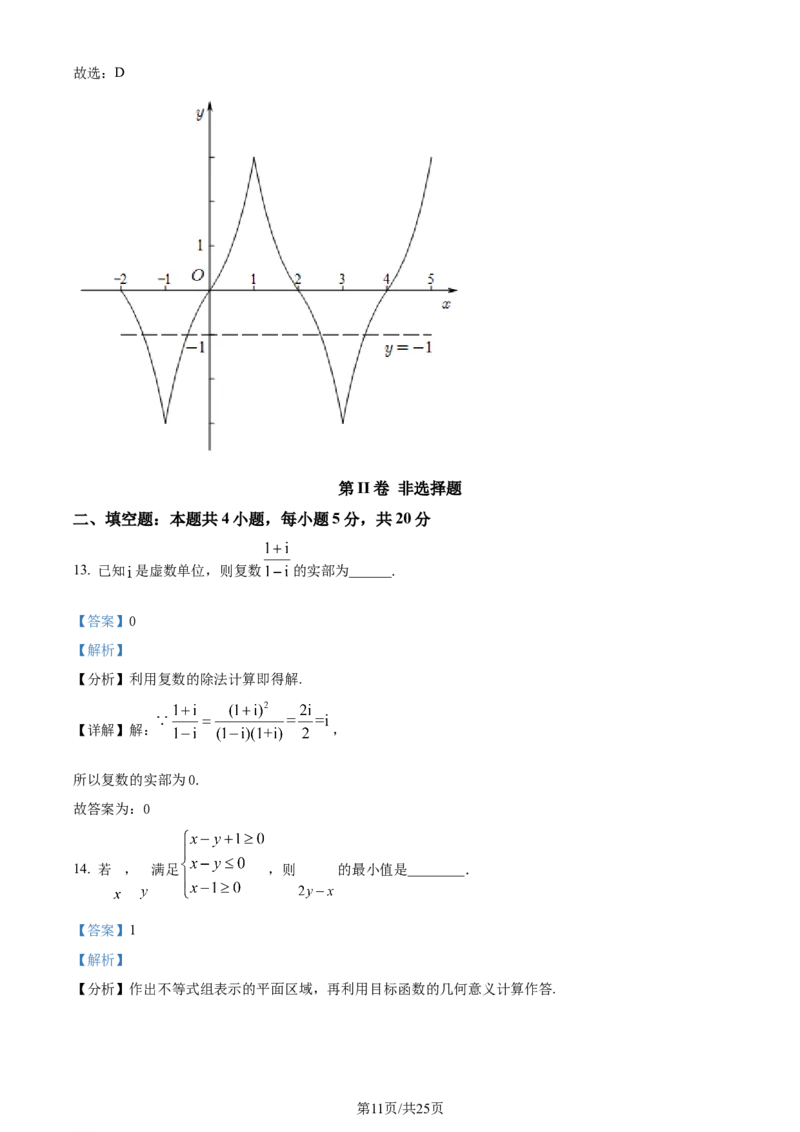
12. 定义在 上的奇函数 ,满足 ,当 时, , ,
则函数 在 的零点个数为( )
A. 7 B. 6 C. 5 D. 4
【答案】D
【解析】
【分析】根据已知条件求得 时, 的解析式,结合 的奇偶性和对称性画出 在区
间 的图象,由 来确定 的零点个数.
【详解】 是定义在 上的奇函数, ,
当 时, , ,
,
所以当 时, .
是奇函数,图象关于原点对称,
由于 ,所以 图象关于直线 对称,由此画出 在区间 的图象如下图所
示,
由图可知 有 个解,也即 有 个解,即 有 个零点.
第10页/共25页
学科网(北京)股份有限公司故选:D
第II卷 非选择题
二、填空题:本题共4小题,每小题5分,共20分
13. 已知 是虚数单位,则复数 的实部为______.
【答案】0
【解析】
【分析】利用复数的除法计算即得解.
【详解】解: ,
所以复数的实部为0.
故答案为:0
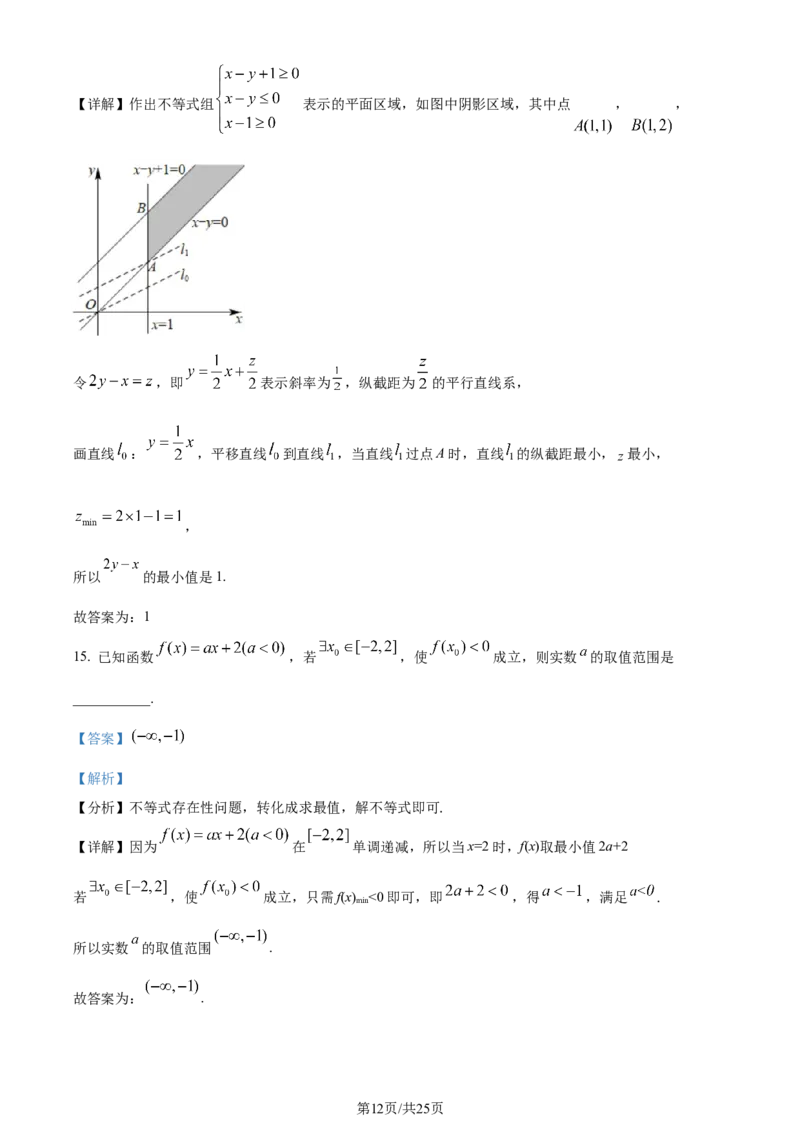
14. 若 , 满足 ,则 的最小值是________.
【答案】1
【解析】
【分析】作出不等式组表示的平面区域,再利用目标函数的几何意义计算作答.
第11页/共25页
学科网(北京)股份有限公司【详解】作出不等式组 表示的平面区域,如图中阴影区域,其中点 , ,
令 ,即 表示斜率为 ,纵截距为 的平行直线系,
画直线 : ,平移直线 到直线 ,当直线 过点A时,直线 的纵截距最小, 最小,
,
所以 的最小值是1.
故答案为:1
15. 已知函数 ,若 ,使 成立,则实数 的取值范围是
___________.
【答案】
【解析】
【分析】不等式存在性问题,转化成求最值,解不等式即可.
【详解】因为 在 单调递减,所以当x=2时,f(x)取最小值2a+2
若 ,使 成立,只需f(x) <0即可,即 ,得 ,满足 .
min
所以实数 的取值范围 .
故答案为: .
第12页/共25页
学科网(北京)股份有限公司【点睛】结论点睛:本题考查不等式的恒成立与有解问题,可按如下规则转化:
一般地,已知函数 ,
(1)若 , ,总有 成立,故 ;
(2)若 , ,有 成立,故 ;
(3)若 , ,有 成立,故 ;
(4)若 , ,有 ,则 的值域是 值域的子集 .
16. 关于函数 有如下四个结论:
①对任意 , 都有极值;
②曲线 的切线斜率不可能小于 ;
③对任意 ,曲线 都有两条切线与直线 平行;
④存在 ,使得曲线 只有一条切线与直线 平行.
其中所有正确结论的序号是______.
【答案】②④
【解析】
【分析】举反例否定①;求得导函数 的取值范围判断②;取特例否定③;取特例证明④.
【详解】对①:当 时, , 为增函数,无极值.所以①错误;
对②: ,所以②正确.
对③:当 时, ,
设切点 ,由 ,可得 或
第13页/共25页
学科网(北京)股份有限公司则切点为 或
则所求切线方程为 或
这两条切线中 与 平行, 与 重合.
即当 时,曲线 只有一条切线与直线 平行,且这条切线的切点的横坐标为 ,所以
③错误;
对④:由③可知,④正确.
故答案为:②④
三、解答题:共 70 分.解答应写出文字说明、证明过程或演算步骤.第 17~21 题为必考题,
每个试题考生都必须作答.第 22、23 题为选考题,考生根据要求作答.
(一)必考题:共 60 分.
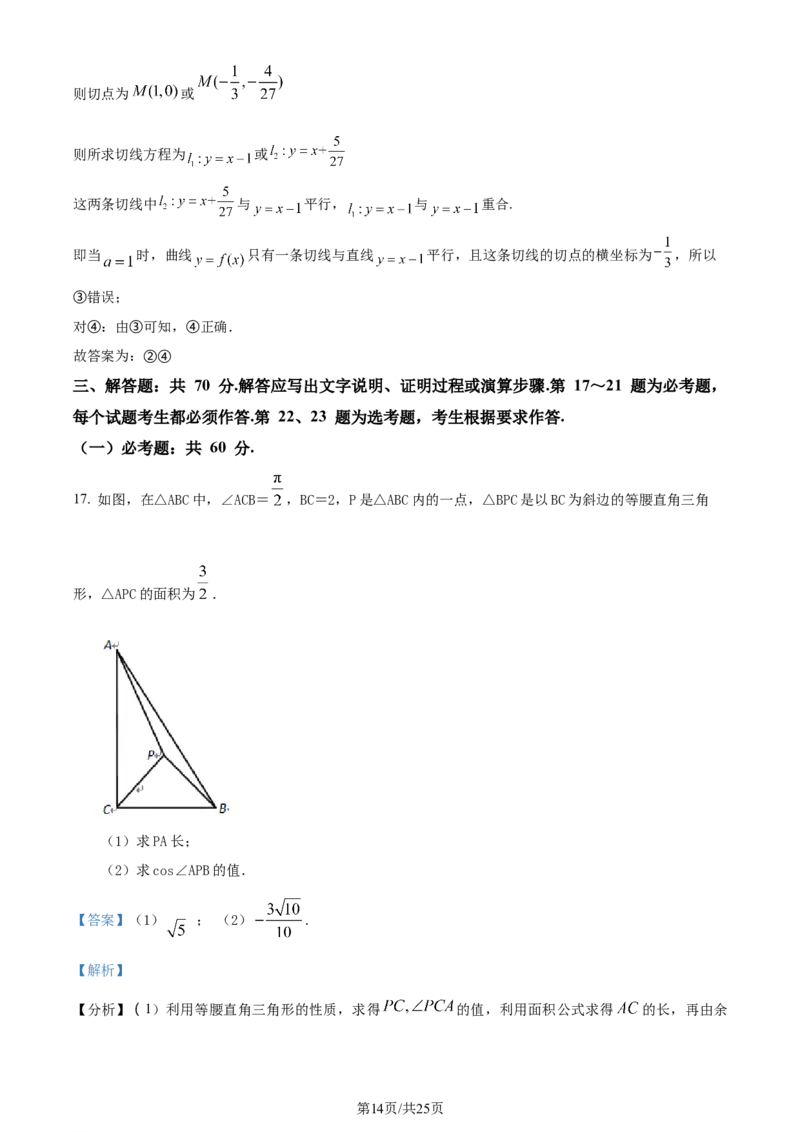
17. 如图,在△ABC中,∠ACB= ,BC=2,P是△ABC内的一点,△BPC是以BC为斜边的等腰直角三角
形,△APC的面积为 .
(1)求PA长;
(2)求cos∠APB的值.
【答案】(1) ; (2) .
【解析】
【分析】(1)利用等腰直角三角形的性质,求得 的值,利用面积公式求得 的长,再由余
第14页/共25页
学科网(北京)股份有限公司弦定理求得 的长;(2)在三角形 中,用正弦定理求得 的值,再利用诱导公式求得
的值.
【详解】(1)由题设∠PCA= ,PC= , AC·PC·sin = ,得AC=3.
(或由题设 AC· BC= ,得AC=3.)
在△PAC中,由余弦定理得PA= = .
(2)在△APC中,由正弦定理得 ,得sin∠APC= .
于是cos∠APB=cos( -∠APC)=-sin∠APC= .
【点睛】本小题主要考查解三角形,考查正弦定理和余弦定理的应用.题目的突破口在于三角形
为等腰直角三角形,根据等腰直角三角形的性质可得出角度和边长,再结合正弦定理和余弦定理适用的条
件,即可求得题目所求.属于中档题.
18. 已知函数 ,且 .
(1)当 时,求曲线 在点 处的切线方程;
(2)求函数 的单调区间;
(3)若函数 有最值,写出 的取值范围.(只需写出结论)
【答案】(1)
(2)答案见解析 (3)
【解析】
【分析】(1)求出函数的导函数,即可求出切线的斜率,即可求出切线方程;
(2)求出函数的导函数,分 和 两种情况讨论,讨论导函数的符号变换,进而得到函数的单调
区间;
第15页/共25页
学科网(北京)股份有限公司(3)由(2)中的结论判断即可.
【小问1详解】
解:当 时,由题设知 .
因为 ,
所以 .
所以 在 处的切线方程为 .
【小问2详解】
解:因为 ,所以 .
当 时,定义域为 .
且
故 的单调递减区间为 , , ,
当 时,定义域为 , 当 变化时, , 的变化情况如下表:
单调递减 极小值 单调递增 极大值 单调递减
故 的单调递减区间为 , ,单调递增区间为 .
综上所述,
当 时, 的单调递减区间为 , , ,
当 时,故 的单调递减区间为 , ,
第16页/共25页
学科网(北京)股份有限公司单调递增区间为 .
【小问3详解】
解:由(2)可知要使函数 有最值,则 ,
使得函数在 上单调递减,在 上单调递增,在 上单调递减,
且当 时 ,当 时 ,
所以 在 处取得极小值即最小值,在 处取得极大值即最大值.
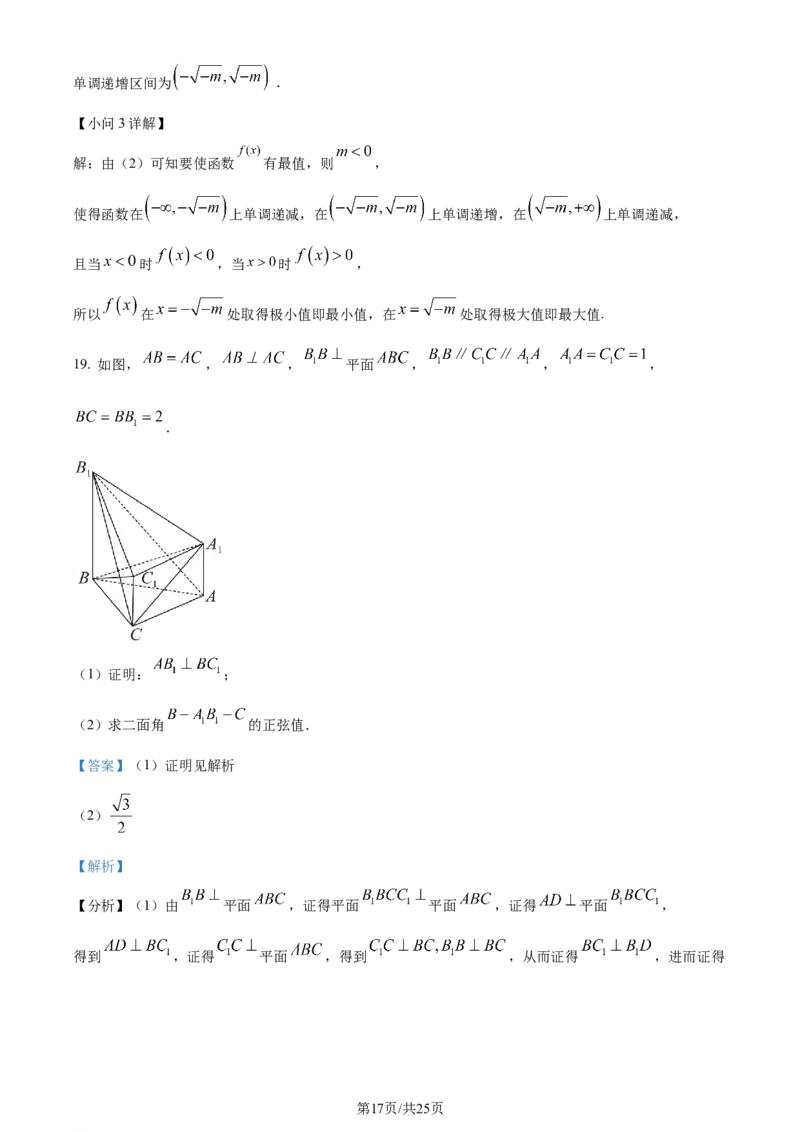
19. 如图, , , 平面 , , ,
.
(1)证明: ;
(2)求二面角 的正弦值.
【答案】(1)证明见解析
(2)
【解析】
【分析】(1)由 平面 ,证得平面 平面 ,证得 平面 ,
得到 ,证得 平面 ,得到 ,从而证得 ,进而证得
第17页/共25页
学科网(北京)股份有限公司平面 ,即可得到 .
(2)建立空间直角坐标系,利用向量法求出二面角即可.
【小问1详解】
取D为线段BC中点,连接AD与DB,
1
平面 , 平面 ,
平面 平面 ,
平面 平面 .
又 是以BC为斜边的等腰直角三角形,
, 平面 .
平面 ,
.
, 平面 ,
平面 ,
平面 ,
, ,
与 都为直角三角形,又 , .
第18页/共25页
学科网(北京)股份有限公司, , ,
, .
平面 , 平面 , ,
平面 , 平面 , .
【小问2详解】
, 平面 ,
, ,又 .
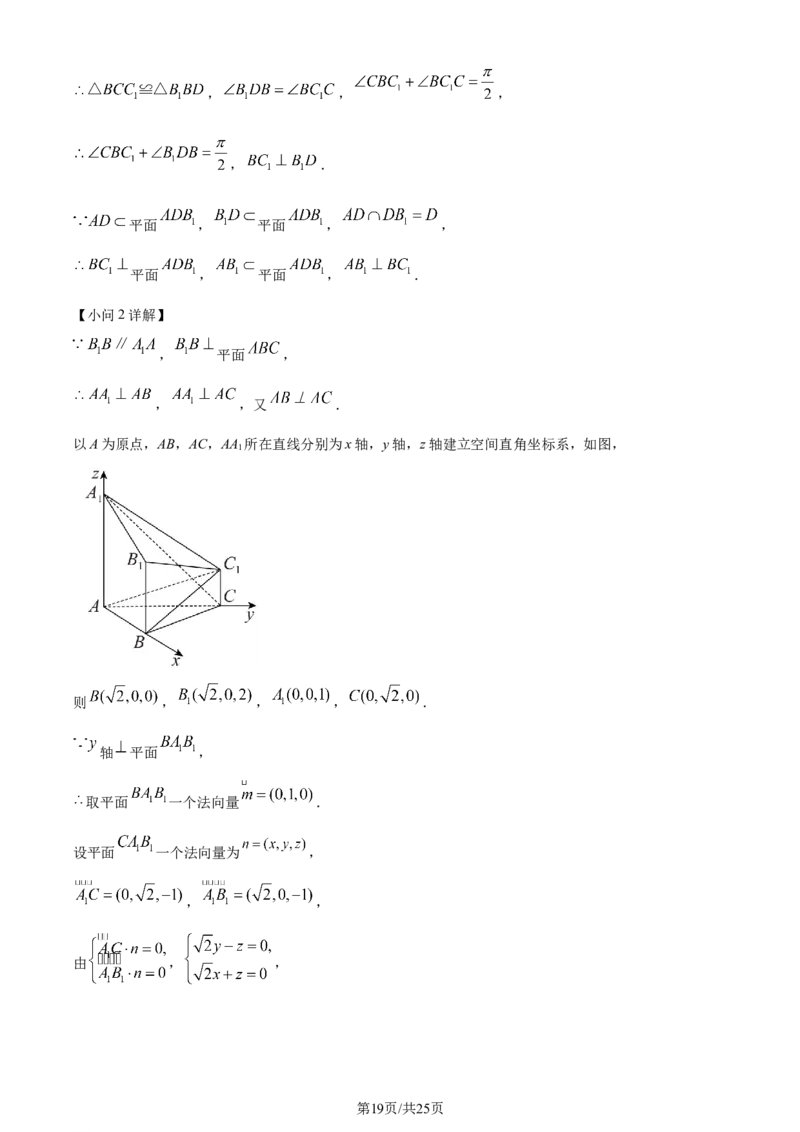
以A为原点,AB,AC,AA 所在直线分别为x轴,y轴,z轴建立空间直角坐标系,如图,
1
则 , , , .
轴 平面 ,
取平面 一个法向量 .
设平面 一个法向量为 ,
, ,
由 , ,
第19页/共25页
学科网(北京)股份有限公司可得 .
.
二面角 的正弦值为 .
20. 已知函数 ( )图象的相邻两条对称轴之间的距离为 .
(1)求 的单调递增区间以及 图象的对称中心坐标;
(2)是否存在锐角 , ,使 , 同时成立?若存在,求出
角 , 的值;若不存在,请说明理由.
【答案】(1)递增区间为 ( );对称中心 坐标为 (
的
)
(2)存在; ,
【解析】
【分析】(1)根据三角恒等变换化简解析式,再根据正弦型函数图象性质求解即可;
(2)由诱导公式可得 ,又 ,代入化简可得
, 。
【小问1详解】
解:
第20页/共25页
学科网(北京)股份有限公司,
由 图象的相邻两条对称轴之间的距离为 ,得 的最小正周期 ,解得 .
所以 ,
由 ( ),得 ( ),
所以 的递增区间为 ( ),
由 ( ),得 ( );
所以 图象的对称中心的坐标为 ( ).
【小问2详解】
解:存在.
因为 , ,
所以 ,
所以 .
又 , ,所以 ,
即 ,即 ,
即 ,即 ,
第21页/共25页
学科网(北京)股份有限公司所以 ,由 为锐角,得 ,所以 , ,从而 .
故存在 , 符合题意.
21. 已知函数 .
(1)若函数 有两个零点,求 的取值范围;
(2)若 , ,求 的取值范围.
【答案】(1)
(2)
【解析】
【分析】(1)先求导,再对参数进行分类讨论,根据零点存在定理即可求解.
(2) 先求导,再对参数进行分类讨论,根据单调性即可求解
【小问1详解】
解:由 ,得 ,
若 ,则 , 单调递增, 不 可能有两个零点,不符合题意;
若 ,令 ,得 ,则 时, , 单调减;
则 时, , 单调增,则 在 时取得极小值 ,也即为最小值,
又 时, ; 时, ,函数 有两个零点,则有 ,
即 ,解得 .
所以, 有两个零点时, 的取值范围是 .
【小问2详解】
解:不等式 ,即 ,
第22页/共25页
学科网(北京)股份有限公司则 , , .
①当 时, ,令 ,则 ,由 ,则
,故 即 在 时单调递增,则 ,
所以 在 时单调递增,故 ,所以 成立.
②当 时, , ,
则 ,使得 ,由上可知 在 时单调递增,
则当 时, ,则 单调递减,所以 ,不满足条件.
综上所述, 的取值范围是 .
(二)选考题:共 10 分.请考生在第 22、23 题中任选一题作答.如果多做,则按所做的第一
题计分.
[选修 4-4:坐标系与参数方程](10分)
22. 在平面直角坐标系中,曲线 的参数方程为 ( 为参数).以原点 为极点, 轴的非负
半轴为极轴建立极坐标系,直线 的极坐标为
(1)求曲线 的普通方程与直线 的直角坐标方程;
(2)设直线 与曲线 交于 两点,点 的坐标为 ,证明:直线 关于 轴对称.
【答案】(1) ; ;(2)证明见解析.
【解析】
【分析】(1)利用同角的三角函数关系式把曲线 的参数方程化成普通方程,利用直角坐标方程与极坐
标方程互化公式,结合两角和的余弦公式把直线 的极坐标方程,化成直角坐标方程;
第23页/共25页
学科网(北京)股份有限公司(2)通过解方程组求出 两点坐标,根据直线斜率公式进行证明即可.
【详解】(1)由曲线 参数方程 ( 为参数)可得
的
曲线 的普通方程为 .
直线 的极坐标方程可变形为:
,
是
于 ,其直角坐标方程为 .
(2)由方程组 消元,有 .
由此可知,点 的坐标分别为
直线 的斜率分别为
所以,
于是,直线 关于 轴对称.
[选修 4-5:不等式选讲](10 分)
23. 已知函数
(1)求不等式 的解集;
(2)记函数 的最小值为 ,若 是正实数,且 ,求证 .
【答案】(1)不等式的解集为 ,(2)证明见详解
第24页/共25页
学科网(北京)股份有限公司【解析】
【分析】
(1)分3种情况解出即可
(2)首先求出 ,即可得到 ,然后
,用基本不等式即可证明.
【详解】(1) 等价于
或 或
解得 或 或
所以不等式的解集为
(2)因为
当 时等号成立,所以 的最小值为3,即
所以
所以
当且仅当 时等号成立
【点睛】本题考查的是含绝对值不等式的解法及利用基本不等式求最值,属于典型题.
第25页/共25页
学科网(北京)股份有限公司