文档内容
焦作市博爱一中 2023—2024 学年(上)高三年级期中考试
数学
考生注意:
1.答题前,考生务必用黑色签字笔将自己的姓名、准考证号、座位号在答题卡上填写清楚;
2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,在试卷上作答无效;
3.考试结束后,请将本试卷和答题卡一并交回.
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有
一项是符合题目要求的.
1. 已知函数 ,若f(x)在R上是增函数,则实数a的取值范围是( )
A. ( ,1] B. [ , ] C. ( ,+∞) D. [1,2]
2. 已知 , , ,则 的大小关系为
A. B.
C. D.
3. 已知函数 在区间 单调递增,直线 和 为函数 的图象的
两条对称轴,则 ( )
A. B. C. D.
4. 赵爽弦图是中国古代数学的重要发现,它是由四个全等直角三角形与一个小正方形拼成的一个大正方形
(如图).已知小正方形的面积为1,直角三角形中较小的锐角为 ,且 ,则大正方形的面积为
( )
第1页/共6页
学科网(北京)股份有限公司A. 4 B. 5 C. 16 D. 25
5. 若直线 : 经过第四象限,则 的取值范围为( )
A. B.
.
C D.
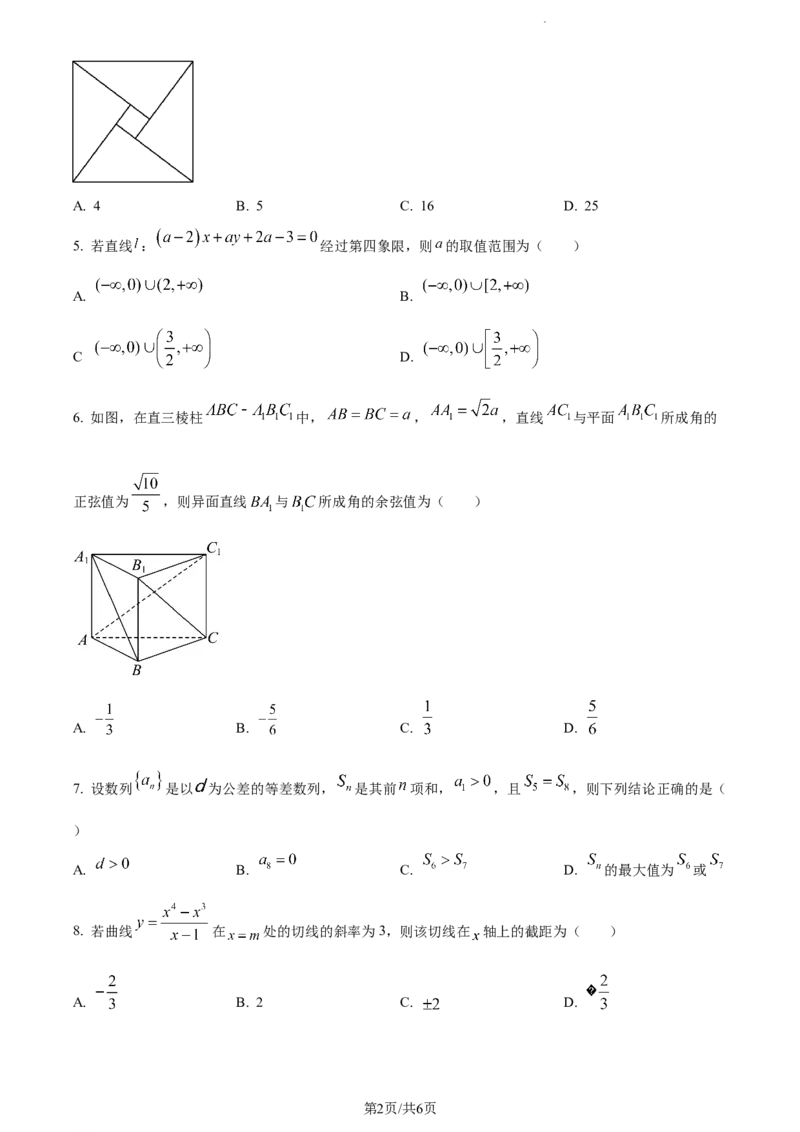
6. 如图,在直三棱柱 中, , ,直线 与平面 所成角的
正弦值为 ,则异面直线 与 所成角的余弦值为( )
A. B. C. D.
7. 设数列 是以 为公差的等差数列, 是其前 项和, ,且 ,则下列结论正确的是(
)
A. B. C. D. 的最大值为 或
8. 若曲线 在 处的切线的斜率为3,则该切线在 轴上的截距为( )
A. B. 2 C. D.
第2页/共6页
学科网(北京)股份有限公司二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符
合题目要求.全部选对的得5分,有选错的得0分,部分选对的得2分.
9. 下列各组函数中是同一个函数的是( )
A. 与
B. 与
C. 与
D. 与
10. 若 , ,且 ,则( )
A. B.
C. D.
11. 已知函数 ,则下列说法正确 的是( )
A. 的最小正周期为
B. 在 上单调递减
C.
D. 的定义域为
12. 已知复数 , , , 为坐标原点, , ,
第3页/共6页
学科网(北京)股份有限公司对应的向量分别为 , , ,则以下结论正确的有( )
A.
B. 若 ,则
C. 若 ,则 与 的夹角为
D. 若 ,则 为正三角形
三、填空题:本大题共4个小题,每小题5分,共20分.
13. 设样本数据 , , , 的平均数为 ,方差为 ,若数据 , , ,
的平均数比方差大4,则 的最大值是_____________.
14. 某同学画“切面圆柱体”(用与圆柱底面不平行的平面切圆柱,底面与切面之间的部分叫做切面圆柱
体),发现切面与圆柱侧面的交线是一椭圆(如图所示).若该同学所画的椭圆的离心率为 ,则“切
面”所在平面与底面所成锐二面角的大小为__________.
15. 是空间的一个基底,向量 , 是空间的另一个基底,向量
,则 __________.
16. 各项均为正数的等比数列 的前 项和为 ,若 , ,则 的最小值为
______.
四、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
第4页/共6页
学科网(北京)股份有限公司17. 在锐角 ABC中,角A,B,C对边分别 为a,b,c,设向量 , ,且 .
△
(1)求证:
(2)求 的取值范围.
18. 某蔬果经销商销售某种蔬果,售价为每千克25元,成本为每千克15元,其销售宗旨是当天进货当天
销售,若当天未销售完,未售出的全部降价以每千克10元处理完.据以往销售情况,按
进行分组,得到如图所示的频率分布直方图.
的
(1)根据频率分布直方图求该蔬果日需求量 平均数 (同组数据用区间中点值代表);
(2)该经销商某天购进了250千克蔬果,假设当天的日需求量为 千克( ),利润为 元.
①求 关于 的函数表达式;
②根据频率分布直方图估计利润 不小于1750元的概率.
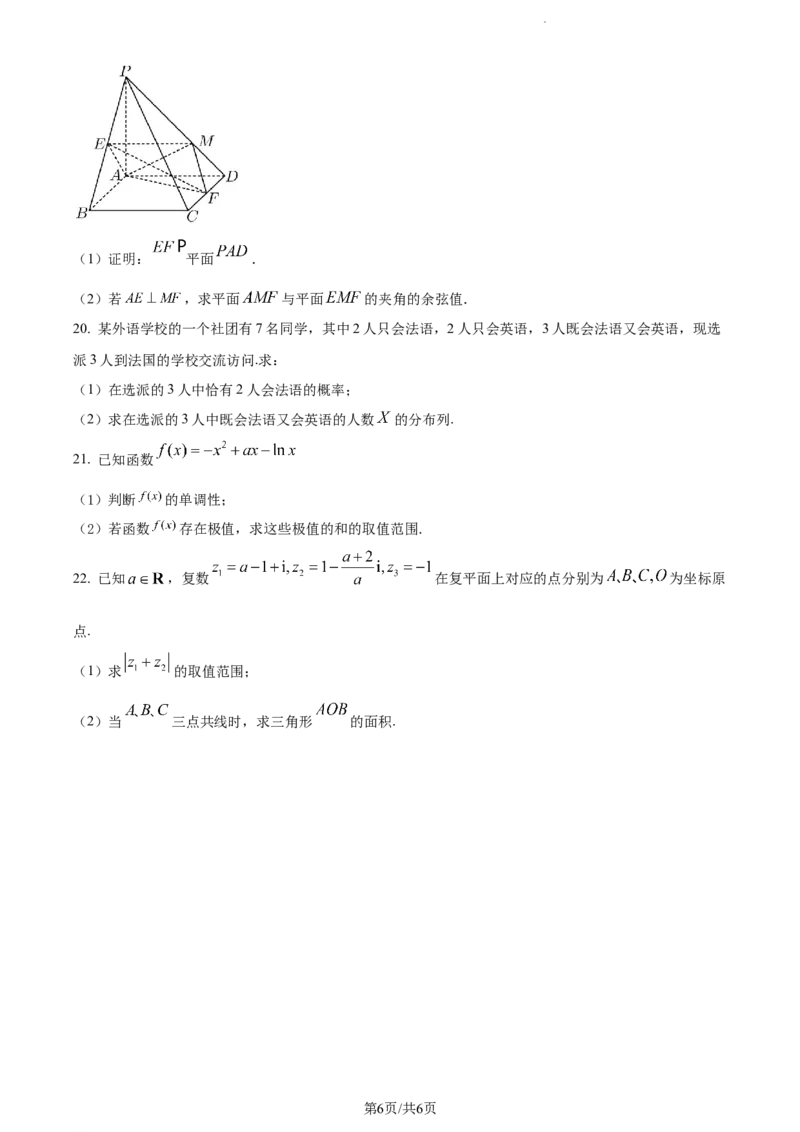
19. 如图,在四棱锥 中, 底面 ,底面 为正方形, , , 分别
的
是 , 中点, 是 上一点.
第5页/共6页
学科网(北京)股份有限公司(1)证明: 平面 .
(2)若 ,求平面 与平面 的夹角的余弦值.
20. 某外语学校的一个社团有7名同学,其中2人只会法语,2人只会英语,3人既会法语又会英语,现选
派3人到法国的学校交流访问.求:
(1)在选派的3人中恰有2人会法语的概率;
(2)求在选派的3人中既会法语又会英语的人数 的分布列.
21. 已知函数
(1)判断 的单调性;
(2)若函数 存在极值,求这些极值的和的取值范围.
22. 已知 ,复数 在复平面上对应的点分别为 为坐标原
点.
(1)求 的取值范围;
(2)当 三点共线时,求三角形 的面积.
第6页/共6页
学科网(北京)股份有限公司