文档内容
2025-2026 学年度第一学期赣州市十三校期中联考
高二年级数学试卷
一、选择题(本大题共8小题,每小题5分,共40分,每小题只有一项符合题目要求)
1.直线 的倾斜角是( )
A. B. C. D.0
2.已知圆 与圆 ,则两圆的位置关系是( )
A.内含 B.外切 C.相交 D.外离
3.已知直线 与直线 平行,则实数 的值为( )
A.-1 B.2 C.-1或2 D.1或-2
4.已知点 ,在 轴上求一点 ,使 最小,则点 的坐标为( )
A. B. C. D.
5.已知 是椭圆 的左、右焦点,经过 的直线与椭圆相交于 两点,
若 ,则椭圆的离心率为( )
A. B. C. D.
6.已知 为抛物线 的焦点, 的三个顶点都在 上,且 为 的重心.
若 的最大值为10,则 ( )
A.1 B.2 C.3 D.4
7.已知正方形 的边长为2,现将 沿对角线 翻折,得到三棱锥 .记AC、BC、
AD的中点分别为O、M、N,则下列结论错误的是( )
A.AC上平面BOD
B.三棱锥D-ABC体积的最大值为
C.三棱锥D-ABC的外接球的表面积为定值
D.MN与平面BOD所成角的范围是
8.在天文观测中,天文学家利用圆锥曲线的光学性质分析星系光线传播.如图,从双曲线右焦点 发出
的模拟星系光线,经双曲线模型镜面反射后形成发散光线,且反射光线的反向延长线经过左焦点 .已知双曲线的方程为 ,当入射光线 和反射光线 ( 为入射点)互相垂直时,求 的
大小( )
A. B. C. D.
二、多选题(本大题共3小题,每小题6分,共18分,全部选对得6分,部分选对的得部分
分,有选错的得0分)
9.已知抛物线 与抛物线 关于 轴对称,则下列说法正确的是( )
A.抛物线 的焦点坐标是
B.抛物线 关于 轴对称
C.抛物线 的准线方程为
D.抛物线 的焦点到准线的距离为4
10.已知直线 与圆 ,则下列说法正确( )
A.直线 恒过定点
B.当直线 与圆 相切时,切线方程是
C.当 时,圆 上恰有三个点到直线 的距离等于
D.圆 上的一点 到直线 的最大距离是
11.已知椭圆 ,我们把圆 称为 的蒙日圆, 为原点,点
在 上,延长 与 的蒙日圆交于点 ,则( )
A. 的最大值为
B.若 为 的中点,则 的离心率的最小值为
C.过点 不可能作两条互相垂直的直线都与 相切
D.若点 在 上,则 的蒙日圆面积最小为
三、填空题(本大题共3小题,每小题5分,共15分)
12.若圆锥的高为10,底面圆的半径为2,则这个圆锥的体积为___________.13.已知点 到点 的距离比到 轴的距离大3,则点 的轨迹方程为___________.
14.已知双曲线 的左焦点为 ,右焦点为 ,过 作圆
的切线,切点为 ,切线 交双曲线右支于点 ,且 为坐标原点,
则双曲线的离心率为__________.
四、解答题(本大题共5小题,共77分,解答须写出文字说明、证明过程和演算步骤)
15.已知在平面直角坐标系中,圆 经过点 和 ,且圆心 在直线 上,直线
.
(1)求圆 的标准方程;
(2)若直线 被圆 截得的弦长为 ,求实数 的值.
16.已知抛物线 的焦点为 ,焦点 到准线的距离为5.
(1)求抛物线 的标准方程及焦点 的坐标;
(2)过焦点 作斜率为 2 的直线 ,交抛物线 于 ,两点,若点 在抛物线 上,求
的面积.
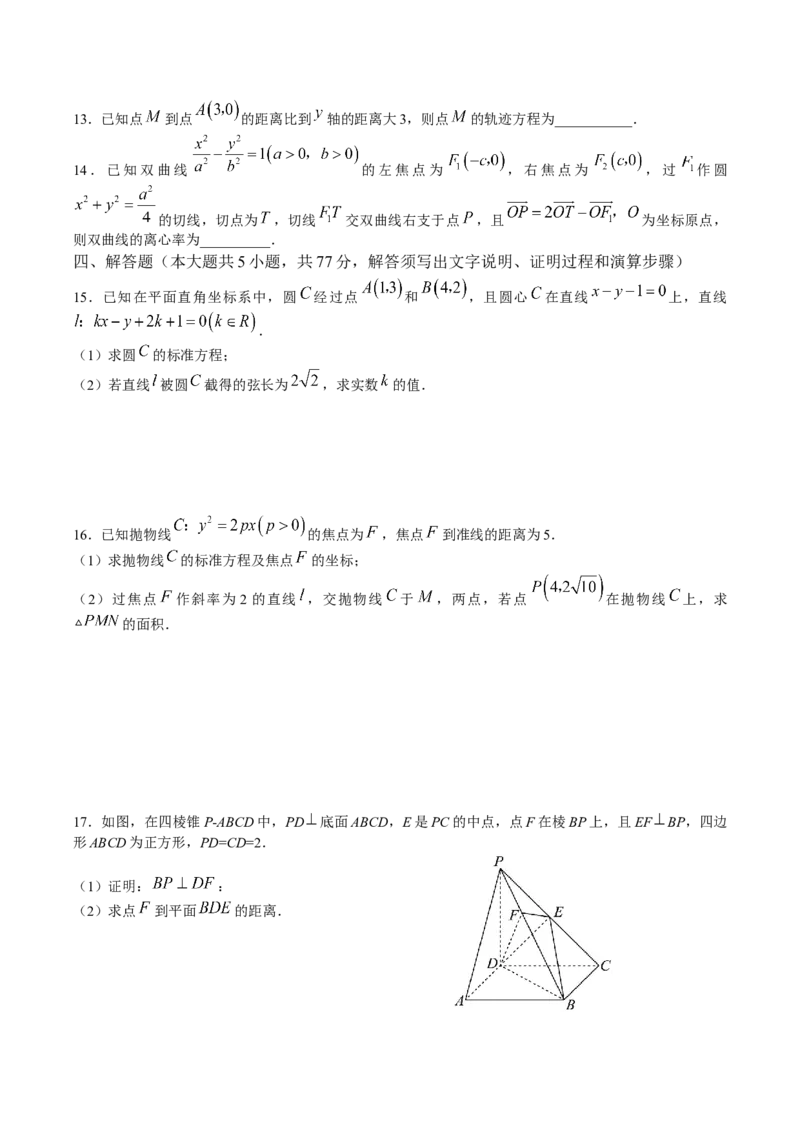
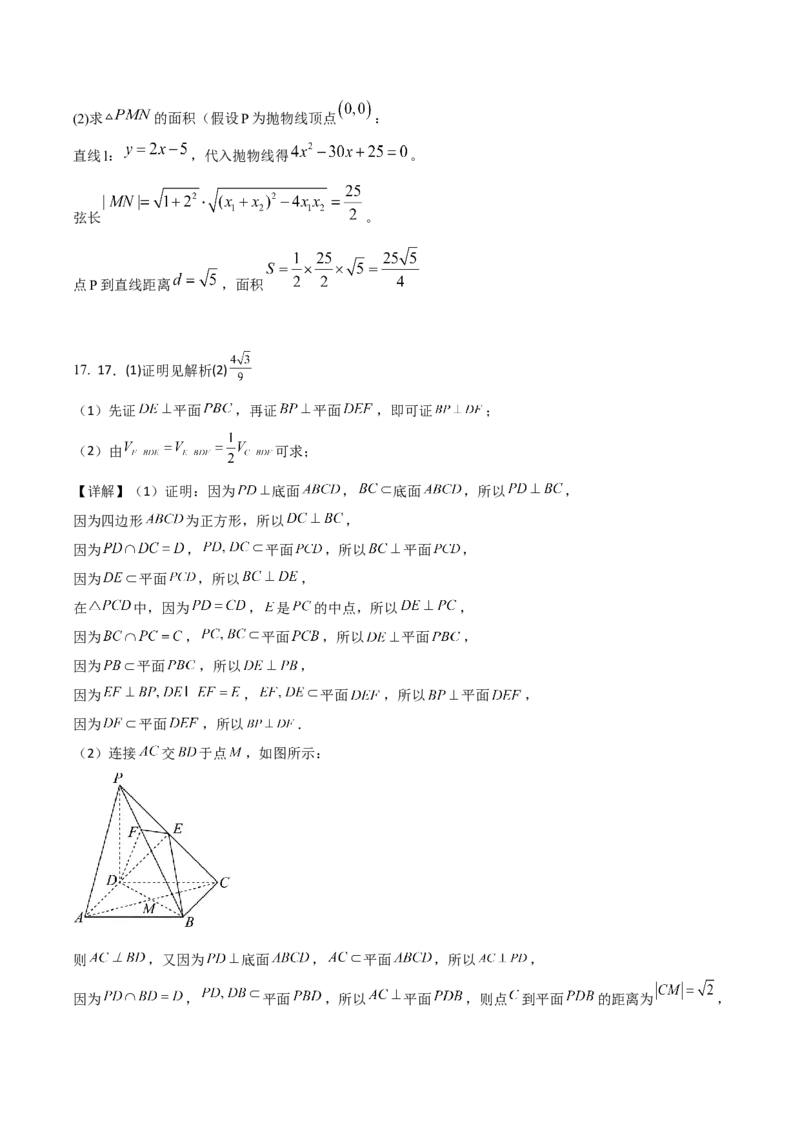
17.如图,在四棱锥P-ABCD中,PD 底面ABCD,E是PC的中点,点F在棱BP上,且EF BP,四边
形ABCD为正方形,PD=CD=2.
(1)证明: :
(2)求点 到平面 的距离.18.已知椭圆 分别是左、右焦点, 是椭圆 上点, 的最大值为
3,当 为椭圆上顶点时, 为等边三角形.
(1)求椭圆 的标准方程;
(2)设 、 分别是椭圆 的左、右顶点,若直线 与 交于点 、 ,且 .证明:直线
过定点.
19.已知动点 与定点 的距离和 到定直线 的距离的比为常数 .其中 ,
且 ,记点 的轨迹为曲线 .
(1)求C的方程,并说明轨迹的形状;
(2)设点 ,若曲线 上两动点 均在 轴上方, ,且 与 相交于点 .
①当 时,求证: 的值及 的周长均为定值;
②当 时,记 的面积为 ,其内切圆半径为 ,试探究是否存在常数 ,使得 恒成立?
若存在,求 (用 表示);若不存在,请说明理由.题号 1 2 3 4 5 6 7 8 9 10
答案 B C A A C D D B AC ABD
题号 11
答案 ABD
1.答案:B
直线倾斜角与斜率的关系
解析:直线方程化为斜截式: ,斜率 。
倾斜角 满足 ,且 。
因 ,故倾斜角为 。
2. 答案:C(相交)
两圆位置关系的判断(圆心距与半径的关系)
解析:求圆心与半径:圆 圆心 、半径 ;圆 圆心 、半径 。
计算圆心距: 。
判断位置: 因 ,故两圆相交。
3. 答案:A(-1)
两直线平行的充要条件 且
解析:化简直线:直线 : 化为 ;直线 。
列平行条件: (斜率相等),且 (截距不等)。
求解验证:解得 (代入满足截距不等), 不满足斜率相等,故答案为 - 1。
4. 答案:A
轴对称求最短路径(两点之间线段最短)
解析:找对称点:作 关于 x 轴的对称点 。
求直线方程:直线 的斜率 ,方程为 。
求交点 P:令 ,解得 ,故 。
5. 答案:C
椭圆定义与直角三角形性质解析:判断三角形形状: ,满足 ,故 。
用椭圆定义求a: , ,两式相加得 。
求a与c:因 ,故 , ; ,在 中,
, 。计算离心率: 。
6. 答案:D
抛物线定义与重心性质
解析:抛物线基本量:焦点 ,准线 ,由定义得 , 。
重心性质:设 , , ,重心纵坐标 ,故 。
求最大值: ,当 (抛物线最低点)时,最大值为 。
解方程: ,得 。
7.D
【详解】对于A中,因为 为正方形,可得 ,
又由 ,且 平面 ,所以 平面 ,所以A正确;
对于B中,当平面 平面 时,此时 到平面 的距离最大,
即三棱锥 高的最大值为 ,
此时三棱锥 的最大体积为 ,所以B正确;
对于C中,由 ,所以三棱锥 外接球的球心为 ,
即外接球的半径 ,所以三棱锥 外接球的表面积为 (定值),
所以C正确;
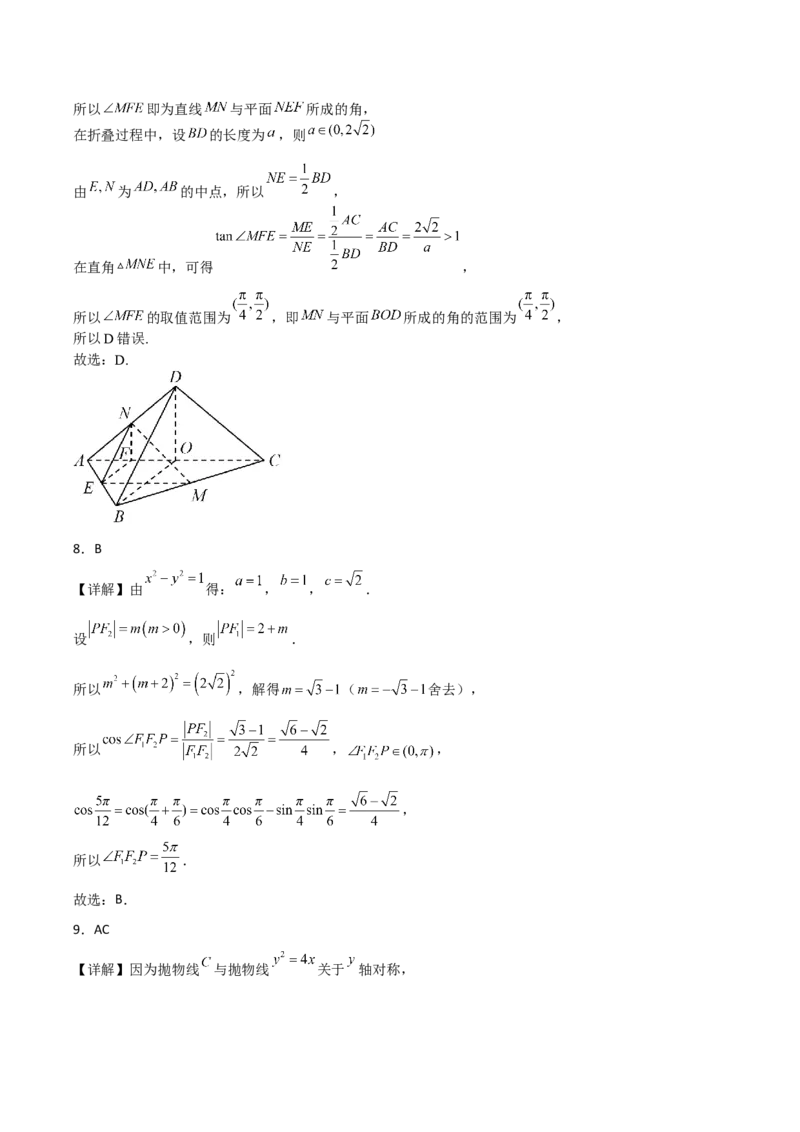
对于D中,如图所示,取 的中点 ,分别连接 ,
因为 分别为 中点,可得 且 ,
所以平面 平面 ,
又因为 平面 ,所以 平面 ,
因为 ,所以 平面 ,所以 即为直线 与平面 所成的角,
在折叠过程中,设 的长度为 ,则
由 为 的中点,所以 ,
在直角 中,可得 ,
所以 的取值范围为 ,即 与平面 所成的角的范围为 ,
所以D错误.
故选:D.
8.B
【详解】由 得: , , .
设 ,则 .
所以 ,解得 ( 舍去),
所以 , ,
,
所以 .
故选:B.
9.AC
【详解】因为抛物线 与抛物线 关于 轴对称,所以抛物线 的方程为 ,
则抛物线 的焦点坐标是 ,准线方程为 ,故A、C正确;
抛物线 关于 轴对称,故B错误;
抛物线 的焦点到准线的距离为 ,故D错误.
故选:AC
10.ABD
【详解】对于A,将直线 转化为 ,
由 ,解得 ,直线 恒过定点 ,A正确;
对于B,圆 ,可得圆心 ,半径 ,
由直线 与圆相切,可得圆心C到直线l的距离 ,
即 ,解得 ,
故切线方程为 ,即 ,B正确;
对于C,当 时,直线 ,
点 到此直线距离为 ,
因此圆 上恰有四个点到直线 的距离等于 ,C错误;
对于D,因为直线恒过定点 ,可得 ,
当 时,圆心C到直线l的距离最大,且最大值为 ,
所以圆上的点到直线的最大距离为 ,D正确.
故选:ABD.11.ABD
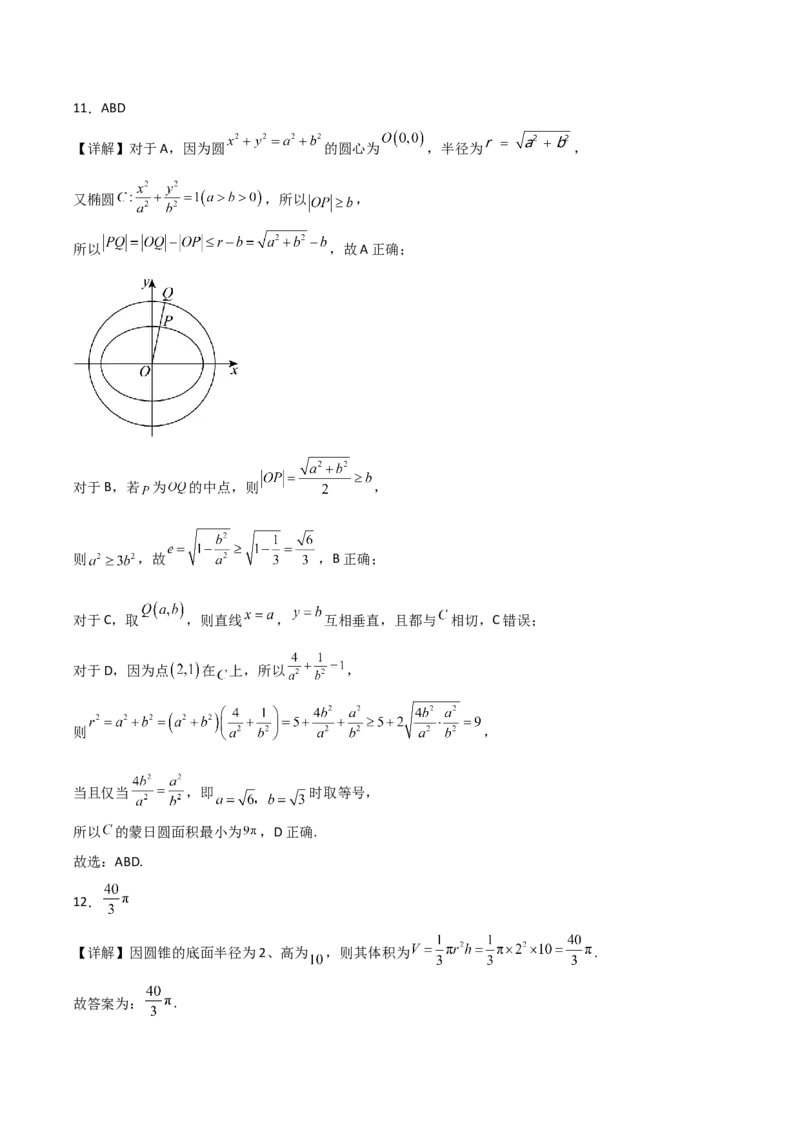
【详解】对于A,因为圆 的圆心为 ,半径为 ,
又椭圆 ,所以 ,
所以 ,故A正确;
对于B,若 为 的中点,则 ,
则 ,故 ,B正确;
对于C,取 ,则直线 , 互相垂直,且都与 相切,C错误;
对于D,因为点 在 上,所以 ,
则 ,
当且仅当 ,即 时取等号,
所以 的蒙日圆面积最小为 ,D正确.
故选:ABD.
12.
【详解】因圆锥的底面半径为2、高为 ,则其体积为 .
故答案为: .13. 答案: 或
解析:设 ,列条件: 。
分类讨论:
当 :平方化简得 ;
当 :平方化简得 。
14. 答案:
双曲线性质、向量运算、圆的切线性质
解析:切线性质: , , ,得T点坐标 。
向量运算: ,得 , 。
代入双曲线:化简得 ,解得 (舍)或 ,故
15. (12 分)
圆的标准方程、直线与圆的弦长公式
解析:求圆 C 的标准方程:
(1) 设 圆 心 ( 在 直 线 上 ) , 由 得
。
解得 ,圆心 ,半径 ,圆方程为 。
(2)求实数k的值:弦长 ,圆心到直线距离 。
直线 , ,解得 。
16. 抛物线的标准方程、直线与抛物线的位置关系
解析:求抛物线方程与焦点:
(1)焦点到准线距离 ,方程 ,焦点 。(2)求 的面积(假设P为抛物线顶点 :
直线l: ,代入抛物线得 。
弦长 。
点P到直线距离 ,面积
17. 17.(1)证明见解析(2)
(1)先证 平面 ,再证 平面 ,即可证 ;
(2)由 可求;
【详解】(1)证明:因为 底面 , 底面 ,所以 ,
因为四边形 为正方形,所以 ,
因为 , 平面 ,所以 平面 ,
因为 平面 ,所以 ,
在 中,因为 , 是 的中点,所以 ,
因为 , 平面 ,所以 平面 ,
因为 平面 ,所以 ,
因为 , 平面 ,所以 平面 ,
因为 平面 ,所以 .
(2)连接 交 于点 ,如图所示:
则 ,又因为 底面 , 平面 ,所以 ,
因为 , 平面 ,所以 平面 ,则点 到平面 的距离为 ,因为 是 的中点,所以 ,
因为底面正方形 边长为 ,所以 , ,
所以 , ,
所以 ,
,所以 .
在 中 ,满足 ,有 ,
所以 ,
设点 到平面 的距离为 ,
由 可得
18. (1)椭圆 的标准方程为
(2)( )证明见解析;( ) 面积的最大值为
【详解】(1)根据题意作图如下:
由题意得 ,所以 ,
因为 ,所以椭圆 的标准方程为 .
(2)( )证明:法一:由(1)可知 ,
设直线 的斜率为 ,则直线 的斜率为 ,设 ,
则直线 的方程为 ,直线 的方程为 ,
联立 ,化简得 ,因为 ,所以 ,即 ,
联立 ,化简得 ,
因为 ,所以 ,即 ,
则 ,
所以直线 的方程为 ,整理得 ,
所以直线 过定点 ,即右焦点 .
法二:设 ,又由(1)知 ,
所以 ,
则有 ,
又 ,则 ,代入上式可得 .
又因为 ,所以 .
设直线 的方程为 ,
联立 ,得 ,所以 ,且
所以 ,
由 ,
化简得 且 ,
即 ,解得 或 (舍),
所以直线 过定点 ,即右焦点 ;
19.(1)答案见解析
(2)① 证明见解析;②存在;
【详解】(1)设点 ,由题意可知 ,
即 ,
经化简,得 的方程为 ,
当 时,曲线 是焦点在 轴上的椭圆;
当 时,曲线 是焦点在 轴上的双曲线.
(2)设点 ,其中 且 ,
(ⅰ)由(1)可知 的方程为 ,
因为 ,所以 ,因此, 三点共线,且 ,
(法一)设直线 的方程为 ,联立 的方程,得 ,
则 ,
由(1)可知 ,
所以
,
所以 为定值1;
(法二)设 ,则有 ,解得 ,
同理由 ,解得 ,
所以 ,
所以 为定值1;
由椭圆定义 ,得 ,
,解得 ,同理可得 ,
所以
.
因为 ,所以 的周长为定值 .
(ⅱ)当 时,曲线 的方程为 ,轨迹为双曲线,
根据(ⅰ)的证明,同理可得 三点共线,且 ,
(法一)设直线 的方程为 ,联立 的方程,
得 ,
,(*)
因为 ,
所以,
将(*)代入上式,化简得 ,
(法二)设 ,依条件有 ,解得 ,
同理由 ,解得 ,
所以 .
由双曲线的定义 ,得 ,
根据 ,解得 ,
同理根据 ,解得 ,
所以
,由内切圆性质可知, ,
当 时, (常数).
因此,存在常数 使得 恒成立,且 .