文档内容
民乐一中 2023-2024 学年第一学期高三年级第二次诊断考试
数 学
一、选择题
1. 设全集 ,集合 , ,则 ( )
A. B. C. D.
【答案】D
【解析】
【分析】利用集合间的基本运算,即可得到答案;
【详解】因为 ,所以 ,
所以 .
故选:D.
2. 一元二次方程 ,( )有一个正根和一个负根的充分而不必要条件是( )
A. B. C. D.
【答案】C
【解析】
【分析】先由方程根的情况可得 ,求出 的范围,再根据充分条件和必要条件的定义即可得解.
【详解】因为一元二次方程 ,( )有一个正根和一个负根,
所以 ,解得 ,
所以一元二次方程 ,( )有一个正根和一个负根的充分而不必要条件可以是 .
故选:C.
第1页/共22页
学科网(北京)股份有限公司3. 已知点 是角 终边上一点,则 ( )
A. B. C. D.
【答案】D
【解析】
【分析】先求出点P到原点的距离,再根据正弦函数的定义求解.
【详解】依题意点P的坐标为 , , ;
故选:D.
4. 设 是等差数列 的前 项和,若 ,则 ( )
A. B. C. D.
【答案】A
【解析】
【分析】由等差数列的性质可知 、 、 、 成等差数列,根据题意可将 都用
表示,可求得结果.
【详解】由等差数列的性质可知 、 、 、 成等差数列,
∵ ,即 , ,
∴ , ,∴ , ,
∴ .
故选:A.
第2页/共22页
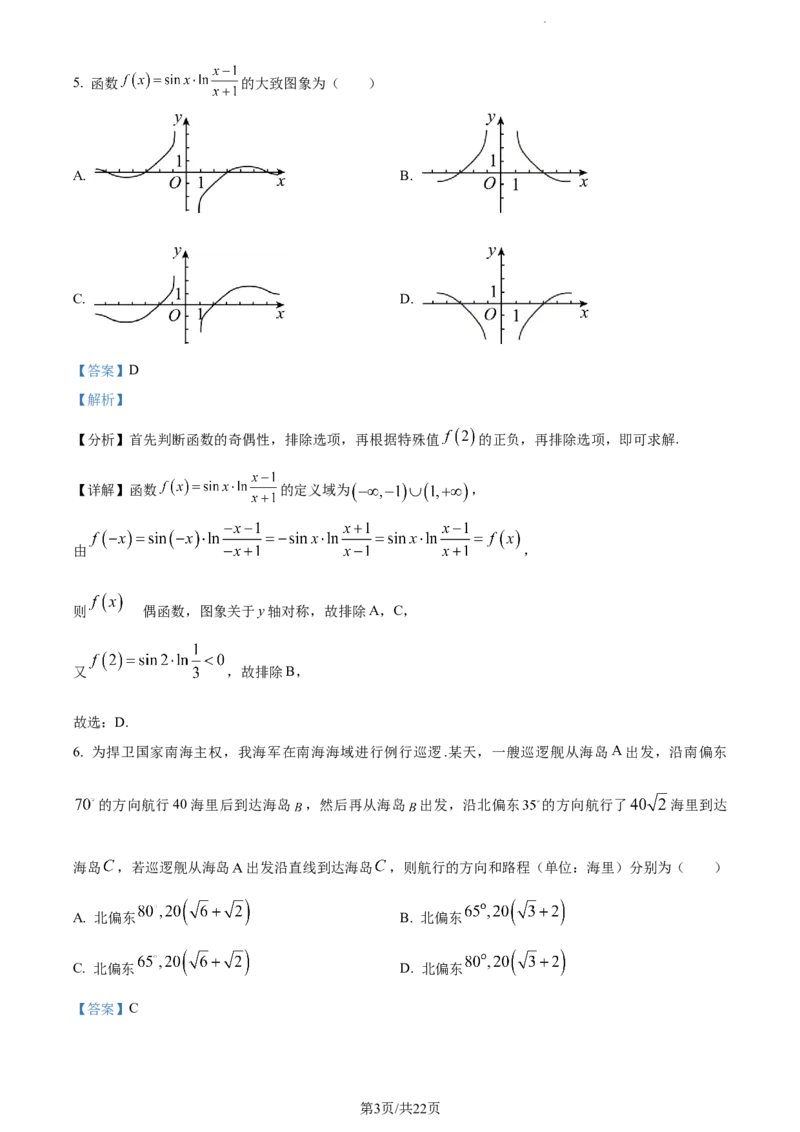
学科网(北京)股份有限公司5. 函数 的大致图象为( )
A. B.
C. D.
【答案】D
【解析】
【分析】首先判断函数的奇偶性,排除选项,再根据特殊值 的正负,再排除选项,即可求解.
【详解】函数 的定义域为 ,
由 ,
则 为偶函数,图象关于y轴对称,故排除A,C,
又 ,故排除B,
故选:D.
6. 为捍卫国家南海主权,我海军在南海海域进行例行巡逻.某天,一艘巡逻舰从海岛 出发,沿南偏东
的方向航行40海里后到达海岛 ,然后再从海岛 出发,沿北偏东 的方向航行了 海里到达
海岛 ,若巡逻舰从海岛 出发沿直线到达海岛 ,则航行的方向和路程(单位:海里)分别为( )
A. 北偏东 B. 北偏东
C. 北偏东 D. 北偏东
【答案】C
第3页/共22页
学科网(北京)股份有限公司【解析】
【分析】根据方位角的概念结合正弦定理、余弦定理求解.
【详解】作出示意图如图所示,
根据题意, ,
根据余弦定理,
因为 ,
所以
,
因为 ,所以
,
因为 为锐角,所以 ,
所以从海岛 出发沿直线到达海岛 ,航行的方向是北偏东 ,
航行的距离是 海里,
第4页/共22页
学科网(北京)股份有限公司.
故选:C
7. 设等差数列 , 的前n项和分别为 , ,若 ,则 为( )
A. 3 B. 4 C. 5 D. 6
【答案】C
【解析】
【分析】
根据等差数列的性质,得 ,此由可得结论.
【详解】 是等差数列,则 ,
∴ .
故选:C.
8. 设 ,则( )
A. B. C. D.
【答案】C
【解析】
【分析】构造函数 , 导数判断其单调性,由此确定 的大小.
【详解】方法一:构造法
设 ,因为 ,
当 时, ,当 时 ,
所以函数 在 单调递减,在 上单调递增,
所以 ,所以 ,故 ,即 ,
第5页/共22页
学科网(北京)股份有限公司所以 ,所以 ,故 ,所以 ,
故 ,
设 ,则 ,
令 , ,
当 时, ,函数 单调递减,
当 时, ,函数 单调递增,
又 ,
所以当 时, ,
所以当 时, ,函数 单调递增,
所以 ,即 ,所以
故选:C.
方法二:比较法
解: , , ,
① ,
令
则 ,
故 在 上单调递减,
可得 ,即 ,所以 ;
第6页/共22页
学科网(北京)股份有限公司② ,
令
则 ,
令 ,所以 ,
所以 在 上单调递增,可得 ,即 ,
所以 在 上单调递增,可得 ,即 ,所以
故
二、多项选择题
9. 已知等差数列 是递增数列,且 ,其前 项和为 ,则下列选择项正确的是( )
A. B. 当 时, 取得最小值
C. D. 当 时, 的最小值为8
【答案】ACD
【解析】
【分析】设等差数列 的公差为 ,因为 ,求得 ,根据数列 是递增数列,可判
断AC;由等差数列前 项和公式,结合二次函数的性质和不等式的解法,可判断BD.
【详解】由题意,设等差数列 的公差为 ,
因为 ,可得 ,解得 ,
又由等差数列 是递增数列,得 ,则 ,故AC正确;
因为 ,
第7页/共22页
学科网(北京)股份有限公司由二次函数的性质知,对称轴为 ,开口向上,
所以,当 或4时 最小,故B错误;
令 ,解得 或 ,即 时 的最小值为8,故D正确.
故选:ACD.
10. 下列说法正确的有
A. 在△ABC中,a∶b∶c=sin A∶sin B∶sin C
B. 在△ABC中,若sin 2A=sin 2B,则△ABC为等腰三角形
C. △ABC中,sin A>sin B是A >B的充要条件
D. 在△ABC中,若sin A= ,则A=
【答案】AC
【解析】
【分析】由正弦定理,二倍角的正弦公式,逐一分析各个选项,即可求解.
【详解】由正弦定理
可得:
即 成立,
故选项A正确;
由 可得 或 ,
即 或 ,
则 是等腰三角形或直角三角形,
故选项B错误;
在 中,由正弦定理可得
,
第8页/共22页
学科网(北京)股份有限公司则 是 的充要条件,
故选项C正确;
在△ABC中,若sin A= ,则 或 ,
故选项D错误.
故选:AC.
【点睛】本题考查了命题真假性的判断,正弦定理的应用,属于基础题.
11. 已知函数 ,则( )
A. 是偶函数 B. 在区间 上单调递减
C. 在区间 上有四个零点 D. 的值域为
【答案】ABD
【解析】
【分析】由定义判断A;由正弦函数的单调性判断B;由 在 上的零点结合奇偶性判断C;讨论
的值域,结合奇偶性判断D.
【详解】对于A:其定义域为 , ,即函数 是
偶函数,故A正确;
对于B: 时, ,由正弦函数的单调性可知, 在区间
上单调递减,故B正确;
对于C: 时, ,此时 ,可得 或 ,因
为 是偶函数,所以 在区间 上的零点为 ,故C错误;
第9页/共22页
学科网(北京)股份有限公司对于D:当 ,且 时, .
当 ,且 时, , .
又 是偶函数,所以函数 的值域为 ,故D正确;
故选:ABD
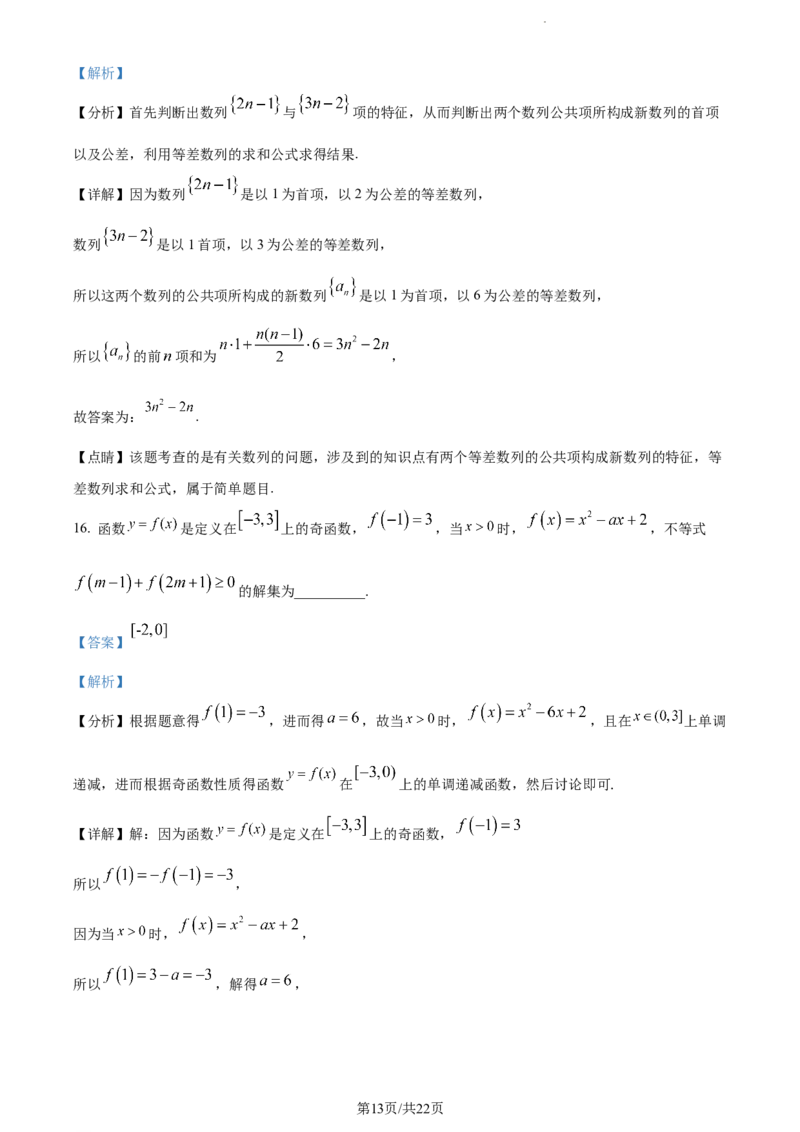
12. 已知函数 , ,使方程 有 4 个不同的解:分别记为
,其中 ,则下列说法正确的是( ).
A. B.
C. D. 的最小值为14
【答案】AC
【解析】
【分析】画出函数图象,利用数形结合思想进行求解判断即可.
【详解】
如图, 时,方程存在4个不同根,
当 时, ,
时, 得
即 ,由正弦函数对称性知 ,
第10页/共22页
学科网(北京)股份有限公司,
在 上单调递增,所以 ;
,
在 上单调递减,所以 ,无最小值,
故选:AC
【点睛】关键点睛:利用数形结合思想进行求解是解题的关键.
三、填空题
13. 已知 在 上的最大值为M,最小值为m,若 ,则 ______.
【答案】−2或−4
【解析】
【分析】根据区间和二次函数对称轴的相对位置,结合二次函数的单调性分类讨论求解即可.
【详解】二次函数 的对称轴为: ,
当 时,即 ,函数在 上单调递增,
所以 ,由 ,得 ,不满足 ,舍去;
当 时,即 时,函数在 上单调递减,
所以 ,由 ,得 ,不满足 ,
舍去,
当 时,则 ,此时 ,
第11页/共22页
学科网(北京)股份有限公司若 时,即 时, ,
由 ,得 ,或 舍去,
若 时,即 , ,
由 ,得 ,或 舍去,
综上所述: 或 ,
故答案为:−2或−4
【点睛】关键点睛:根据二次函数对称轴与所给区间的相对位置分类讨论是解题的关键.
14. 若 ,则 __________ ;
【答案】
【解析】
【分析】由题意, 是 的2倍,根据余弦二倍公式,即可求解.
【详解】由题意
故答案为:
【
点睛】本题考查余弦二倍角公式,属于基础题.
15. 将数列{2n–1}与{3n–2}的公共项从小到大排列得到数列{a},则{a}的前n项和为________.
n n
【答案】
第12页/共22页
学科网(北京)股份有限公司【解析】
【分析】首先判断出数列 与 项的特征,从而判断出两个数列公共项所构成新数列的首项
以及公差,利用等差数列的求和公式求得结果.
【详解】因为数列 是以1为首项,以2为公差的等差数列,
数列 是以1首项,以3为公差的等差数列,
所以这两个数列的公共项所构成的新数列 是以1为首项,以6为公差的等差数列,
所以 的前 项和为 ,
故答案为: .
【点睛】该题考查的是有关数列的问题,涉及到的知识点有两个等差数列的公共项构成新数列的特征,等
差数列求和公式,属于简单题目.
16. 函数 是定义在 上的奇函数, ,当 时, ,不等式
的解集为__________.
【答案】
【解析】
【分析】根据题意得 ,进而得 ,故当 时, ,且在 上单调
递减,进而根据奇函数性质得函数 在 上的单调递减函数,然后讨论即可.
【详解】解:因为函数 是定义在 上的奇函数,
所以 ,
因为当 时, ,
所以 ,解得 ,
第13页/共22页
学科网(北京)股份有限公司所以当 时, ,
当 时,
所以由二次函数的性质得 时,函数 单调递减,在 上单调递减
易知
当 时,原不等式 ,解得 ;
当 时,无实数解;
当 ,无实数解;
当 ,即 时,原不等式
,解得 ;
当 ,即 时, , ,满足题意;
当 ,即 时, , ,不满足题意.
综上,原不等式的解集为:
故答案为:
第14页/共22页
学科网(北京)股份有限公司四、解答题
17. 记 的内角A,B,C的对边分别为a,b,c,已知 .
(1)求C;
(2)若 , ,求 的面积.
【答案】(1)
(2)
【解析】
【分析】(1)由正弦定理和两角和的正弦公式化简即可得答案;
(2)由余弦定理求得a值,然后利用面积公式求解即可.
【小问1详解】
由正弦定理得 ,
得 .
第15页/共22页
学科网(北京)股份有限公司因为 ,所以 ,所以 ,即 .
【小问2详解】
由余弦定理得 ,得 ,
所以 ,故 的面积为 .
18. 问题:设公差不为零的等差数列 的前 项和为 ,且 , .
下列三个条件:① 成等比数列;② ;③ .从上述三个条件中,任选一个
补充在上面的问题中,并解答.
(1)求数列 的通项公式;
(2)若 ,数列 的前 项和为 ,求证: .
【答案】(1)
(2)证明见解析
【解析】
【分析】(1)选①②③分别与 组成方程组,解出首项与公差即可得解;
(2)利用裂项相消法求出数列的前 项和为 ,即可得证.
【小问1详解】
设等差数列 的公差为 .
选条件①:∵ S=6,a,a,a 成等比数列,
3 2 4 8
∴ ,解得 ,
故数列 的通项公式为 .
选条件②:∵ S=6,S=5a,
3 4 2
第16页/共22页
学科网(北京)股份有限公司∴ ,解得 ,
故数列 的通项公式为 .
选条件③:∵ S=6,(n+1)a=na ,
3 n n+1
∴ ,解得 ,
故数列 的通项公式为 .
【小问2详解】
证明:∵ = ,
∴ +…+ =
= .
19. 已知函数 .若函数 在 处有极值-4.
(1)求 的单调递减区间;
(2)求函数 在 上的最大值和最小值.
【答案】(1) ;(2) .
【解析】
【详解】试题分析:
先求出导函数,根据导数的几何意义得到关于 的方程组,求得 后再根据导函数的符号求出单
调递减区间.
由 求出函数的单调区间,可以数判断函数 在 上的单调性,求出函数 在
上的极值和端点值,通过比较可得 的最大值和最小值.
第17页/共22页
学科网(北京)股份有限公司试题解析:
(1)∵ ,
∴ ,
依题意有即 ,解得
∴ ,
由 ,得 ,
∴函数 的单调递减区间
由 知
∴ ,
令 ,解得 .
当 变化时, 的变化情况如下表:
由上表知,函数 在 上单调递减,在 上单调递增.
故可得
又 .
∴
第18页/共22页
学科网(北京)股份有限公司综上可得函数 在 上的最大值和最小值分别为 和 .
20. 已知函数 , .
(1)求 的最小正周期和单调区间;
(2)求 在闭区间 上的最大值和最小值.
【答案】(1)最小正周期为 ,单调递增区间是 ,单调递减区间是
;
(2)最小值为 ,最大值为
【解析】
【分析】(1)由三角函数中的恒等变换应用化简函数解析式可得 ,利用正弦函数的
性质即得;
(2)利用正弦函数的性质即求.
【小问1详解】
由
第19页/共22页
学科网(北京)股份有限公司,
∴ 的最小正周期为 ,
由 ,得 ,
由 ,得
∴函数单调增区间为 ,函数单调减区间为 ;
【小问2详解】
由于 ,
所以 ,
所以 ,
故 ,
故函数的最小值为 ,函数的最大值为 .
21. 已知等差数列 的前 项和为 ,且满足 , .
(1)求数列 的通项公式;
(2)设 ,数列 的前 项和为 ,求 .
【答案】(1) ;(2)
【解析】
【分析】
第20页/共22页
学科网(北京)股份有限公司(1)结合等差数列下标性质可得 ,再由前 项和公式 ,
即可求解;
(2)由(1) ,再结合错位相减法即可求解;
【详解】(1)设数列 的公差为 ,∵ ,∴ ,
,∴ ,
∴ ,∴ .
(2)由(1)可知 ,
∴数列 的前 项和为 ,
,
两式作差,得
,
∴ .
【点睛】本题考查等差数列通项公式的求解,错位相减法求解数列的前 项和,属于中档题
.
22 设函数 .
(Ⅰ)讨论 的导函数 的零点的个数;
.
(Ⅱ)证明:当 时
【答案】(Ⅰ)当 时, 没有零点;当 时, 存在唯一零点.(Ⅱ)见解析
【解析】
第21页/共22页
学科网(北京)股份有限公司【详解】试题分析:(Ⅰ)先求出导函数,分 与 考虑 的单调性及性质,即可判断出零点
个数;(Ⅱ)由(Ⅰ)可设 在 的唯一零点为 ,根据 的正负,即可判定函数的图像
与性质,求出函数的最小值,即可证明其最小值不小于 ,即证明了所证不等式.
试题解析:(Ⅰ) 的定义域为 , .
当 时, , 没有零点;
当 时,因为 单调递增, 单调递增,所以 在 单调递增.又 ,当b满足
且 时, ,故当 时, 存在唯一零点.
(Ⅱ)由(Ⅰ),可设 在 的唯一零点为 ,当 时, ;
当 时, .
故 在 单调递减,在 单调递增,所以当 时, 取得最小值,最小值为 .
由于 ,所以 .
故当 时, .
考点:常见函数导数及导数运算法则;函数的零点;利用导数研究函数图像与性质;利用导数证明不等式;
运算求解能力.
第22页/共22页
学科网(北京)股份有限公司