2004年湖北高考理科数学真题及答案_数学高考真题试卷_旧1990-2007·高考数学真题_1990-2007·高考数学真题·PDF_湖北

2004 年湖北高考理科数学真题及答案 一、选择题（共12小题，每小题5分，满分60分） 1．（5分）与直线2x y40的平行的抛物线yx2的切线方程是( ) A．2x y30 B．2x y30 C．2x y10 D．2x y10 (1 3i)2 2．（5分）复数 的值是( ) 1 3i 1 1 3 A．2 B．16 C． D．  i 4 4 4 1x 1x2 3．（5分）已知 f( ) ，则 f(x)的解析式为( ) 1x 1x2 x 2x A． f(x) B． f(x) 1x2 1x2 2x x C． f(x) D． f(x) 1x2 1x2 4．（5分）已知a,b  ,c为非零的平面向量．甲：a b  a c，乙：b  c，则( )   A．甲是乙的充分条件但不是必要条件 B．甲是乙的必要条件但不是充分条件 C．甲是乙的充要条件 D．甲既不是乙的充分条件也不是乙的必要条件 1 1 5．（5分）若  0，则下列不等式 a b ①abab； ②|a||b|； ③ab； b a ④  2中，正确的不等式有( ) a b A．0个 B．1个 C．2个 D．3个 x2 y2 6．（5分）已知椭圆  1的左、右焦点分别为F 、F ，点P在椭圆上．若P、F 、F 是一个直角三 16 9 1 2 1 2 角形的三个顶点，则点P到x轴的距离为( ) 9 9 7 9 A． B．3 C． D． 5 7 4 7．（5分）函数 f(x)ax log (x1)在[0，1]上的最大值与最小值的和为a，则a的值为( ) a 第1页 | 共19页1 1 A． B． C．2 D．4 4 2 1 1 8．（5分）已知数列{a }的前n项和S a[2( )n1]b[2(n1)( )n1](n1,2,)，其中a、b是非零常数， n n 2 2 则存在数列{x }、{y }使得( ) n n A．a x  y ，其中{x }为等差数列，{y }为等比数列 n n n n n B．a x  y ，其中{x }和{y }都为等差数列 n n n n n C．a x y ，其中{x }为等差数列，{y }都为等比数列 n n n n n D．a x y ，其中{x }和{y }都为等比数列 n n n n n 9．（5分）函数 f(x)ax3 x1有极值的充要条件是( ) A．a0 B．a…0 C．a0 D．a„ 0 10．（5分）设集合P{m|1m0}，Q{mR|mx2 4mx40对任意实数x恒成立}，则下列关系中 成立的是( ) A．PÜQ B．QÜP C．PQ D．P QQ  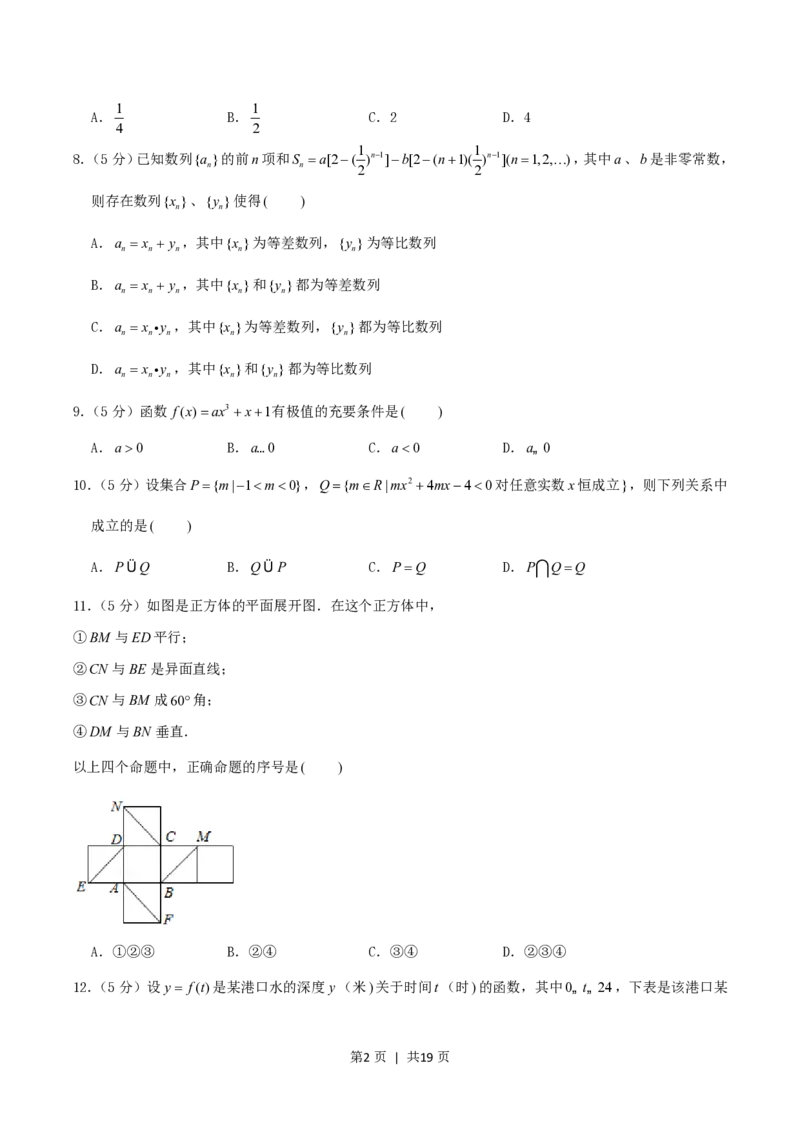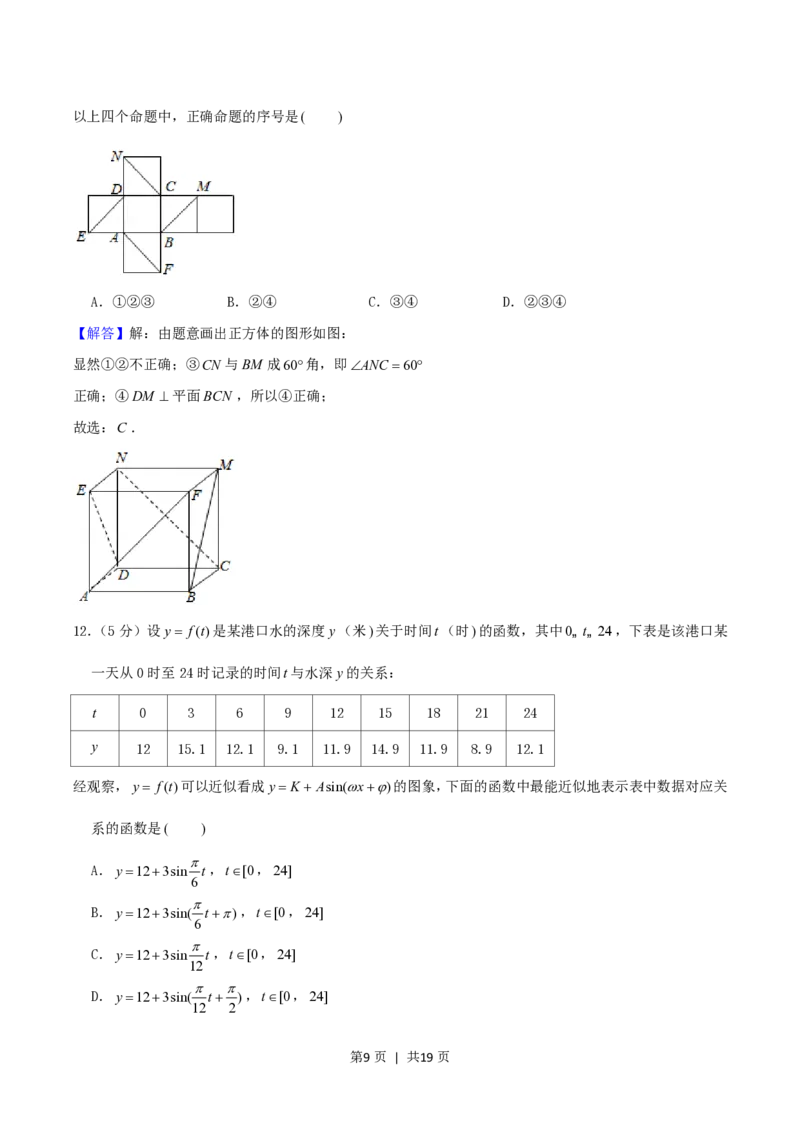11．（5分）如图是正方体的平面展开图．在这个正方体中， ①BM 与ED平行； ②CN 与BE 是异面直线； ③CN 与BM 成60角； ④DM 与BN 垂直． 以上四个命题中，正确命题的序号是( ) A．①②③ B．②④ C．③④ D．②③④ 12．（5分）设y f(t)是某港口水的深度y（米)关于时间t（时)的函数，其中0„ t„ 24，下表是该港口某 第2页 | 共19页一天从0时至24时记录的时间t与水深y的关系： t 0 3 6 9 12 15 18 21 24 y 12 15.1 12.1 9.1 11.9 14.9 11.9 8.9 12.1 经观察，y f(t)可以近似看成yK  Asin(x)的图象，下面的函数中最能近似地表示表中数据对应关 系的函数是( )  A．y123sin t，t[0，24] 6  B．y123sin( t)，t[0，24] 6  C．y123sin t，t[0，24] 12   D．y123sin( t )，t[0，24] 12 2 二、填空题（共4小题，每小题4分，满分16分） a 13．（4分）设随机变量的概率分布为Pk ,a为常数,k 1,2,,则a ． 5k 14．（4分）将标号为1，2，，10的10个球放入标号为1，2，，10的10个盒子内，每个盒内放一个 球，则恰好有3个球的标号与其所在盒子的标号不一致的放入方法共有 种．（以数字作答） 15．（4分）设A、B为两个集合．下列四个命题： ①Aà B对任意xA，有xB； ②Aà B A B；  ③Aà B Aá B； ④Aà B存在xA，使得xB． 其中真命题的序号是 ．（把符合要求的命题序号都填上） 16．（4 分）某日中午 12 时整，甲船自 A处以16km/h的速度向正东行驶，乙船自 A的正北18km处以 24km/h的速度向正南行驶，则当日12时30分时两船之间距间对时间的变化率是 km/h． 三、解答题（共6小题，满分74分）   17．（12分）已知6sin2sincos2cos20，[ ，]，求sin(2 )的值． 2 3 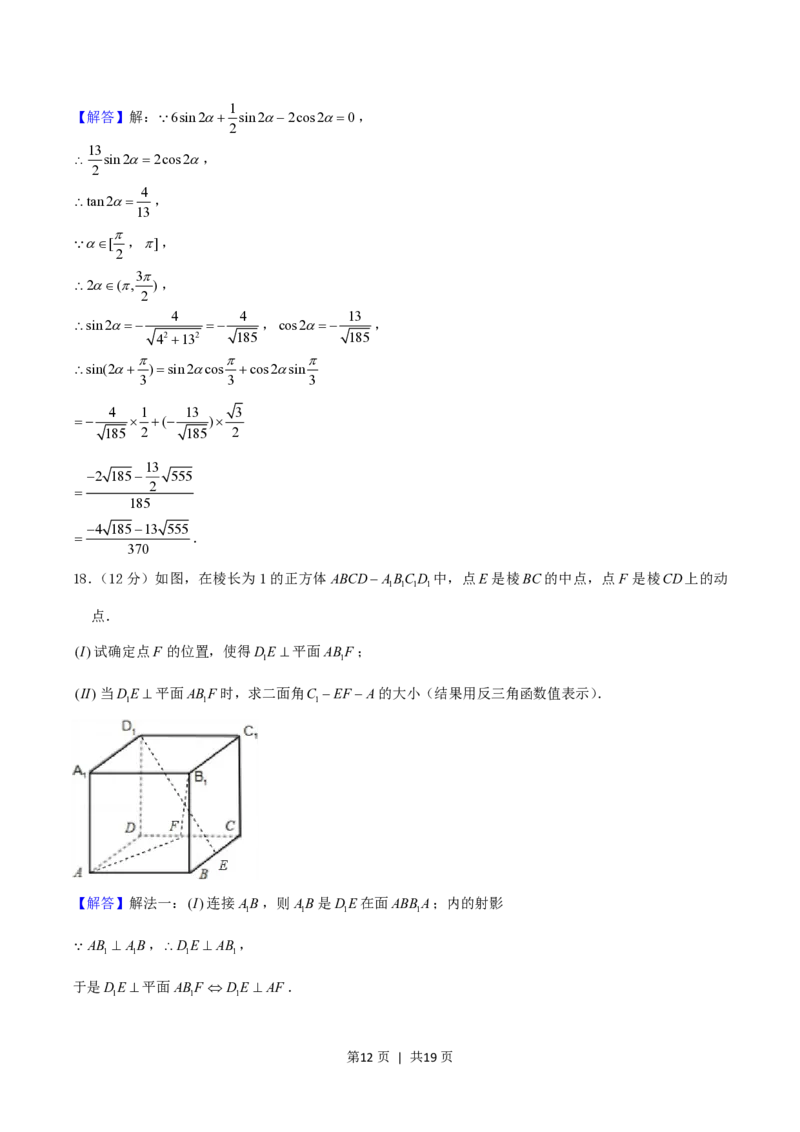18．（12分）如图，在棱长为1的正方体ABCDABCD 中，点E是棱BC的中点，点F 是棱CD上的动 1 1 1 1 点． 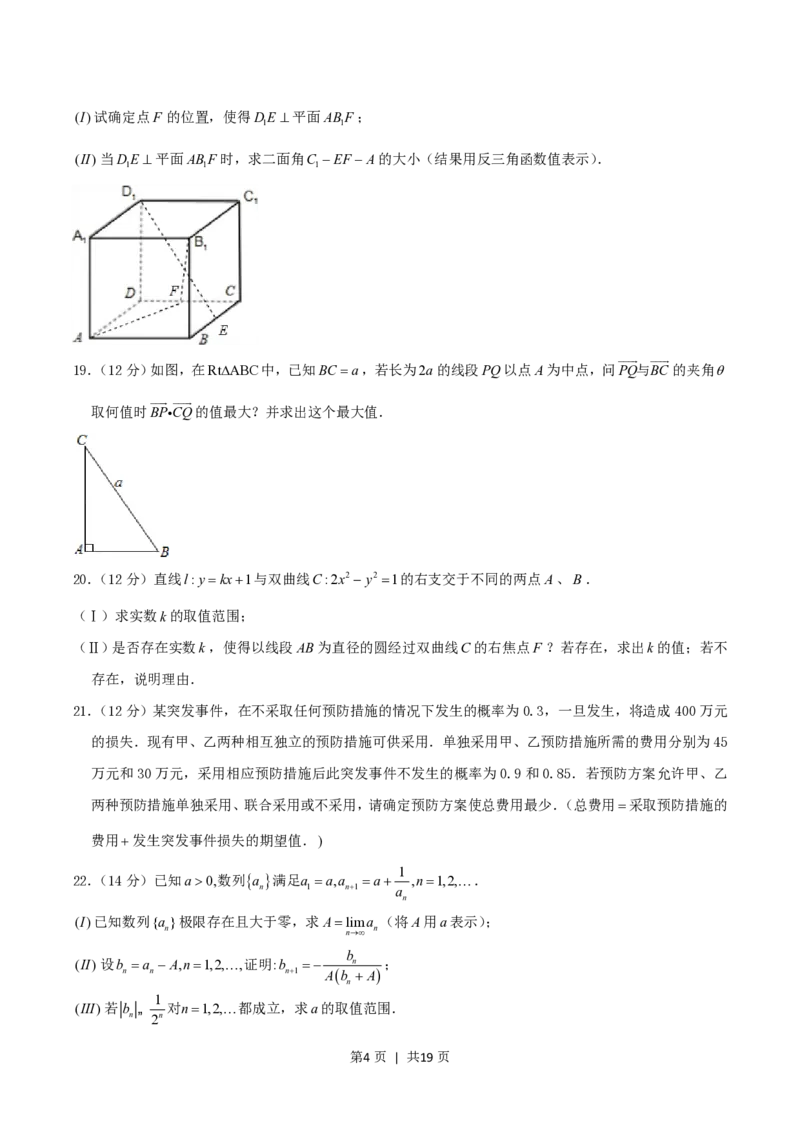第3页 | 共19页(I)试确定点F 的位置，使得DE平面ABF； 1 1 (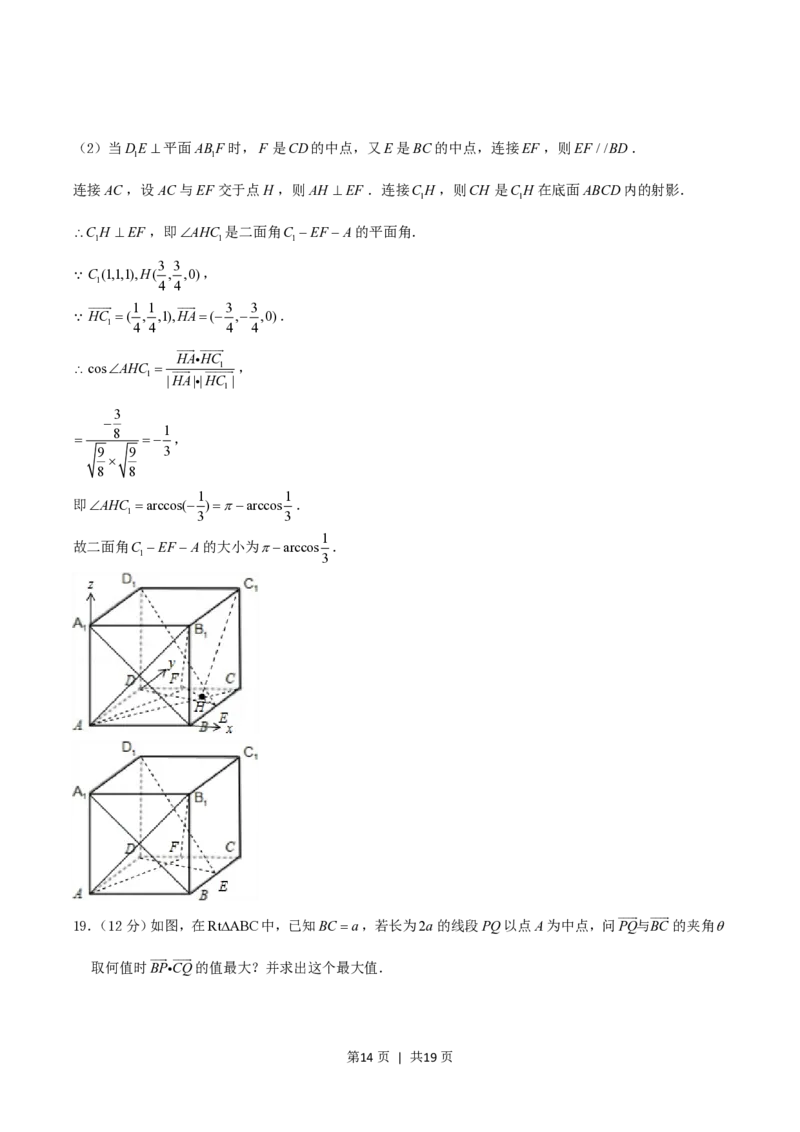II)当DE平面ABF时，求二面角C EF A的大小（结果用反三角函数值表示）． 1 1 1   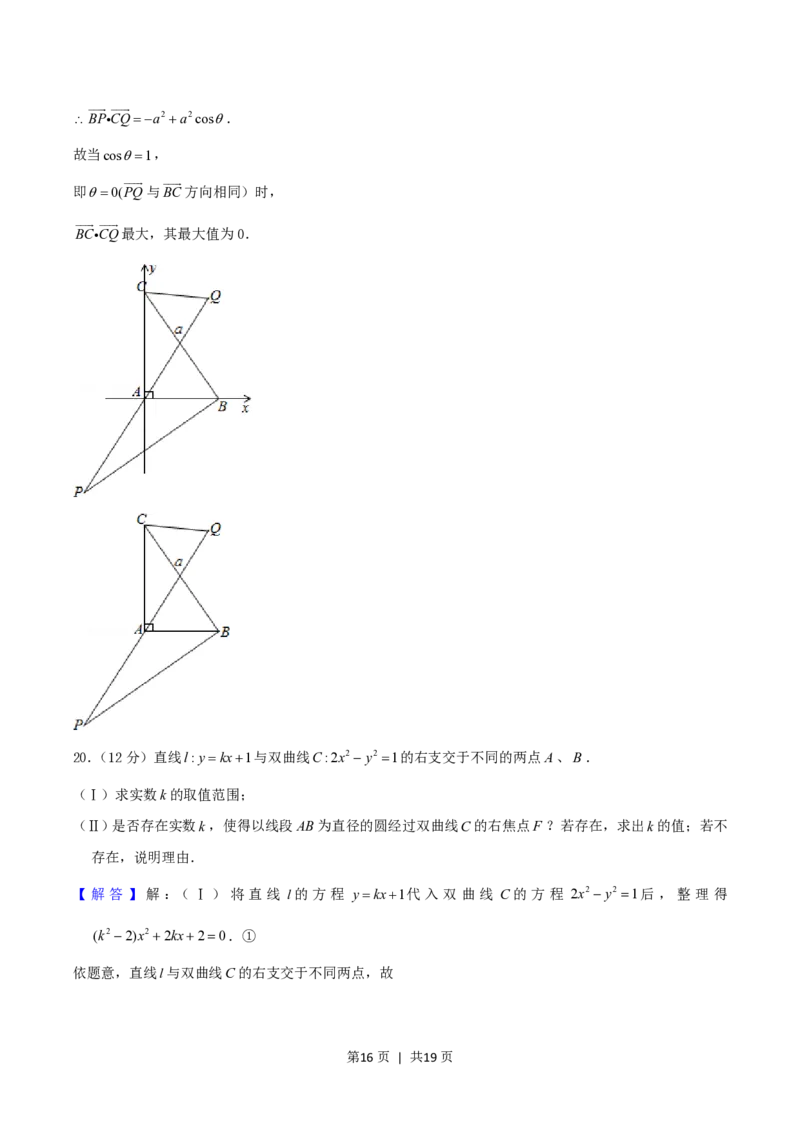19．（12分）如图，在RtABC中，已知BC a，若长为2a的线段PQ以点A为中点，问PQ与BC的夹角   取何值时BP CQ的值最大？并求出这个最大值．  20．（12分）直线l:ykx1与双曲线C:2x2  y2 1的右支交于不同的两点A、B． （Ⅰ）求实数k的取值范围； （Ⅱ）是否存在实数k，使得以线段AB为直径的圆经过双曲线C的右焦点F ？若存在，求出k的值；若不 存在，说明理由． 21．（12分）某突发事件，在不采取任何预防措施的情况下发生的概率为0.3，一旦发生，将造成400万元 的损失．现有甲、乙两种相互独立的预防措施可供采用．单独采用甲、乙预防措施所需的费用分别为45 万元和30万元，采用相应预防措施后此突发事件不发生的概率为0.9和0.85．若预防方案允许甲、乙 两种预防措施单独采用、联合采用或不采用，请确定预防方案使总费用最少．（总费用采取预防措施的 费用发生突发事件损失的期望值．) 1 22．（14分）已知a0,数列a 满足a a,a a ,n1,2,． n 1 n1 a n (I)已知数列{a }极限存在且大于零，求Alima （将A用a表示）； n n n b (II)设b a A,n1,2,,证明:b  n ； n n n1 Ab  A n 1 (III)若 b „ 对n1,2,都成立，求a的取值范围． n 2n 第4页 | 共19页2004年湖北省高考数学试卷（理科） 参考答案与试题解析 一、选择题（共12小题，每小题5分，满分60分） 1．（5分）与直线2x y40的平行的抛物线yx2的切线方程是( ) A．2x y30 B．2x y30 C．2x y10 D．2x y10 【解答】解：由题意可设切线方程为2x ym0 2x ym0 联立方程组 得x2 2xm0 yx2 △44m0解得m1， 切线方程为2x y10， 故选：D． (1 3i)2 2．（5分）复数 的值是( ) 1 3i 1 1 3 A．2 B．16 C． D．  i 4 4 4 (1 3i)2 22 3i 【解答】解：复数  2 1 3i 1 3i 故选：A． 1x 1x2 3．（5分）已知 f( ) ，则 f(x)的解析式为( ) 1x 1x2 x 2x A． f(x) B． f(x) 1x2 1x2 2x x C． f(x) D． f(x) 1x2 1x2 1x 【解答】解：令 t， 1x 1t 得x ， 1t 1t 1( )2 1t 2t f(t)  ， 1t 1t2 1( )2 1t 第5页 | 共19页2x f(x) ． 1x2 故选：C． 4．（5分）已知a,b  ,c为非零的平面向量．甲：a b  a c，乙：b  c，则( )   A．甲是乙的充分条件但不是必要条件 B．甲是乙的必要条件但不是充分条件 C．甲是乙的充要条件 D．甲既不是乙的充分条件也不是乙的必要条件 【解答】解：命题甲：a ba ca (bc)0a0（舍去）或bc或a(bc)．    命题乙：bc，因而乙甲，但甲 乙． 故甲是乙的必要条件但不是充分条件． 故选：B． 1 1 5．（5分）若  0，则下列不等式 a b ①abab； ②|a||b|； ③ab； b a ④  2中，正确的不等式有( ) a b A．0个 B．1个 C．2个 D．3个 1 1 【解答】解：  0，ba0，ab0ab，故①正确．  a b ba0，则|b||a|，故②错误． ③显然错误． b a b a b a 由于 0， 0，  2 2，故④正确．  a b a b a b 综上，①④正确，②③错误， 故选：C． x2 y2 6．（5分）已知椭圆  1的左、右焦点分别为F 、F ，点P在椭圆上．若P、F 、F 是一个直角三 16 9 1 2 1 2 角形的三个顶点，则点P到x轴的距离为( ) 第6页 | 共19页9 9 7 9 A． B．3 C． D． 5 7 4 【解答】解：设椭圆短轴的一个端点为M ． 由于a4，b3， c 7 b FMF 90， 1 2 只能PFF 90或PF F 90． 1 2 2 1 令x 7得 7 92 y2 9(1 ) ， 16 16 9 | y| ． 4 9 即P到x轴的距离为 ， 4 故选：D． 7．（5分）函数 f(x)ax log (x1)在[0，1]上的最大值与最小值的和为a，则a的值为( ) a 1 1 A． B． C．2 D．4 4 2 【解答】解： f(x)是[0，1]上的增函数或减函数， 故 f(0) f （1）a，即1alog 2alog 21， a a 1 2a1 a ． 2 故选：B． 1 1 8．（5分）已知数列{a }的前n项和S a[2( )n1]b[2(n1)( )n1](n1,2,)，其中a、b是非零常数， n n 2 2 则存在数列{x }、{y }使得( ) n n A．a x  y ，其中{x }为等差数列，{y }为等比数列 n n n n n B．a x  y ，其中{x }和{y }都为等差数列 n n n n n C．a x y ，其中{x }为等差数列，{y }都为等比数列 n n n n n D．a x y ，其中{x }和{y }都为等比数列 n n n n n 第7页 | 共19页【解答】解：当n1时，a S a，当n…2时，a S S 1 1 n n n1 1 1 1 1 a[2( )n1]b[2(n1)( )n1]a[2( )n2]b[2n( )n2] 2 2 2 2 1 1 1 a( )n1b[( )n1n( )n1] 2 2 2 1 [a(n1)b]( )n1， 2 1 a [a(n1)b]( )n1(nN*) n 2 故选：C． 9．（5分）函数 f(x)ax3 x1有极值的充要条件是( ) A．a0 B．a…0 C．a0 D．a„ 0 【解答】解：当a0时，函数 f(x)ax3 x1x1是单调增函数无极值，故排除B，D 当a0时，函数 f(x)ax3 x1是单调增函数无极值，故排除A， 故选：C． 10．（5分）设集合P{m|1m0}，Q{mR|mx2 4mx40对任意实数x恒成立}，则下列关系中 成立的是( ) A．PÜQ B．QÜP C．PQ D．P QQ  【解答】解：Q{mR|mx2 4mx40对任意实数x恒成立}， 对m分类：①m0时，40恒成立； ②m0时，需△(4m)2 4m(4)0，解得1m0． 综合①②知m„ 0，Q{mR|1m„ 0}． P{m|1m0}， 故选：A． 11．（5分）如图是正方体的平面展开图．在这个正方体中， ①BM 与ED平行； ②CN 与BE 是异面直线； ③CN 与BM 成60角； ④DM 与BN 垂直． 第8页 | 共19页以上四个命题中，正确命题的序号是( ) A．①②③ B．②④ C．③④ D．②③④ 【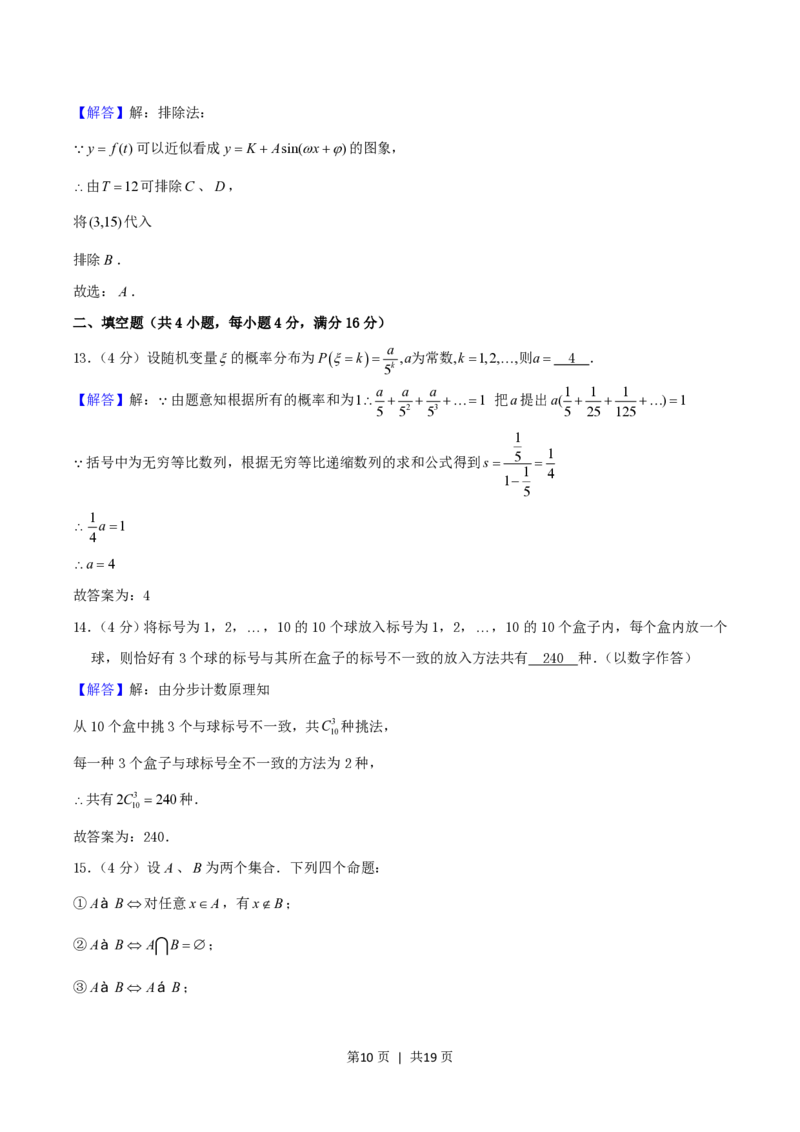解答】解：由题意画出正方体的图形如图： 显然①②不正确；③CN 与BM 成60角，即ANC 60 正确；④DM 平面BCN ，所以④正确； 故选：C． 12．（5分）设y f(t)是某港口水的深度y（米)关于时间t（时)的函数，其中0„ t„ 24，下表是该港口某 一天从0时至24时记录的时间t与水深y的关系： t 0 3 6 9 12 15 18 21 24 y 12 15.1 12.1 9.1 11.9 14.9 11.9 8.9 12.1 经观察，y f(t)可以近似看成yK  Asin(x)的图象，下面的函数中最能近似地表示表中数据对应关 系的函数是( )  A．y123sin t，t[0，24] 6  B．y123sin( t)，t[0，24] 6  C．y123sin t，t[0，24] 12   D．y123sin( t )，t[0，24] 12 2 第9页 | 共19页【解答】解：排除法： y f(t)可以近似看成yK  Asin(x)的图象，  由T 12可排除C、D， 将(3,15)代入 排除B． 故选：A． 二、填空题（共4小题，每小题4分，满分16分） a 13．（4分）设随机变量的概率分布为Pk ,a为常数,k 1,2,,则a 4 ． 5k a a a 1 1 1 【解答】解： 由题意知根据所有的概率和为1   1 把a提出a(   )1  5 52 53 5 25 125 1 5 1 括号中为无穷等比数列，根据无穷等比递缩数列的求和公式得到s   1 4 1 5 1  a1 4 a4 故答案为：4 14．（4分）将标号为1，2，，10的10个球放入标号为1，2，，10的10个盒子内，每个盒内放一个 球，则恰好有3个球的标号与其所在盒子的标号不一致的放入方法共有 240 种．（以数字作答） 【解答】解：由分步计数原理知 从10个盒中挑3个与球标号不一致，共C3 种挑法， 10 每一种3个盒子与球标号全不一致的方法为2种， 共有2C3 240种． 10 故答案为：240． 15．（4分）设A、B为两个集合．下列四个命题： ①Aà B对任意xA，有xB； ②Aà B A B；  ③Aà B Aá B； 第10页 | 共19页④Aà B存在xA，使得xB． 其中真命题的序号是 ④ ．（把符合要求的命题序号都填上） 【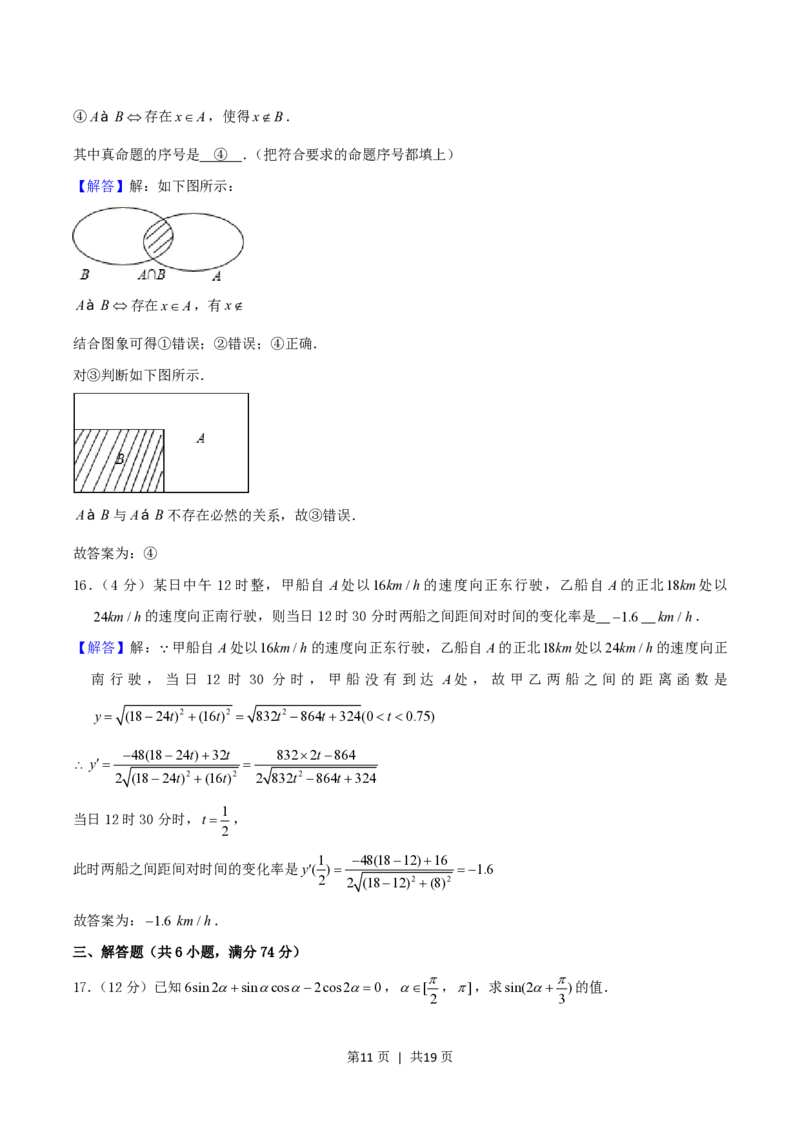解答】解：如下图所示： Aà B存在xA，有x 结合图象可得①错误；②错误；④正确． 对③判断如下图所示． Aà B与Aá B不存在必然的关系，故③错误． 故答案为：④ 16．（4 分）某日中午 12 时整，甲船自 A处以16km/h的速度向正东行驶，乙船自 A的正北18km处以 24km/h的速度向正南行驶，则当日12时30分时两船之间距间对时间的变化率是 1.6 km/h． 【解答】解： 甲船自A处以16km/h的速度向正东行驶，乙船自A的正北18km处以24km/h的速度向正  南 行 驶 ， 当 日 12 时 30 分 时 ， 甲 船 没 有 到 达 A处 ， 故 甲 乙 两 船 之 间 的 距 离 函 数 是 y (1824t)2 (16t)2  832t2 864t324(0t0.75) 48(1824t)32t 8322t864  y  2 (1824t)2 (16t)2 2 832t2 864t324 1 当日12时30分时，t ， 2 1 48(1812)16 此时两船之间距间对时间的变化率是y( ) 1.6 2 2 (1812)2 (8)2 故答案为：1.6 km/h． 三、解答题（共6小题，满分74分）   17．（12分）已知6sin2sincos2cos20，[ ，]，求sin(2 )的值． 2 3 第11页 | 共19页1 【解答】解： 6sin2 sin22cos20，  2 13  sin22cos2， 2 4 tan2 ， 13  [ ，]，  2 3 2(, )， 2 4 4 13 sin2  ，cos2 ， 42 132 185 185    sin(2 )sin2cos cos2sin 3 3 3 4 1 13 3   ( ) 185 2 185 2 13 2 185 555 2  185 4 18513 555  ． 370 18．（12分）如图，在棱长为1的正方体ABCDABCD 中，点E是棱BC的中点，点F 是棱CD上的动 1 1 1 1 点． (I)试确定点F 的位置，使得DE平面ABF； 1 1 (II)当DE平面ABF时，求二面角C EF A的大小（结果用反三角函数值表示）． 1 1 1 【解答】解法一：(I)连接AB，则AB是DE在面ABB A；内的射影 1 1 1 1 AB  AB，DE AB ，  1 1 1 1 于是DE平面ABF  DE AF． 1 1 1 第12页 | 共19页连接DE，则DE是DE在底面ABCD内的射影． 1 DE AF  DE AF ． 1 ABCD是正方形，E是BC的中点．  当且仅当F 是CD的中点时，DE AF， 即当点F 是CD的中点时，DE平面ABF．（6分） 1 1 (II)当DE平面ABF时，由(I)知点F 是CD的中点． 1 1 又已知点E是BC的中点，连接EF ，则EF //BD．连接AC， 设AC与EF 交于点H ，则CH EF ，连接CH，则CH 是 1 CH在底面ABCD内的射影． 1 CH EF，即CHC是二面角C EF C的平面角． 1 1 1 1 2 在Rt△CCH 中， CC 1，CH  AC  ， 1  1 4 4 CC 1 tanCHC  1  2 2． 1 CH 2 4 CHC arctan2 2，从而AHC arctan2 2 ． 1 1 故二面角C EF A的大小为arctan2 2． 1 解法二：以A为坐标原点，建立如图所示的空间直角坐标系 （1）设DF x，则A(0，0，0)，B(1，0，0)，D(0，1，0)， 1 A(0， 0 ， 1)， B(1， 0 ， 1)， D(0， 1 ， 1)， E(1, ,0)， F(x， 1 ， 1 1 2  1   0)DE(1, ,1),AB (1,0,1),AF (x,1,0) 1 2 1   DE AB 110，即DE AB 1  1 1 1   1 于是DE平面ABF  DE AF  DE AF 0 x 0 1 1 1  1  2 1 即x ．故当点F 是CD的中点时，DE平面ABF 2 1 1 第13页 | 共19页（2）当DE平面ABF时，F 是CD的中点，又E是BC的中点，连接EF ，则EF //BD． 1 1 连接AC，设AC与EF 交于点H ，则AH EF ．连接CH，则CH 是CH在底面ABCD内的射影． 1 1 CH EF ，即AHC 是二面角C EF A的平面角． 1 1 1 3 3 C (1,1,1),H( , ,0)，  1 4 4  1 1  3 3 HC ( , ,1),HA( , ,0)．  1 4 4 4 4   HA HC cosAHC   1 ， 1 |  H  A  ||  H  C  |  1 3  8 1   ， 9 9 3  8 8 1 1 即AHC arccos( )arccos ． 1 3 3 1 故二面角C EF A的大小为arccos ． 1 3   19．（12分）如图，在RtABC中，已知BC a，若长为2a的线段PQ以点A为中点，问PQ与BC的夹角   取何值时BP CQ的值最大？并求出这个最大值．  第14页 | 共19页【解答】解：如下图所示：     解法一： AB AC， AB AC 0．           APAQ,BP APAB,CQ AQAC，        BP CQ(APAB) (AQAC)            AP AQAP ACAB AQ AB AC         a2 AP AC AB AP   1  a2  PQ BC  2 a2 a2cos．     故当cos1，即0(PQ与BC方向相同）时，BP CQ最大．其最大值为0．  解法二：以直角顶点A为坐标原点，两直角边所在直线为坐标轴建立如图所示的平面直角坐标系． 设|AB|c|AC|b，则A(0,0)，B(c,0)，C(0,b)， 且|PQ|2a，|BC|a． 设点P的坐标为(x,y)，则Q(x,y)．   BP(xc,y),CQ(x,yb)，   BC (c,b),PQ(2x,2y)．   BP CQ(xc)(x) y(yb)  (x2  y2)cxby．   PQ BC cxby cos   ．    |PQ||BC| a2  cxbya2cos． 第15页 | 共19页  BP CQa2 a2cos．  故当cos1，   即0(PQ与BC方向相同）时，   BC CQ最大，其最大值为0．  20．（12分）直线l:ykx1与双曲线C:2x2  y2 1的右支交于不同的两点A、B． （Ⅰ）求实数k的取值范围； （Ⅱ）是否存在实数k，使得以线段AB为直径的圆经过双曲线C的右焦点F ？若存在，求出k的值；若不 存在，说明理由． 【 解 答 】 解 ：（ Ⅰ ） 将 直 线 l的 方 程 ykx1代 入 双 曲 线 C的 方 程 2x2  y2 1后 ， 整 理 得 (k2 2)x2 2kx20．① 依题意，直线l与双曲线C的右支交于不同两点，故 第16页 | 共19页k2 20  (2k)2 8(k2 2)0   2k  0  k2 2  2  0. k2 2 解得k的取值范围是2k  2．  2k x x    1 2 2k2 （Ⅱ）设A、B两点的坐标分别为(x ，y )、(x ，y )，则由①式得 ② 1 1 2 2 2 x x  .  1 2 k2 2 假设存在实数k，使得以线段AB为直径的圆经过双曲线C的右焦点F(c,0)． 则由FAFB得：(x c)(x c) y y 0． 1 2 1 2 即(x c)(x c)(kx 1)(kx 1)0． 1 2 1 2 整理得(k2 1)xx (kc)(x x )c2 10．③ 1 2 1 2 6 把②式及c 代入③式化简得5k2 2 6k60． 2 解得k  6 6 或k  6 6   2, 2 舍去 5 5 6 6 可知k  使得以线段AB为直径的圆经过双曲线C的右焦点． 5 21．（12分）某突发事件，在不采取任何预防措施的情况下发生的概率为0.3，一旦发生，将造成400万元 的损失．现有甲、乙两种相互独立的预防措施可供采用．单独采用甲、乙预防措施所需的费用分别为45 万元和30万元，采用相应预防措施后此突发事件不发生的概率为0.9和0.85．若预防方案允许甲、乙 两种预防措施单独采用、联合采用或不采用，请确定预防方案使总费用最少．（总费用采取预防措施的 费用发生突发事件损失的期望值．) 【解答】解：①不采取预防措施时，总费用即损失期望为4000.3120（万元）； ②若单独采取措施甲，则预防措施费用为45万元，发生突发事件的概率为 10.90.1，损失期望值为4000.140（万元），所以总费用为454085（万元） ③若单独采取预防措施乙，则预防措施费用为30万元，发生突发事件的概率为10.850.15，损失期望值 为4000.1560（万元），所以总费用为306090（万元）； ④若联合采取甲、乙两种预防措施，则预防措施费用为453075（万元），发生突发事件的概率为 (10.9)(10.85)0.015，损失期望值为4000.0156（万元），所以总费用为75681（万元）． 第17页 | 共19页综合①、②、③、④，比较其总费用可知，应选择联合采取甲、乙两种预防措施，可使总费用最少． 1 22．（14分）已知a0,数列a 满足a a,a a ,n1,2,． n 1 n1 a n (I)已知数列{a }极限存在且大于零，求Alima （将A用a表示）； n n n b (II)设b a A,n1,2,,证明:b  n ； n n n1 Ab  A n 1 (III)若 b „ 对n1,2,都成立，求a的取值范围． n 2n 【 解 答 】 解 ： (I)由 1 1 a a24 ， \mathoplimlimits a存在,且A\mathoplimlimits a (A0),对a a 两边取极限得Aa ,解得A 又A0 n n n n n1 a A 2 n a a2 4  A ． 2 1 1 1 1 1 b II由a b  A,a a 得b  Aa ．b aA    n ． n n n1 a n1 b  A n1 b  A A b  A A(b  A) n n n n n b 即b  n 对n1,2,都成立 n1 Ab  A n 1 1  1 III令b „ ,得a a a2 4 „ ． 1 2 2 2 1 1 | ( a2 4a)|„ ． 2 2 3  a2 4a„1,解得a… ． 2 3 1 现证明当a… 时,b „ 对n1,2,都成立． 2 n 2n (i)当n1时结论成立（已验证）． 1 b 1 1 (ii)假设当nkk…1时结论成立,即b „ ,那么b  k „  k 2k k1 Ab  A Ab  A 2k k k 1 1 3 故只须证明 „ ,即证Ab  A…2对a… 成立． Ab  A 2 k 2 k a a2 4 2 由于A  ， 2 a2 4a 3 而当a… 时, a2 4a„1，A…2． 2 1  b  A…Ab …2 …1,即Ab  A…2． k k 2k k 第18页 | 共19页3 1 1 1 故当a… 时,b „   ． 2 k1 2 2k 2k1 即nk1时结论成立． 根据(i)和(ii)可知结论对一切正整数都成立． 1 3  故 b n „ 2n 对n1,2,都成立的a的取值范围为  2 ,   ． 声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布 日期：2019/5/23 23:08:08；用户：15217760367；邮箱：15217760367；学号：10888156 第19页 | 共19页