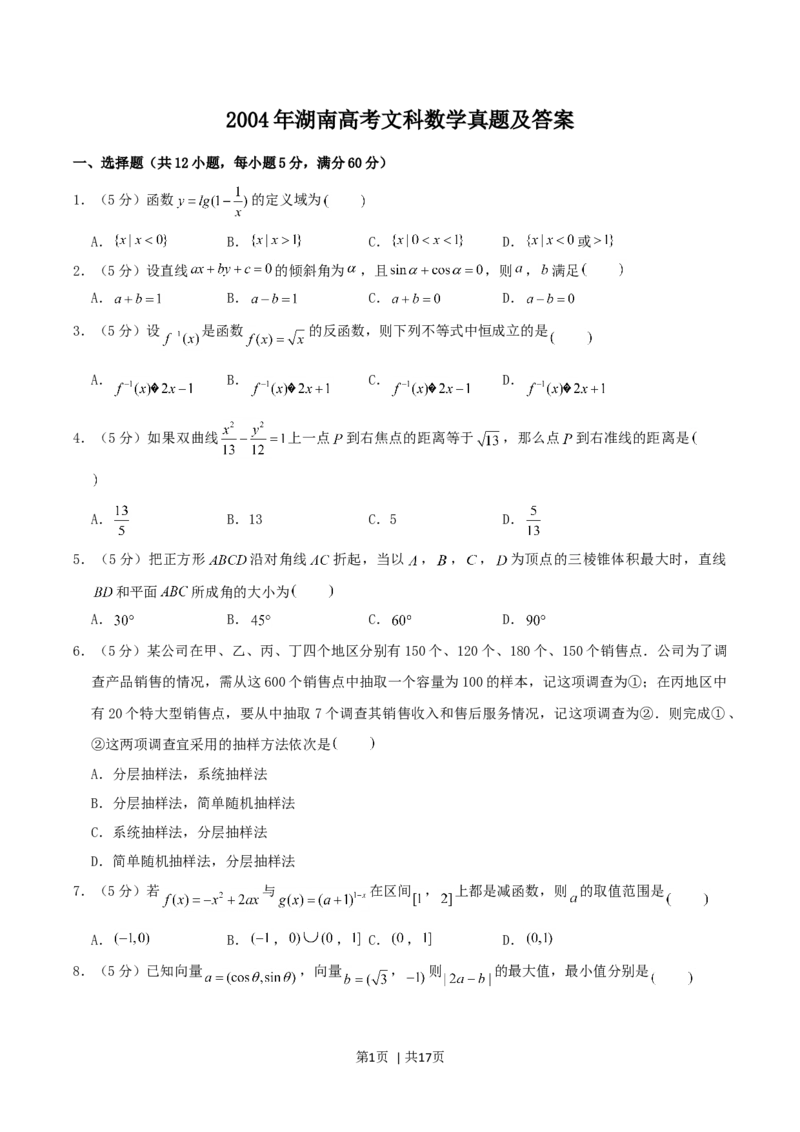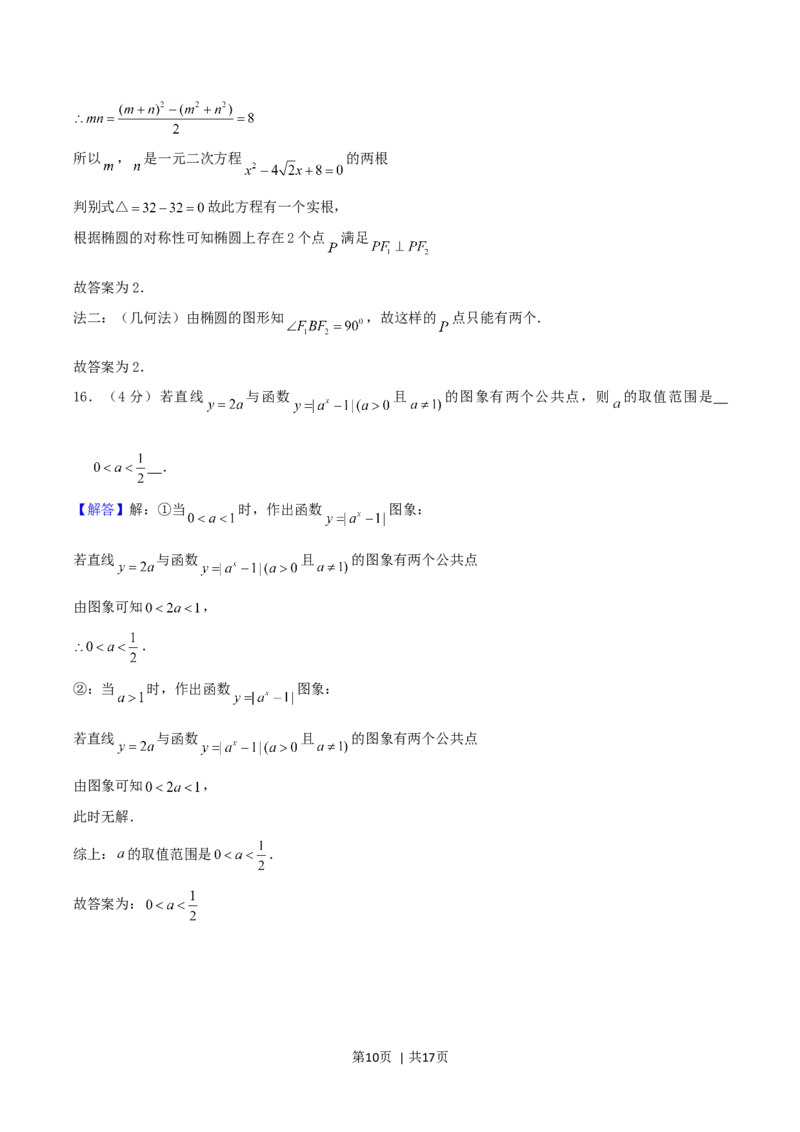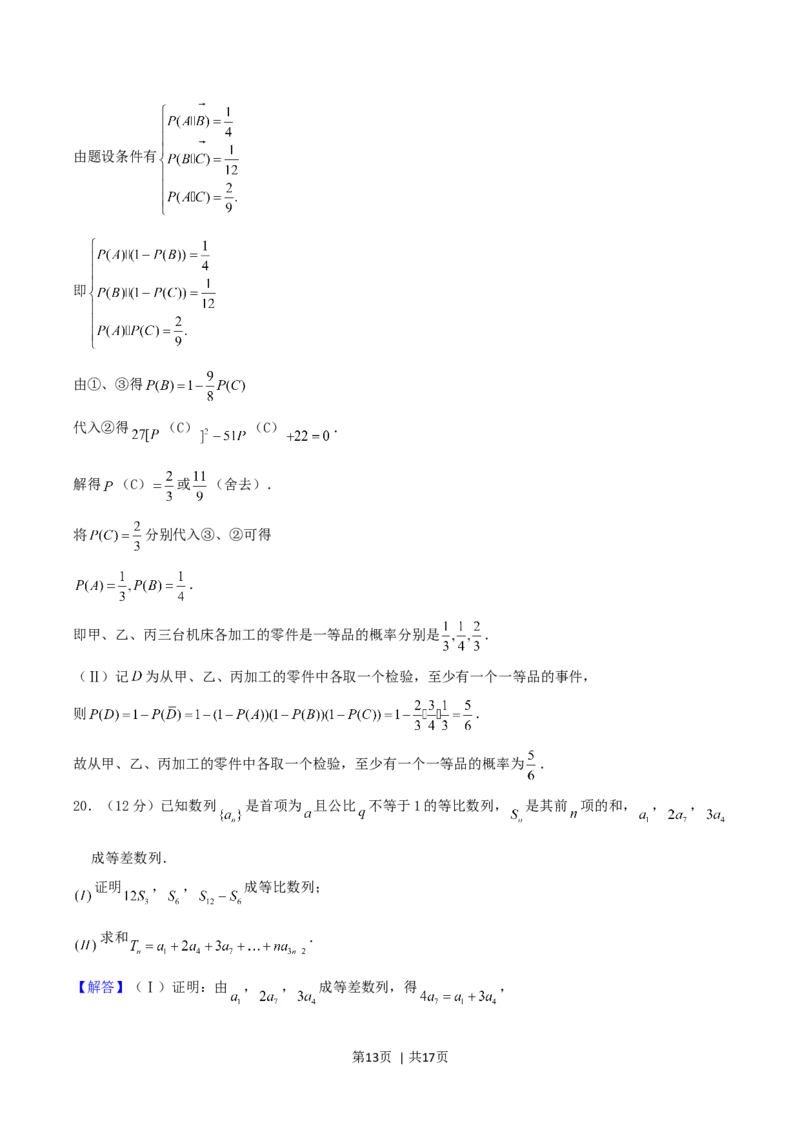文档内容
2004 年湖南高考文科数学真题及答案
一、选择题(共12小题,每小题5分,满分60分)
1.(5分)函数 的定义域为
A. B. C. D. 或
2.(5分)设直线 的倾斜角为 ,且 ,则 , 满足
A. B. C. D.
3.(5分)设 是函数 的反函数,则下列不等式中恒成立的是
A. B. C. D.
4.(5分)如果双曲线 上一点 到右焦点的距离等于 ,那么点 到右准线的距离是
A. B.13 C.5 D.
5.(5分)把正方形 沿对角线 折起,当以 , , , 为顶点的三棱锥体积最大时,直线
和平面 所成角的大小为
A. B. C. D.
6.(5分)某公司在甲、乙、丙、丁四个地区分别有150个、120个、180个、150个销售点.公司为了调
查产品销售的情况,需从这600个销售点中抽取一个容量为100的样本,记这项调查为①;在丙地区中
有20个特大型销售点,要从中抽取7个调查其销售收入和售后服务情况,记这项调查为②.则完成①、
②这两项调查宜采用的抽样方法依次是
A.分层抽样法,系统抽样法
B.分层抽样法,简单随机抽样法
C.系统抽样法,分层抽样法
D.简单随机抽样法,分层抽样法
7.(5分)若 与 在区间 , 上都是减函数,则 的取值范围是
A. B. , , C. , D.
8.(5分)已知向量 ,向量 , 则 的最大值,最小值分别是
第1页 | 共17页A. ,0 B.4, C.16,0 D.4,0
9.(5分)若函数 的图象的顶点在第四象限,则函数 的图象是
A. B.
C. D.
10.(5分)从正方体的八个顶点中任取三个点为顶点作三角形,其中直角三角形的个数为
A.56 B.52 C.48 D.40
11.(5分)农民收入由工资性收入和其它收入两部分构成.2003年某地区农民人均收入为3150元(其中
工资性收入为1800元,其它收入为1350元),预计该地区自2004年起的5年内,农民的工资性收入将
以每年 的年增长率增长,其它收入每年增加160元.根据以上数据,2008年该地区农民人均收入介
于
A.4200元 元 B.4400元 元
C.4600元 元 D.4800元 元
12.(5分)设集合 , , , ,那么
点 , 的充要条件是
A. , B. , C. , D. ,
二、填空题(共4小题,每小题4分,满分16分)
13.(4分)过点 且与曲线 在点 处的切线平行的直线方程是 .
14.(4分) 的展开式中的常数项为 (用数字作答)
15.(4分) , 是椭圆 的焦点,在 上满足 的点 的个数为 .
16.(4分)若直线 与函数 且 的图象有两个公共点,则 的取值范围是 .
第2页 | 共17页三、解答题(共6小题,满分74分)
17.(12分)已知 ,求 的值.
18.(12分)如图,在底面是菱形的四棱锥 中, , , ,
点 是 的中点.
证明 平面 , 平面 ;
求以 为棱, 与 为面的二面角 的正切值.
19.(12分)甲、乙、丙三台机床各自独立地加工同一种零件,已知甲机床加工的零件是一等品而乙机床
加工的零件不是一等品的概率为 ,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率
为 ,甲、丙两台机床加工的零件都是一等品的概率为 .
(Ⅰ)分别求甲、乙、丙三台机床各自加工零件是一等品的概率;
(Ⅱ)从甲、乙、丙加工的零件中各取一个检验,求至少有一个一等品的概率.
20.(12分)已知数列 是首项为 且公比 不等于1的等比数列, 是其前 项的和, , ,
成等差数列.
证明 , , 成等比数列;
求和 .
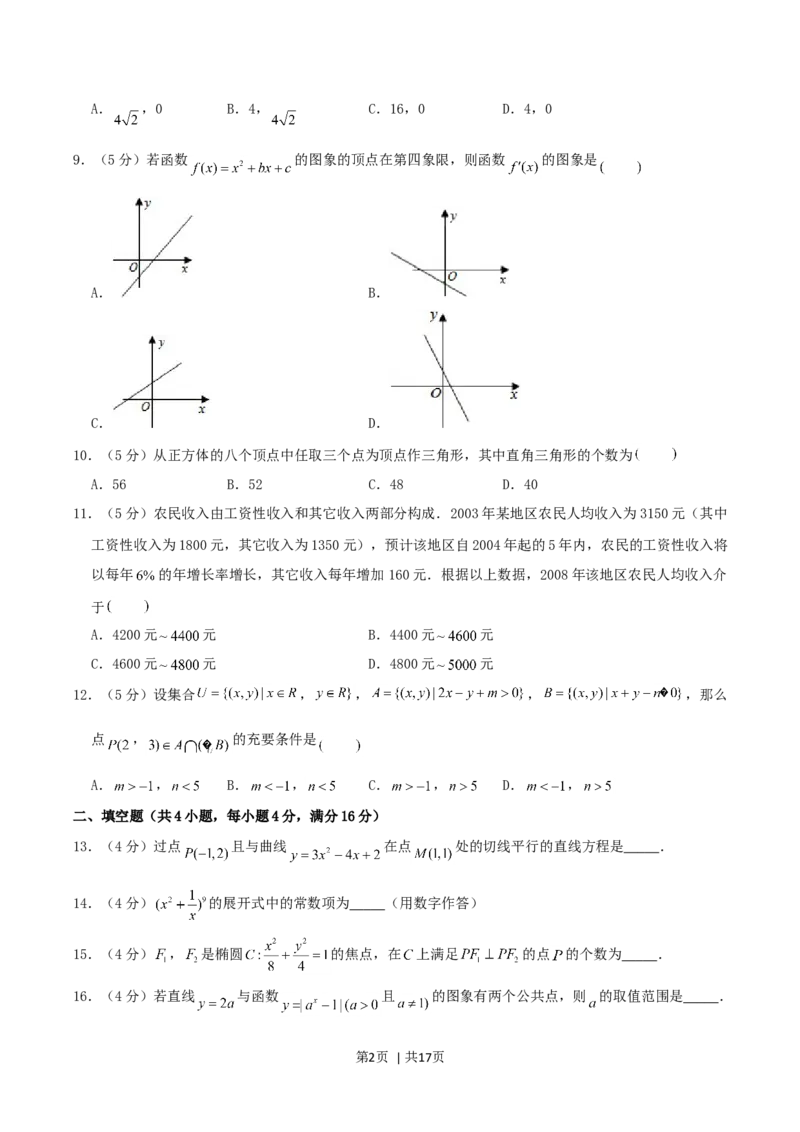
21.(12 分)如图,已知曲线 与曲线 交于 , ,直线
与曲线 , 分别交于 , .
(Ⅰ)写出四边形 的面积 与 的函数关系式 ;
第3页 | 共17页(Ⅱ)讨论 的单调性,并求 的最大值.
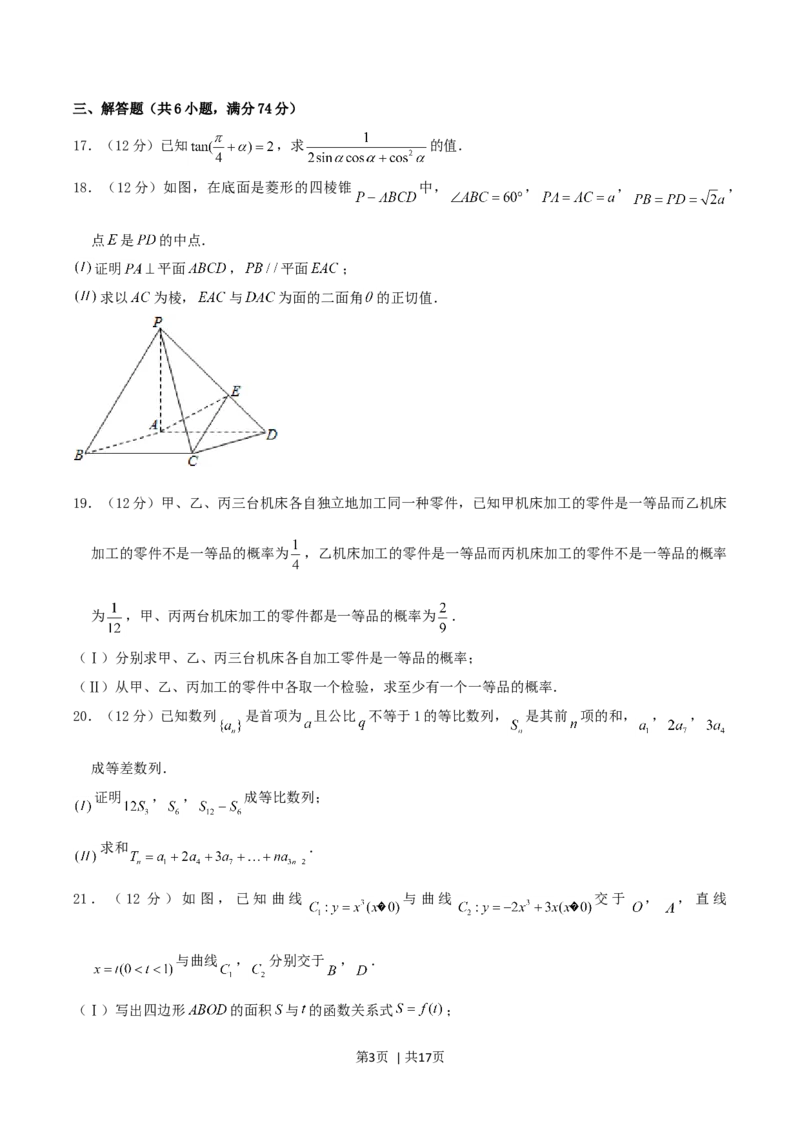
22.(14分)如图,过抛物线 的对称轴上任一点 , 作直线与抛物线交于 , 两点,
点 是点 关于原点的对称点.
设点 分有向线段 所成的比为 ,证明:
(Ⅱ)设直线 的方程是 ,过 , 两点的圆 与抛物线在点 处有共同的切线,求圆
的方程.
第4页 | 共17页2004年湖南省高考数学试卷(文科)
参考答案与试题解析
一、选择题(共12小题,每小题5分,满分60分)
1.(5分)函数 的定义域为
A. B. C. D. 或
【解答】解: ,
或 ,
函数 的定义域: 或 .
故选: .
2.(5分)设直线 的倾斜角为 ,且 ,则 , 满足
A. B. C. D.
【解答】解:
, , , ,
故选: .
3.(5分)设 是函数 的反函数,则下列不等式中恒成立的是
A. B. C. D.
【解答】解:由 解得: ,
则函数 的反函数为 ,
恒成立
不等式中恒成立的是
故选: .
4.(5分)如果双曲线 上一点 到右焦点的距离等于 ,那么点 到右准线的距离是
第5页 | 共17页A. B.13 C.5 D.
【解答】解:由题意可知, ,
点 到左焦点的距离 ,
设点 到右准线的距离是 ,
由双曲线的第二定义可知 ,
解得 ;
故选: .
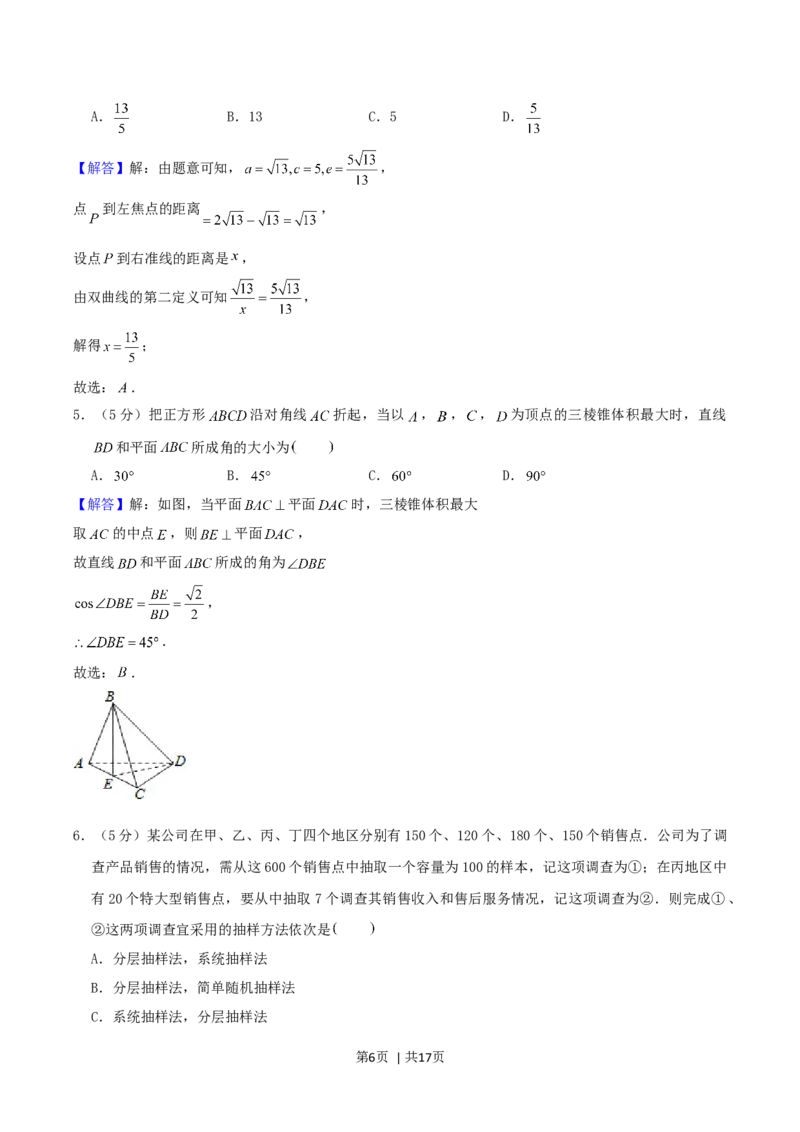
5.(5分)把正方形 沿对角线 折起,当以 , , , 为顶点的三棱锥体积最大时,直线
和平面 所成角的大小为
A. B. C. D.
【解答】解:如图,当平面 平面 时,三棱锥体积最大
取 的中点 ,则 平面 ,
故直线 和平面 所成的角为
,
.
故选: .
6.(5分)某公司在甲、乙、丙、丁四个地区分别有150个、120个、180个、150个销售点.公司为了调
查产品销售的情况,需从这600个销售点中抽取一个容量为100的样本,记这项调查为①;在丙地区中
有20个特大型销售点,要从中抽取7个调查其销售收入和售后服务情况,记这项调查为②.则完成①、
②这两项调查宜采用的抽样方法依次是
A.分层抽样法,系统抽样法
B.分层抽样法,简单随机抽样法
C.系统抽样法,分层抽样法
第6页 | 共17页D.简单随机抽样法,分层抽样法
【解答】解:依据题意,第①项调查中,总体中的个体差异较大,应采用分层抽样法;
第②项调查总体中个体较少,应采用简单随机抽样法.
故选: .
7.(5分)若 与 在区间 , 上都是减函数,则 的取值范围是
A. B. , , C. , D.
【解答】解: 在区间 , 上是减函数,故对称轴 ;
在区间 , 上是减函数,只需 ,即 ,综上可得 .
故选: .
8.(5分)已知向量 ,向量 , 则 的最大值,最小值分别是
A. ,0 B.4, C.16,0 D.4,0
【解答】解: , ,
,最大值为 4,最小值为 0.
故选: .
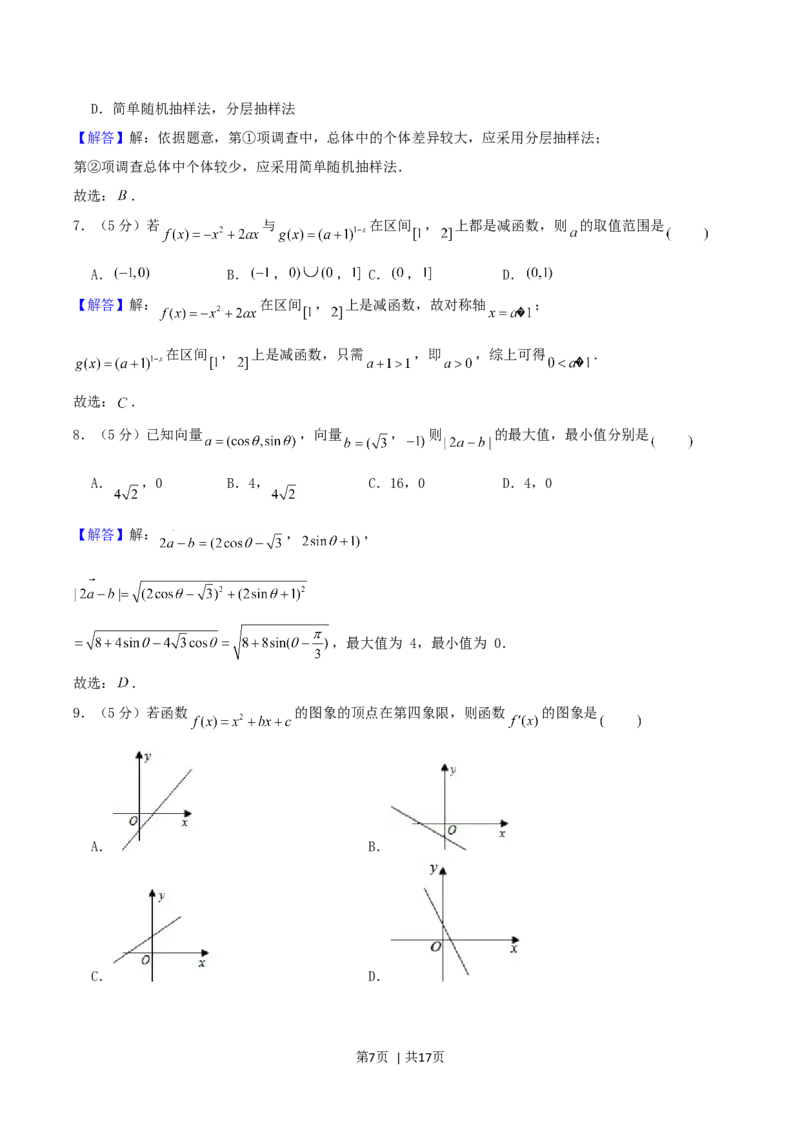
9.(5分)若函数 的图象的顶点在第四象限,则函数 的图象是
A. B.
C. D.
第7页 | 共17页【解答】解:函数 是开口向上的二次函数,顶点在第四象限说明对称轴大于0
根据函数 在对称轴左侧单调递减,导函数小于0;在对称轴右侧单调递增,导函数大于0知, 满足
条件
故选: .
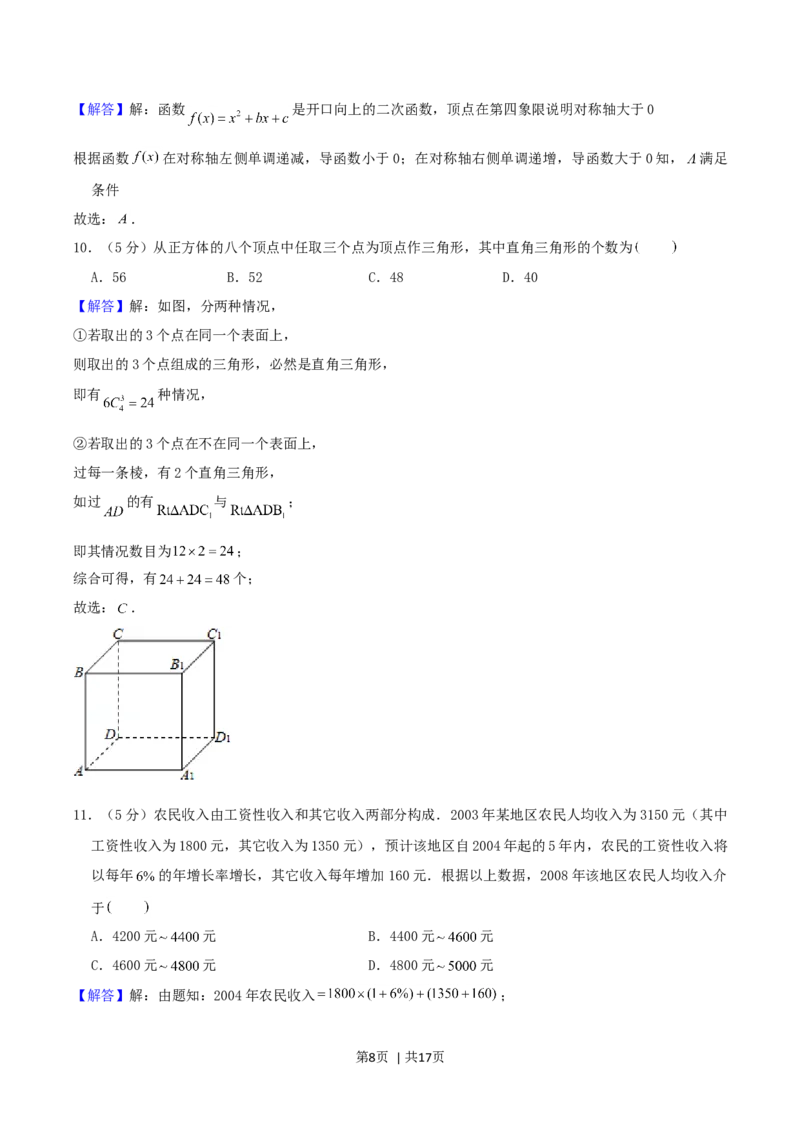
10.(5分)从正方体的八个顶点中任取三个点为顶点作三角形,其中直角三角形的个数为
A.56 B.52 C.48 D.40
【解答】解:如图,分两种情况,
①若取出的3个点在同一个表面上,
则取出的3个点组成的三角形,必然是直角三角形,
即有 种情况,
②若取出的3个点在不在同一个表面上,
过每一条棱,有2个直角三角形,
如过 的有 与 ;
即其情况数目为 ;
综合可得,有 个;
故选: .
11.(5分)农民收入由工资性收入和其它收入两部分构成.2003年某地区农民人均收入为3150元(其中
工资性收入为1800元,其它收入为1350元),预计该地区自2004年起的5年内,农民的工资性收入将
以每年 的年增长率增长,其它收入每年增加160元.根据以上数据,2008年该地区农民人均收入介
于
A.4200元 元 B.4400元 元
C.4600元 元 D.4800元 元
【解答】解:由题知:2004年农民收入 ;
第8页 | 共17页2005年农民收入 ;
所以2008年农民收入
故选: .
12.(5分)设集合 , , , ,那么
点 , 的充要条件是
A. , B. , C. , D. ,
【解答】解:
,
,
,
故选: .
二、填空题(共4小题,每小题4分,满分16分)
13.(4分)过点 且与曲线 在点 处的切线平行的直线方程是
.
【解答】解: , 切线斜率为 . 所求直线方程为 ,即 .
故答案为: .
14.(4分) 的展开式中的常数项为 8 4 (用数字作答)
【解答】解:
令 , ,故 的展开式中的常数项为
故答案为:84
15.(4分) , 是椭圆 的焦点,在 上满足 的点 的个数为 2 .
【解答】解:设 ,
则 ,
第9页 | 共17页所以 , 是一元二次方程 的两根
判别式△ 故此方程有一个实根,
根据椭圆的对称性可知椭圆上存在2个点 满足
故答案为2.
法二:(几何法)由椭圆的图形知 ,故这样的 点只能有两个.
故答案为2.
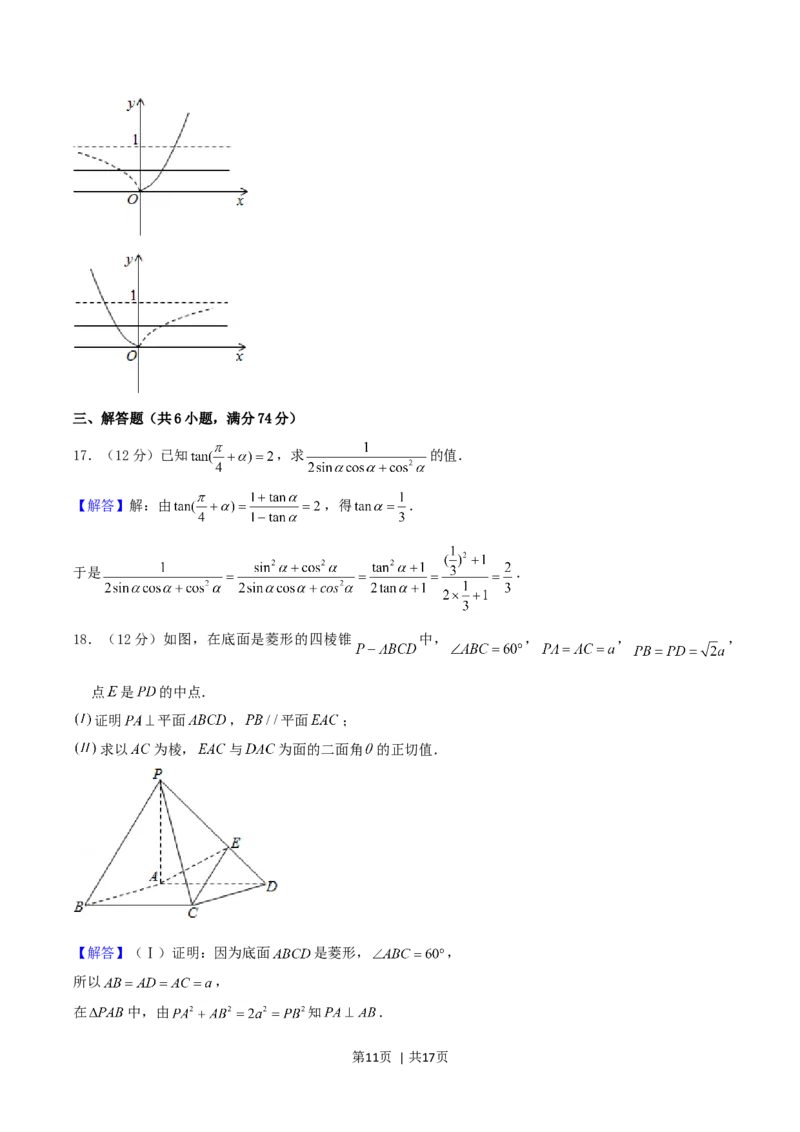
16.(4分)若直线 与函数 且 的图象有两个公共点,则 的取值范围是
.
【解答】解:①当 时,作出函数 图象:
若直线 与函数 且 的图象有两个公共点
由图象可知 ,
.
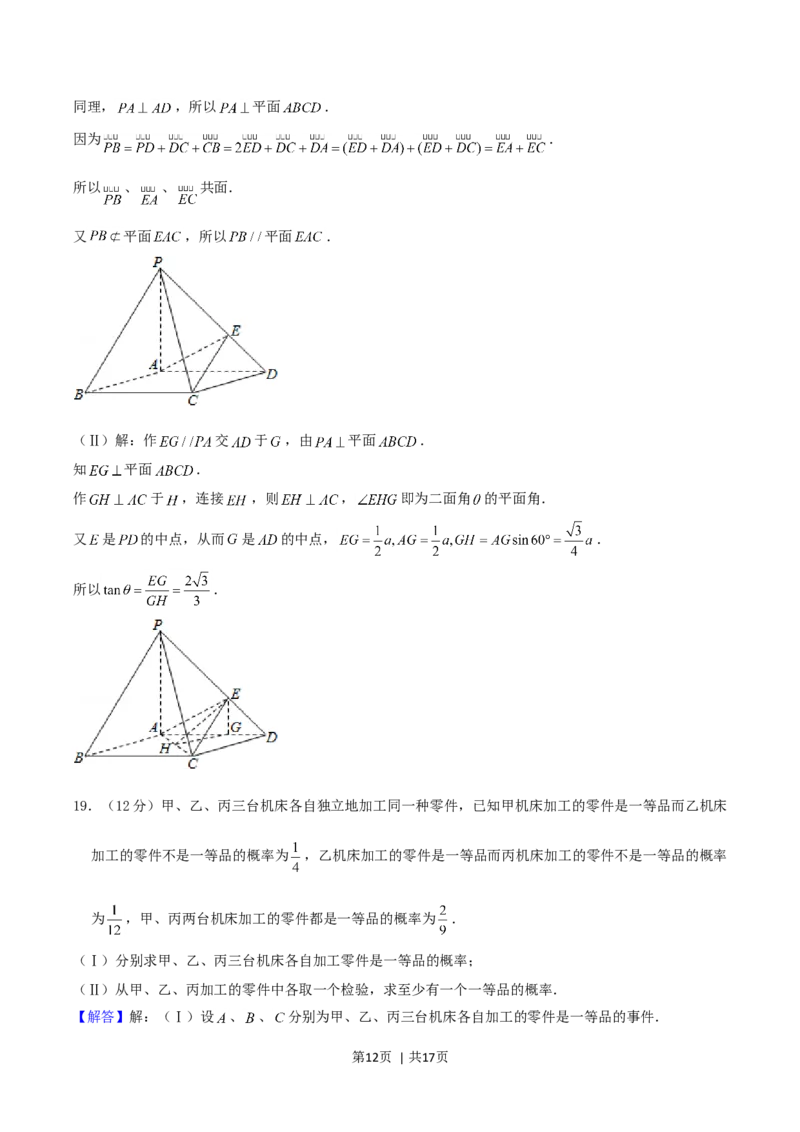
②:当 时,作出函数 图象:
若直线 与函数 且 的图象有两个公共点
由图象可知 ,
此时无解.
综上: 的取值范围是 .
故答案为:
第10页 | 共17页三、解答题(共6小题,满分74分)
17.(12分)已知 ,求 的值.
【解答】解:由 ,得 .
于是 .
18.(12分)如图,在底面是菱形的四棱锥 中, , , ,
点 是 的中点.
证明 平面 , 平面 ;
求以 为棱, 与 为面的二面角 的正切值.
【解答】(Ⅰ)证明:因为底面 是菱形, ,
所以 ,
在 中,由 知 .
第11页 | 共17页同理, ,所以 平面 .
因为 .
所以 、 、 共面.
又 平面 ,所以 平面 .
(Ⅱ)解:作 交 于 ,由 平面 .
知 平面 .
作 于 ,连接 ,则 , 即为二面角 的平面角.
又 是 的中点,从而 是 的中点, .
所以 .
19.(12分)甲、乙、丙三台机床各自独立地加工同一种零件,已知甲机床加工的零件是一等品而乙机床
加工的零件不是一等品的概率为 ,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率
为 ,甲、丙两台机床加工的零件都是一等品的概率为 .
(Ⅰ)分别求甲、乙、丙三台机床各自加工零件是一等品的概率;
(Ⅱ)从甲、乙、丙加工的零件中各取一个检验,求至少有一个一等品的概率.
【解答】解:(Ⅰ)设 、 、 分别为甲、乙、丙三台机床各自加工的零件是一等品的事件.
第12页 | 共17页由题设条件有
即
由①、③得
代入②得 (C) (C) .
解得 (C) 或 (舍去).
将 分别代入③、②可得
.
即甲、乙、丙三台机床各加工的零件是一等品的概率分别是 .
(Ⅱ)记 为从甲、乙、丙加工的零件中各取一个检验,至少有一个一等品的事件,
则 .
故从甲、乙、丙加工的零件中各取一个检验,至少有一个一等品的概率为 .
20.(12分)已知数列 是首项为 且公比 不等于1的等比数列, 是其前 项的和, , ,
成等差数列.
证明 , , 成等比数列;
求和 .
【解答】(Ⅰ)证明:由 , , 成等差数列,得 ,
第13页 | 共17页即 .
变形得 ,
又 公比 不等于1,所以
由 . .
得 .
所以 , , 成等比数列.
(Ⅱ)解: .
即 .①
① 得: ②.
① ②得 .
所以 .
21.(12 分)如图,已知曲线 与曲线 交于 , ,直线
与曲线 , 分别交于 , .
(Ⅰ)写出四边形 的面积 与 的函数关系式 ;
(Ⅱ)讨论 的单调性,并求 的最大值.
第14页 | 共17页【 解 答 】 解 : ( Ⅰ ) 由 得 交 点 、 的 坐 标 分 别 是 , ,
,
即 .
(Ⅱ) .令 解得 .
当 ,从而 在区间 上是增函数;
当 ,从而 在区间 上是减函数.
所以当 时, 有最大值为 .
22.(14分)如图,过抛物线 的对称轴上任一点 , 作直线与抛物线交于 , 两点,
点 是点 关于原点的对称点.
设点 分有向线段 所成的比为 ,证明:
(Ⅱ)设直线 的方程是 ,过 , 两点的圆 与抛物线在点 处有共同的切线,求圆
的方程.
第15页 | 共17页【解答】解:(Ⅰ)依题意,可设直线 的方程为 ,代入抛物线方程 得
.①
设 、 两点的坐标分别是 , 、 , ,则 、 是方程①的两根.
所以 .
由点 分有向线段 所成的比为 ,
得 .
又点 是点 关于原点的对称点,
故 点 的 坐 标 是 , 从 而
.
.
所以 .
(Ⅱ)由 得点 、 的坐标分别是 、 .
由 得 ,
所以抛物线 在点 处切线的斜率为
设圆 的方程是 ,
第16页 | 共17页则
解之得 .
所以圆 的方程是 ,
即 .
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布
日期:2019/5/23 23:08:29;用户:15217760367;邮箱:15217760367;学号:10888156
第17页 | 共17页