文档内容
2023—2024 学年高三(上)期中考试数学试卷
数 学
一、单选题
1. 已知集合 ,则 的真子集共有( )
A. 2个 B. 3个 C. 4个 D. 8个
【答案】B
【解析】
【分析】根据交集运算得集合P,再根据集合P中的元素个数,确定其真子集个数即可.
【详解】解:
, 的真子集是 共3个.
故选:B.
2. 若函数 在 上是减函数,则实数m的取值范围是( )
A. B. C. D.
【答案】B
【解析】
【分析】结合二次函数的对称轴和单调性求得 的取值范围.
【详解】函数 的对称轴为 ,
由于 在 上是减函数,所以 .
故选:B
3. 若“ ”是“ ”的充分不必要条件,则实数a的取值范围是( )
A. B.
C. D.
第1页/共18页
学科网(北京)股份有限公司【答案】B
【解析】
【分析】根据分式的性质、解一元二次不等式的方法、解绝对值不等式的公式法,结合充分不必要条件的
性质进行求解即可.
【详解】因为 ,则 ,
因为 ,则 ,
即 是 的充分而不必要条件,
所以 ,
故选:B
4. 已知焦距为4的双曲线 的一条渐近线与直线 垂直,则该双曲线的
方程为( )
A. B.
C. D.
【答案】C
【解析】
【分析】由已知焦距为4,得出 ,又由双曲线方程求出渐近线方程,而直线与渐近线垂直,
得出它们斜率之积为 ,从而得出 、 之间的关系,代入 ,解出 、 ,写出方程即
可.
【详解】由已知焦距为4,所以 , ,又双曲线方程的渐近线方程为: ,而
第2页/共18页
学科网(北京)股份有限公司直线的斜率 ,且直线与一条渐近线垂直,所以 ,即 ,由
解得 ,所以双曲线方程为:
故选:C.
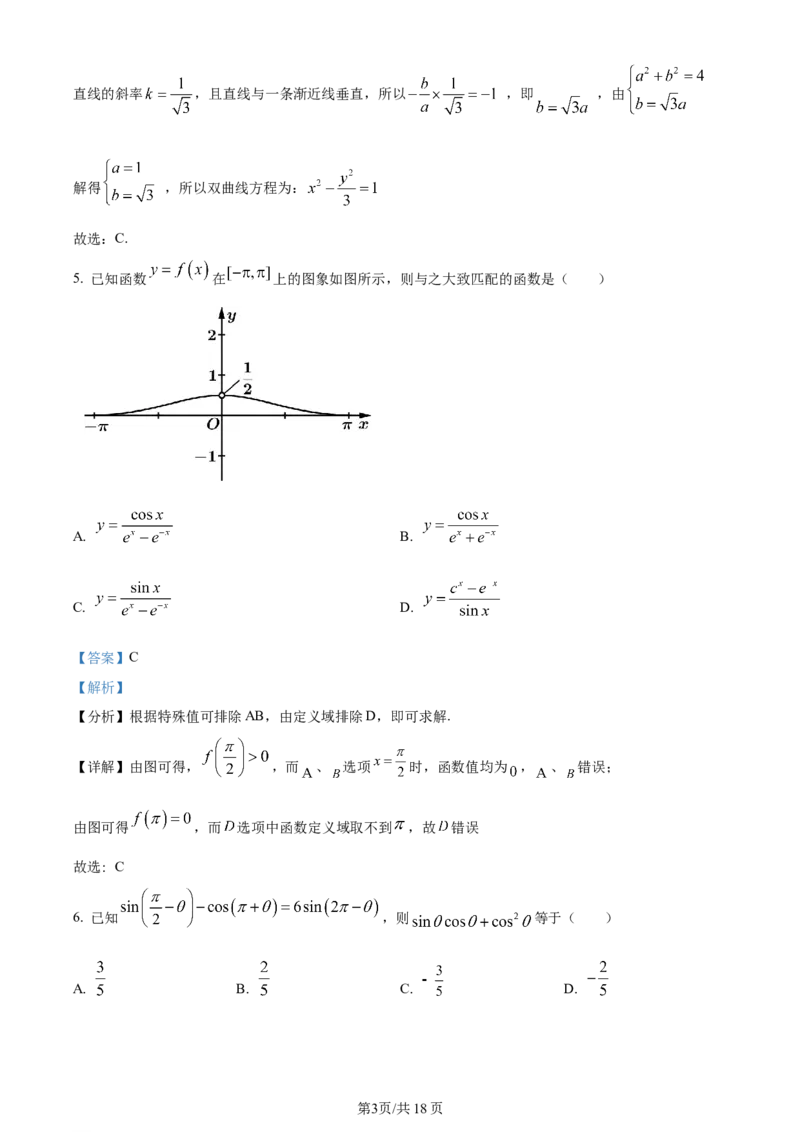
5. 已知函数 在 上的图象如图所示,则与之大致匹配的函数是( )
A. B.
C. D.
【答案】C
【解析】
【分析】根据特殊值可排除AB,由定义域排除D,即可求解.
【详解】由图可得, ,而 、 选项 时,函数值均为 , 、 错误;
.
由图可得 ,而 选项中函数定义域取不到 ,故 错误
故选: C
6. 已知 ,则 等于( )
A. B. C. D.
第3页/共18页
学科网(北京)股份有限公司【答案】A
【解析】
【分析】
利用诱导公式化简整理,可求得 的值,将所求改写成 ,上
下同除 ,即可得结果.
【详解】由题意得 ,所以 ,解得 ,
所以 .
故选:A
7. 设 , , ,则( )
A. B. C. D.
【答案】D
【解析】
【分析】构造 ,并利用导数、对数的性质研究大小关系即可.
【详解】设函数 ,则 ,
所以 为减函数,则 ,即 ,又 ,
所以 .
故选:D
8. 已知定义在 上的函数 满足,① ,② 为奇函数,③当 时,
恒成立.则 、 、 的大小关系正确的是( )
第4页/共18页
学科网(北京)股份有限公司A. B.
C. D.
【答案】A
【解析】
【分析】根据函数的奇偶性、周期性和单调性即可比较 的大小.
【详解】由 可得 的周期为 ,
因为 为奇函数,则 ,
又因为 的周期为 ,所以 ,即 为奇函数,
因为 时, ,所以 在 上单调递增,
因为 为奇函数,所以 在 上单调递增,所以 在 上单调递增,
因为 的周期为 , , ,
,所以 ,
即 .
故选:A.
二、多选题
9. 下列函数中,满足“ , ,都有 ”的有( )
A. B.
第5页/共18页
学科网(北京)股份有限公司C. D.
【答案】AD
【解析】
【分析】根据题意可知满足题意的函数为在 上减函数,由此一一判断选项中函数的单调性,可得
答案.
【详解】由 , ,都有 ,可知函数 在 时减函数.
函数 在 时为减函数,符合题意,故A正确;
函数 在 时为增函数,所以 在 时为增函数,故B
错误;
函数 图象的对称轴为 ,故在 时 为增函数,故C
错误;
函数 在 时单调递减,符合题意,故D正确.
故选:AD.
10. 已知复数 ,则下列说法正确的是( )
A. 复数 在复平面内对应的点在第四象限 B. 复数 的虚部为
C. 复数 的共轭复数 D. 复数 的模
【答案】BCD
【解析】
【分析】化简得 ,再得到其在复平面内对应的点的象限,虚部,共轭复数,模即可得到答案.
【详解】 ,
第6页/共18页
学科网(北京)股份有限公司,所以复数 在复平面内对应的点在第三象限,故A错误;
虚部为 ,故B正确;
复数 的共轭复数 ,故C正确;
复数 的模 ,故D正确;
故选:BCD.
11. 设函数 ,则下列结论正确的是( )
A. 的一个周期为 B. 的图象关于直线 对称
C. 的一个零点为 D. 在 上单调递减
【答案】ABC
【解析】
【分析】根据周期、对称轴、零点、单调性,结合整体思想即可求解.
【详解】对于A项,函数的周期为 , ,当 时,周期 ,故A项正确;
对于B项,当 时, 为最小值,此时 的
图象关于直线 对称,故B项正确;
对于C项, , ,所以 的一个零点为 ,
故C项正确;
对于D项,当 时, ,此时函数 有增有减,不是单调函数,故D项错误.
.
故选:ABC
12. 已知等差数列 的前n项和为 ,且满足 , ,则( )
第7页/共18页
学科网(北京)股份有限公司A. 数列 是递增数列 B. 数列 是递增数列
C. 的最小值是 D. 使得 取得最小正数的
【答案】AC
【解析】
【分析】根据题意,结合等差数列的性质以及前 项和的公式与性质,一一判断即可.
【详解】因为 , ,所以 ,可得公差 , 的最小值是 ,故AC
正确;
因为 , 单调递减, , 单调递增,所以B项错误;
因为 ,所以 ,
同理 ,所以 取得最小正数的 ,D项错误.
故选AC项.
三、填空题
13. 若 , ,则 ________________.
【答案】
【解析】
【分析】根据题意,利用三角函数的定义,准确运算,即可求解.
【详解】因为 ,且 ,
可令 ,则 ,设 终边上一点的坐标 ,
则 ,可得 .
故答案为: .
第8页/共18页
学科网(北京)股份有限公司14. 若直线 与曲线 相切,则 的值为___________.
【答案】
【解析】
【分析】设切点为 ,利用导数的几何意义结合条件即得.
【详解】设切点为 ,则 , ,
, ,
,
所以 , .
故答案为: .
15. 记函数 的最小正周期为T,若 , 为 的零
点,则 的最小值为____________.
【答案】
【解析】
【分析】首先表示出 ,根据 求出 ,再根据 为函数的零点,即可求出 的取值,从
而得解;
【详解】解: 因为 ,( , )
所以最小正周期 ,因为 ,
又 ,所以 ,即 ,
又 为 的零点,所以 ,解得 ,
第9页/共18页
学科网(北京)股份有限公司因为 ,所以当 时 ;
故答案为:
16. 已知函数 存在极值,则实数 的取值范围是___________.
【答案】
【解析】
【分析】分析可知函数 在 上存在极值点,求得 ,可得出
,即可求得实数 的取值范围.
【详解】函数 的定义域为 ,且 ,
由题意可知,函数 在 上存在极值点,
对于方程 , ,解得 或 ,
解方程 可得 , ,且 ,
故有 ,整理可得 .
若 ,则 ,矛盾;
若 ,则 .
综上所述,实数 的取值范围是 .
故答案为: .
第10页/共18页
学科网(北京)股份有限公司四、解答题
17. 在 中,a,b,c分别是角A、B、C的对边,且 .
(1)求C;
(2)若 ,求A.
【答案】(1)
(2)
【解析】
【分析】(1)由余弦定理即可求解,
(2)利用正弦定理边角互化,结合两角和的正弦公式即可得 ,进而可求解.
【小问1详解】
∵ ,∴ ,∴ ,
由于C是三角形内角,∴ .
【小问2详解】
由正弦定理可得 ,
∴
∴ ,∴ ,
∴ ,∴ .
∵ ,∴ ,
由于B是三角形内角 ,∴ ,则 .
18. 设各项非负的数列 的前 项和为 ,已知 ,且 成等比数列.
第11页/共18页
学科网(北京)股份有限公司(1)求 的通项公式;
(2)若 ,数列 的前 项和 .
【答案】(1)
(2)
【解析】
【分析】(1)利用 得出 的递推关系,从而得数列从第2项起为等差数列,结合
等比数列的性质可求得 ,这样可得通项公式 ,然后由已知式中令 求得 ,比较后可得结
论;
(2)用错位相减法求和.
【小问1详解】
当 时, ,
当 时, ①, ②.
①-②得 ,即 ,
∵ ,∴ ,
∴数列 从第2项起是公差为1的等差数列.
∴ ,
又 , , 成等比数列,∴ ,即 ,
解得 ,∴ ,
∵ ,∴ ,适合上式,
∴数列 的通项公式为 .
第12页/共18页
学科网(北京)股份有限公司【小问2详解】
,
∴数列 的前 项的和为
③
④
③-④得
,
∴ .
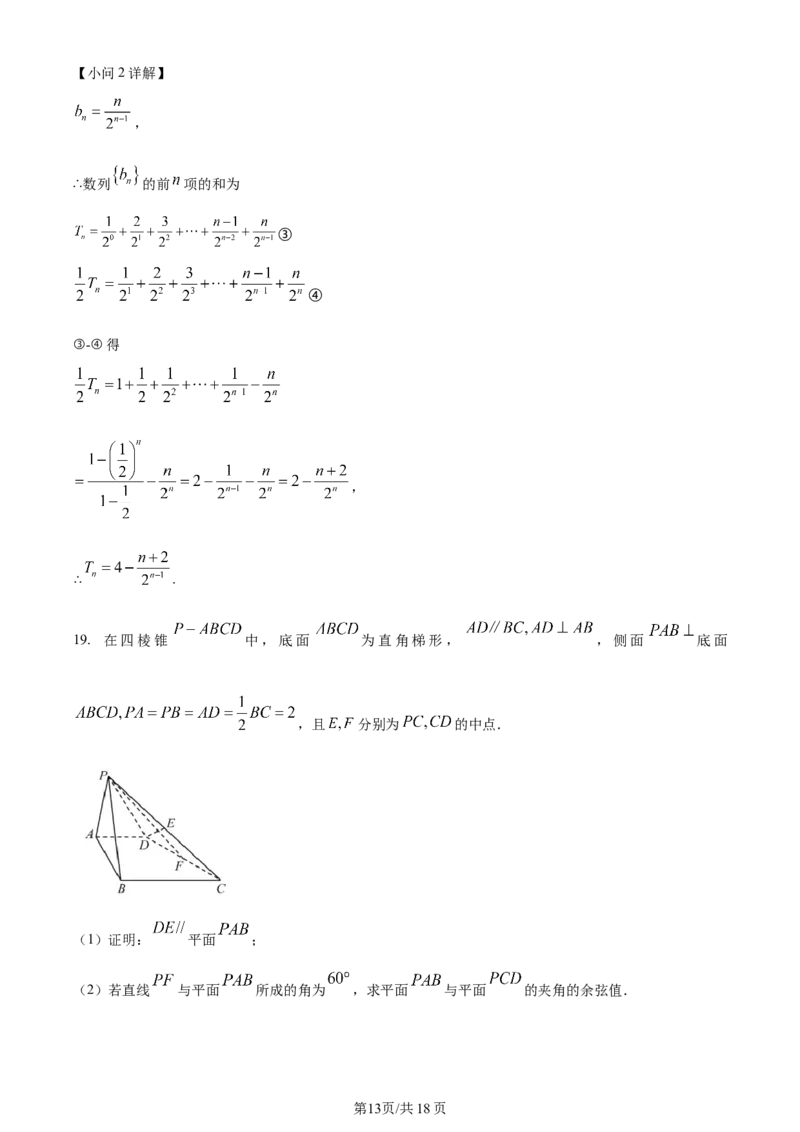
19. 在四棱锥 中,底面 为直角梯形, ,侧面 底面
,且 分别为 的中点.
(1)证明: 平面 ;
(2)若直线 与平面 所成的角为 ,求平面 与平面 的夹角的余弦值.
第13页/共18页
学科网(北京)股份有限公司【答案】(1)证明见解析
(2)
【解析】
【分析】(1)取 中点 ,连接 ,通过证明四边形 为平行四边形,即可证明结论;
(2)由直线 与平面 所成的角为 ,可得 ,建立以G为原点的空间直角
坐标系,利用向量方法可得答案.
【小问1详解】
证明:取 中点 ,连接 ,
为 的中点,
,又 ,
,
四边形 为平行四边形:
,
平面 平面 ,
平面 ;
【小问2详解】
平面 平面 ,平面 平面 平面 , 平面
,
取 中点 ,连接 ,则 平面 ,
,
第14页/共18页
学科网(北京)股份有限公司,又 ,
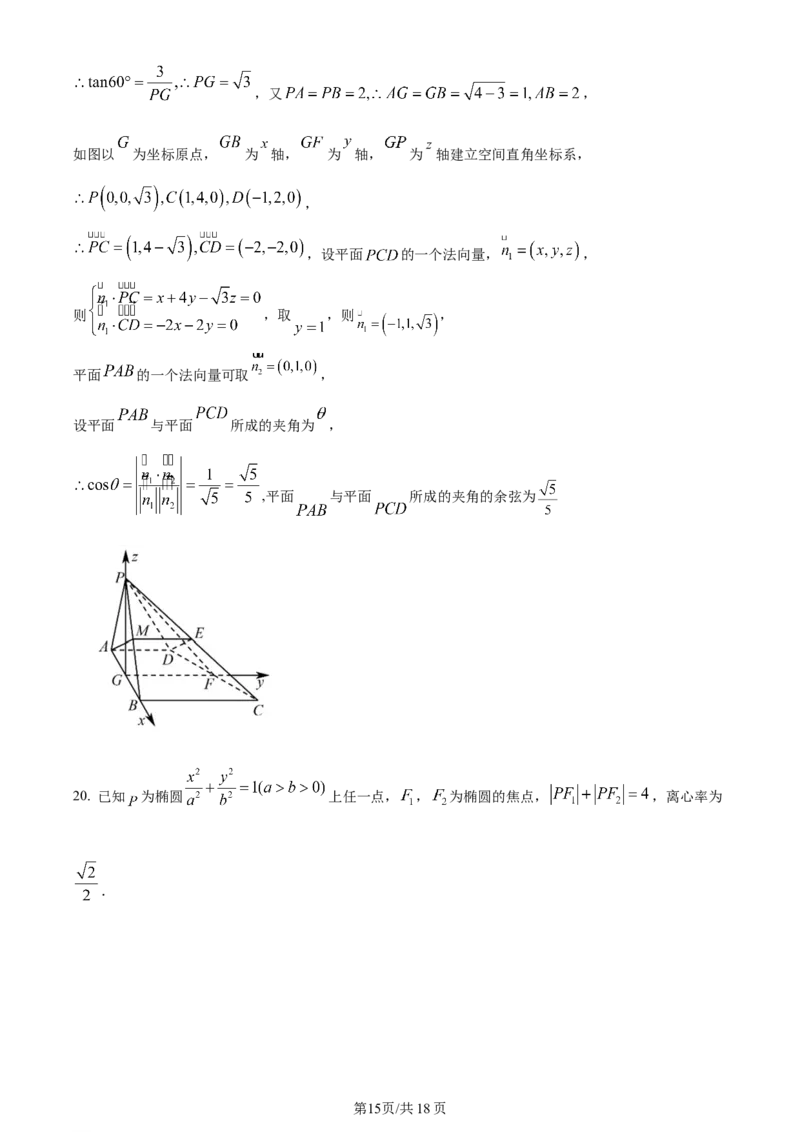
如图以 为坐标原点, 为 轴, 为 轴, 为 轴建立空间直角坐标系,
,
,设平面 的一个法向量, ,
则 ,取 ,则 ,
平面 的一个法向量可取 ,
设平面 与平面 所成的夹角为 ,
,平面 与平面 所成的夹角的余弦为
20. 已知 为椭圆 上任一点, , 为椭圆的焦点, ,离心率为
.
第15页/共18页
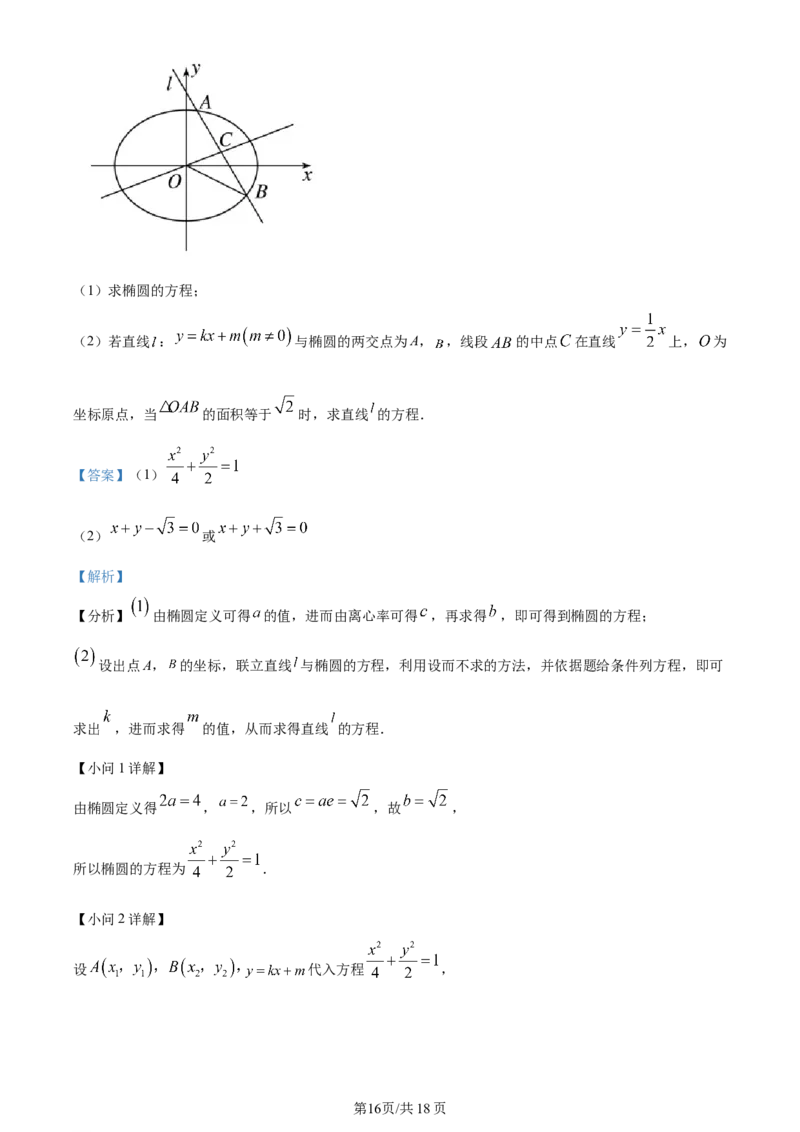
学科网(北京)股份有限公司(1)求椭圆的方程;
(2)若直线 : 与椭圆的两交点为A, ,线段 的中点 在直线 上, 为
坐标原点,当 的面积等于 时,求直线 的方程.
【答案】(1)
(2) 或
【解析】
【分析】 由椭圆定义可得 的值,进而由离心率可得 ,再求得 ,即可得到椭圆的方程;
设出点A, 的坐标,联立直线 与椭圆的方程,利用设而不求的方法,并依据题给条件列方程,即可
求出 ,进而求得 的值,从而求得直线 的方程.
【小问1详解】
由椭圆定义得 , ,所以 ,故 ,
所以椭圆的方程为 .
【小问2详解】
设 代入方程 ,
第16页/共18页
学科网(北京)股份有限公司得
所以 , ,
所以 ,解得 ,
则 式变为 则 ,
底边 上的高 ,所以 的面积 .
令 ,解得 ,
把 , 代入 式,经检验,均满足 ,
此时直线 的方程为 或 .
21. 学校团委和工会联合组织教职员工进行益智健身活动比赛.经多轮比赛后,由教师甲、乙作为代表进行
决赛.决赛共设三个项目,每个项目胜者得10分,负者得 分,没有平局.三个项目比赛结束后,总得分高
的获得冠军.已知教师甲在三个项目中获胜的概率分别为0.4,0.5,0.75,各项目的比赛结果相互独立.甲、
乙获得冠军的概率分别记为 , .
(1)判断甲、乙获得冠军的实力是否有明显差别(如果 ,那么认为甲、乙
获得冠军的实力有明显差别,否则认为没有明显差别);
(2)用X表示教师乙的总得分,求X的分布列与期望.
【答案】(1)甲、乙获得冠军的实力没有明显差别
(2)分布列见解析,
【解析】
第17页/共18页
学科网(北京)股份有限公司【分析】(1)设教师甲在三个项目中获胜的事件依次为 ,利用互斥事件和独立事件的概率共求得
和 ,结合 ,即可得到结论;
(2)根据题意,得到 的可能取值为 ,利用独立事件的概率乘法公式,求得相应的概率,得
出分布列,结合期望的公式,即可求解.
【小问1详解】
解:设教师甲在三个项目中获胜的事件依次为 ,
则教师甲获得冠军的概率
,
由对立事件的概率公式,可得得 ,
所以 ,解得 ,
因为 ,所以甲、乙获得冠军 实力没有明显差别.
的
【小问2详解】
解:根据题意知, 的可能取值为 ,
可得 ,
,
,
.
所以随机变量 的分布列为
第18页/共18页
学科网(北京)股份有限公司0 15 30
0.15 0.425 0.35 0.075
所以期望为 .
22. 已知函数 .
(1)若不等式 在区间 内恒成立,求实数 的取值范围;
(2)求证: ( 为自然对数的底数)
【答案】(1)
(2)证明见解析
【解析】
【分析】(1)分离参数,转化为求定函数的最值问题;
(2)根据第一问,合理构造,利用不等式的性质合理变形达到证明的目的.
【小问1详解】
因为 , ,所以 ,
令 ,又 ,令 解得 ,
时, , 递增, 时, , 递减,
所以当 时函数 有最大值,且最大值为 ,所以 .
【小问2详解】
由(1)知 ,所以 ,
所以
第19页/共18页
学科网(北京)股份有限公司,
又
,
所以 ,
即 .
第20页/共18页
学科网(北京)股份有限公司