2004年福建高考文科数学真题及答案_数学高考真题试卷_旧1990-2007·高考数学真题_1990-2007·高考数学真题·PDF_福建

2004 年福建高考文科数学真题及答案 一、选择题（共12小题，每小题5分，满分60分） 1．（5分）已知全集U {1，2，3，4，5}，A{1，2，3}，B{3，4}，则ð (A B)( ) U  A．{3} B．{5} C．{1，2，4，5} D．{1，2，3，4} 2．（5分）tan15cot15等于( ) 4 3 A．2 B．2 3 C．4 D． 3 3．（5 分）命题 p：若 a、 bR，则|a||b|1是|ab|1的充分而不必要条件；命题 q：函数 y |x1|2的定义域是(，1] [3，)，则( )  A．“ p或q”为假 B．“ p且q”为真 C． p真q假 D． p假q真 4．（5分）已知F ，F 是椭圆的两个焦点，过F 且与椭圆长轴垂直的直线交椭圆于A，B两点，若ABF 1 2 1 2 是正三角形，则这个椭圆的离心率是( ) 2 2 3 3 A． B． C． D． 2 3 3 2 a 5 S 5．（5分）设S 是等差数列{a }的前n项和，若 5  ,则 9 ( ) n n a 9 S 3 5 1 A．1 B．1 C．2 D． 2 6．（5分）已知m、n是不重合的直线，、是不重合的平面，有下列命题： ①若m，n//，则m//n； ②若m//，m//，则//； ③若 n，m//n，则m//且m//；  ④若m，m，则//． 其中真命题的个数是( ) A．0 B．1 C．2 D．3 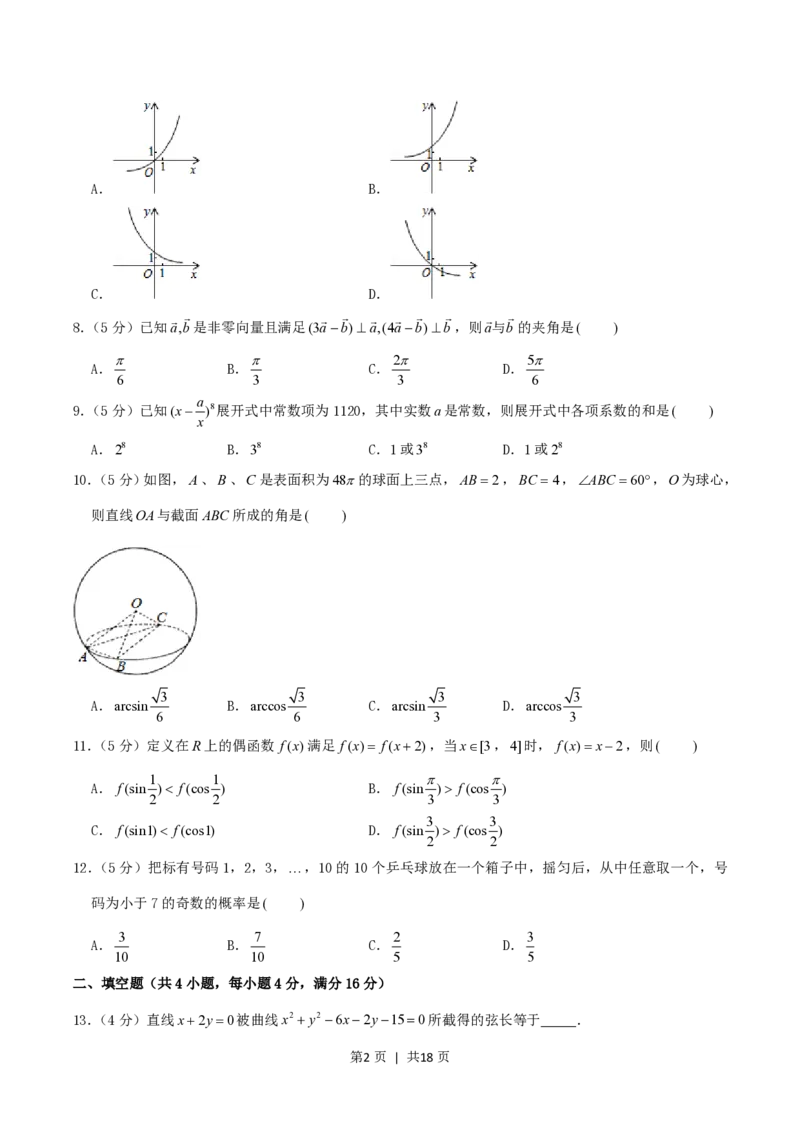7．（5分）已知函数ylog x的反函数是y f1(x)，则函数y f1(1x)的图象是( ) 2 第1页 | 共18页A． B． C． D． 8．（5分）已知a,b  是非零向量且满足(3ab  )a,(4ab  )b  ，则a与b  的夹角是( )   2 5 A． B． C． D． 6 3 3 6 a 9．（5分）已知(x )8展开式中常数项为1120，其中实数a是常数，则展开式中各项系数的和是( ) x A．28 B．38 C．1或38 D．1或28 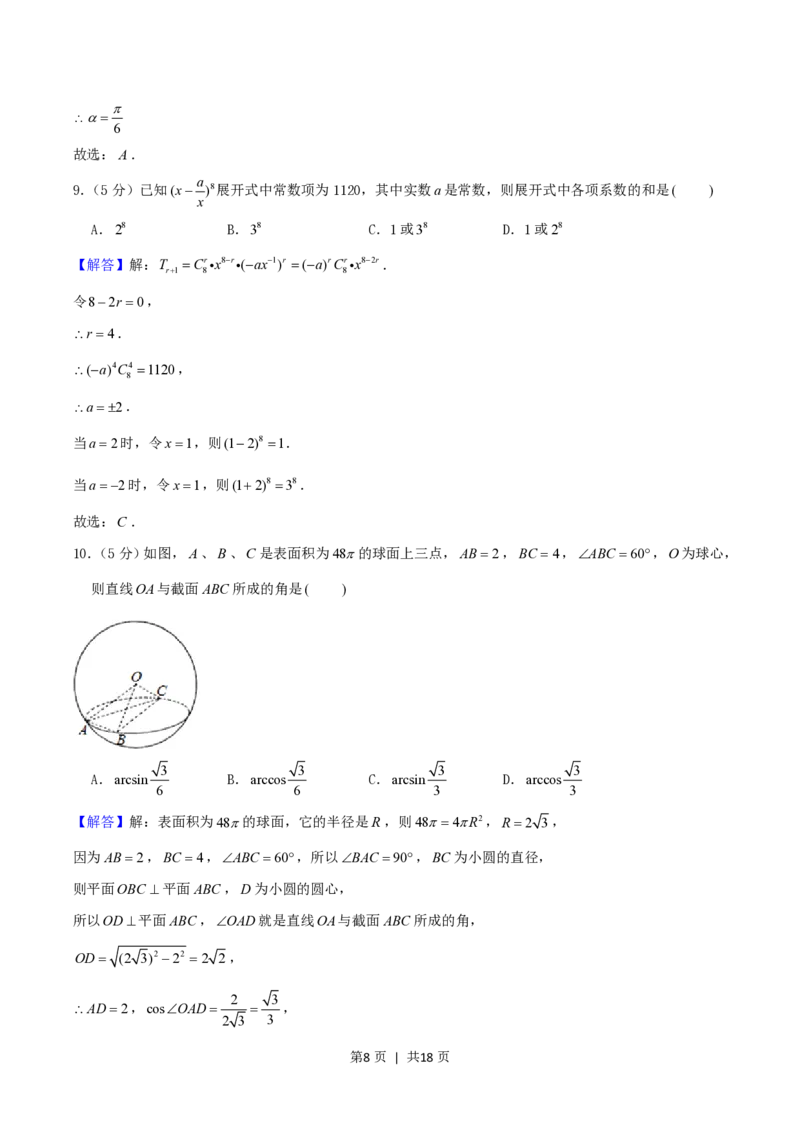10．（5分）如图，A、B、C是表面积为48的球面上三点，AB2，BC 4，ABC 60，O为球心， 则直线OA与截面ABC所成的角是( ) 3 3 3 3 A．arcsin B．arccos C．arcsin D．arccos 6 6 3 3 11．（5分）定义在R上的偶函数 f(x)满足 f(x) f(x2)，当x[3，4]时， f(x)x2，则( ) 1 1   A． f(sin ) f(cos ) B． f(sin ) f(cos ) 2 2 3 3 3 3 C． f(sin1) f(cos1) D． f(sin ) f(cos ) 2 2 12．（5分）把标有号码1，2，3，，10的10个乒乓球放在一个箱子中，摇匀后，从中任意取一个，号 码为小于7的奇数的概率是( ) 3 7 2 3 A． B． C． D． 10 10 5 5 二、填空题（共4小题，每小题4分，满分16分） 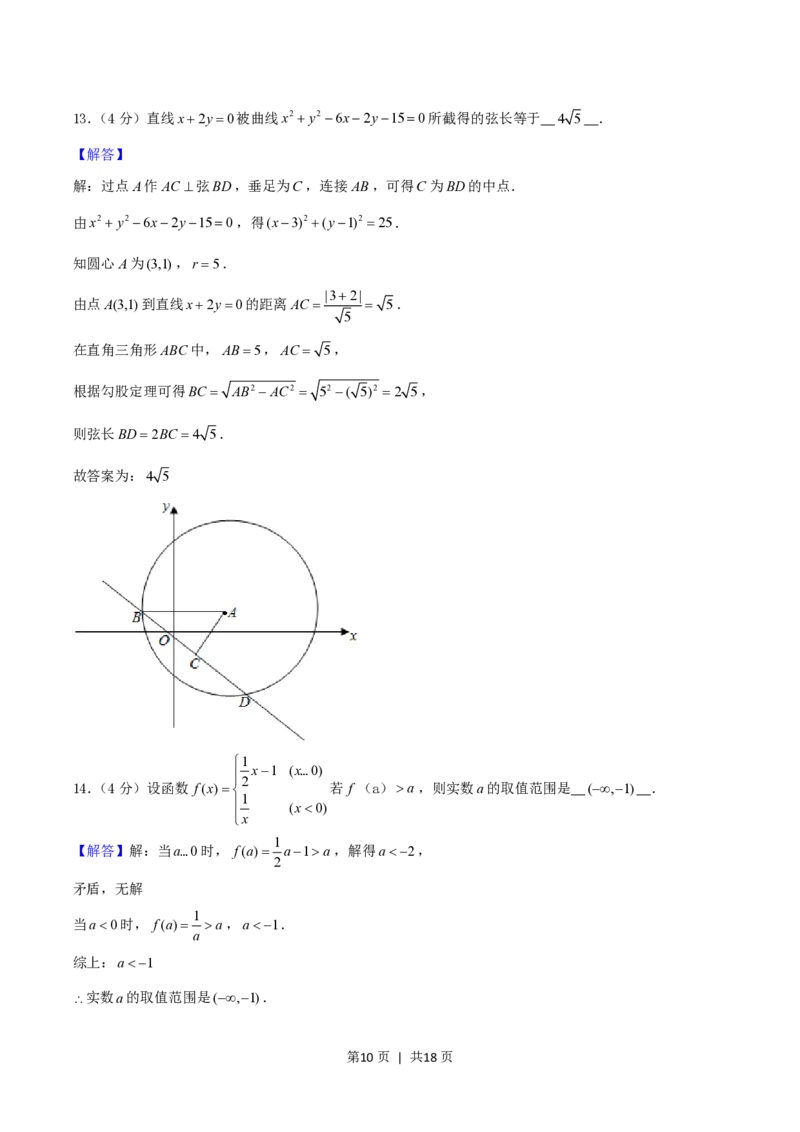13．（4分）直线x2y0被曲线x2  y2 6x2y150所截得的弦长等于 ． 第2页 | 共18页1 x1 (x…0)  2 14．（4分）设函数 f(x) 若 f （a）a，则实数a的取值范围是 ． 1  (x0) x 15．（4分）一个总体中有100个个体，随机编号为0，1，2，，99，依编号顺序平均分成10个小组，组 号依次为1，2，3，，10．现用系统抽样方法抽取一个容量为10的样本，规定如果在第1组随机抽取 的号码为m，那么在第k小组中抽取的号码个位数字与mk的个位数字相同．若m6，则在第7组中 抽取的号码是 ． 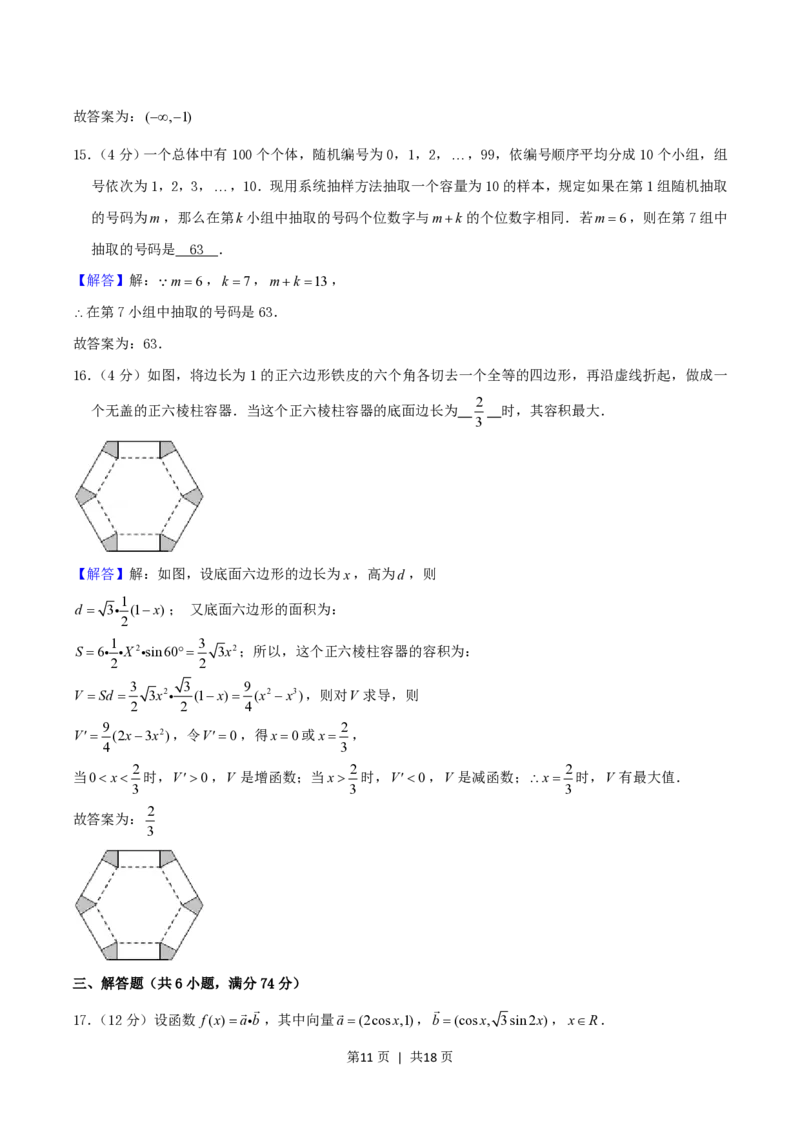16．（4分）如图，将边长为1的正六边形铁皮的六个角各切去一个全等的四边形，再沿虚线折起，做成一 个无盖的正六棱柱容器．当这个正六棱柱容器的底面边长为 时，其容积最大． 三、解答题（共6小题，满分74分） 17．（12分）设函数 f(x)a b  ，其中向量a(2cosx,1)，b  (cosx, 3sin2x)，xR．    （1）若 f(x)1 3，且x[ ， ]，求x； 3 3  （2）若函数y2sin2x的图象按向量c(m,n)，(|m| )平移后得到函数y f(x)的图象，求实数m、n 2 的值． 18．（12分）甲、乙两人同时参加奥运志愿者选拔赛的考试，已知在备选的10道题中，甲能答对其中的6 道题，乙能答对其中的8道题．规定每次考试都从备选题中随机抽出3道题进行测试，至少答对2道题 才能入选． (I)求甲答对试题数的分布列及数学期望； (II)求甲、乙两人至少有一人入选的概率． 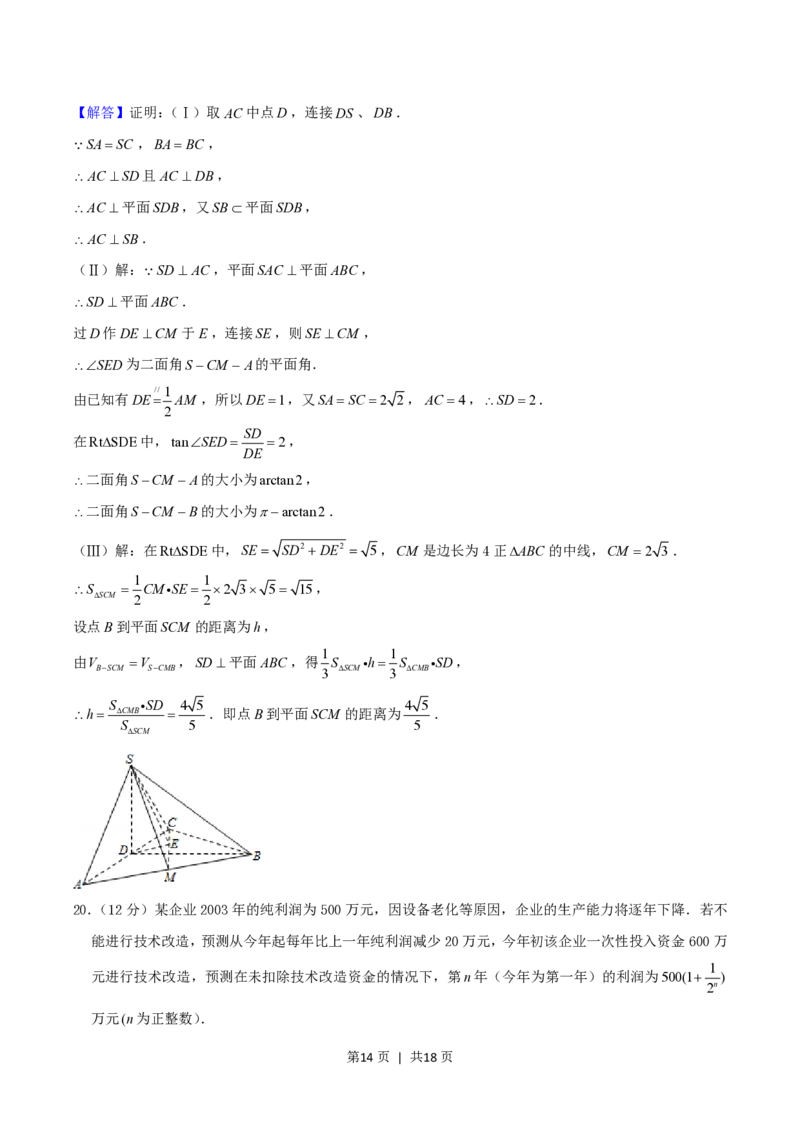19．（12 分）在三棱锥 SABC中， ABC 是边长为 4 的正三角形，平面 SAC 平面 ABC， SASC 2 2，M 为AB的中点． （Ⅰ）证明：AC SB； （Ⅱ）求二面角SCM B的大小； （Ⅲ）求点B到平面SCM 的距离． 第3页 | 共18页20．（12分）某企业2003年的纯利润为500万元，因设备老化等原因，企业的生产能力将逐年下降．若不 能进行技术改造，预测从今年起每年比上一年纯利润减少20万元，今年初该企业一次性投入资金600万 1 元进行技术改造，预测在未扣除技术改造资金的情况下，第n年（今年为第一年）的利润为500(1 ) 2n 万元(n为正整数）． （Ⅰ）设从今年起的前n年，若该企业不进行技术改造的累计纯利润为A 万元，进行技术改造后的累计纯 n 利润为B 万元（须扣除技术改造资金），求A 、B 的表达式； n n n （Ⅱ）依上述预测，从今年起该企业至少经过多少年，进行技术改造后的累计纯利润超过不进行技术改造 的累计纯利润？ 1 21．（12分）如图，P是抛物线C:y x2上一点，直线l过点P并与抛物线C在点P的切线垂直，l与抛 2 物线C相交于另一点Q． （Ⅰ）当点P的横坐标为2时，求直线l的方程； （Ⅱ）当点P在抛物线C上移动时，求线段PQ中点M 的轨迹方程，并求点M 到x轴的最短距离． 2 22．（14分）已知 f(x)4xax2  x3(xR)在区间[1，1]上是增函数． 3 （Ⅰ）求实数a的值组成的集合A； 1 （Ⅱ）设关于x的方程 f(x)2x x3的两个非零实根为x 、x ．试问：是否存在实数m，使得不等式 3 1 2 m2 tm1… |x x |对任意aA及t[1，1]恒成立？若存在，求m的取值范围；若不存在，请说明理 1 2 由． 第4页 | 共18页2004年福建省高考数学试卷（文科） 参考答案与试题解析 一、选择题（共12小题，每小题5分，满分60分） 1．（5分）已知全集U {1，2，3，4，5}，A{1，2，3}，B{3，4}，则ð (A B)( ) U  A．{3} B．{5} C．{1，2，4，5} D．{1，2，3，4} 【解答】解： 全集U {1，2，3，4，5}，A{1，2，3}，B{3，4}，  A B{1，2，3，4}，  ð (A B){5}， U  故选：B． 2．（5分）tan15cot15等于( ) 4 3 A．2 B．2 3 C．4 D． 3 sin15 cos15 sin215cos215 1 【解答】解：解法1:tan15cot15    4． cos15 sin15 cos15sin15 1 sin30  2 3 1 tan45tan30 3 3 3 解法2：由tan15tan(4530)   ． 1tan45tan30 3 3 3 1 3 3 3 3 3 原式  4． 3 3 3 3 故选：C． 3．（5 分）命题 p：若 a、 bR，则|a||b|1是|ab|1的充分而不必要条件；命题 q：函数 y |x1|2的定义域是(，1] [3，)，则( )  A．“ p或q”为假 B．“ p且q”为真 C． p真q假 D． p假q真 【解答】解： |ab|„ |a||b|，  若|a||b|1，不能推出|ab|1，而|ab|1，一定有|a||b|1，故命题 p为假． 又由函数y |x1|2的定义域为|x1|2…0，即|x1|…2，即x1…2或x1„ 2． 第5页 | 共18页故有x(，1] [3，)．  q为真命题． 故选：D． 4．（5分）已知F ，F 是椭圆的两个焦点，过F 且与椭圆长轴垂直的直线交椭圆于A，B两点，若ABF 1 2 1 2 是正三角形，则这个椭圆的离心率是( ) 2 2 3 3 A． B． C． D． 2 3 3 2 3 b2 3 2 3 【解答】解：由题|AF | |FF |，  2c即a2 c2  ac 1 3 1 2 a 3  3 2 3 c2  aca2 0， 3 2 3 e2  e10， 3 3 解之得：e （负值舍去）． 3 故选：C． a 5 S 5．（5分）设S 是等差数列{a }的前n项和，若 5  ,则 9 ( ) n n a 9 S 3 5 1 A．1 B．1 C．2 D． 2 【解答】解：设等差数列{a }的首项为a ，由等差数列的性质可得 n 1 a a 2a ，a a 2a ， 1 9 5 1 5 3 a a 1 9 9 s 2 9a 9 5  9   5   1， s a a 5a 5 9 5 1 5 5 3 2 故选：A． 6．（5分）已知m、n是不重合的直线，、是不重合的平面，有下列命题： ①若m，n//，则m//n； ②若m//，m//，则//； ③若 n，m//n，则m//且m//；  ④若m，m，则//． 第6页 | 共18页其中真命题的个数是( ) A．0 B．1 C．2 D．3 【解答】解：①若m，n//，则m与n平行或异面，故不正确； ②若m//，m//，则与可能相交或平行，故不正确； ③若 n，m//n，则m//且m//，m也可能在平面内，故不正确；  ④若m，m，则//，垂直与同一直线的两平面平行，故正确 故选：B． 7．（5分）已知函数ylog x的反函数是y f1(x)，则函数y f1(1x)的图象是( ) 2 A． B． C． D． 【解答】解： ylog x x2y  f1(x)2x  f1(1x)21x．函数y f1(1x)的图象是C．  2 故选：C． 8．（5分）已知a,b  是非零向量且满足(3ab  )a,(4ab  )b  ，则a与b  的夹角是( )   2 5 A． B． C． D． 6 3 3 6 【解答】解：设a与b  的夹角是 (3ab  )a,(4ab  )b   (3ab  ) a0,(4ab  ) b  0   即3a2 ab  0;4ab  b  2 0 a b  3a2;b  2 12a2  a b  3a2 3 cos    |a||b  | 2 3a2 2 第7页 | 共18页  6 故选：A． a 9．（5分）已知(x )8展开式中常数项为1120，其中实数a是常数，则展开式中各项系数的和是( ) x A．28 B．38 C．1或38 D．1或28 【解答】解：T Cr x8r (ax1)r (a)rCr x82r． r1 8  8 令82r 0， r 4． (a)4C4 1120， 8 a2． 当a2时，令x1，则(12)8 1． 当a2时，令x1，则(12)8 38． 故选：C． 10．（5分）如图，A、B、C是表面积为48的球面上三点，AB2，BC 4，ABC 60，O为球心， 则直线OA与截面ABC所成的角是( ) 3 3 3 3 A．arcsin B．arccos C．arcsin D．arccos 6 6 3 3 【解答】解：表面积为48的球面，它的半径是R，则484R2，R2 3， 因为AB2，BC 4，ABC 60，所以BAC 90，BC为小圆的直径， 则平面OBC 平面ABC，D为小圆的圆心， 所以OD平面ABC，OAD就是直线OA与截面ABC所成的角， OD (2 3)2 22 2 2， 2 3 AD2，cosOAD  ， 2 3 3 第8页 | 共18页故选：D． 11．（5分）定义在R上的偶函数 f(x)满足 f(x) f(x2)，当x[3，4]时， f(x)x2，则( ) 1 1   A． f(sin ) f(cos ) B． f(sin ) f(cos ) 2 2 3 3 3 3 C． f(sin1) f(cos1) D． f(sin ) f(cos ) 2 2 【解答】解：x[3，4]时， f(x)x2，故偶函数 f(x)在[3，4]上是增函数， 又定义在R上的偶函数 f(x)满足 f(x) f(x2)，故函数的周期是2 所以偶函数 f(x)在(1,0)上是增函数， 所以 f(x)在(0,1)上是减函数， 1 1 观察四个选项A中sin cos ，故A不对； 2 2   B选项中sin cos ，故B不对； 3 3 C选项中sin1cos1，故C对； D亦不对． 综上，选项C是正确的． 故选：C． 12．（5分）把标有号码1，2，3，，10的10个乒乓球放在一个箱子中，摇匀后，从中任意取一个，号 码为小于7的奇数的概率是( ) 3 7 2 3 A． B． C． D． 10 10 5 5 【解答】解：因为所有机会均等的可能共有10种，而号码小于7的奇数有1，3，5共3种， 3 所以抽到号码为小于7的奇数的概率是 ． 10 故选：A． 二、填空题（共4小题，每小题4分，满分16分） 第9页 | 共18页13．（4分）直线x2y0被曲线x2  y2 6x2y150所截得的弦长等于 4 5 ． 【解答】 解：过点A作AC 弦BD，垂足为C，连接AB，可得C为BD的中点． 由x2  y2 6x2y150，得(x3)2 (y1)2 25． 知圆心A为(3,1)，r 5． |32| 由点A(3,1)到直线x2y0的距离AC   5． 5 在直角三角形ABC中，AB5，AC  5， 根据勾股定理可得BC  AB2 AC2  52 ( 5)2 2 5， 则弦长BD2BC 4 5． 故答案为：4 5 1 x1 (x…0)  2 14．（4分）设函数 f(x) 若 f （a）a，则实数a的取值范围是 (,1) ． 1  (x0) x 1 【解答】解：当a…0时， f(a) a1a，解得a2， 2 矛盾，无解 1 当a0时， f(a) a，a1． a 综上：a1 实数a的取值范围是(,1)． 第10页 | 共18页故答案为：(,1) 15．（4分）一个总体中有100个个体，随机编号为0，1，2，，99，依编号顺序平均分成10个小组，组 号依次为1，2，3，，10．现用系统抽样方法抽取一个容量为10的样本，规定如果在第1组随机抽取 的号码为m，那么在第k小组中抽取的号码个位数字与mk的个位数字相同．若m6，则在第7组中 抽取的号码是 63 ． 【解答】解： m6，k 7，mk 13，  在第7小组中抽取的号码是63． 故答案为：63． 16．（4分）如图，将边长为1的正六边形铁皮的六个角各切去一个全等的四边形，再沿虚线折起，做成一 2 个无盖的正六棱柱容器．当这个正六棱柱容器的底面边长为 时，其容积最大． 3 【解答】解：如图，设底面六边形的边长为x，高为d，则 1 d  3 (1x)； 又底面六边形的面积为：  2 1 3 S 6 X2 sin60 3x2；所以，这个正六棱柱容器的容积为：    2 2 3 3 9 V Sd  3x2 (1x) (x2 x3)，则对V 求导，则  2 2 4 9 2 V (2x3x2)，令V0，得x0或x ， 4 3 2 2 2 当0x 时，V0，V 是增函数；当x 时，V0，V 是减函数；x 时，V 有最大值． 3 3 3 2 故答案为： 3 三、解答题（共6小题，满分74分） 17．（12分）设函数 f(x)a b  ，其中向量a(2cosx,1)，b  (cosx, 3sin2x)，xR．  第11页 | 共18页  （1）若 f(x)1 3，且x[ ， ]，求x； 3 3  （2）若函数y2sin2x的图象按向量c(m,n)，(|m| )平移后得到函数y f(x)的图象，求实数m、n 2 的值．  【解答】解：（1）依题设 f(x)2cos2x 3sin2x12sin(2x )， 6  由12sin(2x )1 3， 6  3 得sin(2x ) ． 6 2    „ x„ ，  3 3   5  „ 2x „ ， 2 6 6    2x  ，即x ． 6 3 4 （2）函数y2sin2x的图象按向量c(m,n)平移后得到函数y2sin2(xm)n的图象， 即函数y f(x)的图象．  由（1）得 f(x)2sin(2x )1， 6  |m| ， 2  m ，n1． 12 18．（12分）甲、乙两人同时参加奥运志愿者选拔赛的考试，已知在备选的10道题中，甲能答对其中的6 道题，乙能答对其中的8道题．规定每次考试都从备选题中随机抽出3道题进行测试，至少答对2道题 才能入选． (I)求甲答对试题数的分布列及数学期望； (II)求甲、乙两人至少有一人入选的概率． 【解答】解：(I)依题意，甲答对试题数的可能取值为0，1，2，3， C3 1 则P(0) 4  ， C3 30 10 第12页 | 共18页C1 C2 3 P(1) 6 4  ， C3 10 10 C2 C1 1 P(2) 6 4  ， C3 2 10 C3 1 P(3) 6  ．． C3 6 10 的分布列为  0 1 2 3 1 3 1 1 P 30 10 2 6 1 3 1 1 9 甲答对试题数的数学期望为E0 1 2 3  ． 30 10 2 6 5 2 (II)设 甲 、 乙 两 人 考 试 合 格 的 事 件 分 别 为 A、 B， 则 P(A)P(2)P(3) ， 3 C2C1 C3 5656 14 P(B) 8 2 8   ． C3 120 15 10 因为事件A、B相互独立， 2 14 1 甲、乙两人考试均不合格的概率为P(A B)P(A) P(B)[1 ][1 ] ．   3 15 45 1 44 甲、乙两人至少有一人考试合格的概率为P1P(A B)1  ．  45 45 44 故甲、乙两人于少有一人考试合格的概率为 ．． 45 19．（12 分）在三棱锥 SABC中， ABC 是边长为 4 的正三角形，平面 SAC 平面 ABC， SASC 2 2，M 为AB的中点． （Ⅰ）证明：AC SB； （Ⅱ）求二面角SCM B的大小； （Ⅲ）求点B到平面SCM 的距离． 第13页 | 共18页【解答】证明：（Ⅰ）取AC中点D，连接DS 、DB． SASC ，BABC，  AC SD且AC DB， AC 平面SDB，又SB平面SDB， AC SB． （Ⅱ）解： SD AC，平面SAC 平面ABC，  SD平面ABC． 过D作DECM 于E，连接SE，则SECM ， SED为二面角SCM A的平面角． //1 由已知有DE AM ，所以DE1，又SASC 2 2，AC 4，SD2． 2 SD 在RtSDE中，tanSED 2， DE 二面角SCM A的大小为arctan2， 二面角SCM B的大小为arctan2． （Ⅲ）解：在RtSDE中，SE SD2 DE2  5，CM 是边长为4正ABC 的中线，CM 2 3． 1 1 S  CM SE 2 3 5 15， SCM 2  2 设点B到平面SCM 的距离为h， 1 1 由V V ，SD平面ABC，得 S h S SD， BSCM SCMB 3 SCM 3 CMB S SD 4 5 4 5 h CMB  ．即点B到平面SCM 的距离为 ． S 5 5 SCM 20．（12分）某企业2003年的纯利润为500万元，因设备老化等原因，企业的生产能力将逐年下降．若不 能进行技术改造，预测从今年起每年比上一年纯利润减少20万元，今年初该企业一次性投入资金600万 1 元进行技术改造，预测在未扣除技术改造资金的情况下，第n年（今年为第一年）的利润为500(1 ) 2n 万元(n为正整数）． 第14页 | 共18页（Ⅰ）设从今年起的前n年，若该企业不进行技术改造的累计纯利润为A 万元，进行技术改造后的累计纯 n 利润为B 万元（须扣除技术改造资金），求A 、B 的表达式； n n n （Ⅱ）依上述预测，从今年起该企业至少经过多少年，进行技术改造后的累计纯利润超过不进行技术改造 的累计纯利润？ 【解答】解：（Ⅰ）依题设，A (50020)(50040)(50020n)490n10n2； n 1 1 1 500 B 500[(1 )(1 )(1 )]600500n 100． n 2 22 2n 2n 500 （Ⅱ）B A (500n 100)(490n10n2) n n 2n 500 50 10n2 10n 10010[n(n1) 10]． 2n 2n 50 1 因为函数yx(x1) 10在( ，)上为增函数， 2n 2 50 50 当1„ n„ 3时，n(n1) 10„12 100； 2n 8 50 50 当n…4时，n(n1) 10…20 100． 2n 16 仅当n…4时，B  A ． n n 答：至少经过4年，该企业进行技术改造后的累计纯利润超过不进行技术改造的累计纯利润． 1 21．（12分）如图，P是抛物线C:y x2上一点，直线l过点P并与抛物线C在点P的切线垂直，l与抛 2 物线C相交于另一点Q． （Ⅰ）当点P的横坐标为2时，求直线l的方程； （Ⅱ）当点P在抛物线C上移动时，求线段PQ中点M 的轨迹方程，并求点M 到x轴的最短距离． 1 【解答】解：（Ⅰ）把x2代入y x2，得y2， 2 点P坐标为(2,2)． 1 由y x2，① 2 第15页 | 共18页得yx， 过点P的切线的斜率k 2， 切 1 1 直线l的斜率k   ， l k 2 切 1 直线l的方程为y2 (x2)， 2 即x2y60． 1 （Ⅱ）设Px ,y ,则y  x2． 0 0 0 2 0 过点P的切线斜率k x ，  切 0 当x 0时不合题意，x 0． 0 0 1 1 直线l的斜率k   ， l k x 切 0 1 1 直线l的方程为y x2  (xx )．② 2 0 x 0 0 2 方法一：联立①②消去y，得x2  xx2 20．设Q(x ，y )，M(x,y)． x 0 1 1 0 M 是PQ的中点，   x x 1 x 0 1    2 x  0  y 1 ( 1 x ) 1 x2  1  x 0 2 1.   x x 0 2 0 x2 2 0 0 0 1 消去x ，得yx2  1(x0)就是所求的轨迹方程． 0 2x2 1 1 由x0知x2 0， yx2  1…2 x2 1 21．  2x2 2x2 1 1 上式等号仅当x2  ,即x4 时成立，所以点M 到x轴的最短距离是 21． 2x2 2 方法二： 设Q(x ，y )，M(x,y)．则 1 1 1 1 x x 由y  x2，y  x2，x 0 1 ， 0 2 0 1 2 1 2 1 1 1 y  y  x2  x2  (x x )(x x )x(x x )， 0 1 2 0 2 1 2 0 1 0 1 0 1 第16页 | 共18页y  y 1 1  x 0 1 k  ， x  ， x x l x 0 x 0 1 0 1 将上式代入②并整理，得yx2  1(x0)就是所求的轨迹方程． 2x2 1 1 由x0知x2 0， yx2  1…2 x2 1 21．  2x2 2x2 1 1 上式等号仅当x2  ,即x4 时成立，所以点M 到x轴的最短距离是 21． 2x2 2 2 22．（14分）已知 f(x)4xax2  x3(xR)在区间[1，1]上是增函数． 3 （Ⅰ）求实数a的值组成的集合A； 1 （Ⅱ）设关于x的方程 f(x)2x x3的两个非零实根为x 、x ．试问：是否存在实数m，使得不等式 3 1 2 m2 tm1… |x x |对任意aA及t[1，1]恒成立？若存在，求m的取值范围；若不存在，请说明理 1 2 由． 【解答】解：（Ⅰ） f(x)42ax2x2， f(x)在[1，1]上是增函数，  f(x)…0对x[1，1]恒成立， 即x2 ax2„ 0对x[1，1]恒成立．① 设(x)x2 ax2， (1)1a2„ 0 ①  1„ a„1， (1)1a2„ 0 对x[1，1]，只有当a1时， f(1)0以及当a1时， f（1）0  A{a|1„ a„1}． 2 1 （Ⅱ）由4xax2  x3 2x x3，得x0，或x2 ax20， 3 3 △a2 80  x ，x 是方程x2 ax20的两非零实根，x x a，xx 2， 1 2 1 2 1 2 从而|x x | (x x )2 4xx  a2 8． 1 2 1 2 1 2 1„ a„1，|x x | a2 8„ 3．  1 2 要使不等式m2 tm1… |x x |对任意aA及t[1，1]恒成立， 1 2 第17页 | 共18页当且仅当m2 tm1…3对任意t[1，1]恒成立， 即m2 tm2…0对任意t[1，1]恒成立．② 设g(t)m2 tm2mt(m2 2)， ② g(1)m2 m2…0且g（1）m2 m2…0， m…2或m„ 2． 所以，存在实数m，使不等式m2 tm1… |x x |对任意aA及t[1，1]恒成立， 1 2 其取值范围是{m|m…2，或m„ 2}． 声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布 日期：2019/5/23 23:13:06；用户：15217760367；邮箱：15217760367；学号：10888156 第18页 | 共18页