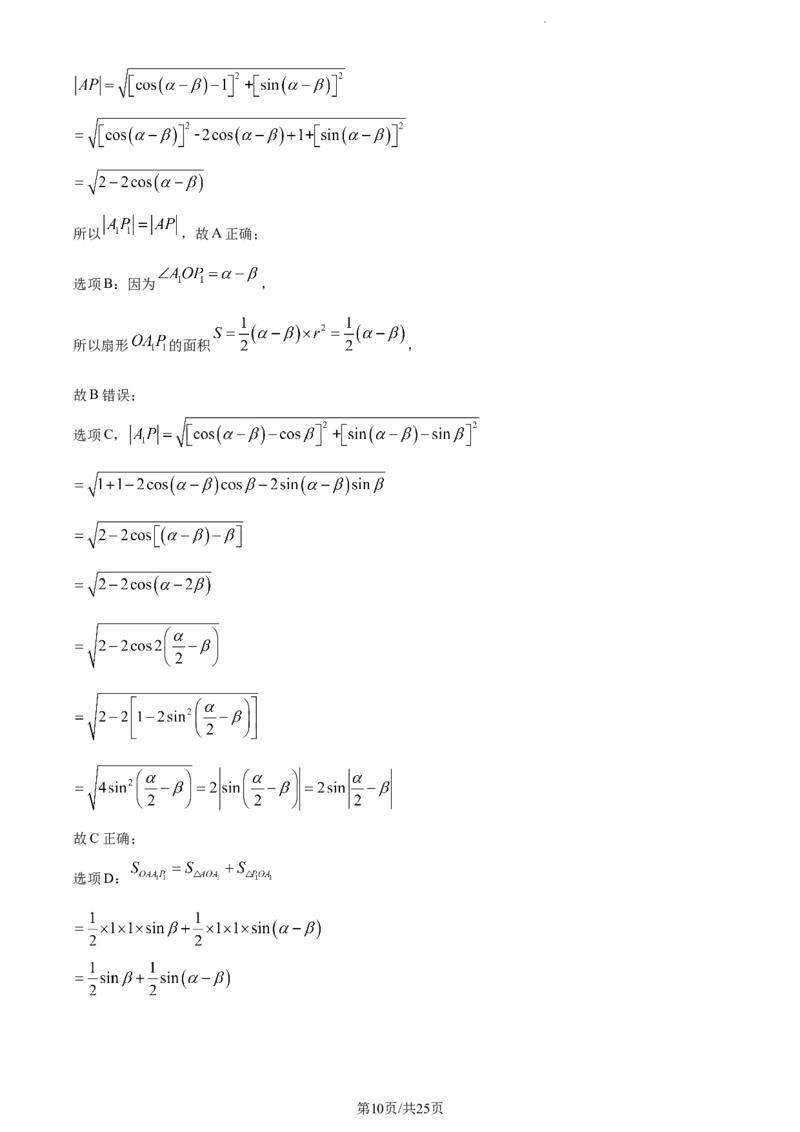文档内容
2023 年秋季德化一中第一次月考高三数学试卷
考试时间:120分钟;
第I卷(选择题)
一、单项选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一
项是符合题目要求的.)
1. 已知集合 , ,则 =( )
A. B. C. D.
【答案】B
【解析】
【分析】根据解一元二次不等式的方法,结合对数型函数的定义域、集合交集的定义进行求解即可.
【详解】 , ,
所以 , ,
则 ,
故选:B
2. “ ”是“ ”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
【答案】A
【解析】
【分析】根据充分必要条件的定义,结合指数函数性质,不等式的性质,即可判断.
【详解】不等式 等价于 ,
由 可推出 ,
由 不一定能推出 ,例如 时, ,但 ,
第1页/共25页
学科网(北京)股份有限公司所以“ ”是“ ”的充分不必要条件.
故选:A.
3. 已知 , ,则 ( )
A. B. C. D.
【答案】B
【解析】
【分析】利用两角差的正弦公式展开求出 ,然后利用两角和的正弦公式计算即可.
【详解】因为 ,
所以 ,
所以 .
故选:B
4. 已知函数 的最小正周期为 ,把函数 的图象向右平移 个单位长
度,所得图象对应函数解析式为( )
A. B.
C. D.
【答案】A
【解析】
【分析】先根据正弦函数最小正周期公式求出 ,在根据左加右减求出平移后的解析式.
第2页/共25页
学科网(北京)股份有限公司【详解】因为 ,所以 ,故 ,
则 ,
则向右平移 个单位长度后得到 .
故选:A
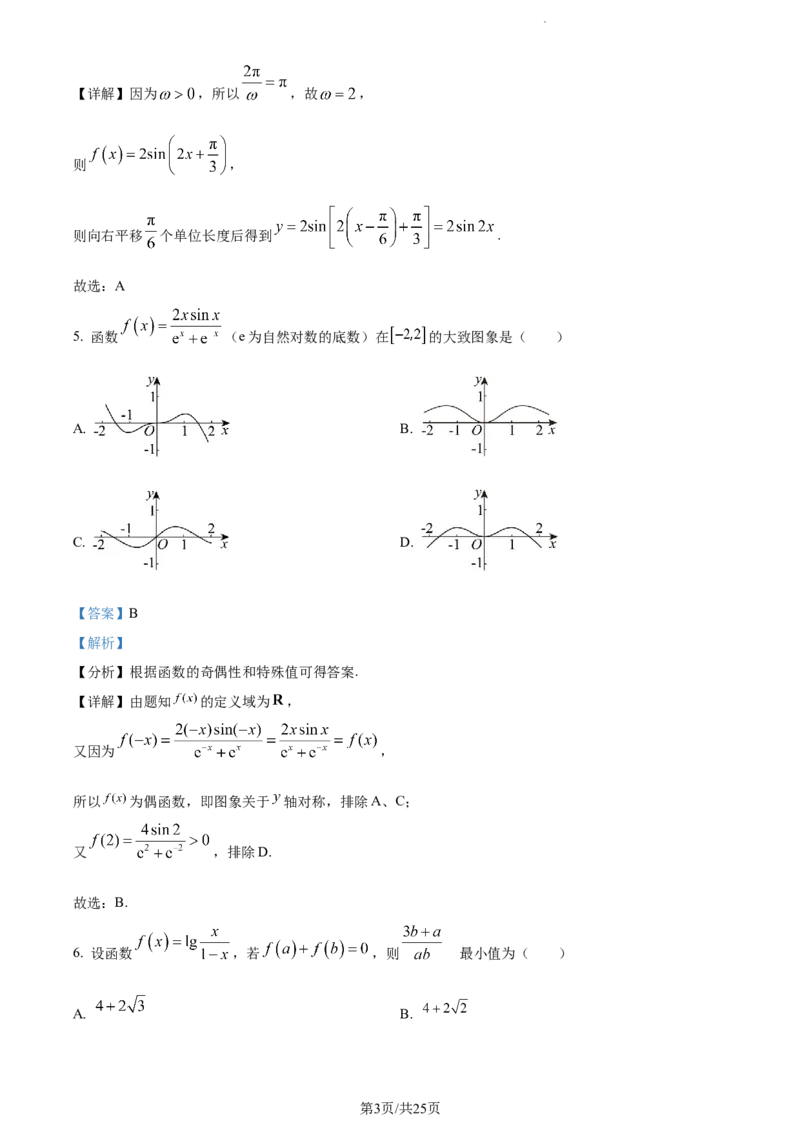
5. 函数 (e为自然对数的底数)在 的大致图象是( )
A. B.
C. D.
【答案】B
【解析】
【分析】根据函数的奇偶性和特殊值可得答案.
【详解】由题知 的定义域为 ,
又因为 ,
所以 为偶函数,即图象关于 轴对称,排除A、C;
又 ,排除D.
故选:B.
6. 设函数 ,若 ,则 最的小值为( )
A. B.
第3页/共25页
学科网(北京)股份有限公司C. D.
【答案】A
【解析】
【分析】求出函数 的定义域,根据给定等式求出 的关系,再利用“1”的妙用求解作答.
【详解】函数 中, ,解得 ,由 ,得 ,
且 ,则 ,整理得 ,
因此 ,当且仅当 ,即 取等
号,
由 且 ,得 ,
所以当 时, 取得最小值 .
故选:A
7. 用数学的眼光观察世界,神奇的彩虹角约为 .如图,眼睛与彩虹之间可以抽象为一个圆锥,设AO
是眼睛与彩虹中心的连线,AP是眼睛与彩虹最高点的连线,则称 为彩虹角.若平面ABC为水平面,
BC为彩虹面与水平面的交线, 为BC的中点, 米, 米,则彩虹( )的长度
约为( )(参考数据: , )
第4页/共25页
学科网(北京)股份有限公司A. 米 B. 米 C. 米 D. 米
【答案】A
【解析】
【分析】先求出圆锥的母线长,再求出圆锥的底面半径,连接 , , ,进而在 中求
,最后利用弧长公式求得彩虹长度.
【详解】
在 中,由勾股定理,
可得: ,
连接PO,则在 中, ,
连接OB,OC,OM,则在 中,
,
故 , ,
则彩虹( )的长度约为 .
故选:A
8. 设 , , ,则( )
A. B. C. D.
【答案】A
【解析】
【分析】构造函数 ,利用导数求出函数的单调区间,即可比较 ,构造函数
第5页/共25页
学科网(北京)股份有限公司,利用导数判断函数的单调性,即可比较 ,进而可得出答案.
【详解】令 ,则 ,
当 时, ,所以 在 上单调递减,
所以 ,即 ,
所以 ,即 ,
令 ,则 ,
令 ,
因为函数 在 上都是减函数,
所以 在 上是减函数,
所以 ,
即 ,
所以函数 在 上是减函数,
所以 ,
即 ,所以 ,所以 ,
综上所述, .
故选:A.
【点睛】关键点点睛:构造函数 和 是解决本题 关的键.
二、多项选择题(本大题共4小题,每小题5分,共20分,在每小题给出的四个选项中,有
第6页/共25页
学科网(北京)股份有限公司多个选项符合题目要求,全部选对的得5分,选对但不全的得2分,有选错的得0分.)
9. 设 ,则下列不等式中恒成立的是( )
A. B. C. D.
【答案】AB
【解析】
【分析】利用作差比较逐一判断即可.
【详解】A:因为 ,所以 ,因此本选项正确;
B:因为 ,所以 ,因此本选项正确;
C:因 为,所以 ,因此本选项不正确;
D:因为 ,所以 ,因此本选项不正确,
故选:AB
10. 在 中,若 ,则( )
A. B.
C. D.
【答案】ABD
【解析】
【分析】对于选项A,由三角形大边对大角和正弦定理可判断;
对于选项B,由余弦函数单调性可判断;
对于选项C,由正弦的二倍角公式可判断;
对于选项D,由余弦的二倍角公式可判断
【详解】在 中,若 ,由三角形中大边对大角,可得 ,又由正弦定理,可知
,故A选项正确;
第7页/共25页
学科网(北京)股份有限公司又由余弦函数在 上单调递减,可知 ,故B选项正确;
由 和 ,当 时, ,所以 ,故
C选项错误;
由 , ,由A选项可知正确,故D选项正确.
故选:ABD
11. 已知定义在 上的函数 满足 ,在下列不等关系中,一定成立的是( )
A. B.
C. D.
【答案】AD
【解析】
【分析】构造函数 ,求导得到 在R上单调递减,然后根据单调性比较大小即可.
【详解】因为 ,所以
令 ,则 ,
因为 , ,所以 ,所以 在R上单调递减,
,即 ,即 ,故A正确,B错;
,即 ,即 ,故C错,D正确.
故选:AD.
12. 如图所示,设单位圆与x轴的正半轴相交于点 ,以x轴非负半轴为始边作锐角 , , ,
它们的终边分别与单位圆相交于点 , ,P,则下列说法正确的是( )
第8页/共25页
学科网(北京)股份有限公司A.
B. 扇形 的面积为
C.
D. 当 时,四边形 的面积为
【答案】ACD
【解析】
【分析】由题意圆的半径 在平面直角坐标系中写出 的坐标用两点间的距离公式计算
即可得A选项;选项B,利用扇形的面积公式计算即可;选项C,利用两点间的距离公式写出 化简即
可;选项D, 分别表示出来化简即可
【详解】由题意圆的半径
选项A:由题意得
所以
第9页/共25页
学科网(北京)股份有限公司所以 ,故A正确;
选项B:因为 ,
所以扇形 的面积 ,
故B错误;
选项C,
故C正确;
选项D:
第10页/共25页
学科网(北京)股份有限公司因为 ,
所以
故D正确
故选:ACD.
第II卷(非选择题)
三、填空题(本大题共4小题,每小题5分,共20分.)
13. 已知锐角 满足 ,则 _______________.
【答案】
【解析】
【分析】利用同角三角函数基本关系及倍角公式变形计算即可.
【详解】因为 ,所以 ,又 为锐角,
所以 ,即 ,
所以 .
第11页/共25页
学科网(北京)股份有限公司故答案为:
14. 中华人民共和国国歌有84个字,37小节,奏唱需要45秒,某校周一举行升旗仪式,旗杆正好处在坡
度 的看台的某一列的正前方,从这一列的第一排和最后一排测得旗杆顶部的仰角分别为 和 ,第
一排和最后一排的距离为 米如图所示,旗杆底部与第一排在同一个水平面上,则旗杆 的高度为
______米.
【答案】
【解析】
【分析】根据题意求得角,利用正弦定理求得边长,再根据直角三角形边角关系求出旗杆的高度即可.
【详解】由题意可知 , ,
所以 ,
由正弦定理可知在 中 ,
所以 ,
所以在 中 ,
故答案为:
15. 已知 ,则 的最小值为______.
第12页/共25页
学科网(北京)股份有限公司【答案】
【解析】
【分析】将代数式 与 相乘,展开后利用基本不等式可求得 的最小值.
【详解】
,
当且仅当 ,解得 , ,
又因为 ,所以 时等号成立.
因此, 的最小值为 .
故答案为: .
【点睛】本题考查基本不等式求代数式的最值,考查了“ ”的代换的应用,考查计算能力,属于基础题.
16. 已知函数 ,过点 有两条直线与曲线 相切,则实数 的取值范围是
________.
【答案】
【解析】
【分析】根据导数的几何意义及直线的点斜式方程,将所求问题转化为方程的根的问题,利用导数法求函
数的最值即可求解.
【详解】由 ,得 ,
第13页/共25页
学科网(北京)股份有限公司设切点为 ,则
切线方程为: .
因为过点 有两条直线与曲线 相切,
所以 有两根,即 有两根.
令 ,则 ,
令 即 解得 ;
令 即 解得 ;
在 递减,在 递增.
当 时, 取得极小值也为 的最小值,
所以 ,
故实数m的取值范围是 .
故答案为: .
四、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)
17. 已知 ,角 的顶点为坐标原点,始边与 轴的非负半轴重合,终边经过点
,且 .求
第14页/共25页
学科网(北京)股份有限公司(1) ;
(2) .
【答案】(1)
(2)
【解析】
【分析】(1)根据题意利用三角函数定义即可求得 ,再由诱导公式代入计算即
可得出结果;
(2)利用(1)中的三角函数值以及角的范围可求出 ,即可得 .
【小问1详解】
由 ,可得 ,
根据三角函数定义可知 ,
所以 ,
即 ;
【小问2详解】
由 且 可知 ,
又 ,可得 ;
第15页/共25页
学科网(北京)股份有限公司所以 ,
可得 .
18. 已知 的内角 的对边分别为 , .
(1)求A;
(2)若 ,求 的面积的最大值.
【答案】(1) ;
(2) .
【解析】
【分析】(1)利用正弦定理边化角,再利用和角的正弦化简求解作答;
的
(2)利用余弦定理结合均值不等式求出 最大值,再由面积公式求解即得;或利用正弦定理及三角形
面积公式结合三角形的性质即得.
【小问1详解】
由正弦定理及 ,得 ,
,
,即 ,
,又 ,
,又 ,
;
【小问2详解】
法一:在 中,由余弦定理得 ,
第16页/共25页
学科网(北京)股份有限公司,即 ,当且仅当 时等号成立,
,即 的面积的最大值为 ;
法二:在 中,由正弦定理得 ,
,
,
又 ,
所以当 ,即 时, 的面积的取得最大值 .
19. 已知函数 ,当 时,函数 取得极值.
(1)若 在 上为增函数,求实数m的取值范围;
(2)若 时,方程 有两个根,求实数m的取值范围.
【答案】(1)
(2)
【解析】
【分析】(1)根据函数极值的定义,结合导数的性质进行求解即可;
(2)构造新函数,利用导数的性质,结合函数零点的性质进行求解即可.
【小问1详解】
第17页/共25页
学科网(北京)股份有限公司由 ,则 ,
因为 时, 取到极值,所以 ,解得 .
又当 时, ,
当 时, ,函数单调递增,当 时, ,函数单调递减,当 时,
,函数单调递增,
故当 时,函数 取得极值,符合题意.
要使 在 上为增函数,则 或 ,所以 或 .
即实数 的取值范围为 .
【
小问2详解】
令 ,由(1)得 ,且 ,
故 , ,则 ,
当 时,令 ,解得 ,令 ,解得 ,
所以 的递增区间为 ,递减区间为 ,
故 ,而 , ,故 .
要使 有两个根,则 .
第18页/共25页
学科网(北京)股份有限公司即实数 的取值范围为 .
20. 设 是函数 的两个零点,且 的最小值是 .
(1)求函数 的解析式;
(2)已知实数 满足 ,且对 恒有 ,求 的最小值.
【答案】(1)
(2)
【解析】
【分析】(1)根据三角函数图象性质可知周期 ,可计算得 ,即可求出 ;
(2)易知对 可得 ,即只需 ,可求得 ,再由基本不
等式即可求得 的最小值为 .
【小问1详解】
因为函数 的两个零点之间的距离最小值为 ,
所以周期 ,
可得 ,解得 ;
即函数 ;
第19页/共25页
学科网(北京)股份有限公司所以函数 的解析式为 ;
【小问2详解】
由 可得 ,所以
又 恒有 ,
只需 ,所以 ,解得 ,
即 ;
易知 ,
当且仅当 时,等号成立;
即可得 的最小值为 .
21. 如图,有一景区的平面图是一半圆形,其中直径 长为 和 两点在半圆弧上,满足
.设 .
(1)现要在景区内铺设一条观光道路,由线段 和 组成,则当 为何值时,观光道路的总
长 最长,并求 的最大值;
(2)若要在景区内种植鲜花,其中在 和 内种满鲜花,在扇形 内种一半面积的鲜花,
则当 为何值时,鲜花种植面积 最大?
第20页/共25页
学科网(北京)股份有限公司【答案】(1) 时,观光道路的总长 最长, 的最大值为5
(2)当 时,鲜花种植面积 最大
【解析】
【 分 析 】 ( 1 ) 作 出 辅 助 线 , 表 达 出 , , 从 而 求 出
,配方后得到当 ,即 时, 取得最大值,
最大值为5;
(2)表达出 , ,扇形COD的面积 ,从而求出故
,求导得到其单调性,在当 时, 取得极大值,也是最大值,得到答
案.
【小问1详解】
取BC的中点M,AD的中点N,连接OM,ON,由垂径定理可得:OM⊥BC,ON⊥AD,
由题意得: ,
,故 ,
则 ,
因为 ,所以 , ,
故当 ,即 时, 取得最大值,最大值为5;
第21页/共25页
学科网(北京)股份有限公司【小问2详解】
,
,
扇形COD的面积 ,
故 ,
则 ,
因为 ,所以 ,
故当 时, 时, ,当 时, ,
故 时, 单调递增,当 时, 单调递减,
当 时, 取得极大值,也是最大值,
故当 时,鲜花种植面积 最大.
22. 已知函数 , 为其导函数.
(1)若 ,求 的单调区间;
第22页/共25页
学科网(北京)股份有限公司(2)若关于 的方程 有两个不相等的实根,求实数 的取值范围.
【答案】(1) 的单调减区间为 ,增区间为
(2)
【解析】
【分析】(1)根据函数 单调性与导数的关系确定函数的单调区间即可;
(2)将方程 有两个不相等的实根,转化为函数 ,在 上有两个零
点问题,求导数 从而讨论函数单调性,结合零点存在定理判断是否符合题意,从而可得实数 的取
值范围.
【小问1详解】
解:函数 , ,则 ,
令 ,则 ,设 ,则
,得 ,
故 时, ,函数 即 单调递减, 时, ,函数 即
单调递增,
所以 ,又 时, ,又 ,
所以 时, ,函数 单调递减, 时, ,函数 单调递增,
故 的单调减区间为 ,增区间为 ;
【小问2详解】
解:关于 的方程 有两个不相等的实根,即函数 ,在 上有
第23页/共25页
学科网(北京)股份有限公司两个零点,
又 ,
①当 时, ,得 ,所以当 时, ,函数 单调递减,当
时, ,函数 单调递增,
所以 ,又 时, , ,则函数 在 上有
两个零点;
②当 时, ,得 , ,
(i)当 时, ,此时 恒成立,函数 单调递增,在 上不可能有两个
零点,不符合题意;
(ii)当 时, ,则当 时, ,函数 单调递增,
时, ,函数 单调递减,当 时, ,函数 单调递
增,
所以 , ,故函数
在区间 无零点,在 不可能存在两个零点,故不符合题意;
(iii)当 时, ,则当 时, ,函数 单调递增,
时, ,函数 单调递减,当 时, ,函数
单调递增,
又 ,故函数 在区间 无零点,在 不可能存在两个零点,
故不符合题意;
③当 时,方程只有一个实根1,不合题意;
第24页/共25页
学科网(北京)股份有限公司综上,实数 的取值范围 .
【点睛】本题考查的是函数单调性、函数零点问题与导数的综合,难度较大.解决含参方程问题得关键是
将含参方程转化为函数零点问题,从而利用函数单调性与导数的关系,对参数进行讨论先确定单调性,再
结合零点存在定理及函数的极值判断各单调区间零点个数,从而求得参数范围,需要注意的是取值判断函
数值符号的过程可结合函数的极限思想看开区间端点处的函数值趋势得正负.
第25页/共25页
学科网(北京)股份有限公司