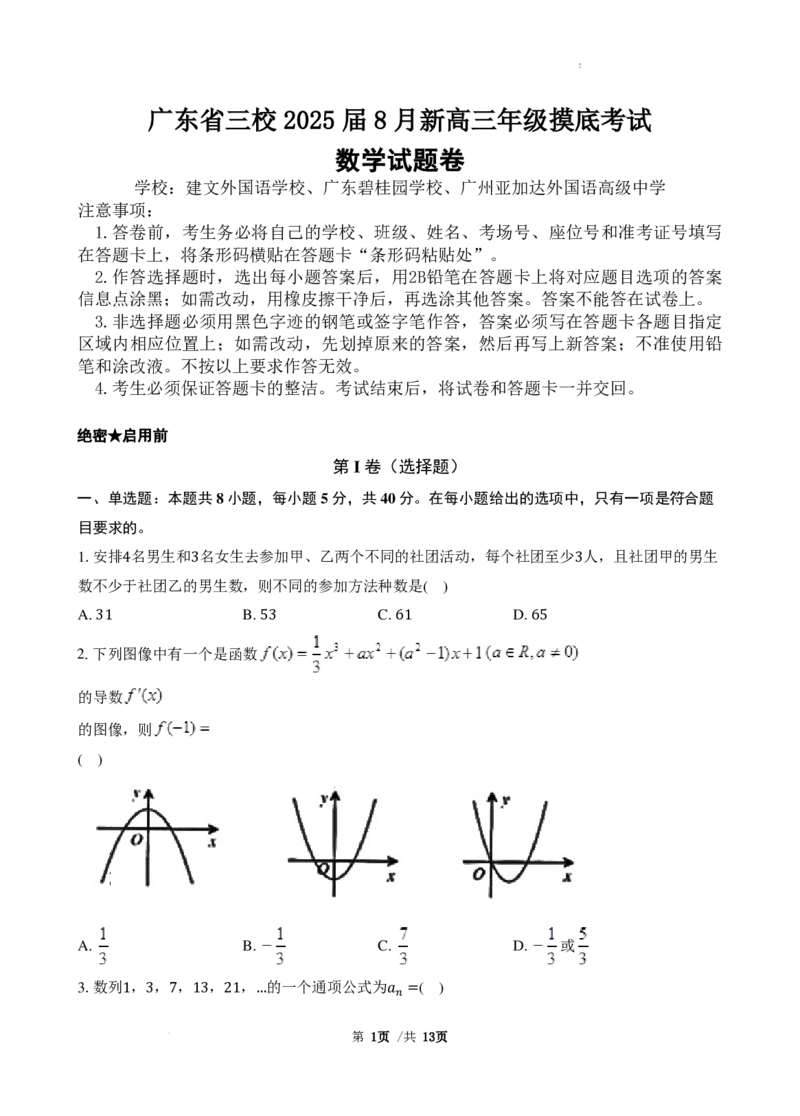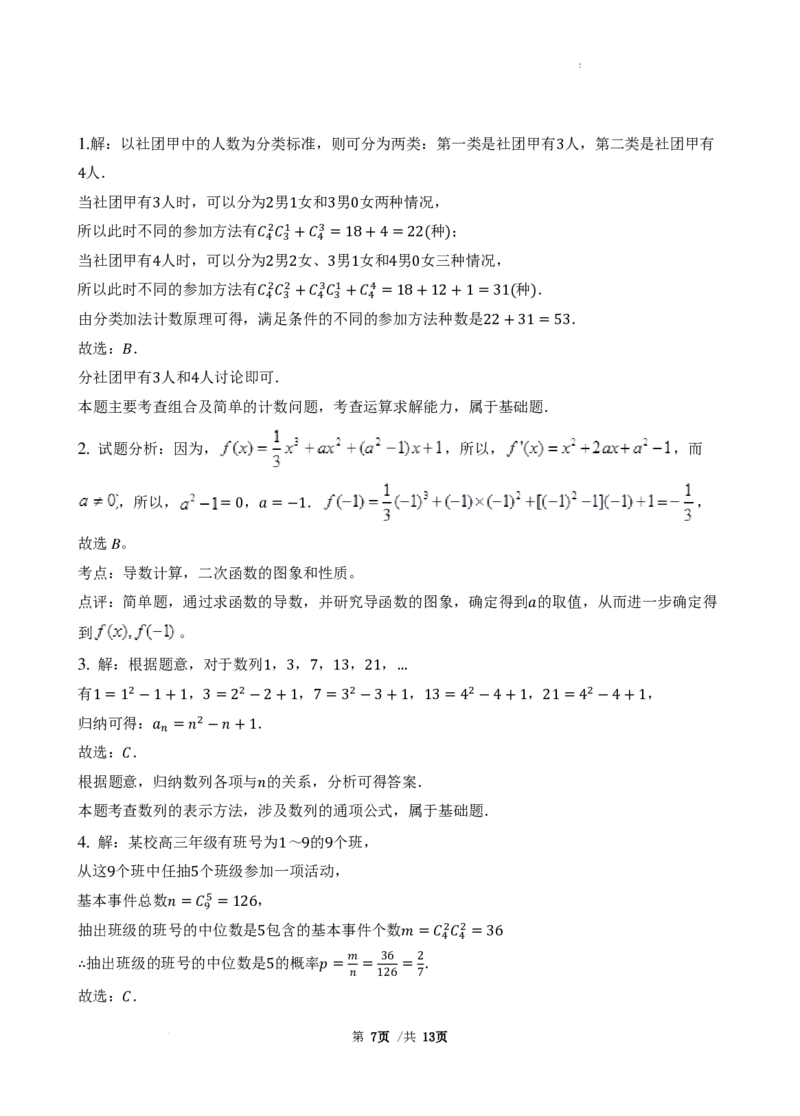文档内容
广东省三校 2025 届 8 月新高三年级摸底考试
数学试题卷
学校:建文外国语学校、广东碧桂园学校、广州亚加达外国语高级中学
注意事项:
1.答卷前,考生务必将自己的学校、班级、姓名、考场号、座位号和准考证号填写
在答题卡上,将条形码横贴在答题卡“条形码粘贴处”。
2.作答选择题时,选出每小题答案后,用2B铅笔在答题卡上将对应题目选项的答案
信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案。答案不能答在试卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定
区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅
笔和涂改液。不按以上要求作答无效。
4.考生必须保证答题卡的整洁。考试结束后,将试卷和答题卡一并交回。
绝密★启用前
第I卷(选择题)
一、单选题:本题共8小题,每小题5分,共40分。在每小 题给出的选项中,只有一项是符合题
目要求的。
1.安排 名男 生和 名女生去参加甲、乙两个不同的社团活动,每个社团至少 人,且社团甲的男生
数不少于 4 社团乙的 3 男生数,则不同的参加方法种数是( ) 3
A. B. C. D.
31 53 61 65
2.下列图像中有一个是函数
的导数
的图像,则
( )
A. B. C. D. 或
3.数列 , , , , , 的一个通项公式为 ( )
1 3 7 13 21 … 𝑎𝑎𝑛𝑛 =
第 1页 /共 13页
学科网(北京)股份有限公司A. B. C. D.
2 2 2 2
4.某
𝑛𝑛
校
−
高
𝑛𝑛
三 年级有班号为 ~
𝑛𝑛
的
−𝑛𝑛
个
−
班
1
, 从这 个
𝑛𝑛
班中
−
任
𝑛𝑛
抽
+1
个班级参加
𝑛𝑛
一
−
项
2
活
𝑛𝑛
动,则抽出班级的班
号的中位数是 的概率等于 1( 9 ) 9 9 5
A. 5 B. C. D.
5 5 2 4
5.在
7
等差数列
9 7 9
中, , , ( )
A. =3 =10 =B. C. D.
6.在一次联考后,某校对甲、乙两个文科班的数学考试成绩进行分析,规定:大于或等于 分为
13 17 21 23
优秀, 分以下为非优秀,统计成绩后,得到如下 列联表:
120
120 2×2
𝛼𝛼 0.05 0.01 0.005 0.001
优秀 非优秀 合计 𝑥𝑥𝛼𝛼 3.841 6.635 7.879 10.828
甲班人数
乙班人数 10 50 60
合计 20 30 50
附: 30 80 110 ,其中 .
2
2 𝑛𝑛(𝑎𝑎𝑎𝑎−𝑏𝑏𝑏𝑏)
𝜒𝜒 =(𝑎𝑎+𝑏𝑏)(𝑏𝑏+𝑎𝑎)(𝑎𝑎+𝑏𝑏)(𝑏𝑏+𝑎𝑎) 𝑛𝑛 =𝑎𝑎+𝑏𝑏+𝑏𝑏+𝑎𝑎
根据独立性检验,可以认为数学考试成绩与班级有关系的把握为( )
A. B. C. D.
7.某中学数学组来了 名即将毕业的大学生进行教学实习活动,现将他们分配到高一年级的 , ,
95% 99.5% 99.9% 99%
三个班实习,每班至 5 少一名,最多两名,则不同的分配方案有( ) 1 2
3A. 种 B. 种 C. 种 D. 种
8.若30关于 的不等式 90 恒1成50立,则实数 的最1大80值为( )
𝑥𝑥 1 2
A.
𝑥𝑥 𝑒𝑒 +𝑥𝑥
B
+
.
2 ln𝑥𝑥 ≥𝑚𝑚𝑥𝑥 +ln𝑚𝑚
C.
𝑚𝑚
D.
2
1 𝑒𝑒 2
二、
2
多选题:本题共3小题,
4
共18分。在每小题1给出的选项中,有多𝑒𝑒项符合题目要求。
9.给出下列命题,其中正确的是( )
A. 对于独立性检验 的值越大,说明两事件相关程度越大
2
B. 若随机变量 ~𝐾𝐾 , ,则
2
𝜉𝜉 𝑁𝑁(1,𝜎𝜎 ) 𝑃𝑃(𝜉𝜉 ≤4)=0.75 𝑃𝑃(𝜉𝜉 ≤−2)=0.25
第 2页 /共 13页
学科网(北京)股份有限公司C. 若 ~ ,则
1
D. 已𝑋𝑋知样𝐵𝐵本(9点,3) 𝐷𝐷(2𝑋𝑋+1)=8 组成一个样本,得到回归直线方程 ,且 ,
̂ −
剔除两个样本点 (𝑥𝑥𝑖𝑖,𝑦𝑦𝑖𝑖)(𝑖𝑖 和 =1,2,3,⋯ 得 ,1 到 0 新 ) 的回归直线的斜率为 ,则新的回 𝑦𝑦 归 = 方 2 程 𝑥𝑥 为 −0.4 𝑥𝑥 = 2
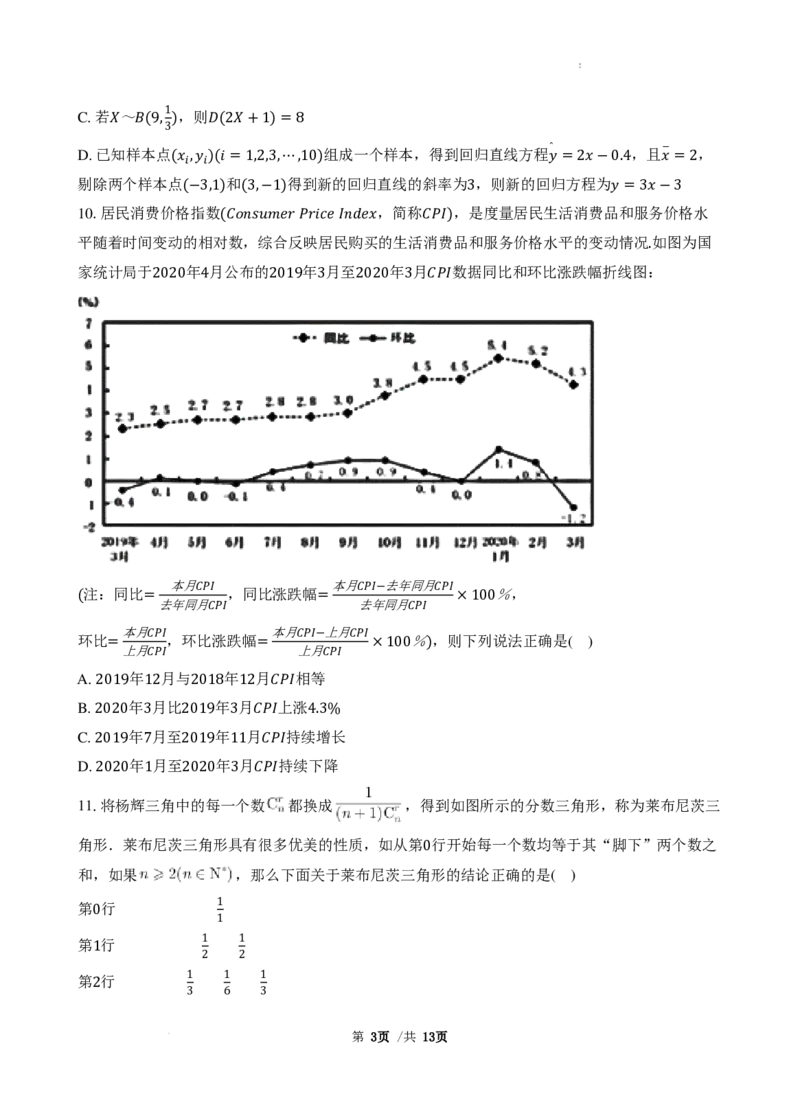
10.居民消费价格
(−
指
3
数
,1) (3,−1)
,简称 ,
3
是度量居民生活消费品
𝑦𝑦
和
=
服
3𝑥𝑥
务
−
价
3
格水
平随着时间变动的相对数,综合反映居民购买的生活消费品和服务价格水平的变动情况如图为国
(𝐶𝐶𝐶𝐶𝑛𝑛𝐶𝐶𝐶𝐶𝑚𝑚𝑒𝑒𝐶𝐶 𝑃𝑃𝐶𝐶𝑖𝑖𝑏𝑏𝑒𝑒 𝐼𝐼𝑛𝑛𝑎𝑎𝑒𝑒𝑥𝑥 𝐶𝐶𝑃𝑃𝐼𝐼)
家统计局于 年 月公布的 年 月至 年 月 数据同比和环比涨跌幅折线图:
.
2020 4 2019 3 2020 3 𝐶𝐶𝑃𝑃𝐼𝐼
本月 本月 去年同月
注:同比 ,同比涨跌幅 %,
去年同月 去年同月
𝐶𝐶𝑃𝑃𝐼𝐼 𝐶𝐶𝑃𝑃𝐼𝐼− 𝐶𝐶𝑃𝑃𝐼𝐼
( = = ×100
本月 𝐶𝐶𝑃𝑃𝐼𝐼 本月 上月 𝐶𝐶𝑃𝑃𝐼𝐼
环比 ,环比涨跌幅 %,则下列说法正确是( )
上月 上月
𝐶𝐶𝑃𝑃𝐼𝐼 𝐶𝐶𝑃𝑃𝐼𝐼− 𝐶𝐶𝑃𝑃𝐼𝐼
A. = 年𝐶𝐶𝑃𝑃月𝐼𝐼 与 年 月= 相等𝐶𝐶 𝑃𝑃𝐼𝐼 ×100 )
B. 2019 年 1 月 2 比 201 年 8 月 12 𝐶𝐶 上 𝑃𝑃𝐼𝐼 涨
C. 2020 年 3 月至 2019 年 3 月 𝐶𝐶𝑃𝑃𝐼𝐼 持续 4. 增 3% 长
D. 2019 年 7 月至 2019 年 11 月 𝐶𝐶𝑃𝑃 持 𝐼𝐼 续下降
2020 1 2020 3 𝐶𝐶𝑃𝑃𝐼𝐼
11.将杨辉三角中的每一个数 都换成 ,得到如图所示的分数三角形,称为莱布尼茨三
角形.莱布尼茨三角形具有很多优美的性质,如从第 行开始每一个数均等于其“脚下”两个数之
和,如果 ,那么下面关于莱布尼茨三角 0 形的结论正确的是( )
第 行
1
第0行 1
1 1
第1行 2 2
1 1 1
2 3 6 3
第 3页 /共 13页
学科网(北京)股份有限公司第 行
1 1 1 1
3 4 1 2 12 4
…第…行 … …
𝑛𝑛 ……
A. 当 是偶数时,中间的一项取得最大值;当 是奇数时,中间的两项相等,且同时取得最大值
B. 第𝑛𝑛行第 个数是 𝑛𝑛
1
8 2 72
C.
D.
第II卷(非选择题)
三、填空题:本题共3小题,每小题5分,共15分。
12.已知 ,若 ,则 ______.
6 7
13.已知(1~+𝑥𝑥)(𝑎𝑎−𝑥𝑥) =,𝑎𝑎则0+落𝑎𝑎1在𝑥𝑥区+间⋯+𝑎𝑎7𝑥𝑥 中𝑎𝑎0的+概𝑎𝑎率1+为⋯ + 𝑎𝑎 7参=考0数据𝑎𝑎:3 =
2
, ,
𝑋𝑋 𝑁𝑁(1.4,0.05 ) 𝑋𝑋 (1.35,1.45) .( 𝑃𝑃(𝜇𝜇−𝜎𝜎 <𝑋𝑋 <
𝜇𝜇14+.若𝜎𝜎)曲=线0.683 𝑃𝑃(𝜇𝜇−2𝜎𝜎不<存𝑋𝑋在<垂𝜇𝜇+直2于𝜎𝜎)轴=的0.9切5线4 ,𝑃𝑃则(𝜇𝜇实−数3𝜎𝜎的<取𝑋𝑋值<范𝜇𝜇围+是3𝜎𝜎_)_=__0_._9.97 )
𝑎𝑎 2 𝑥𝑥
𝑓𝑓(𝑥𝑥)=2𝑥𝑥 −𝑒𝑒 𝑦𝑦 𝑎𝑎
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15. 本小题 分
若函数 , 的图象与直线 , , 所围成的封闭
( 13 )
图形的𝑓𝑓面(𝑥𝑥积)为=𝐶𝐶𝑖𝑖𝑛𝑛𝑥𝑥−𝑏𝑏𝐶𝐶𝐶𝐶𝑥𝑥.+ 𝑎𝑎𝑥𝑥+1 𝑥𝑥 ∈[0,2𝜋𝜋] 𝑥𝑥 =0 𝑥𝑥 =𝜋𝜋 𝑦𝑦=0
1 2
求 的值; 2𝜋𝜋 +𝜋𝜋+2
求函数 单调区间及最值;
(1) 𝑎𝑎
求函数 在区间 上的零点个数.
(2) 𝑓𝑓(𝑥𝑥)
(3) 𝑔𝑔(𝑥𝑥)=𝑓𝑓(𝑥𝑥)−𝑚𝑚 𝑥𝑥 ∈[0,2𝜋𝜋]
16. 本小题 分
设函(数 15 ) 且 , 为 的导函数.
1 𝑥𝑥
当 𝑓𝑓(𝑥𝑥)时=,(1求+𝑛𝑛) (𝑛𝑛∈展𝑁𝑁开, 式𝑛𝑛二>项1式) 系𝑓𝑓数′(𝑥𝑥最)大𝑓𝑓的(𝑥𝑥项);
1 𝑥𝑥
(1)对𝑥𝑥任=意5的实数 (,1证+明𝑛𝑛): ;
𝑓𝑓(2𝑥𝑥)+𝑓𝑓(2) ′
(2) 𝑥𝑥 2 >𝑓𝑓 (𝑥𝑥)
第 4页 /共 13页
学科网(北京)股份有限公司是否存在 ,使得 对 ,且 恒成立?若存在,求出
𝑛𝑛 1 𝑘𝑘
(3的)值并证明𝑎𝑎你∈的𝑁𝑁结论;若𝑎𝑎𝑛𝑛不<存∑在𝑘𝑘=,1(请1说+明 𝑘𝑘)理<由(.𝑎𝑎+ 1)𝑛𝑛 ∀𝑛𝑛 ∈𝑁𝑁 𝑛𝑛 >1
𝑎𝑎
17. 本小题 分
十七世纪至十八世纪的德国数学家莱布尼兹是世界上第一个提出二进制记数法的人,用二进制记
( 15 )
数只需数字 和 ,对于整数可理解为逢二进一,例如:自然数 在二进制中就表示为 , 表示
为 , 表 0 示 1 为 , 表示为 ,发现若 ,可表 1 示为二进制表达式 (1)2 2
(10)2 3 (1 , 1 则 )2 5 (101)2 𝑛𝑛 ∈𝑁𝑁 ,其中 , 或
𝑘𝑘 𝑘𝑘−1 1
(𝑎𝑎0𝑎𝑎1𝑎𝑎2… . 𝑎𝑎 𝑘𝑘−1𝑎𝑎𝑘𝑘)2 𝑛𝑛 =𝑎𝑎𝑛𝑛⋅2 +𝑎𝑎1⋅2 +⋯+𝑎𝑎𝑘𝑘−1⋅2 +𝑎𝑎𝑛𝑛 𝑎𝑎0 =1 𝑎𝑎𝑖𝑖 =0 1(𝑖𝑖 =
记 ,求证: ;
1,2,…,𝑘𝑘)
(1)
记
𝑆𝑆(𝑛𝑛)
为
=
整
𝑎𝑎
数0+ 的 𝑎𝑎1二
+
进
⋯
制
+
表 𝑎𝑎𝑘𝑘达−1式
+
中 𝑎𝑎𝑘𝑘的 的个数
𝑆𝑆
,
(1
如
6𝑛𝑛+3)=
,
𝑆𝑆(4𝑛𝑛+3)
.
(Ⅰ2) 求 𝐼𝐼(𝑛𝑛) ; 𝑛𝑛 0 𝐼𝐼(2)=1 𝐼𝐼(3)=0
(Ⅱ) 求 𝐼𝐼(80) 用数字作答 .
255 𝐼𝐼(𝑛𝑛)
( ) ∑𝑛𝑛=12 ( )
18. 本小题 分
年 月 日,中国科学技术大学潘建伟团队成功构建 个光子的量子计算机原型机“九章
( 17 )
三号”,求解高斯玻色取样数学问题比目前全球最快的超级计算机快一亿亿倍相较传统计算机的
2023 10 11 255
经典比特只能处于 态或 态,量子计算机的量子比特 可同时处于 与 的叠加态,故每个量
.
子比特处于 态或 态是基于概率进行计算的现假设某台量子计算机以每个粒子的自旋状态作为量
0 1 (𝑞𝑞𝐶𝐶𝑏𝑏𝑖𝑖𝑞𝑞) 0 1
子比特,且自旋状态只有上旋与下旋两种状态,其中下旋表示“ ”,上旋表示“ ”,粒子间的
0 1 .
自旋状态相互独立现将两个初始状态均为叠加态的粒子输入第一道逻辑门后,粒子自旋状态等可
0 1
能的变为上旋或下旋,再输入第二道逻辑门后,粒子的自旋状态有 的概率发生改变,记通过第二
.
道逻辑门后的两个粒子中上旋粒子的个数为 .
𝑝𝑝
若通过第二道逻辑门后的两个粒子中上旋𝑋𝑋粒子的个数为 ,且 ,求两个粒子通过第一道逻
1
(辑1)门后上旋粒子个数为 的概率; 2 𝑝𝑝=3
若一条信息有 种可能的情况且各种情况互斥,记这些情况发生的概率分别为
2
, , , ,则称 其中 为这条信息的信息熵
(2) 𝑛𝑛(𝑛𝑛>1,𝑛𝑛 ∈𝑁𝑁∗)
试 𝑝𝑝1求 𝑝𝑝 两2个 … 粒子 𝑝𝑝 通 𝑛𝑛 过第二 𝐻𝐻 道 = 逻 𝑓𝑓 辑 (𝑝𝑝 门1) 后 + 上 𝑓𝑓 旋 (𝑝𝑝2粒 ) 子 + 个 ⋯ 数 + 为 𝑓𝑓(𝑝𝑝𝑛𝑛的 )( 信息熵 𝑓𝑓(𝑥𝑥 ; )= −𝑥𝑥𝑥𝑥𝐶𝐶𝑔𝑔2𝑥𝑥) .
将一个下旋粒子输入第二道逻辑门,当粒子输出后变为上旋粒子时则停止输入,否则重复输入
𝑋𝑋 𝐻𝐻
(3)
第 5页 /共 13页
学科网(北京)股份有限公司第二道逻辑门直至其变为上旋粒子,设停止输入时该粒子通过第二道逻辑门的次数为
证明:当 无限增大时, 的数学期望趋近于一个常数.
𝑌𝑌(𝑌𝑌 =
1,2,3,…,𝑛𝑛,…). 𝑛𝑛 𝑌𝑌
19. 本小题 分
已知函数 ,
( 17 )
求曲线 在点 处的切线方程
𝑓𝑓(𝑥𝑥)=𝑥𝑥ln𝑥𝑥+1 𝑔𝑔(𝑥𝑥)=sin𝑥𝑥.
证明:函数 在区间 内有且只有一个极值点
(1) 𝑦𝑦=𝑓𝑓(𝑥𝑥) (1,1) ;
证明: .
(2) ℎ(𝑥𝑥)=𝑓𝑓(𝑥𝑥)−𝑔𝑔(𝑥𝑥) (0,1) ;
(3) 𝑓𝑓(𝑥𝑥)>𝑔𝑔(𝑥𝑥)
第 6页 /共 13页
学科网(北京)股份有限公司1.解:以社团甲中的人数为分类标准,则可分为两类:第一类是社团甲有 人,第二类是社团甲有
人.
3
当社团甲有 人时,可以分为 男 女和 男 女两种情况,
4
所以此时不同的参加方法有 种 ;
3 2 1 3 0
2 1 3
当社团甲有 人时,可以分为 𝐶𝐶4男 𝐶𝐶3 + 女 𝐶𝐶 、4 = 男 18 女 + 和 4= 男 22 女 ( 三 ) 种情况,
所以此时不同的参加方法有 种 .
4 2 2 3 1 4 0
2 2 3 1 4
由分类加法计数原理可得,
𝐶𝐶
满4足 𝐶𝐶3条
+
件 𝐶𝐶4的
𝐶𝐶
不3
+
同
𝐶𝐶
的4参
=
加
18
方
+
法
1
种
2+
数
1
是
=31( )
.
故选: .
22+31=53
分社团甲有 人和 人讨论即可.
𝐵𝐵
本题主要考查组合及简单的计数问题,考查运算求解能力,属于基础题.
3 4
2. 试题分析:因为, ,所以, ,而
,所以, , . ,
=0 𝑎𝑎 =−1 =
故选B。
考点:导数计算,二次函数的图象和性质。
点评:简单题,通过求函数的导数,并研究导函数的图象,确定得到 的取值,从而进一步确定得
到 。 𝑎𝑎
3. 解:根据题意,对于数列 , , , , ,
有 , , , , ,
1 3 7 13 21 …
2 2 2 2 2
归纳可得: .
1=1 −1+1 3=2 −2+1 7=3 −3+1 13=4 −4+1 21=4 −4+1
2
故选: . 𝑎𝑎𝑛𝑛 =𝑛𝑛 −𝑛𝑛+1
根据题意,归纳数列各项与 的关系,分析可得答案.
𝐶𝐶
本题考查数列的表示方法,涉及数列的通项公式,属于基础题.
𝑛𝑛
4. 解:某校高三年级有班号为 ~的 个班,
从这 个班中任抽 个班级参加一项活动,
1 9 9
基本事件总数 ,
9 5
5
抽出班级的班
𝑛𝑛
号
=
的
𝐶𝐶
中9位
=
数
12
是
6
包含的基本事件个数
2 2
抽出班级的班号的中位数是5 的概率 𝑚𝑚=.𝐶𝐶 4𝐶𝐶4 =36
𝑚𝑚 36 2
∴故选: . 5 𝑝𝑝= 𝑛𝑛 =126=7
𝐶𝐶
第 7页 /共 13页
学科网(北京)股份有限公司先求出基本事件总数 ,再求出抽出班级的班号的中位数是 包含的基本事件个数 ,
5 2 2
由此能求出抽出班级的 𝑛𝑛 = 班 𝐶𝐶 号9的中位数是 的概率. 5 𝑚𝑚 =𝐶𝐶4𝐶𝐶4
本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运
5
用.
5.
本题考查等差数列的性质及前 项和公式的应用,属于基础题目.
𝑛𝑛
解:由等差数列的性质可知,
在等差数列 中 , , 仍为等差数列,
所以 ,
− −
所以
2( −
.
)= + −
故选C= .
2 1
6.
本题考查独立性检验,属于较易题.
根据独立性检验思想可解.
解:根据题意,由公式可得 ,
2
2 110×(10×30−50×20)
且 . 𝜒𝜒 = 60×50×30×80 ≈7.486>6.635
有 的把握认为数学考试成绩与班级有关.
7.486<7.879
故选: .
∴ 99%
7. 𝐷𝐷
根据题意,先把 名大学生分成三组,一组 人,另两组都是 人,计算其分组的方法种数,进而将
三个组分到 个班,即进行全排列,计算可得答案.
5 1 2
本题考查排列、组合的运用,注意先要根据题意要求,进行分类讨论,其次要正确运用分组公
3
式.
解:将 名大学生分配到高一年级的 个班实习,每班至少 名,最多 名,
则将 名5大学生分成三组,一组 人,3另两组都是 人,有 1 种2方法,
2 2
𝐶𝐶5𝐶𝐶3
再将5组分到 个班,共有 1 种不同的分2配方案,𝐴𝐴 2 2 =15
3
故选 3 : . 3 15⋅𝐴𝐴3 =90
8. 𝐵𝐵
第 8页 /共 13页
学科网(北京)股份有限公司本题主要考查利用导数研究恒成立问题,属于中档题.
将题干不等式变形为 ,构造函数 ,利用函数 的单
𝑥𝑥 𝑥𝑥 2 2
调性将问题转化为 𝑒𝑒 +恒𝑥𝑥𝑛𝑛成 𝑒𝑒立⩾问𝑚𝑚题𝑥𝑥,令+𝑥𝑥𝑛𝑛 (𝑚𝑚𝑥𝑥 ),利用导数𝑓𝑓研(𝑥𝑥究)=函𝑥𝑥数+ln𝑥𝑥最值即可求解𝑓𝑓(.𝑥𝑥)
𝑥𝑥 𝑥𝑥
𝑒𝑒 𝑒𝑒
𝑥𝑥 2 ⩾𝑚𝑚 𝑔𝑔(𝑥𝑥)=𝑥𝑥 2 𝑔𝑔(𝑥𝑥)
解:由题意得, ,
𝑥𝑥 2 2
即 恒成立,
𝑒𝑒 +𝑥𝑥 ⩾𝑚𝑚𝑥𝑥 +𝑥𝑥𝑛𝑛(𝑚𝑚𝑥𝑥 )
𝑥𝑥 𝑥𝑥 2 2
令𝑒𝑒 +𝑥𝑥𝑛𝑛 𝑒𝑒 ⩾𝑚𝑚𝑥𝑥,因+为𝑥𝑥𝑛𝑛 (𝑚𝑚𝑥𝑥 ) ,
′ 1
所𝑓𝑓以(𝑥𝑥函)数=𝑥𝑥+在ln 𝑥𝑥 上𝑓𝑓单 (𝑥𝑥调)递=增1+, 𝑥𝑥 >0
则不等式转化为 ,所以 ,
𝑓𝑓(𝑥𝑥) (0,+∞)
𝑥𝑥 2 𝑥𝑥 2
则 对一切𝑓𝑓(𝑒𝑒 )⩾𝑓𝑓(𝑚𝑚恒𝑥𝑥成)立. 𝑒𝑒 ⩾𝑚𝑚𝑥𝑥
𝑥𝑥
𝑒𝑒
令𝑥𝑥 2 ⩾𝑚𝑚 ,则𝑥𝑥 ∈(0,+∞) ,
𝑥𝑥 𝑥𝑥
𝑒𝑒 ′ 𝑒𝑒 (𝑥𝑥−2)
则𝑔𝑔当(𝑥𝑥)=𝑥𝑥 2 时𝑔𝑔, (𝑥𝑥)= 𝑥𝑥 3, 单调递减;
′
当 时, , 单调递增,
0<𝑥𝑥 <2 𝑔𝑔 (𝑥𝑥)<0 𝑔𝑔(𝑥𝑥)
′
所以当 时, 有最小值,
𝑥𝑥 >2 𝑔𝑔 (𝑥𝑥)>0 𝑔𝑔(𝑥𝑥)
即 𝑥𝑥 =2 𝑔𝑔(𝑥𝑥) ,则 的最大值为 .
2 2
𝑒𝑒 𝑒𝑒
故𝑔𝑔选(𝑥𝑥B).mi n =𝑔𝑔(2)= 4 𝑚𝑚 4
9. 解:选项A,对于独立性检验 的值越大,说明这两事件具有相关性的把握越大,错误;
2
选项B, ~ , 𝑘𝑘 , ,正确;
2
选项C,𝜉𝜉~𝑁𝑁(1,𝜎𝜎 ,) 则𝑃𝑃(𝜉𝜉 ≤4)=0.75 ∴𝑃𝑃(𝜉𝜉 >4,)=𝑃𝑃(𝜉𝜉 ≤−2)=1−0.75=,0正.2确5 ;
1 1 1 2
选项D,𝑋𝑋把 𝐵𝐵(9,代3)入回归𝐷𝐷(直𝑋𝑋)线=方9程×3×(1−3)=,2得𝐷𝐷(2𝑋𝑋+1)=2 𝐷𝐷(𝑋𝑋),= 8
̂ −
剔除两个样𝑥𝑥本=点2 和 后,𝑦𝑦新=的2𝑥𝑥平−均0数.4 𝑦𝑦 =2×2−,0.4=3.6 ,
− −
2×10 3.6×10
又新的回归直线的(−斜3,1率)为(3,,−即1) ,则 𝑋𝑋 = 8 =2.5,𝑌𝑌解=得 8 =,4. 5
̂ ̂ ̂ ̂
则新的回归方程为 3 ,𝑦𝑦正=确3;𝑥𝑥 +𝑎𝑎 4.5=3×2.5+𝑎𝑎 𝑎𝑎 =−3
̂
故选: .
𝑦𝑦 =3𝑥𝑥−3
由独立
𝐵𝐵
性
𝐶𝐶
检
𝐷𝐷
验判断选项A,由正态分布的对称性,判断选项B,由二项分布的方差公式,判断选项
C,由回归直线方程的求法,判断选项D.
本题考查回归直线方程,独立性检验,二项分布的方差,正态曲线的性质,属于基础题.
第 9页 /共 13页
学科网(北京)股份有限公司10.
本题考查折线图,属于较难题.
根据图中给的折线图,对选项一一进行分析比较即可得到答案.
解:由图可知, 年 月比 年 月 上涨 %,故A不正确;
年 月比 20年19 月12 上涨2018%,12故𝐶𝐶B𝑃𝑃正𝐼𝐼确;4 .5
2 020
年
3
月至
2019
年
3
月
𝐶𝐶𝑃𝑃
的
𝐼𝐼
环比
4
均
.3
为正数,所以 持续增长,故C正确;
2019
年
7
月至
2019
年
1
月
1
的环比有正有负,所以
𝐶𝐶𝑃𝑃
有
𝐼𝐼
升有降,故D不正确.
故选:
2020 1 2020 3 𝐶𝐶𝑃𝑃𝐼𝐼
11. 𝐵𝐵 𝐶𝐶
对于 根据杨辉三角的特点结合不等式性质可判定正确,对于 第 行的第 个数等于第 行的第一
个数和第 行的第一个数相乘,所以正确,对于 直接根据每一行距离首位距离相等的两项相
𝐴𝐴 𝐵𝐵 𝑛𝑛 2 𝑛𝑛
等求解即可,对于 根据每一个数均等于其“脚下”两个数之和判断即可.
𝑛𝑛−1 𝐶𝐶
本题主要考查了对杨辉三角定义的应用,组合数的性质,考查了逻辑推理能力和运算求解能力,
𝐷𝐷
是中档题.
解:对于 ,根据杨辉三角的特点,当 为偶数时,中间的一项取得最大值;当 为奇数时,中间的
两项相等,且同时取得最大值,
𝐴𝐴 𝑛𝑛 𝑛𝑛
当每一项取倒数时,再乘以一个常数,可得当 是偶数时,中间的一项取得最小值;当 时奇数
时,中间的两项相等,且同时取得最小值,所以 不正确,
𝑛𝑛 𝑛𝑛
对于 ,第 行第 个数是 所以B正确𝐴𝐴,
1 1
对于 𝐵𝐵 ,每一 8 行距 2 离首位距(8+离1)相𝐶𝐶8 1 等 = 的72两项相等,即 ,所以
1 1
𝐶𝐶 𝑛𝑛−𝐶𝐶
𝐶𝐶 ,所以C正确, (𝑛𝑛+1)𝐶𝐶𝑛𝑛 =(𝑛𝑛+1)𝐶𝐶𝑛𝑛 (𝐶𝐶 ∈𝑁𝑁,0≤𝐶𝐶 ≤𝑛𝑛)
𝑟𝑟 𝑛𝑛−𝑟𝑟
𝐶𝐶对𝑛𝑛于=𝐶𝐶,𝑛𝑛 开始每个数均等于其“脚下”两个数之和,即
1 1 1
,𝐷𝐷所以D错误,
(𝑛𝑛+1)𝐶𝐶𝑛𝑛
𝐶𝐶−1+(𝑛𝑛+1)𝐶𝐶𝑛𝑛 𝐶𝐶 =
𝑛𝑛𝐶𝐶𝑛𝑛
𝐶𝐶−
−
1
1
(𝐶𝐶 ∈𝑁𝑁,1≤𝐶𝐶 ≤
所以关于莱布尼茨三角形的性质描述正确的是 .
𝑛𝑛)
故选BC
𝐵𝐵𝐶𝐶
12. 解: , ,
6 7
令 , ∵ 则 (1+𝑥𝑥)(𝑎𝑎−𝑥𝑥) =𝑎𝑎0+𝑎𝑎1𝑥𝑥+⋯+𝑎𝑎 ,7𝑥𝑥 𝑎𝑎0+𝑎𝑎1+⋯+𝑎𝑎7 =0
6
解 𝑥𝑥 得 =1 . 2 (𝑎𝑎−1) =𝑎𝑎0+𝑎𝑎1+⋯+𝑎𝑎7 =0
𝑎𝑎 =1 第 10页 /共 13页
学科网(北京)股份有限公司.
6 6
的通项公式 ,
∴(1+𝑥𝑥)(𝑎𝑎−𝑥𝑥) =(1+𝑥𝑥)(1−𝑥𝑥)
6 𝑟𝑟 𝑟𝑟
( 令 1−𝑥𝑥) 或 , 𝑇𝑇𝑟𝑟+1 =∁6(−𝑥𝑥)
则 .
𝐶𝐶 =3 𝐶𝐶 =2
3 2
故答 𝑎𝑎3案 = 为 − : ∁6+∁ .6= −5
, ,令 ,可得
−5
6 7 6
(1+𝑥𝑥)(𝑎𝑎−𝑥𝑥) , = 解 𝑎𝑎0得 +𝑎𝑎1再 𝑥𝑥 利 + 用 ⋯ 通 + 项 𝑎𝑎7公 𝑥𝑥 式即 𝑎𝑎0可 + 得 𝑎𝑎1出 + . ⋯ +𝑎𝑎7 =0 𝑥𝑥 =1 2(𝑎𝑎−1) =𝑎𝑎0+
𝑎𝑎
本1题
+
考
⋯
查
+
了 𝑎𝑎7二
=
项
0
式定理的
𝑎𝑎.
应用、方程的解法,考查了推理能力与计算能力,属于基础题.
13. 解:因为 ~ , , ,
2
所以 ,
𝑋𝑋 𝑁𝑁(1.4,0.05 ) 𝜇𝜇 =1.4 𝜎𝜎 =0.05
即 落在区间 中的概率为 .
𝑃𝑃(𝜇𝜇−𝜎𝜎 <𝑋𝑋 <𝜇𝜇+𝜎𝜎)=𝑃𝑃(1.4−0.05<𝑥𝑥 <1.4+0.05)=0.683
故答案为: .
𝑋𝑋 (1.35,1.45) 0.683
根据正态分布的 原则,计算即可.
0.683
本题考查正态分布的运用,属于基础题.
3𝜎𝜎
14.
本题考查考查导数的几何意义,导数中的存在性问题,注意运用转化思想,以及构造函数法,考
查运算能力,属于中档题.
求得 的导数,由题意可得 无实数解,即有 ,设 ,求得导数
𝑥𝑥 𝑥𝑥
′ 𝑥𝑥 𝑒𝑒 𝑒𝑒
和单𝑓𝑓调(区𝑥𝑥)间,求得极小值,结𝑓𝑓合(图𝑥𝑥)象=即𝑎𝑎可𝑥𝑥−得𝑒𝑒到=的0范围. 𝑎𝑎 = 𝑥𝑥 𝑔𝑔(𝑥𝑥)= 𝑥𝑥
𝑎𝑎
解: 的导数为 ,
𝑎𝑎 2 𝑥𝑥 ′ 𝑥𝑥
由 𝑓𝑓(不𝑥𝑥)存=在 2𝑥𝑥垂直−于𝑒𝑒 轴的切线𝑓𝑓,(𝑥𝑥 )=𝑎𝑎𝑥𝑥−𝑒𝑒
可得 无实数解,
𝑓𝑓(𝑥𝑥) 𝑦𝑦
𝑥𝑥
由 𝑎𝑎𝑥𝑥−,𝑒𝑒设=0 ,
𝑥𝑥 𝑥𝑥
𝑒𝑒 𝑒𝑒
可𝑎𝑎得= 𝑥𝑥 𝑔𝑔(𝑥𝑥)=,𝑥𝑥
𝑥𝑥
′ 𝑒𝑒 (𝑥𝑥−1)
当 𝑔𝑔 (𝑥𝑥时),= 𝑥𝑥 2 , 在 单调递增;
′
当 或 时, , 在 , 单调递减.
𝑥𝑥 >1 𝑔𝑔 (𝑥𝑥)>0 𝑔𝑔(𝑥𝑥) (1,+∞)
′
即有 在 处取得极小值,且为 ,
𝑥𝑥 <0 0<𝑥𝑥 <1 𝑔𝑔 (𝑥𝑥)<0 𝑔𝑔(𝑥𝑥) (−∞,0) (0,1)
由于直线 与 图象无交点,
𝑔𝑔(𝑥𝑥) 𝑥𝑥 =1 𝑒𝑒
可得 ,
𝑦𝑦 =𝑎𝑎 𝑦𝑦 =𝑔𝑔(𝑥𝑥)
0≤𝑎𝑎 <𝑒𝑒
第 11页 /共 13页
学科网(北京)股份有限公司故答案为: .
[0,𝑒𝑒)
15. 由题意得 ,解得 的值;
𝜋𝜋 1 2
求(1导),利用导𝑆𝑆数=法∫分0 析𝑓𝑓(函𝑥𝑥)数𝑎𝑎𝑥𝑥的=单
2
调𝜋𝜋性+,𝜋𝜋进+而2可得函𝑎𝑎数 单调区间及最值;
作出函数 , 的简图,数形结合可得函数
(2) 𝑓𝑓(𝑥𝑥)
在区间 上的零点个数.
(3) 𝑓𝑓(𝑥𝑥)=𝐶𝐶𝑖𝑖𝑛𝑛𝑥𝑥−𝑏𝑏𝐶𝐶𝐶𝐶𝑥𝑥+𝑥𝑥+1 𝑥𝑥 ∈[0,2𝜋𝜋] 𝑔𝑔(𝑥𝑥)=𝑓𝑓(𝑥𝑥)−𝑚𝑚
本题考查的知识点是定积分,利用导数研究函数的单调性,利用导数研究函数的最值,函数的零
𝑥𝑥 ∈[0,2𝜋𝜋]
点,难度中档.
16. 本题考查二项式定理的应用以及二项展开式的特定项的系数和利用导数研究函数单调性、和基
本不等式的应用,属于难题.
展开式中二项式系数最大的项是第 项和第 项,求解即可;
1 5
(1)灵(1活+使 𝑛𝑛)用均值不等式进行放缩来证明; 3 4
(2)多次放缩,最后得到 ,从而最后得到 的值.
𝑚𝑚
1
(137). 借助二进制的定义2<计�算1可+得𝑚𝑚� <3 ,𝑎𝑎 ,即可得证;
借助二进制的定义可计算出 ,即可得表达式中的 的个数; 计算出从 到
(1) 𝑆𝑆(16𝑛𝑛+3)=𝑆𝑆(𝑛𝑛)+2 𝑆𝑆(4𝑛𝑛+3)=𝑆𝑆(𝑛𝑛)+2
中, 、 、 , 的个数,即可求解.
(2)(𝑖𝑖) 80 0 (𝑖𝑖𝑖𝑖) 𝑛𝑛 =1 𝑛𝑛 =255
本题考查进位制、数列的综合应用,属于难题.
𝐼𝐼(𝑛𝑛)=0 𝐼𝐼(𝑛𝑛)=1 … 𝐼𝐼(𝑛𝑛)=7
18. 根据全概率公式、条件概率计算公式求得正确答案.
根据独立重复事件概率计算公式求得 .
(1)
先求得 的表达式,根据极限的知识证得结论成立.
(2) 𝐻𝐻
本题考查离散型随机变量的期望与方差,属于难题.
(3) 𝐸𝐸(𝑌𝑌)
19. 本题考查了导数的几何意义、利用导数研究函数的极值和利用导数证明不等式,是较难题.
先求导,代入切点横坐标得出切线斜率,进而得出切线方程;
(1)
第 12页 /共 13页
学科网(北京)股份有限公司先求导,利用导数研究单调性,可得函数的极值点个数;
令 ,令 ,利用导数研究单调性和最值,即可得证.
(2)
(3) 𝐹𝐹(𝑥𝑥)=𝑥𝑥ln𝑥𝑥+1−𝑥𝑥 𝐺𝐺(𝑥𝑥)=𝑥𝑥−sin𝑥𝑥
第 13页 /共 13页
学科网(北京)股份有限公司