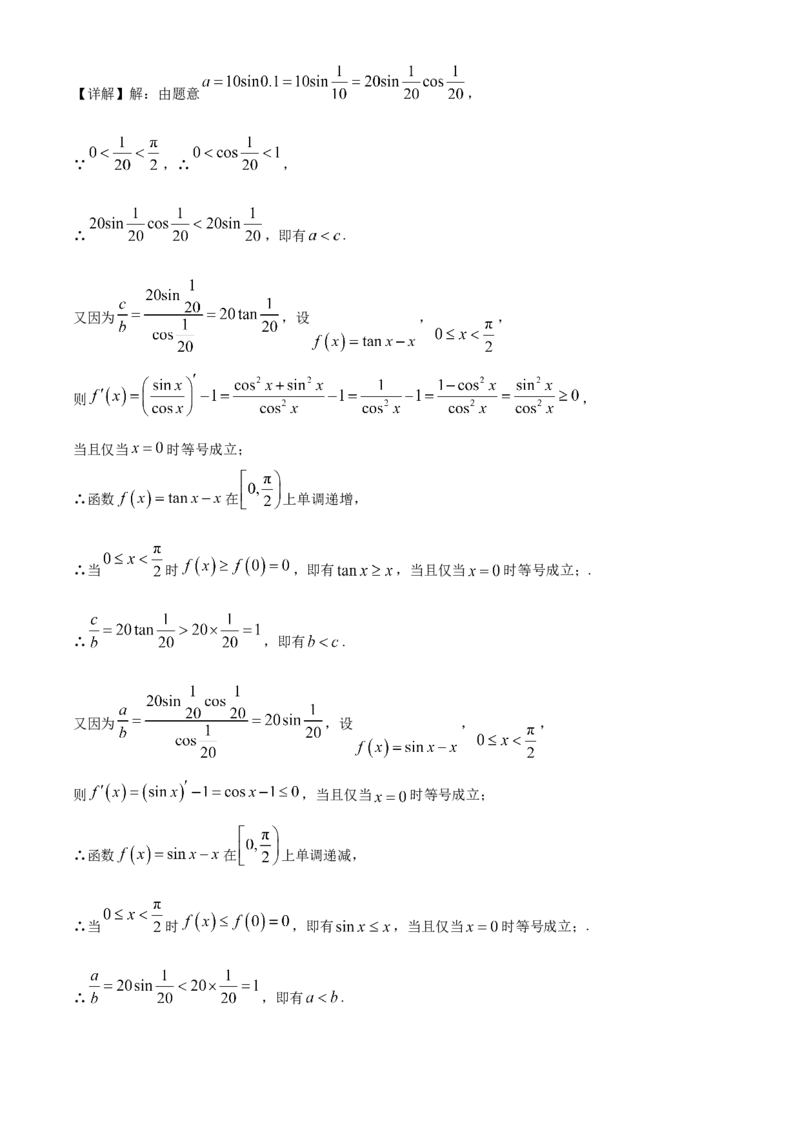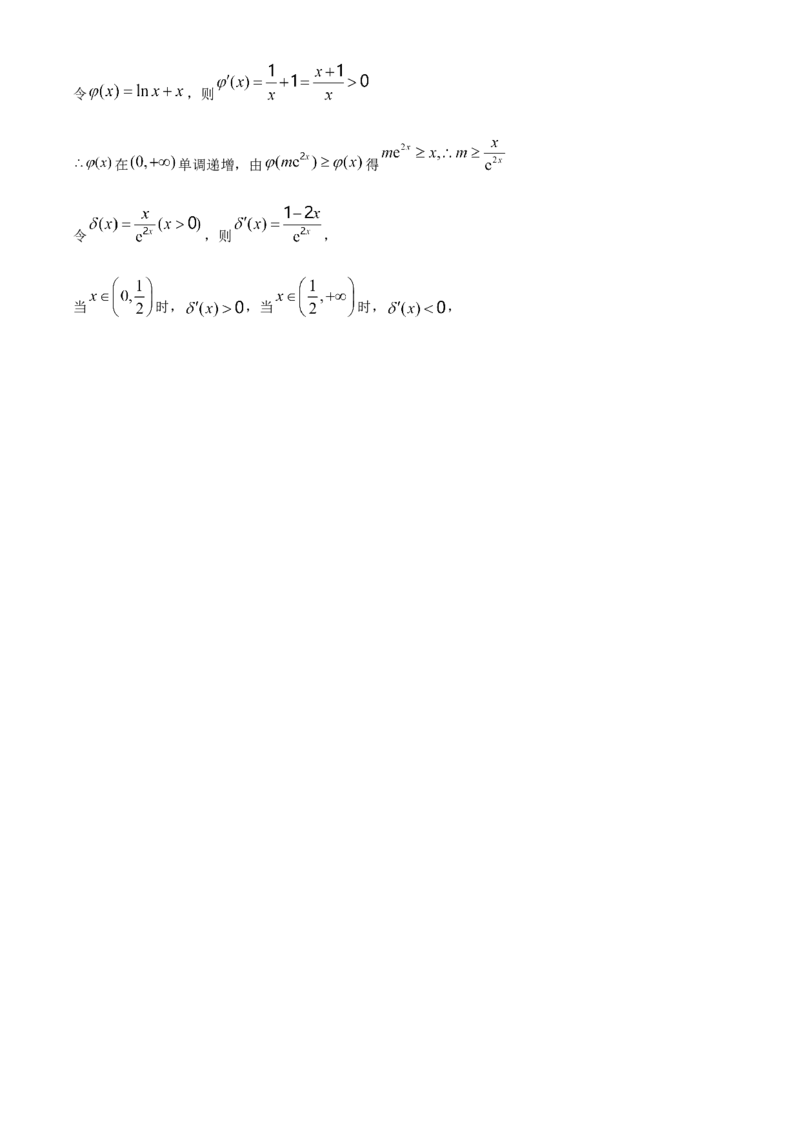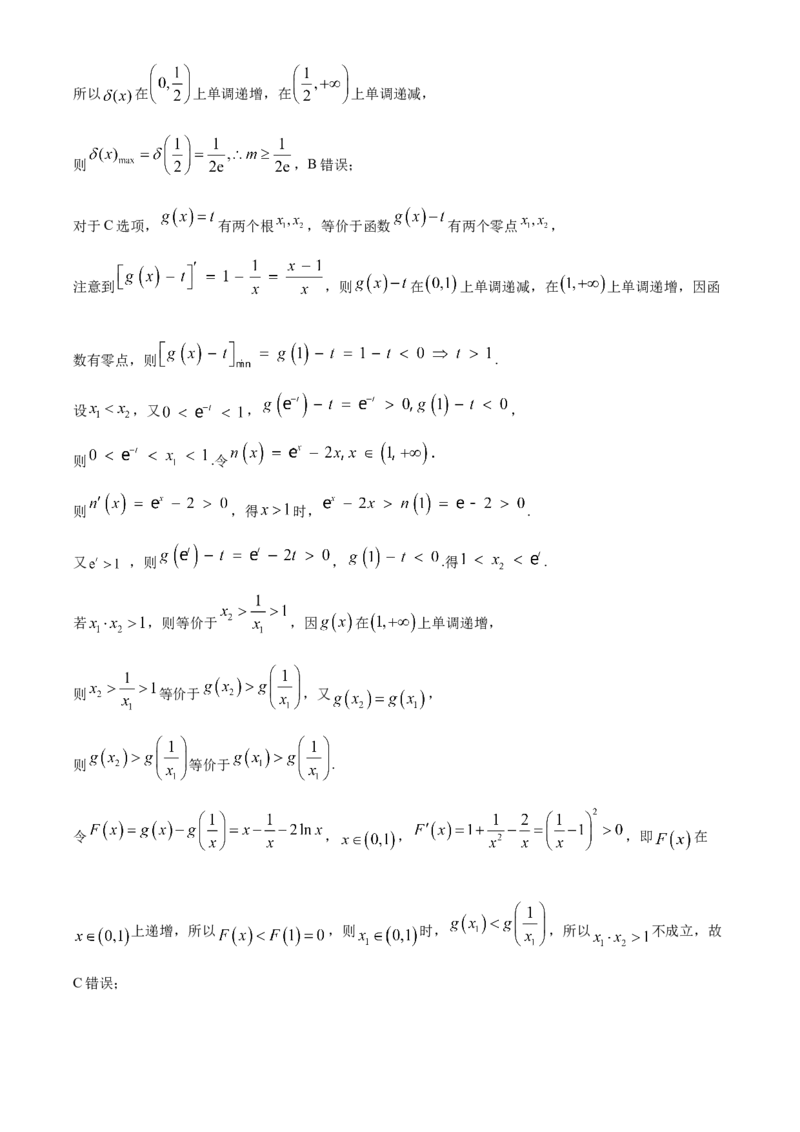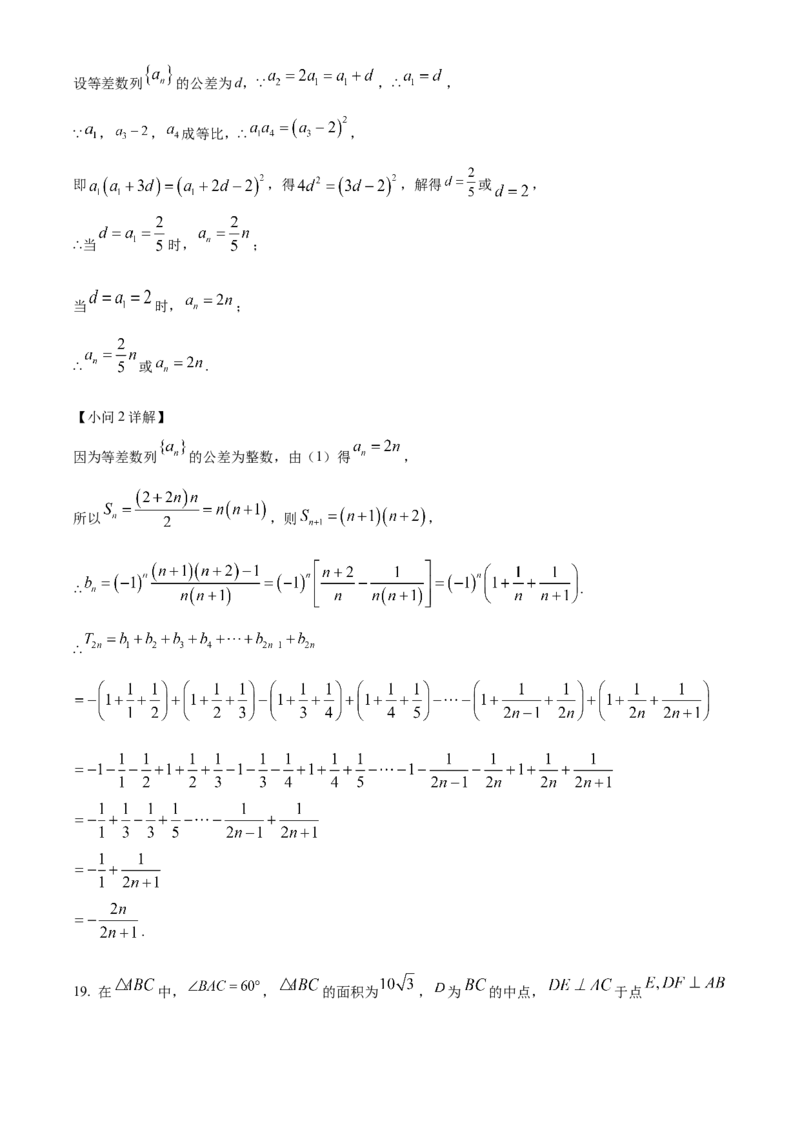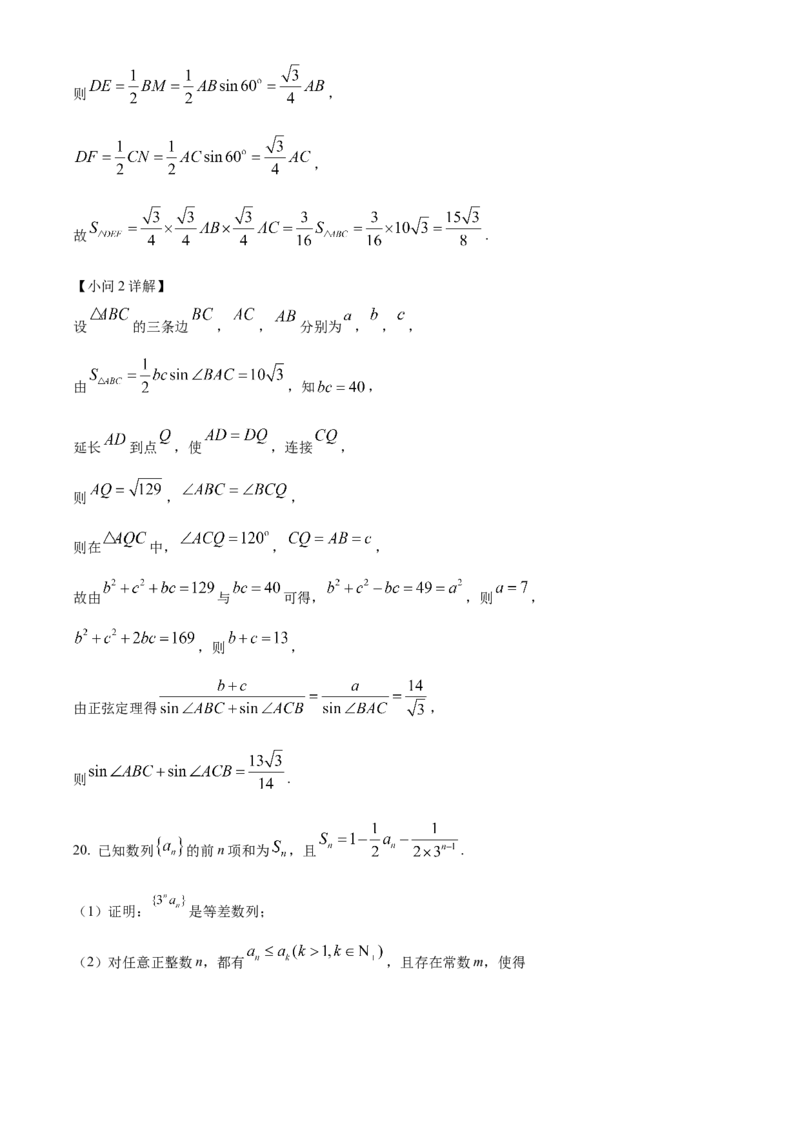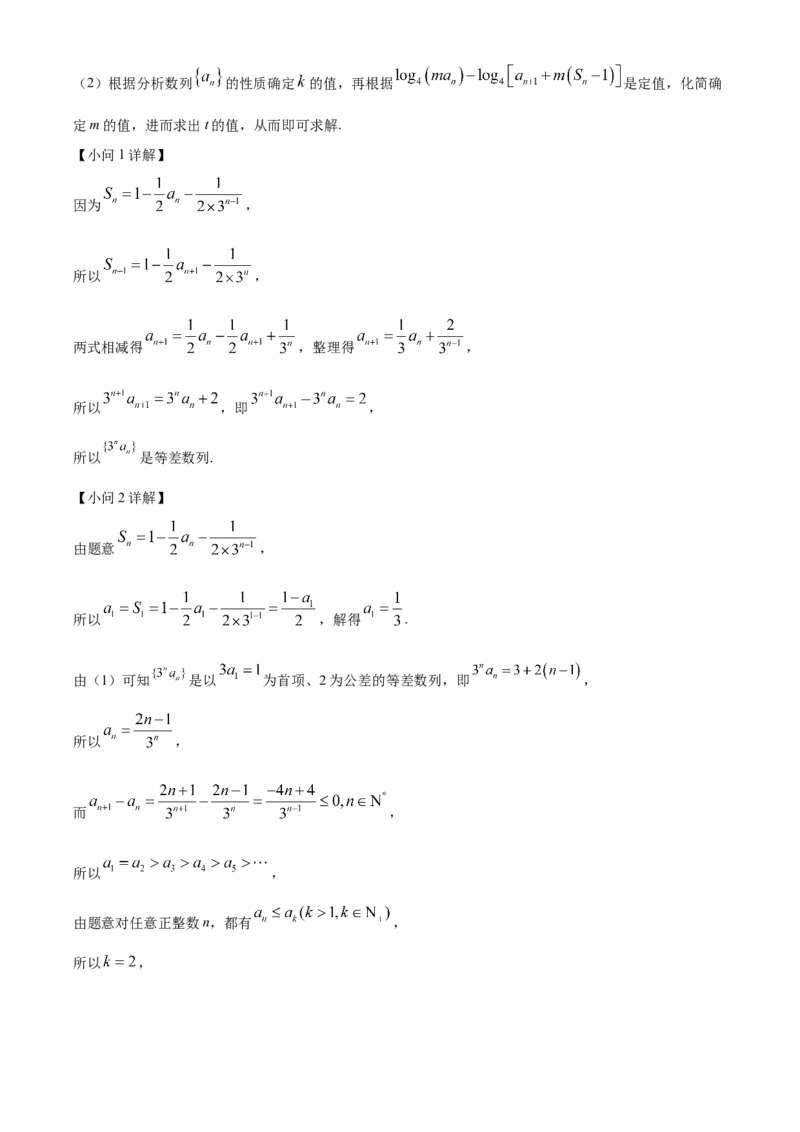精品解析：黑龙江省大庆实验中学2023-2024学年高三上学期期中考试数学试题（解析版）(1)_2023年11月_0211月合集_2024届黑龙江省大庆实验中学高三上学期期中考试

大庆实验中学 2023——2024 学年度第一学期高三期中考试 数学试题 第Ⅰ卷(选择题，共60分) 一、单项选择题：本大题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只 有一个符合题目要求. 1. 已知集合 ，则 （ ） A. B. C. D. 【答案】A 【解析】 【分析】化简集合 ,即可由并运算求解. 【详解】由 得 ， ， 所以 ， 故选：A 2. 已知平面向量 ， 满足 ，且 ， ，则 （ ） A. B. C. D. 1 【答案】D 【解析】 【分析】根据向量数量积可得 ，再由 即可得出 . 【详解】由 可得 ， 又 可得 ，所以 ； 即 ，所以 . 故选：D 3. 南宋数学家杨辉在《详解九章算术》中提出了高阶等差数列的问题，即一个数列 本身不是等差数列但从 数列中的第二项开始，每一项与前一项的差构成等差数列 （则称数列 为一阶等差数 列），或者 仍旧不是等差数列，但从 数列中的第二项开始，每一项与前一项的差构成等差数列（则称数列 为二阶等差数列），依次类推，可以得到高阶等差数列．类比高阶等差数列的定义，我们 亦可定义高阶等比数列，设数列 是一阶等比数列，则该数列的第 项是（ ） A. B. C. D. 【答案】C 【解析】 【分析】根据数列特征可知数列 为等比数列，进而得到 ，利用累乘法可求得 ，代入 即可. 【详解】记数列 为 ，设 ， 则 ， ， ， ， ， 数列 是以 为首项， 为公比的等比数列， ， ， . 故选：C. 4. 已知 ，则 （ ） A. B. C. D. 【答案】D 【解析】 【分析】根据三角恒等变换得到 ，再利用诱导公式求出答案. 【 详 解 】 因 ， 即 为 ，所以 ． 故选：D 5. 已知函数 若方程 有4个不同的零点 ，且，则 （ ） A. 10 B. 8 C. 6 D. 4 【答案】A 【解析】 【分析】利用函数图象、对数的运算性质和二次函数的图象与性质分析运算即可得解. 【详解】解：由题意，方程 有4个不同的零点，即 曲线 与直线 有4个不同的交点，如下图 因为 ，所以由图知 ， 且 ，可得： ，∴ ， 解得： ，则 ， ∴ . 故选：A. . 6 设 ，则（ ） A. B. C. D.【答案】D 【解析】 【分析】构造函数，根据三角函数的性质、利用导数判断单调性，作商比较大小即可得解.【详解】解：由题意 ， ∵ ，∴ ， ∴ ，即有 . 又因为 ，设 ， ， 则 ， 当且仅当 时等号成立； ∴函数 在 上单调递增， ∴当 时 ，即有 ，当且仅当 时等号成立；. ∴ ，即有 . 又因为 ，设 ， ， 则 ，当且仅当 时等号成立； ∴函数 在 上单调递减， ∴当 时 ，即有 ，当且仅当 时等号成立；. ∴ ，即有 .综上知， . 故选：D. 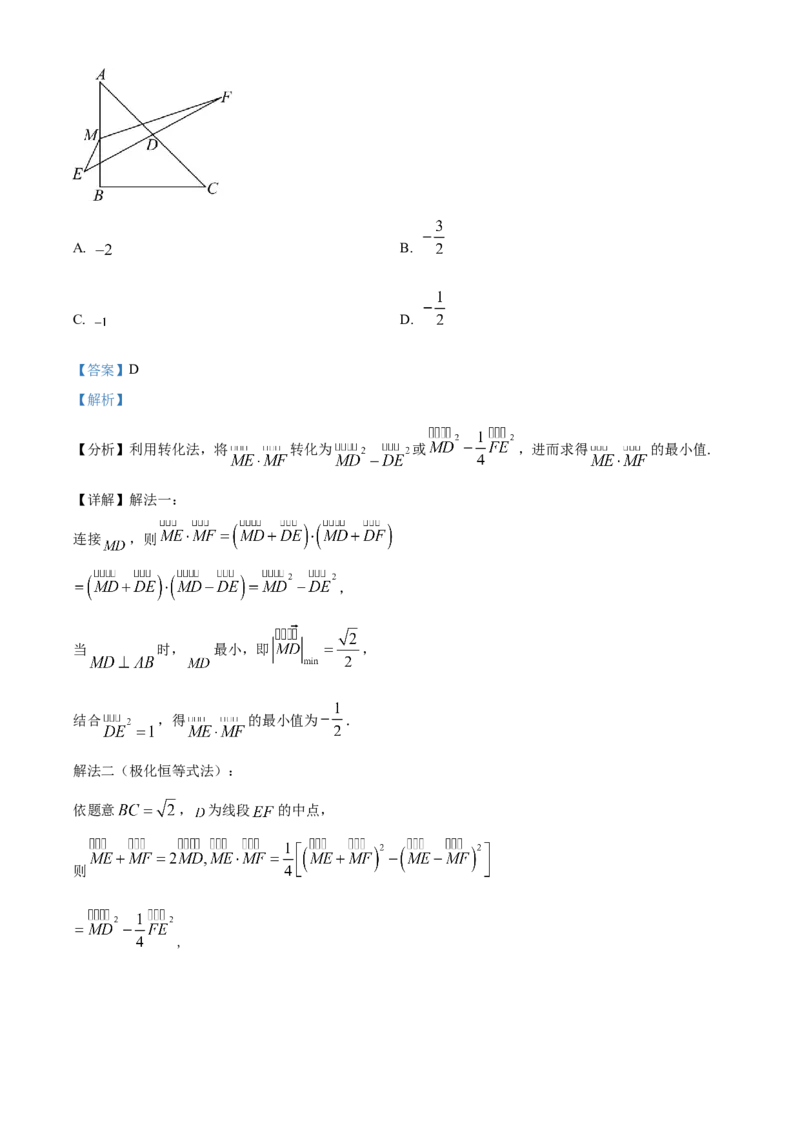7. 如图，在等腰直角三角形 中，斜边 ， 为线段 上的动点（包含端点）， 为 的 中点．将线段 绕着点 旋转得到线段 ，则 的最小值为（ ）A. B. C. D. 【答案】D 【解析】 【分析】利用转化法，将 转化为 或 ，进而求得 的最小值. 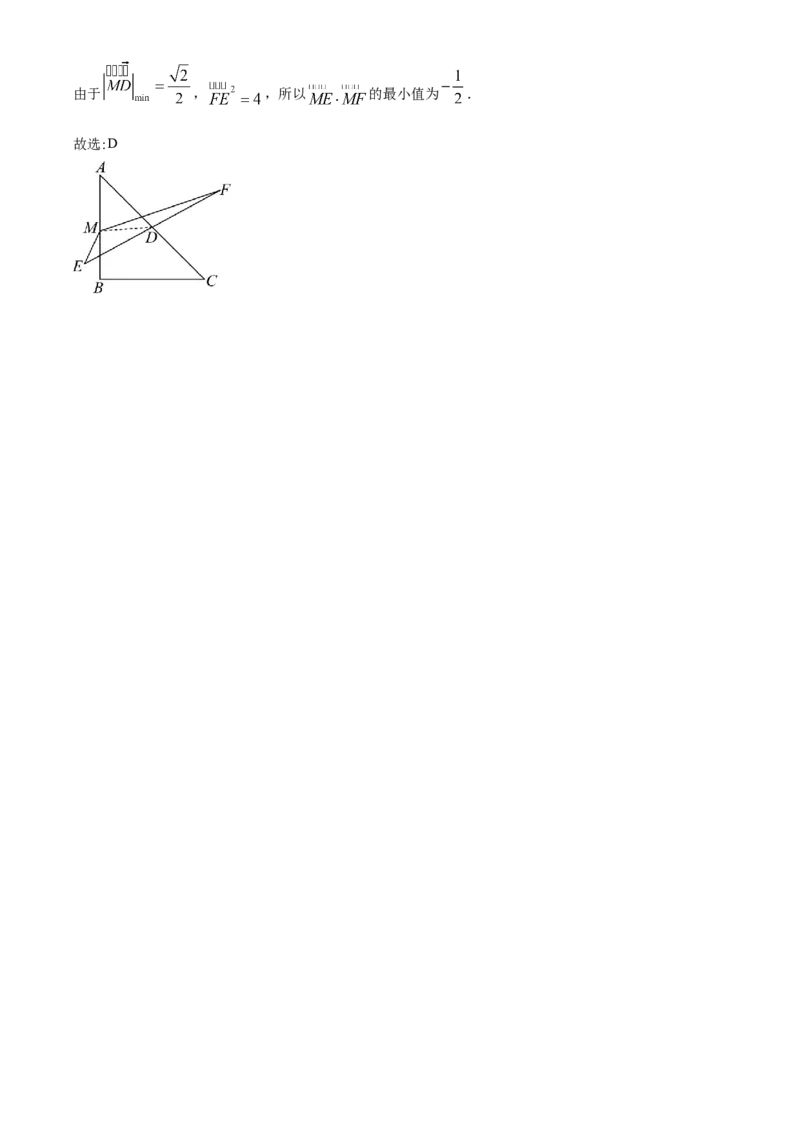【详解】解法一： 连接 ，则 ， 当 时， 最小，即 ， 结合 ，得 的最小值为 ． 解法二（极化恒等式法）： 依题意 ， 为线段 的中点， 则 ,由于 ， ，所以 的最小值为 ． 故选:D8. 已知函数 的定义域为R，且 ， 为奇函数， ，则 （ ） A. B. C. 0 D. 【答案】B 【解析】 【分析】根据 即可得出 周期为4，赋值可求出 .进而由 为奇函数，可推得函数 关于点 对称，由已知可求出 ， ， ， 然后即可求得 ， .进而即可根据周期性得出函数值，求出 ，即可得出 ，代入数值，即可得出答案. 【详解】由 ，则 ， 所以， ， 周期为4，所以 . 由 ，令 ，则有 ，所以， . 因为 为奇函数，所以 ， 所以， ，所以函数 关于点 对称，所以， . 令 ，则 . 令 可得， ，所以 ，所以 ， 所以，有 ，即有 .令 ，则有 ； 令 ，则 . 综上， ， ， ， . 所以， ， 所以， . 故选：B. 【点睛】方法点睛：抽象函数求解函数值，常用赋值法.根据已知关系，推得函数的周期以及对称性，根据 已知函数值，赋值求出其他函数值. 二、多项选择题：本大题共4小题，每小题5分，共20分，在每小题给出的四个选项中，至 少有一个符合题目要求，每道题全对得5分，部分选对得2分. 9. 已知复数 ，则（ ） A. 是纯虚数 B. 对应的点位于第二象限 C. D. 【答案】AD 【解析】 【分析】根据复数的运算规则和几何意义逐项分析.【详解】对于A， ，实部为0，是纯虚数，正确； 对于B， ，在复平面上对应点 ，在第四象限，错误； 对C， ，错误；对于D， ，正确； 故选：AD. 10. 已知等差数列 的公差为 ，前 项和为 ， ， ， ，则（ ） A. ， B. 的 C. ， 最大值为14 D. 当 时， 有最大值 【答案】ACD 【解析】 【分析】根据 ， ，得出 ，再逐一对各个选项分析判断，即可求出结果. 【详解】因为 ， ，故 ，故选项A正确； 选项B，因为 ， ，又 ，即 ，故选项B错误； 选项C，因为 ， ，又由 ，得到 ，所以 ，故选项C正确； 选项D，因为 ， ， ，故选项D正确. 故选：ACD. 11. 已知函数 ， ， ，( ) A. 若 在区间 上单调递减，则 B. 将函数 的图像向左平移 个单位得到曲线 ，若曲线 对应的函数为偶函数，则 的最小 值为C. 若方程 在区间 上恰有三个解，则 D. 关于 的方程 在 上有两个不同的解，则 【答案】BC 【解析】【分析】选项A：求出 单调递减满足的关系与选项比较即可；选项 B：平移后初相应为 的奇数倍； 选项CD：求出相位满足的范围，卡右端点的范围即可. 【详解】选项A： 时， ， 若 在区间 上单调递减，则 ， ， 解得 ， 因 ， ，所以 ， 进而得 ，故A错误； 选项B：函数 的图像向左平移 个单位得到 ， 若 为偶函数，则有 ， ，解得 ， ， 因为 ，所以 的最小值为 ，故B正确； 选项C： ， ，则 ， 解得 ，则C正确； 选项D： ，即 ， ， ，则 ，解得 ，故D错误， 故选：BC. 12. 已知函数 ，则下列说法正确的是( ) A. 在 上是增函数 B. 若不等式 恒成立，则正数m的取值范围是C. 若 有两个根 ，则 D. 若 ，且 ，则 的最大值为 【答案】A 【解析】 【分析】A选项，由题 ， ，判断 在 上的单调性即可； B选项，由 ，得 ，构造函数 ，求出其单 调性，得 ，再次构造函数 ，求出其最大值即可; C选项，由 有两个零点 ，可得 ，设 ，则 ，又 ，后研究 在 上的单调性 即可； D选项，因 ，及 在 上单调递增， 可得 . 又 ，则 ， 故 ，再次构造函数 ，求出最大值可判断选项. 【详解】对于A选项， ， . 又当 时， ，则 在 上是增函数，故A正确； 对于B选项， ，即 ，令 ，则 在 单调递增，由 得 令 ，则 ， 当 时， ，当 时， ，所以 在 上单调递增，在 上单调递减， 则 ，B错误； 对于C选项， 有两个根 ，等价于函数 有两个零点 ， 注意到 ，则 在 上单调递减，在 上单调递增，因函 数有零点，则 . 设 ，又 ， ， 则 .令 则 ，得 时， . 又 ，则 ， .得 . 若 ，则等价于 ，因 在 上单调递增， 则 等价于 ，又 ， 则 等价于 . 令 ， ， ，即 在 上递增，所以 ，则 时， ，所以 不成立，故 C错误；对于D选项，由A选项分析可知， 在 上单调递增， ， ，当 时 ， 则 在 单调递增， 又 ， ，则 .由 ，即 ，即有 ， 又 ， 在 上单调递增，所以 ，即 ，所以 ，其中 .令 ， ， 则 ，令 ，得 ，当 时， ， 当 时， ，所以 在 单调递增，在 单调递减， 所以 ，故D错误. 故选：A 【点睛】本题涉及求函数单调区间，恒成立问题及双变量问题，难度较大.对于复杂函数，常利用导数求单 调区间.对于恒成立问题，求解的关键是能够利用同构法,将恒成立的不等式转化为同一函数不同函数值的 大小关系比较问题,进而通过构造函数,利用函数单调性得到自变量的大小关系,从而化简恒成立的不等式， 常利用分离参数法将问题转化为求最值.对于双变量问题，常结合题目条件寻找变量间关系，将双变量转化 为单变量. 第Ⅱ卷(非选择题，共90分) 三、填空题：本题共4小题，每空5分，共20分.把答案填在答题卡的相应位置. 13. 已知球 的表面积为 ，平面 截球 所得的截面面积为 ，则以 为顶点，截面为底面的圆锥 的体积为__________． 【答案】 【解析】 【分析】根据球的表面积和截面圆面积可求得 ，利用勾股定理可求得球心 到截面的距离，代入圆 锥体积公式即可. 【详解】设球 的半径为 ，截面圆 的半径为 ，球心 到平面 的距离为 ，， ， ， ， ， 以 为顶点，截面为底面的圆锥的体积为 . 故答案为： .14. 已知 ， ，且 ，则 的最小值是______． 【答案】18 【解析】 【分析】利用基本不等式“1”的妙用求解最小值. 【详解】由题意可得 ，当且仅当 ， 时，等号 成立． 故答案为：18 15. 已知数列 和 ，其中 是 的小数点后的第 位数字，(例如 )，若 ，且对任意的 ，均有 ，则满足 的所有 的值为 _______． 【答案】 或 ## 或 【解析】 【分析】据题意可推导出 为周期数列，再分析可知 ，然后利用周期逐一验证数列 的各项与 计算结果是否一致，即可找到所有符合题意的 的值. 【详解】 是 的小数点后的第 位数字，且 . 是以3为周期的数列，且各项为 依次循环出现. 又 , 当 时， ，与数列 各项均为正数相矛盾； 当 时， 不符合题意，与数列 中最大项为 相矛盾；且 ， ， 与 相矛盾，故舍去； ，符合题意； 与 相矛盾，故舍去；，符合题意； 综上所述：对任意的 ，均有 ，则满足 的所有 的值为 或 . 故答案为： 或 16. 在 中，内角A，B，C所对的边分别为a，b，c，已知角A为最小角且 均为整 数，则 ___________，设 ， 的中点为D，则 ___________. 【答案】 ①. ②. 【解析】 【分析】对于第一空，因为A为最小角且 均为整数，可确定 ，故可得答案； 第二空，结合第一空的结果，根据 ， 均为整数，可确定 ，进而求得 ，然后利用正弦定 理即可表示边b,c，在 中由余弦定理表示出 ,即可求得答案. 【详解】第一空：在 中，A为最小角且 均为整数， 则 , 若 ，因为 ，且 在 上单调递增， 故 ，又因为A为最小角，则B,C都大于 ，与 矛盾， 所以 ，即 ； 第二空：由第一空可知 ，故 ，则 ，即 ， 因为 且 均为整数，故 , 为锐角， 故 , 由正弦定理得： ，即 ， 所以在 中， 的中点为D ，故 ， 则 ， 故 ； 故答案为： ； 四、解答题：本大题共6小题，其中17题满分10分，其余各题满分12分，共70分.把答案 填在答题卡的相应位置. 17. 已知函数 ， . （1）当 时，求曲线 在点 处的切线方程； （2）试讨论函数 的单调性. 【答案】（1） （2）答案见解析 【解析】 【分析】（1）先求函数的导函数得出斜率，再根据点斜式求出切线方程即可； （2）分 和 两种情况求导函数，分导数正负讨论函数的单调性. 【小问1详解】因为 ， 所以 ，则 ，切点为又因为 所以 ，即 所以曲线 在点 处的切线方程是 ， 即 . 【小问2详解】 因为 ， ， 所以 ， 当 时， ，则 在 上单调递减； 当 时，令 ，得 ， 当 时， ，当 时， ， 所以 在 上单调递减，在 上单调递增， 综上，当 时， 在 上单调递减； 当 时， 在 上单调递减，在 上单调递增 18. 已知等差数列 满足 ，且 ， ， 成等比数列. （1）求 的通项公式； （2）设 ， 的前n项和分别为 ， .若 的公差为整数，且 ，求 . 【答案】（1） 或 （2） 【解析】【分析】（1）根据题意，利用等差数列的通项公式和等比中项的应用求出 ，即可求出 ； （2）根据题意，由（1）可得 ，根据等差数列前 n 项求和公式计算可得 ，则 ，利用裂项相消求和法计算即可求解. 【小问1详解】设等差数列 的公差为d，∵ ，∴ ， ∵ ， ， 成等比，∴ ， 即 ，得 ，解得 或 ， ∴当 时， ； 当 时， ； ∴ 或 . 【小问2详解】 因为等差数列 的公差为整数，由（1）得 ， 所以 ，则 ， ∴ . ∴ . 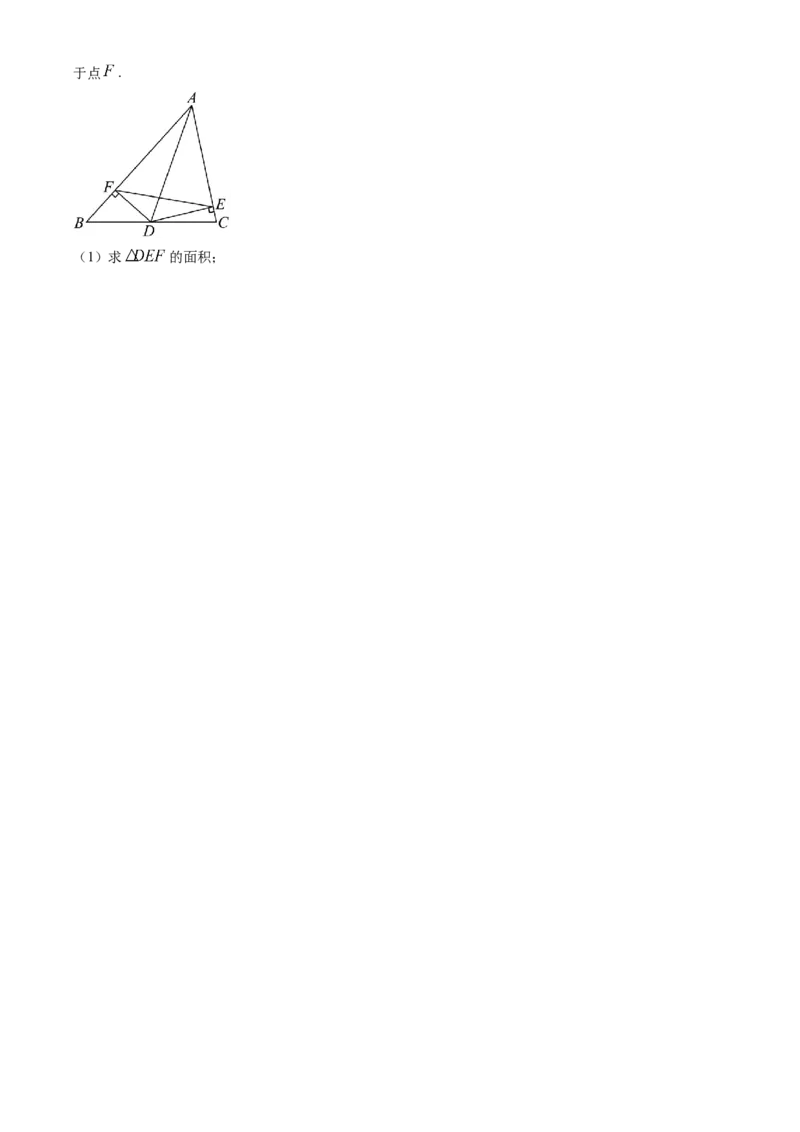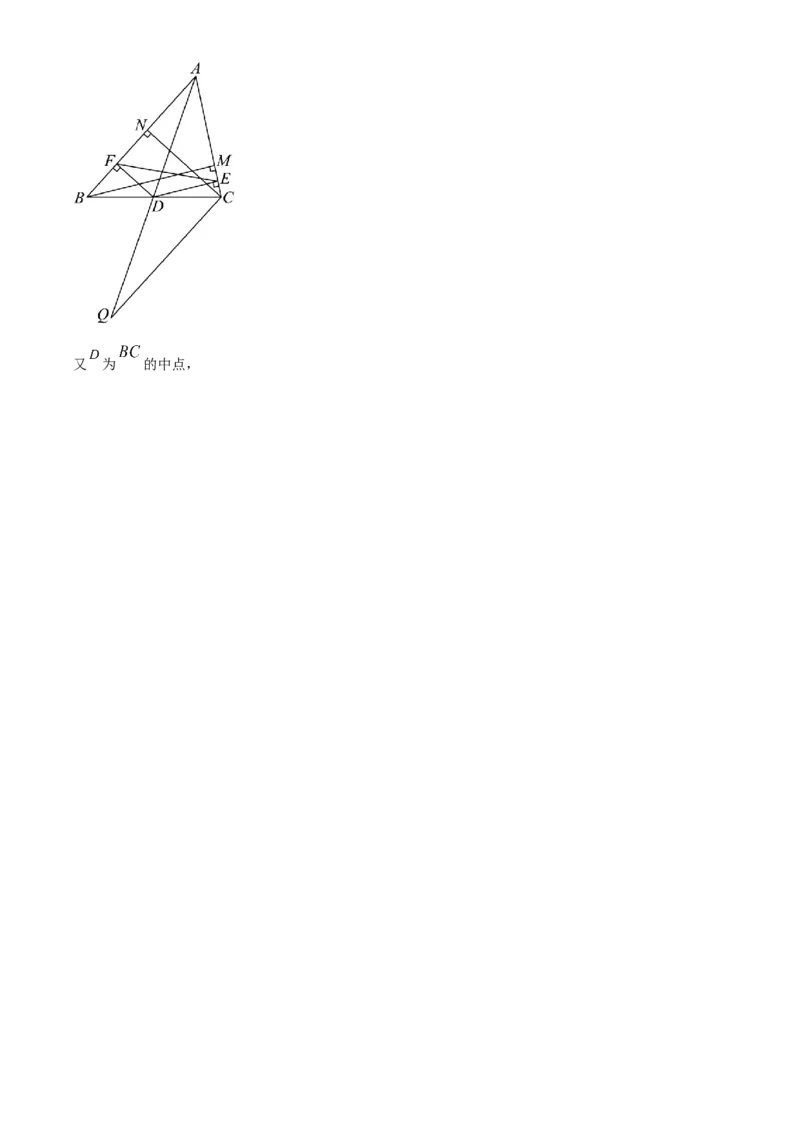19. 在 中， ， 的面积为 ， 为 的中点， 于点于点 . （1）求 的面积；（2）若 ，求 的值. 【答案】（1） （2） 【解析】 【 分 析 】 （ 1 ） 由 题 意 ， 可 得 ， ， 作 于点 ， 于点 ，可得 ， ，代入上 式得解； （2）延长 到点 ，使 ，连接 ，在 中，利用余弦定理可得 ，在 中由 正弦定理可求得结果. 【小问1详解】 在四边形 中， ， ， 故 ， 故 ， 作 于点 ， 于点 ，又 为 的中点，则 ， ， 故 . 【小问2详解】 设 的三条边 ， ， 分别为 ， ， ， 由 ，知 ， 延长 到点 ，使 ，连接 ， 则 ， ， 则在 中， ， ， 故由 与 可得， ，则 ， ，则 ， 由正弦定理得 ， 则 . 20. 已知数列 的前n项和为 ，且 . （1）证明： 是等差数列； （2）对任意正整数n，都有 ，且存在常数m，使得为定值t，求 的值. 【答案】（1）证明见解析 （2） 【解析】 【分析】（1）利用 ，将已知转化为 ，即可变形为 ， 从而证明 是等差数列.（2）根据分析数列 的性质确定 的值，再根据 是定值，化简确 定m的值，进而求出t的值，从而即可求解. 【小问1详解】 因为 ， 所以 ， 两式相减得 ，整理得 ， 所以 ，即 ， 所以 是等差数列. 【小问2详解】 由题意 ， 所以 ，解得 . 由（1）可知 是以 为首项、2为公差的等差数列，即 ， 所以 ， 而 ， 所以 ， 由题意对任意正整数n，都有 ， 所以 ，要使 定值，则 也为定值. 为 ， ， ，两式相减得： , 则 ，即 ， 则 ， 因为定值与 的大小无关，所以 ，显然 ，解得 ， 经检验，符合题意，所以 ， 所以 . 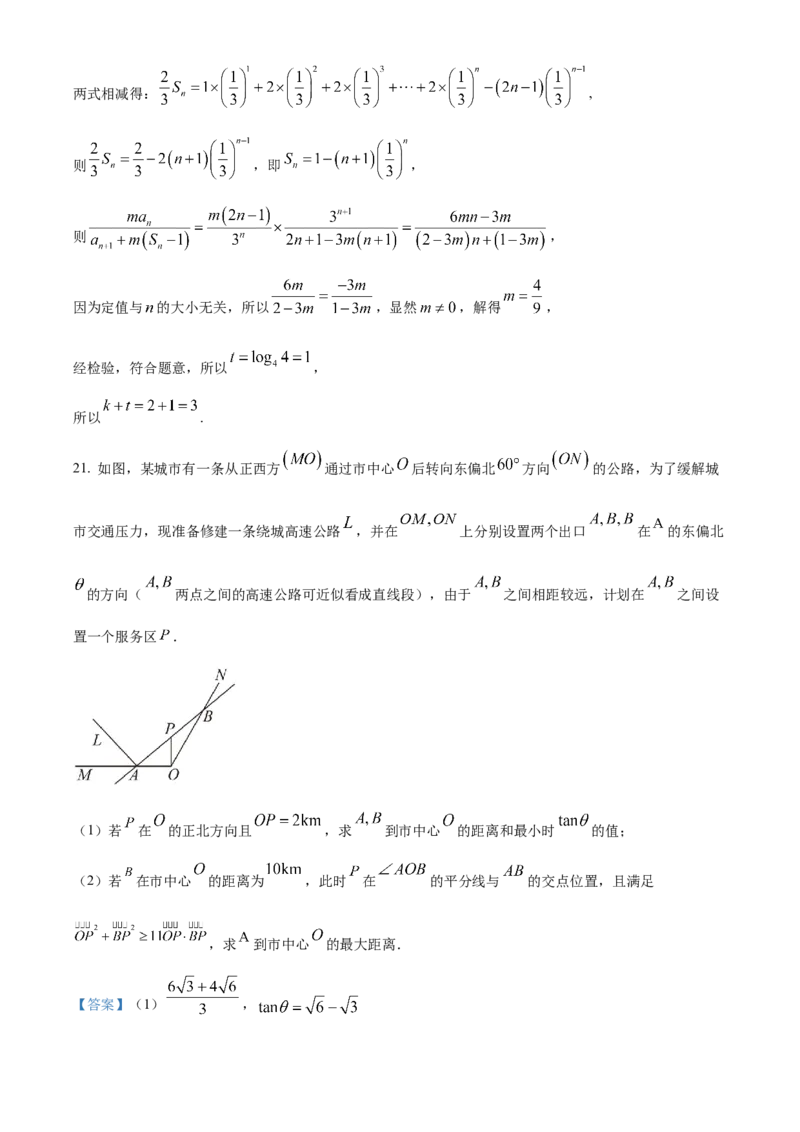21. 如图，某城市有一条从正西方 通过市中心 后转向东偏北 方向 的公路，为了缓解城 市交通压力，现准备修建一条绕城高速公路 ，并在 上分别设置两个出口 在 的东偏北 的方向（ 两点之间的高速公路可近似看成直线段），由于 之间相距较远，计划在 之间设 置一个服务区 ． （1）若 在 的正北方向且 ，求 到市中心 的距离和最小时 的值； （2）若 在市中心 的距离为 ，此时 在 的平分线与 的交点位置，且满足 ，求 到市中心 的最大距离． 【答案】（1） ，（2）20 【解析】 【分析】（1）利用正弦定理，将 分别用 表示，再利用基本不等式求 的最小值； （2）先由 化简得到 ，再根据三角形面积公式列方程得到 与的函数关系，由函数单调性求得 的最大值. 【小问1详解】 设 ，在 中， 在 中，由正弦定理得 当且仅当 ，即 时取到等号 到市中心 的距离和最小时， ． 【小问2详解】 ， ，即 ， 又 即当 时， 22. 已知函数（1）若 ，证明： 在 上恒成立； （2）若方程 有两个实数根 且 ，证明： 【答案】（1）证明见解析 （2）证明见解析 【解析】 【分析】（1）即证 ，构造 ，即可证明 ； （2）分别利用切线放缩进行证明即可. 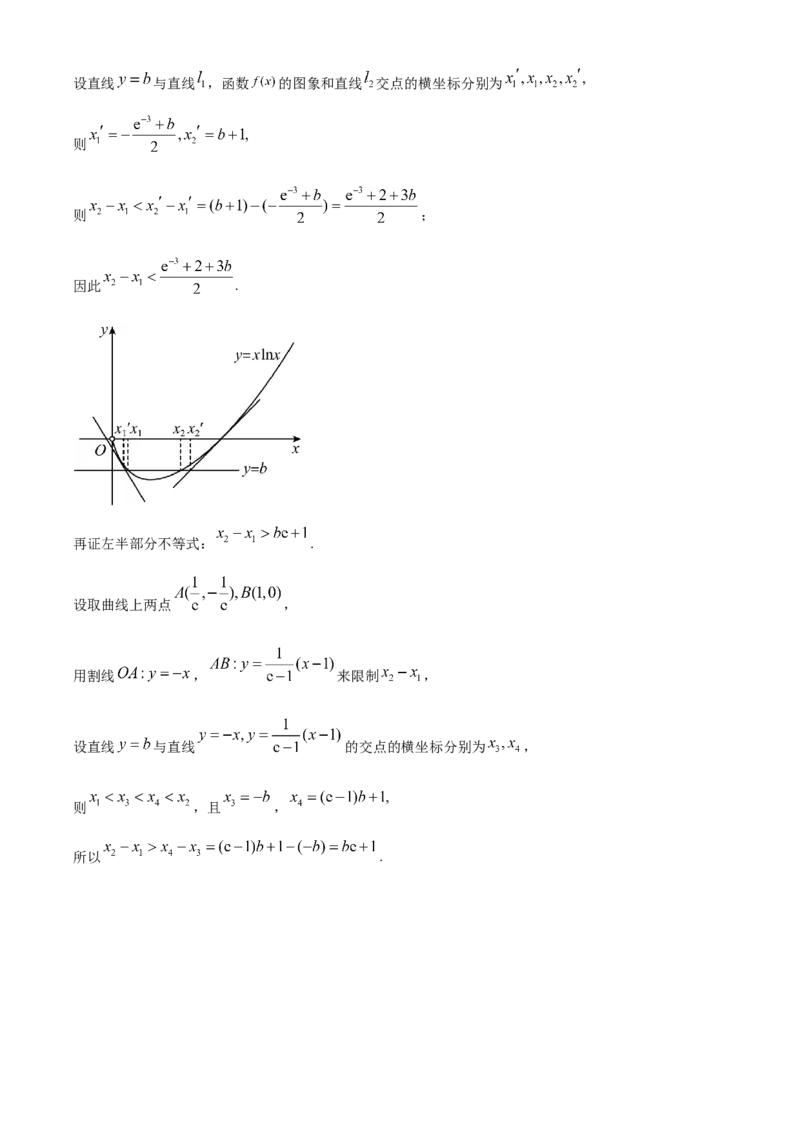【小问1详解】 因为 ， ，令 所以 ， 下证 ， 令 ， 则 ， 当 时, ，当 ， 所以 在 上单调递减，在 上单调递增， 所以 ， 所以 在 上恒成立 【小问2详解】 证明：先证右半部分不等式： ；因为 ， ， 所以 ； 的 可求曲线 在 和 处 切线分别为 和 ；设直线 与直线 ，函数 的图象和直线 交点的横坐标分别为 则 则 ； 因此 . 再证左半部分不等式： . 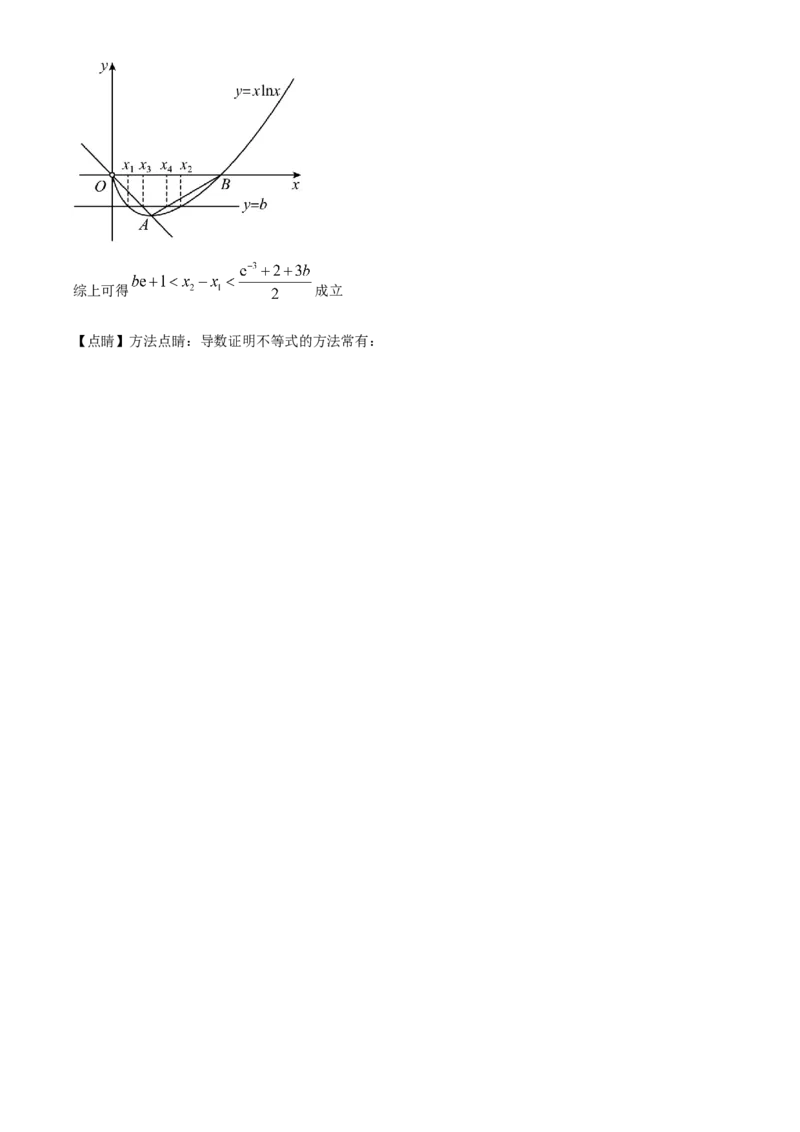设取曲线上两点 ， 用割线 ， 来限制 ， 设直线 与直线 的交点的横坐标分别为 ， 则 ，且 ， 所以 .综上可得 成立 【点睛】方法点睛：导数证明不等式的方法常有：（1）最值法：移项构造函数，通过求解最值来证明； （2）放缩法：通过构造切线或割线，利用切线放缩或者割线放缩来证明.