2005年山西高考文科数学真题及答案_数学高考真题试卷_旧1990-2007·高考数学真题_1990-2007·高考数学真题·PDF_山西

2005 年山西高考文科数学真题及答案 本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。第Ⅰ卷1至2页。第Ⅱ卷3到10 页。考试结束后，将本试卷和答题卡一并交回。 第Ⅰ卷 注意事项： 1．答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上。 2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑。如需改动，用橡皮擦 干净后，再选涂其它答案标号。不能答在试题卷上。 3．本卷共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合 题目要求的。 参考公式： 如果事件A、B互斥，那么 球是表面积公式 P(AB)  P(A)P(B) S  4R2 如果事件A、B相互独立，那么 其中R表示球的半径 P(AB)  P(A)P(B) 球的体积公式 4 如果事件A在一次试验中发生的概率是P，那么 V  R3 3 n次独立重复试验中恰好发生k次的概率 其中R表示球的半径 P (k) CkPk(1P)nk n n 一．选择题 （1）设I 为全集，S、S 、S 是I 的三个非空子集，且S S S  I ，则下面论断正 1 2 3 1 2 3 确的是 （A）C S （S S ） （B）S （C S C S） I 1 2 3 1 I 2 I 3 （C）C S C S C S ） （D）S （C S C S） I 1 I 2 I 3 1 I 2 I 3 （2）一个与球心距离为1的平面截球所得的圆面面积为，则球的表面积为 （A）8 2 （B）8 （C）4 2 （D）4 （3）函数 f(x)  x3 ax2 3x9，已知 f(x)在x  3时取得极值，则a= （A）2 （B）3 （C）4 （D）5 （4）如图，在多面体ABCDEF中，已知ABCD是边长为1的正方形，且ADE、BCF 均为 正三角形，EF∥AB，EF=2，则该多面体的体积为 2 3 （A） （B） 3 3 4 3 （C） （D） 3 2 第1页 | 共10页x2 3 （5）已知双曲线  y2 1 (a 0)的一条准线为x  ，则该双曲线的离心率为 a2 2 3 3 6 2 3 （A） （B） （C） （D） 2 2 2 3  1cos2x8sin2 x （6）当0 x  时，函数 f(x)  的最小值为 2 sin2x （A）2 （B）2 3 （C）4 （D）4 3 （7）y  2xx2 (1 x  2)反函数是 （A）y 1 1x2 (1 x 1) （B）y 1 1x2 (0 x 1) （C）y 1 1x2 (1 x 1) （D）y 1 1x2 (0 x1) （8）设0 a 1，函数 f(x) log (a2x 2ax 2)，则使 f(x)0的x的取值范围是 a （A）(,0)（B）(0,)（C）(,log 3)（D）(log 3,) a a y  x1 （9）在坐标平面上，不等式组 所表示的平面区域的面积为 y  3x 1  3 3 2 （A） 2 （B） （C） （D）2 2 2 AB （10）在ABC中，已知tan sinC，给出以下四个论断： 2 ①tanAcotB 1 ②0sin AsinB  2 ③sin2 Acos2 B 1 ④cos2 Acos2 B sin2C 其中正确的是 （A）①③ （B）②④ （C）①④ （D）②③ （11）点O是三角形ABC所在平面内的一点，满足OAOBOBOC OCOA，则点O 是ABC的 （A）三个内角的角平分线的交点 （B）三条边的垂直平分线的交点 （C）三条中线的交点 （D）三条高的交点 第2页 | 共10页（12）设直线l过点(2,0)，且与圆x2  y2 1相切，则l的斜率是 1 3 （A）1 （B） （C） （D） 3 2 3 第Ⅱ卷 注意事项： 1．用钢笔或圆珠笔直接答在试题卷上。 2．答卷前将密封线内的项目填写清楚。 3．本卷共10小题，共90分。 二．本大题共4小题，每小题4分，共16分，把答案填在题中横线上。 （13）若正整数m满足10m1  2512 10m，则m = 。(lg2 0.3010) 1 （14）(x )8的展开式中，常数项为 。（用数字作答） x （15）从6名男生和4名女生中，选出3名代表，要求至少包含1名女生，则不同的选法共 有 种。 （16）在正方形ABCD A'B'C'D'中，过对角线BD'的一个平面交AA'于E，交CC'于F， ① 四边形BFD'E一定是平行四边形 ② 四边形BFD'E有可能是正方形 ③ 四边形BFD'E在底面ABCD内的投影一定是正方形 ④ 四边形BFD'E有可能垂直于平面BB'D 以上结论正确的为 。（写出所有正确结论的编号） 三．解答题：本大题共6小题，共74分。解答应写出文字说明，证明过程或演算步骤。 （17）（本大题满分12分）  设函数 f(x) sin(2x) (0),y  f(x)图像的一条对称轴是直线x  。 8 （Ⅰ）求； （Ⅱ）求函数y  f(x)的单调增区间； （Ⅲ）画出函数y  f(x)在区间[0,]上的图像。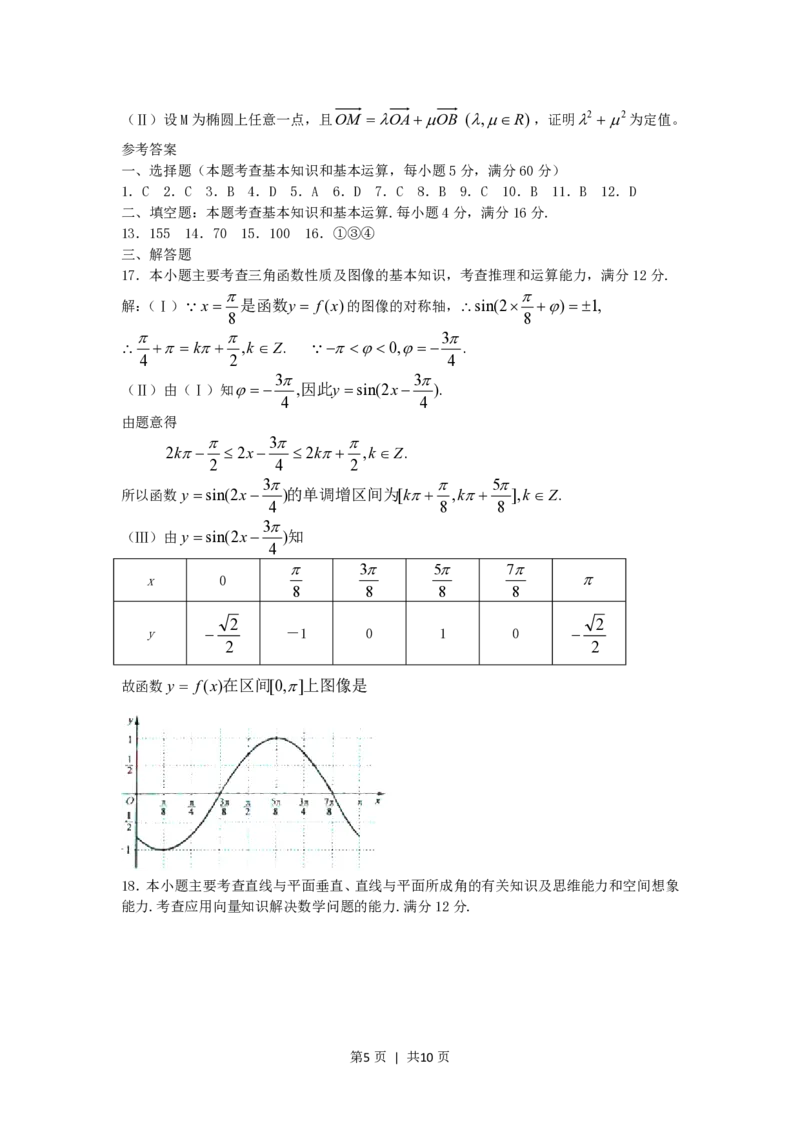 第3页 | 共10页（18）（本大题满分12分） 已知四棱锥P-ABCD的底面为直角梯形，AB∥DC，DAB 90,PA底面ABCD，且 1 PA=AD=DC= AB=1，M是PB的中点。 2 （Ⅰ）证明：面PAD⊥面PCD； （Ⅱ）求AC与PB所成的角； （Ⅲ）求面AMC与面BMC所成二面角的大小。 （19）（本大题满分12分） 已知二次函数 f(x)的二次项系数为a，且不等式 f(x)2x的解集为(1,3)。 （Ⅰ）若方程 f(x)6a 0有两个相等的根，求 f(x)的解析式； （Ⅱ）若 f(x)的最大值为正数，求a的取值范围。 （20）（本大题满分12分） 9粒种子分种在甲、乙、丙3个坑内，每坑3粒，每粒种子发芽的概率为0.5，若一个坑内 至少有1粒种子发芽，则这个坑不需要补种；若一个坑内的种子都没发芽，则这个坑需要补 种。 （Ⅰ）求甲坑不需要补种的概率； （Ⅱ）求3个坑中恰有1个坑不需要补种的概率； （Ⅲ）求有坑需要补种的概率。 （精确到0.01） （21）（本大题满分12分） 1 设正项等比数列  a  的首项a  ，前n项和为S ，且210S (210 1)S S 0。 n 1 2 n 30 20 10   （Ⅰ）求 a 的通项； n   （Ⅱ）求 nS 的前n项和T 。 n n （22）（本大题满分14分） 已知椭圆的中心为坐标原点O，焦点在x轴上，斜率为1且过椭圆右焦点F的直线交椭圆于 A、B两点，OAOB与a (3,1)共线。 （Ⅰ）求椭圆的离心率； 第4页 | 共10页（Ⅱ）设M为椭圆上任意一点，且OM OAOB (,R)，证明2 2为定值。 参考答案 一、选择题（本题考查基本知识和基本运算，每小题5分，满分60分） 1．C 2．C 3．B 4．D 5．A 6．D 7．C 8．B 9．C 10．B 11．B 12．D 二、填空题：本题考查基本知识和基本运算.每小题4分，满分16分. 13．155 14．70 15．100 16．①③④ 三、解答题 17．本小题主要考查三角函数性质及图像的基本知识，考查推理和运算能力，满分12分.   解：（Ⅰ） x  是函数y  f(x)的图像的对称轴，sin(2 )  1,  8 8   3   k ,kZ. 0,  .  4 2 4 3 3 （Ⅱ）由（Ⅰ）知  ,因此y sin(2x ). 4 4 由题意得  3  2k  2x  2k ,kZ. 2 4 2 3  5 所以函数y sin(2x )的单调增区间为[k ,k ],kZ. 4 8 8 3 （Ⅲ）由y sin(2x )知 4  3 5 7 x 0  8 8 8 8 2 2 y  －1 0 1 0  2 2 故函数y  f(x)在区间[0,]上图像是 18．本小题主要考查直线与平面垂直、直线与平面所成角的有关知识及思维能力和空间想象 能力.考查应用向量知识解决数学问题的能力.满分12分. 第5页 | 共10页方案一： （Ⅰ）证明：∵PA⊥面ABCD，CD⊥AD， ∴由三垂线定理得：CD⊥PD. 因而，CD与面PAD内两条相交直线AD，PD都垂直， ∴CD⊥面PAD. 又CD面PCD，∴面PAD⊥面PCD. （Ⅱ）解：过点B作BE//CA，且BE=CA， 则∠PBE是AC与PB所成的角. 连结AE，可知AC=CB=BE=AE= 2 ，又AB=2， 所以四边形ACBE为正方形. 由PA⊥面ABCD得∠PEB=90° BE 10 在Rt△PEB中BE= 2 ，PB= 5， cosPBE   . PB 5 10 AC与PB所成的角为arccos . 5 （Ⅲ）解：作AN⊥CM，垂足为N，连结BN. 在Rt△PAB中，AM=MB，又AC=CB， ∴△AMC≌△BMC, ∴BN⊥CM，故∠ANB为所求二面角的平面角. ∵CB⊥AC，由三垂线定理，得CB⊥PC， 在Rt△PCB中，CM=MB，所以CM=AM. AC 在等腰三角形AMC中，AN·MC= CM2 ( )2 AC ， 2 3  2 2 6 AN2 BN2  AB2 2 AN   . ∴AB=2，cosANB    5 5 2ANBN 3 2 2 故所求的二面角为arccos( ). 3 方法二：因为PA⊥PD，PA⊥AB，AD⊥AB，以A为坐标原点AD长为单位长度，如图建立空间 直角坐标系，则各点坐标为 1 A（0，0，0）B（0，2，0），C（1，1，0），D（1，0，0），P（0，0，1），M（0，1， ). 2 （Ⅰ）证明：因AP (0,0,1),DC (0,1,0),故APDC 0,所以AP  DC. 第6页 | 共10页又由题设知AD⊥DC，且AP与与AD是平面PAD内的两条相交直线，由此得DC⊥面PAD. 又DC在面PCD上，故面PAD⊥面PCD. （Ⅱ）解：因AC (1,1,0),PB (0,2,1), 故| AC | 2,| PB| 5,ACPB  2,所以 ACPB 10 cos AC,PB   . | AC || PB| 5 10 由此得AC与PB所成的角为arccos . 5 （Ⅲ）解：在MC上取一点N（x，y，z），则存在R,使NC MC, 1 1 NC (1x,1 y,z),MC (1,0, ),x 1,y 1,z  .. 2 2 1 4 要使AN  MC,只需AN MC 0即x z 0,解得 . 2 5 4 1 2 可知当 时,N点坐标为( ,1, ),能使AN MC 0. 5 5 5 1 2 1 2 此时,AN ( ,1, ),BN ( ,1, ),有BN MC 0 5 5 5 5 由AN MC 0,BN MC 0得AN  MC,BN  MC.所以ANB为所求二面角的平面 角. 30 30 4 | AN | ,| BN | ,AN BN   .  5 5 5 AN BN 2 cos(AN,BN)    . | AN || BN | 3 2 故所求的二面角为arccos( ). 3 19．本小题主要考查二次函数、方程的根与系数关系，考查运用数学知识解决问题的能力. 满分12分. 解：（Ⅰ） f(x)2x 0的解集为(1,3). f(x)2x  a(x1)(x3),且a 0.因而  f(x)  a(x1)(x3)2x  ax2 (24a)x3a.① 由方程 f(x)6a 0得ax2 (24a)x9a 0. ② 因为方程②有两个相等的根，所以 [(24a)]2 4a9a 0， 1 即 5a2 4a10. 解得a 1或a   . 5 第7页 | 共10页1 由于a 0,舍去a 1.将a   代入①得 f(x)的解析式 5 1 6 3 f(x)   x2  x . 5 5 5 12a a2 4a1 （Ⅱ）由 f(x)  ax2 2(12a)x3a  a(x )2  a a a2 4a1 及a 0,可得f(x)的最大值为 . a  a2 4a1  0, 由 a 解得 a  2 3或2 3  a 0.  a 0, 故当 f(x)的最大值为正数时，实数a的取值范围是(,2 3) (2 3,0).  20．本小题主要考查相互独立事件和互斥事件有一个发生的概率的计算方法，考查运用概率 知识解决实际问题的能力. 满分12分. 1 （Ⅰ）解：因为甲坑内的3粒种子都不发芽的概率为(10.5)3  ，所以甲坑不需要 8 补 1 7 种的概率为 1  0.875. 8 8 7 1 （Ⅱ）解：3个坑恰有一个坑不需要补种的概率为 C1 ( )2 0.041. 3 8 8 7 （Ⅲ）解法一：因为3个坑都不需要补种的概率为( )3， 8 7 所以有坑需要补种的概率为 1( )3 0.330. 8 1 7 解法二：3个坑中恰有1个坑需要补种的概率为C1 ( )2 0.287, 3 8 8 1 7 恰有2个坑需要补种的概率为 C2 ( )2  0.041, 3 8 8 1 7 3个坑都需要补种的概率为 C3( )3( )0 0.002. 3 8 8 所以有坑需要补种的概率为 0.2870.0410.0020.330. 21．本小题主要考查等比数列的基本知识，考查分析问题能力和推理能力，满分12分. 解：（Ⅰ）由 210S (210 1)S S 0 得 210(S S )  S S , 30 20 10 30 20 20 10 即210(a a  a )  a a  a , 21 22  30 11 12  20 可得210 q10(a a  a ) a a  a . 11 12  20 11 12  20 第8页 | 共10页1 1 因为a 0，所以 210q10 1, 解得q  ，因而 a  a qn1  ,n 1,2, . n 2 n 1 2n  1 1 （Ⅱ）因为{a }是首项a  、公比q  的等比数列，故 n 1 2 2 1 1 (1 ) 2 2n 1 n S  1 ,nS  n . n 1 2n n 2n 1 2 1 2 n 则数列{nS }的前n项和 T (12 n)(    ), n n  2 22  2n T 1 1 2 n1 n n  (12 n)(     ).   2 2 22 23 2n 2n1 T 1 1 1 1 n 前两式相减，得 n  (12 n)(    )   2 2 2 22 2n 2n1 1 1 (1 ) n(n1) 2 2n n n(n1) 1 n    即 T    2. 4 1 2n1 n 2 2n1 2n 1 2 22．本小题主要考查直线方程、平面向量及椭圆的几何性质等基本知识，考查综合运用数学 知识解决问题及推理的能力. 满分14分. x2 y2 （1）解：设椭圆方程为  1(ab0),F(c,0) a2 b2 x2 y2 则直线AB的方程为y  xc，代入  1，化简得 a2 b2 (a2 b2)x2 2a2cxa2c2 a2b2 0. 2a2c a2c2 a2b2 令A（x ,y ），B(x ,y ），则x x  ,x x  . 1 1 2 2 1 2 a2 b2 1 2 a2 b2 由OAOB (x  x ,y  y ),a (3,1),OAOB与a共线，得 1 2 1 2 3(y  y )(x  x ) 0,又y  x c,y  x c， 1 2 1 2 1 1 2 2 3 3(x  x 2c)(x  x ) 0, x  x  c. 1 2 1 2 1 2 2 2a2c 3c 6a 即  ，所以a2 3b2. c a2 b2  ， a2 b2 2 3 c 6 故离心率e   . a 3 x2 y2 （II）证明：（1）知a2 3b2，所以椭圆  1可化为x2 3y2 3b2. a2 b2 第9页 | 共10页设OM (x,y)，由已知得(x,y) (x ,y )(x ,y ), 1 1 2 2 x x x ,  y x 1 x 2 .  M(x,y)在椭圆上，(x 1 x 2 )2 3(y 1 y 2 )2 3b2.  1 2 即2(x2 3y2)2(x2 3y2)2(x x 3y y ) 3b2.① 1 1 2 2 1 2 1 2 3c 3 1 由（1）知x  x  ,a2  c2,b2  c2. 1 2 2 2 2 a2c2 a2b2 3 x x   c2 1 2 a2 b2 8 x x 3y y  x x 3(x c)(x c) 1 2 1 2 1 2 1 2  4x x 3(x  x )c3c2 1 2 1 2 3 9  c2  c2 3c2 2 2 0. 又x23y2 3b2,x2 3y2 3b2，代入①得2 2 1. 1 1 2 2 故2 2为定值，定值为1. 第10页 | 共10页