2005年新疆高考理科数学真题及答案_数学高考真题试卷_旧1990-2007·高考数学真题_1990-2007·高考数学真题·PDF_新疆

2005 年新疆高考理科数学真题及答案 本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分． 第I卷1至2页，第Ⅱ卷3至 10页。考试结束后，将本试卷和答题卡一并交回． 第I卷 注意事项： 1．答第I卷前，考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上。 2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑。如需改动，用橡皮擦 干净后，再选涂其它答案标号。不能答在试题卷上。 3．本卷共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合 题目要求的。 参考公式： 如果事件A、B互斥，那么 球的表面积公式 P(A+B)=P(A)+P(B) S 4R2 如果事件A、B相互独立，那么 其中R表示球的半径 P(A·B)=P(A)·P(B) 如果事件A在一次试验中发生的概率是 球的体积公式 4 P，那么n次独立重复试验中恰好发生k V  R3 3 次的概率P (k) CkPk(1P)nk 其中R表示球的半径 n n 一、选择题： Y C 1．函数f(x)=|sinx+cosx|的最小正周期是 （ ） Y   A． B． C．π D．2π 4 2 2．正方体ABCD—ABCD 中，P、Q、R分别是AB、AD、BC 的中点。那么，正方体的 1 1 1 1 1 1 过P、Q、R的截面图形是 （ ） A．三角形 B．四边形 C．五边形 D．六边形 3．函数y  3 x2 1(x 0)的反函数是 （ ） A．y  (x1)3(x  1) B．y   (x1)3(x  1) C．y  (x1)3(x 0) D．y   (x1)3(x 0) 第1页 | 共8页  4．已知函数y  tanx在( , )内是减函数，则 （ ） 2 2 A．0<≤1 B．－1≤<0 C．≥1 D．≤－1 abi 5．设a、b、c、d∈R，若 为实数，则 （ ） cdi A．bc+ad≠0 B．bc－ad≠0 C．bc－ad=0 D．bc+ad=0 x2 y2 6．已知双曲线  1的焦点为F、F，点M在双曲线上且MF⊥x轴，则F 到直线FM 1 2 1 1 2 6 3 的距离为 （ ） 3 6 5 6 6 5 A． B． C． D． 5 6 5 6 1 7．锐角三角形的内角A、B满足tanA－ =tanB，则有 （ ） sin2A A．sin2A－cosB=0 B．sin2A+cosB=0 C．sin2A－sinB=0 D．sin2A+sinB=0 8．已知点A（ 3，1），B（0，0）C（ 3，0）.设∠BAC的平分线AE与BC相交于E， 那么有BC CE,其中等于 （ ） 1 1 A．2 B． C．－3 D．－ 2 3 9．已知集合M={x|x2－3x－28≤0}, N={x|x2－x－6>0}，则M∩N为 （ ） A．{x|－4≤x<－2或33} D．{x|x<－2或x≥3} 10．点P在平面上作匀速直线运动，速度向量v=（4，－3）（即点P的运动方向与v相同， 且每秒移动的距离为|v|个单位.设开始时点P的坐标为（－10，10），则5秒后点P的 坐标为 （ ） A．（－2，4） B．（－30，25） C．（10，－5） D．（5，－10） 11．如果a, a, …,a 为各项都大于零的等差数列，公差d≠0，则 （ ） 1 2 8 A．aa>aa B．aaa+a D．aa=aa 1 8 4 5 1 8 4 5 1 8 4 5 1 8 4 5 12．将半径都为1的4个铅球完全装人形状为正四面体的容品里，这个正四面体的高最小值 为 （ ） 32 6 2 6 2 6 4 32 6 A． B．2 C．4 D． 3 3 3 3 第2页 | 共8页第Ⅱ卷 注意事项： 1．用钢笔或圆珠笔直接答在试题卷中。 2．答卷前将密封线内的项目填写清楚。 3．本卷共10小题，共90分。 二、填空题：本大题共4小题，每小题4分，共16分.把答案填在题中横线上. Y C 13．圆心为（1，2）且与直线5x－12y－7=0相切的圆的方程为 . Y sin3 13 14．设为第四象限的角，若  ,则tan2= . sin 5 15．在由数字0，1，2，3，4，5所组成的没有重复数字的四位数中，不能被5整除的数共 有 个. 16．下面是关于三棱锥的四个命题： ①底面是等边三角形，侧面与底面所成的二面角都相等的三棱锥是正三棱锥. ②底面是等边三角形，侧面都是等腰三角形的三棱锥是正三棱锥. ③底面是等边三角形，侧面的面积都相等的三棱锥是正三棱锥. ④侧棱与底面所成的角都相等，且侧面与底面所成的二面角都相等的三棱锥是正三棱锥.其 中，真命题的编号是 （写出所有真命题的编号）. 三、解答题：（本大题共6小题，共74分.解答应写出文字说明，证明过程或演算步骤.） 17．（本小题满分12分） 设函数 f(x)  2|x1||x1|,求使f(x) 2 2x的取值范围. 18．（本小题满分12分） 已知{a }是各项均为正数的等差数列，lga 、lga 、lga 成等差数列.又 n 1 2 4 1 b  ,n 1,2,3, . n a  2n （Ⅰ）证明{b }为等比数列； n 1 （Ⅱ）如果无穷等比数列{b }各项的和S  ，求数列{a }的首项a和公差d. 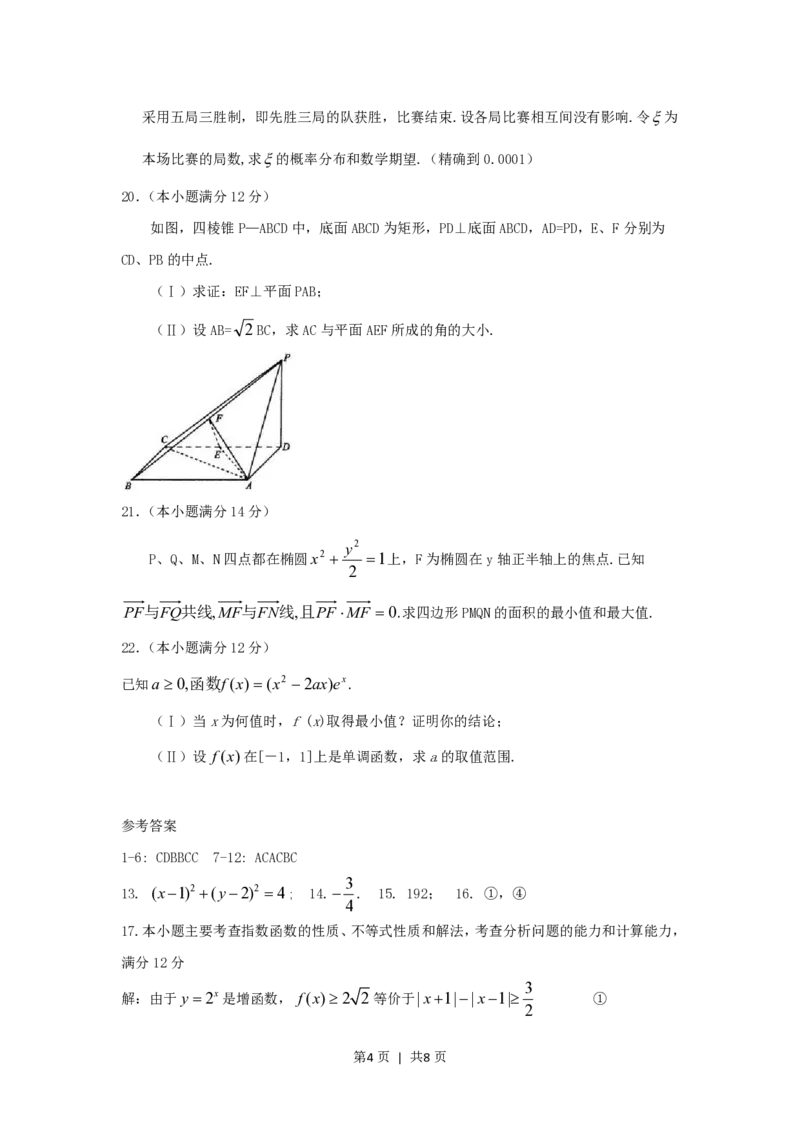n 3 n 1 （注：无穷数列各项的和即当n 时数列前n项和的极限） 19．（本小题满分12分） 甲、乙两队进行一场排球比赛.根据以往经验，单局比赛甲队胜乙队的概率为0.6.本场比赛 第3页 | 共8页采用五局三胜制，即先胜三局的队获胜，比赛结束.设各局比赛相互间没有影响.令为 本场比赛的局数,求的概率分布和数学期望.（精确到0.0001） 20．（本小题满分12分） 如图，四棱锥P—ABCD中，底面ABCD为矩形，PD⊥底面ABCD，AD=PD，E、F分别为 CD、PB的中点. （Ⅰ）求证：EF⊥平面PAB； （Ⅱ）设AB= 2 BC，求AC与平面AEF所成的角的大小. 21．（本小题满分14分） y2 P、Q、M、N四点都在椭圆x2  1上，F为椭圆在y轴正半轴上的焦点.已知 2 PF与FQ共线,MF与FN线,且PFMF 0.求四边形PMQN的面积的最小值和最大值. 22．（本小题满分12分） 已知a 0,函数f(x) (x2 2ax)ex. （Ⅰ）当x为何值时，f (x)取得最小值？证明你的结论； （Ⅱ）设 f(x)在[－1，1]上是单调函数，求a的取值范围. 参考答案 1-6: CDBBCC 7-12: ACACBC 3 13. (x1)2 (y2)2 4; 14. . 15. 192； 16. ①，④ 4 17.本小题主要考查指数函数的性质、不等式性质和解法，考查分析问题的能力和计算能力， 满分12分 3 解：由于y 2x是增函数， f(x)2 2 等价于|x1||x1| ① 2 第4页 | 共8页（1） 当x1时，|x1||x1|2，①式恒成立。 3 3 （2） 当1 x1时，|x1||x1|2x，①式化为2x ，即  x1 2 4 （3） 当x1时，|x1||x1|2，①式无解 3  综上x的取值范围是  ,  4  18.本小题主要考查等差数列、等比数列的基本知识以及运用这些知识的能力。满分12分。 （Ⅰ）证明： lga 、lga 、lga 成等差数列，2lga lga lga ，即a 2 aa  1 2 4 2 1 4 2 1 4 又设等差数列a 的公差为d ，则(a d)2 a (a 3d)，即d2 ad n 1 1 1 1 1 1 1 d 0,d a 0，a a (2n 1)d 2nd，b     1 2n 1 n a d 2n 2n 1 1 这时b 是首项b  ，公比为 的等比数列。 n 1 2d 2 （Ⅱ）解：如果无穷等比数列b 的公比q 1，则当n时其前n项和的极限不存在。 n 1 1 [1( )n] 因而d a 0，这时公比q 1 ，b  1 ，这样b 的前n项和S  2d 2 . 1 2 1 2d n n 1 1 2 1 1 [1( )n] 2d 2 1 则S limS lim  . n n n 1 d 1 2 1 由S  得公差d 3，首项a d 3. 3 1 19.本小题考查离散型随机变量分布和数学期望等概念，考查运用概率知识解决实际问题的 能力。满分12分 解：单局比赛甲队胜乙队的概率为0.6，乙队胜甲队的概率为1－0.6＝0.4 比赛3局结束有两种情况：甲队胜3局或乙队胜3局，因而P（＝3）＝0.630.43 0.28 比赛4局结束有两种情况：前3局中甲队胜2局，第4局甲队胜；或前3局中乙队胜2局， 第4局乙队胜。因而 P（＝4）＝C20.620.40.6＋C20.420.60.40.3744 3 3 比赛5局结束有两种情况：前4局中甲队胜2局、乙队胜2局，第5局甲胜或乙胜。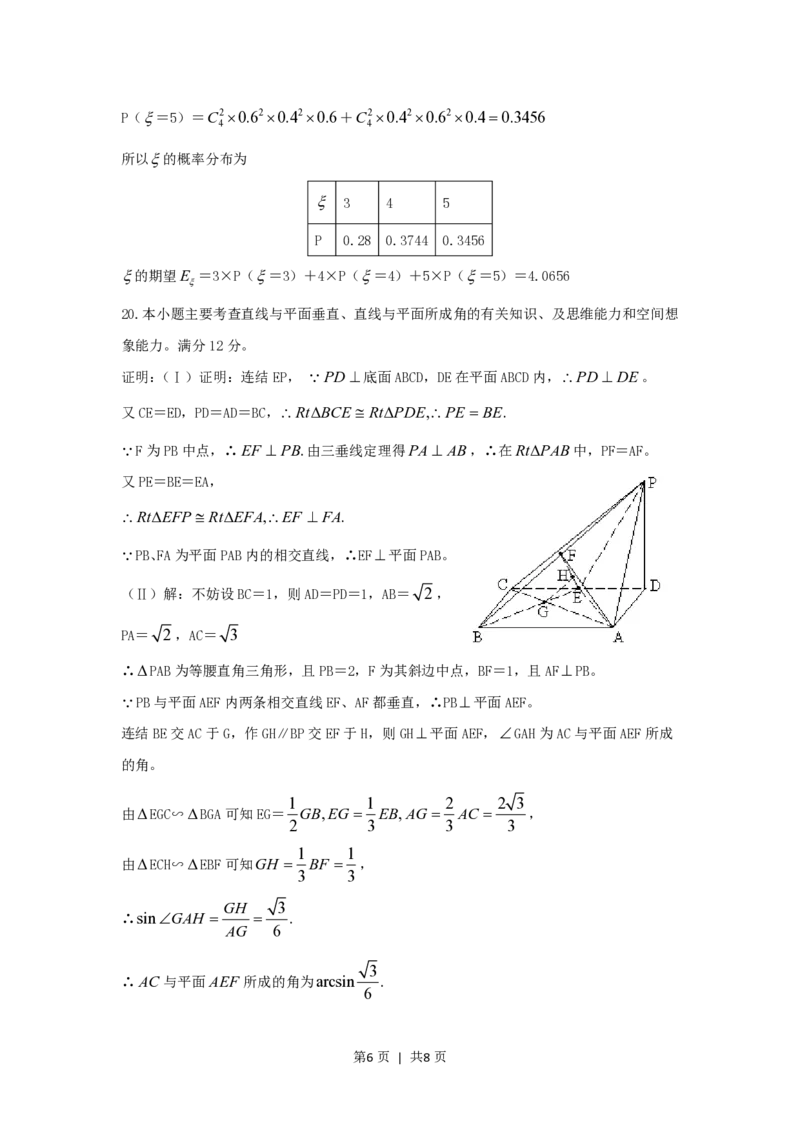因而 第5页 | 共8页P（＝5）＝C20.620.420.6＋C20.420.620.40.3456 4 4 所以的概率分布为  3 4 5 P 0.28 0.3744 0.3456 的期望E ＝3×P（＝3）＋4×P（＝4）＋5×P（＝5）＝4.0656  20.本小题主要考查直线与平面垂直、直线与平面所成角的有关知识、及思维能力和空间想 象能力。满分12分。 证明：（Ⅰ）证明：连结EP， PD底面ABCD，DE在平面ABCD内，PD DE。  又CE＝ED，PD＝AD＝BC，RtBCE  RtPDE,PE  BE. F为PB中点，∴EF  PB.由三垂线定理得PA AB，∴在RtPAB中，PF＝AF。  又PE＝BE＝EA， RtEFP RtEFA,EF  FA. PB、FA为平面PAB内的相交直线，∴EF平面PAB。  （Ⅱ）解：不妨设BC＝1，则AD＝PD＝1，AB＝ 2 ， PA＝ 2 ，AC＝ 3 ∴PAB为等腰直角三角形，且PB＝2，F为其斜边中点，BF＝1，且AFPB。 PB与平面AEF内两条相交直线EF、AF都垂直，∴PB平面AEF。  连结BE交AC于G，作GH∥BP交EF于H，则GH平面AEF，GAH为AC与平面AEF所成 的角。 1 1 2 2 3 由EGC∽BGA可知EG＝ GB,EG  EB,AG  AC  ， 2 3 3 3 1 1 由ECH∽EBF可知GH  BF  ， 3 3 GH 3 ∴sinGAH   . AG 6 3 ∴AC与平面AEF 所成的角为arcsin . 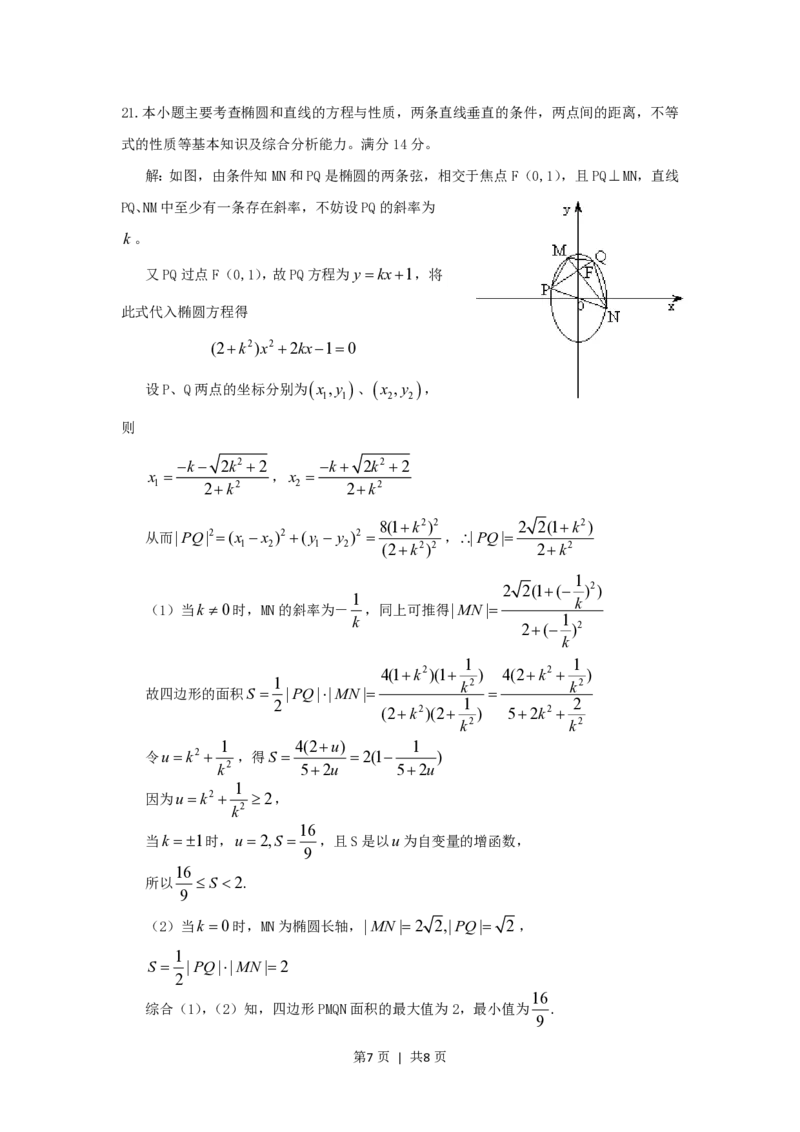6 第6页 | 共8页21.本小题主要考查椭圆和直线的方程与性质，两条直线垂直的条件，两点间的距离，不等 式的性质等基本知识及综合分析能力。满分14分。 解：如图，由条件知MN和PQ是椭圆的两条弦，相交于焦点F（0,1），且PQMN，直线 PQ、NM中至少有一条存在斜率，不妨设PQ的斜率为 k。 又PQ过点F（0,1），故PQ方程为y kx1，将 此式代入椭圆方程得 (2k2)x2 2kx10 设P、Q两点的坐标分别为x ,y 、x ,y ， 1 1 2 2 则 k 2k2 2 k 2k2 2 x  ，x  1 2k2 2 2k2 8(1k2)2 2 2(1k2) 从而|PQ|2(x x )2 (y  y )2  ，|PQ| 1 2 1 2 (2k2)2 2k2 1 2 2(1( )2) 1 k （1）当k 0时，MN的斜率为－ ，同上可推得|MN | k 1 2( )2 k 1 1 4(1k2)(1 ) 4(2k2  ) 1 k2 k2 故四边形的面积S  |PQ||MN |  2 1 2 (2k2)(2 ) 52k2  k2 k2 1 4(2u) 1 令u k2  ，得S  2(1 ) k2 52u 52u 1 因为u k2  2， k2 16 当k 1时，u 2,S  ，且S是以u为自变量的增函数， 9 16 所以 S 2. 9 （2）当k 0时，MN为椭圆长轴，|MN |2 2,|PQ| 2 ， 1 S  |PQ||MN |2 2 16 综合（1），（2）知，四边形PMQN面积的最大值为2，最小值为 . 9 第7页 | 共8页22．本小题主要考查导数的概念和计算，应用导数研究函数性质的方法及推理和运算能力。 满分12分。 解：（I）对函数 f(x)求导数，得 f(x)(x22ax)ex (2x2a)ex [x22(1a)x2a]ex. 已知a 0，函数 f(x) (x2 2ax)ex． （Ⅰ）当x为何值时，f(x)取得最小值？证明你的结论； （Ⅱ）设f(x)在[-1,1]上是单调函数，求a的取值范围． 令 f (x) 0，得[x22(1a)x2a]ex 0，从而x22(1a)x2a0， 解得x a1 1a2 ，x a1 1a2 ，其中x  x 1 2 1 2 当x变化时， f (x), f(x)的变化情况如下表： x ,x  x (x ,x ) x x , 1 1 1 2 2 2 f (x) ＋ 0 － 0 ＋ f(x) 极大值 极小值 当 f(x)在x x 处取到极大值，在x x 处取到极小值。 1 2 当a0时，x 1，x 0， f(x)在(x ,x )上为减函数，在x ,上为增函数， 1 2 1 2 2 而当x0时， f(x) x(x2a)ex 0；当x0时， f(x)0. 所以当xa1 1a2 时， f(x)取得最小值。 （II）当a0时， f(x)在[1,1]上为单调函数的充要条件是x 1， 2 3 即a1 1a2 1，解得a 。 4 3 综上， f(x)在[1,1]上为单调函数的充要条件a 。 4 3  即a的取值范围是  , 。 4  第8页 | 共8页