文档内容
清新区 2024-2025 学年高三上学期 12 月期末四校联考
数学试题
满分150分,考试用时120分钟.
注意事项:
1.答题前,先将自己的姓名、准考证号、考场号、座位号填写在试卷和答题卡上,并将准考
证号条形码粘贴在答题卡上的指定位置.
2.非选择题的作答:用黑色签字笔直接答在答题卡上对应的答题区域内.写在试卷、草稿纸
和答题卡上的非答题区域均无效.
一、单选题(本题共 8 小题,每小题 5 分,共 40 分.)
1. 已知集合 , ,则 ( )
A. B. C. D.
【答案】D
【解析】
【分析】先求得集合 ,再根据交集定义得解.
【详解】∵ ,
,
∴ ,
故选:D.
2. 复数 等于它共轭复数的倒数的充要条件是( )
A. B. C. D.
【答案】B
【解析】
【详解】令 则 .由 得 ,
第1页/共27页
学科网(北京)股份有限公司故选B.
3. 在等比数列 中, ,则 ( )
A. 4 B. C. 8 D. 5
【答案】A
【解析】
【分析】由等比数列基本量的计算首先得公比,进一步得首项,由此即可得解.
【详解】由题意 ,所以 ,即等比数列公比为 ,
所以 ,解得 ,所以 .
故选:A.
4. 抛物线 的准线方程为( )
A. B. C. D.
【答案】B
【解析】
【分析】把抛物线方程化为标准形式,结合准线方程的特点进行求解即可.
【详解】抛物线C的标准方程为 ,所以其准线方程为 ,
故选:B
5. 已知F,F 分别是双曲线C: 的左、右焦点,点P在双曲线上, ,
1 2
圆O: ,直线PF 与圆O相交于A,B两点,直线PF 与圆O相交于M,N两点.若四
1 2
边形AMBN的面积为 ,则C的离心率为( )
A. B. C. D.
第2页/共27页
学科网(北京)股份有限公司【答案】D
【解析】
【分析】设 , ,有 , , ,由弦长公式可得
, ,四边形AMBN的面积为 ,解得
,可求双曲线的离心率.
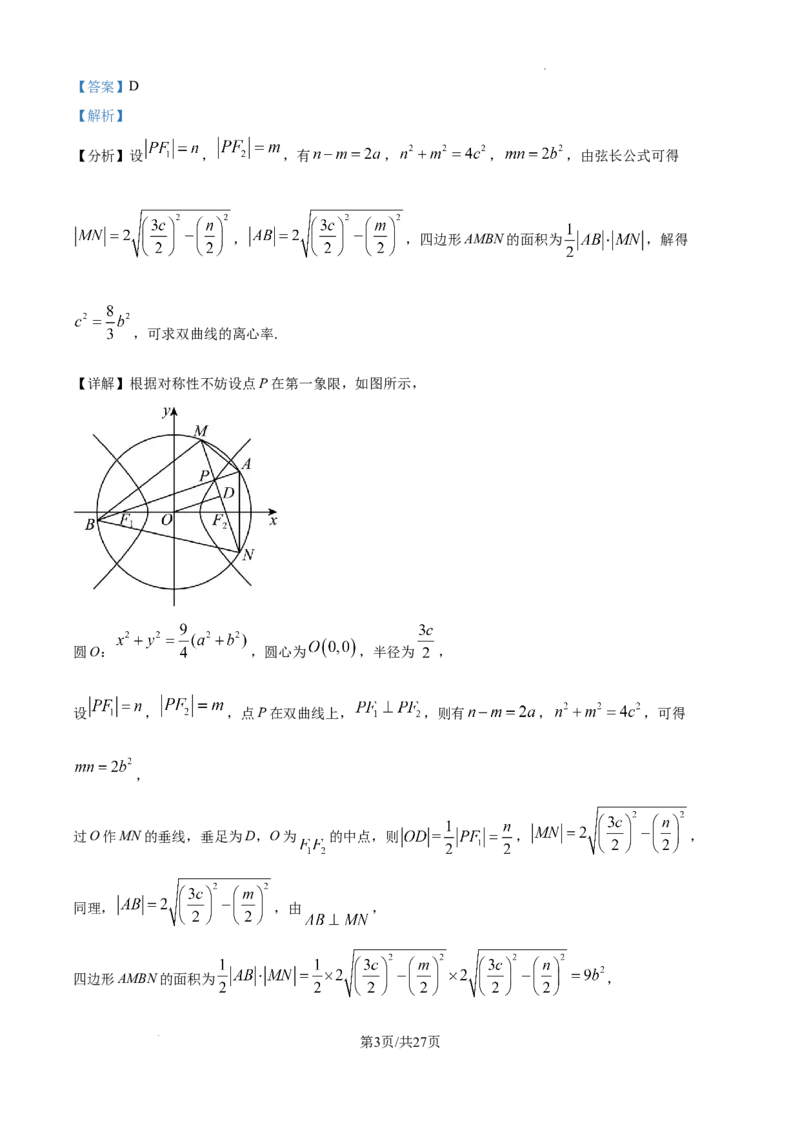
【详解】根据对称性不妨设点P在第一象限,如图所示,
圆O: ,圆心为 ,半径为 ,
设 , ,点P在双曲线上, ,则有 , ,可得
,
过O作MN的垂线,垂足为D,O为 的中点,则 , ,
同理, ,由 ,
四边形AMBN的面积为 ,
第3页/共27页
学科网(北京)股份有限公司,化简得 ,则有
,则C的离心率 .
故选:D
6. 过圆 上一点 作圆 的两条切线,切点分别为 , ,若 ,
则实数 ( )
A. B. C. D.
【答案】C
【解析】
【分析】取圆 上任意一点P,过P作圆 的两条切线 , ,根据题
中条件,求出 ,进而可求出结果.
【详解】取圆 上任意一点P,
过P作圆 的两条切线 , ,
当 时, 且 , ;
则 ,所以实数 .
第4页/共27页
学科网(北京)股份有限公司.
故选:C
【点睛】本题主要考查求由直线与圆相切求参数,属于基础题型.
7. 甲、 乙、丙等5名同学参加政史地三科知识竞赛,每人随机选择一科参加竞赛,则甲和乙不参加同一科
甲和丙参加同一科竞赛,且这三科竞赛都有人参加的概率为( )
A. B. C. D.
【答案】C
【解析】
【分析】由排列组合知识结合概率公式即可得解.
【详解】因为甲和乙不参加同一科,甲和丙参加同一科竞赛,若每个同学可以自由选择,
所以3科的选择数有2,2,1和3,1,1两种分配方案,
当分配方案为2,2,1时,共有 种不同的选择方案;
当分配方案为3,1,1时,共有 种不同的选择方案;
所以满足要求的不同选择种数为 ;
所以甲和乙不参加同一科,甲和丙参加同一科竞赛,且这三科竞赛都有人参加的概率为 .
故选:C.
8. 已知函数 在区间 上有且只有一个最大值和一个最小值,则 的取值范
围是( )
A. B.
C. D.
【答案】D
【解析】
【分析】根据正弦型函数的最值性质进行求解即可.
第5页/共27页
学科网(北京)股份有限公司【详解】因为 得,则 ,
所以由题意可得, ,解得 .
故选:D
二、多选题(本题共 4 小题,每小题 6 分,共 24 分.每题至少两项是符合题目要求的.
全部选对得 6 分,部分选对的得部分分,选对但不全的得部分分,有选错的得0分.)
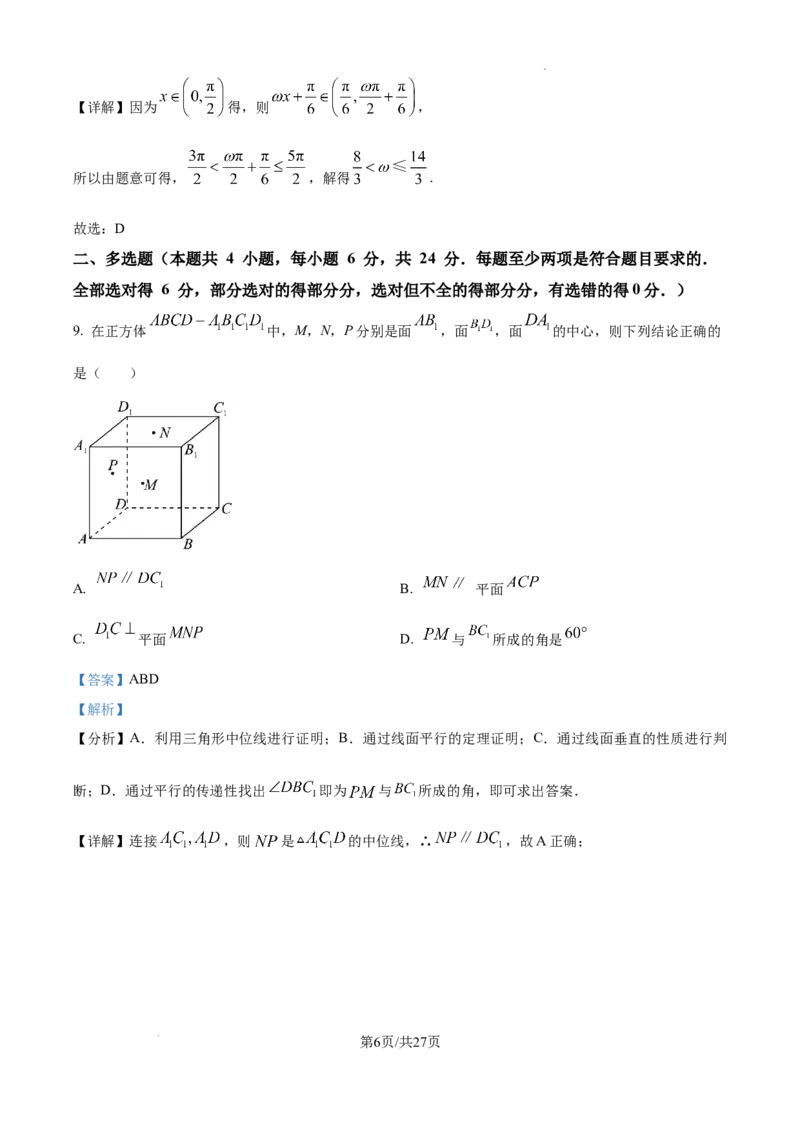
9. 在正方体 中,M,N,P分别是面 ,面 ,面 的中心,则下列结论正确的
是( )
A. B. 平面
C. 平面 D. 与 所成的角是
【答案】ABD
【解析】
【分析】A.利用三角形中位线进行证明;B.通过线面平行的定理证明;C.通过线面垂直的性质进行判
断;D.通过平行的传递性找出 即为 与 所成的角,即可求出答案.
【详解】连接 ,则 是 的中位线,∴ ,故A正确;
第6页/共27页
学科网(北京)股份有限公司连接 , ,则 , 平面 , 平面 ,
∴ 平面 ,即 平面 ,故B正确;
连接 ,则平面 即为平面 ,显然 不垂直平面 ,故C错误;
∵ ,∴ 或其补角为 与 所成的角, ,故D正确.
故选:ABD.
10. 下列结论正确的是( )
A. 若 ,则
B. 若 ,则 的最小值为2
C. 若 ,则 的最大值为2
D. 若 ,则
【答案】AD
【解析】
【分析】利用作差法比较大小判断A,利用基本(均值)不等式判断BCD,要注意“一正二定三相等”.
【详解】因为 ,所以 ,
因为 ,所以 ,所以 ,故A正确;
因为 的等号成立条件 不成立,所以B错误;
第7页/共27页
学科网(北京)股份有限公司因为 ,所以 ,故C错误;
因为 ,
当且仅当 ,即 时,等号成立,所以D正确.
故选:AD
11. 已知圆 ,圆 分别是圆 与圆 上的点,则(
)
A. 若圆 与圆 无公共点,则
B. 当 时,两圆公共弦所在直线方程为
C. 当 时,则 斜率的最大值为
D. 当 时,过 点作圆 两条切线,切点分别为 ,则 不可能等于
【答案】BC
【解析】
【分析】对于A,当两圆内含时即可判断错误;对于B,两圆方程相减即可验算;对于C,画出公切线通
过数形结合即可验算;对于D,画出圆 两条切线,通过数形结合即可验算.
【详解】对于选项A,当两圆内含时, 可以无穷大,所以A不正确;
当 时两圆相交,两圆的方程作差可以得公共弦的直线方程为 ,所以B为正确选项;
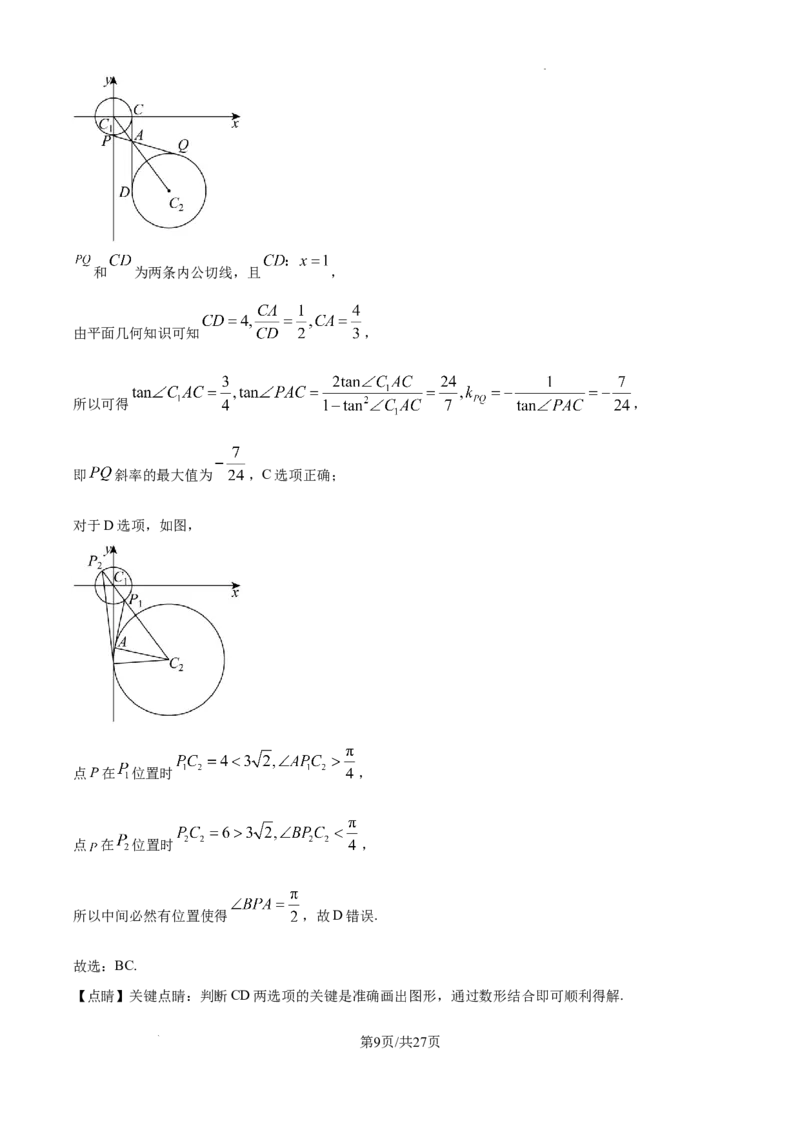
对于选项B,当 时如图,
第8页/共27页
学科网(北京)股份有限公司和 为两条内公切线,且 ,
由平面几何知识可知 ,
所以可得 ,
即 斜率的最大值为 ,C选项正确;
对于D选项,如图,
点P在 位置时 ,
点 在 位置时 ,
所以中间必然有位置使得 ,故D错误.
故选:BC.
【点睛】关键点睛:判断CD两选项的关键是准确画出图形,通过数形结合即可顺利得解.
第9页/共27页
学科网(北京)股份有限公司12. 已知函数 , ,其中 且 .若函数 ,
则下列结论正确的是( )
A. 当 时, 有且只有一个零点
B. 当 时, 有两个零点
C. 当 时,曲线 与曲线 有且只有两条公切线
D. 若 为单调函数,则
【答案】BCD
【解析】
【分析】A. 通过举特例说明该选项错误;B. 考虑 ,
求出函数的单调性,分析图象得到 有两个零点;C.求出两曲线的切线方程,再建立方程组,转化为
零点个数问题分析得解;D. 分 单调递增和单调递减讨论,从而求出 得解.
【详解】对A, 令 ,
令 或 都成立, 有两个零点,故A错误;
对B, 令
,( ).考虑
所以函数 在 单调递减,在 单调递增,
.
第10页/共27页
学科网(北京)股份有限公司考虑
所以函数 在 单调递增,在 单调递减, 当 时,
,所以当 时,有两个零点.
此时 ,故B正确;
对C,设 , .
设切点
所以 .
①
②
,
,
设 ,
所以 ,
所以函数 在 单调递减,因为 ,
第11页/共27页
学科网(北京)股份有限公司所以
所以 有两解,所以当 时,曲线 与曲线 有且只有两条公切线,所以该选
项正确;
对D,若 单调递增,则 .
.考虑 不满足.
若 单调递减,则 .
所以 考虑 不满足.
当 时, 不满足.
当 时,
,∴ .故D正确.
故选:BCD
【点睛】关键点睛:本题主要有四个关键,其一,是逻辑思维,证明命题是错误的,只要举出反例即可;
其二,要熟练掌握利用导数讨论函数的零点个数;其三,是理解掌握曲线公切线的研究方法;其四,要会
根据函数的单调性求参数的范围.
三、填空题(本题共4小题,每小题4分,共16分)
13. 第二届广东自由贸易试验区一联动发展区合作交流活动于2023年12月13日—14日在湛江举行,某区
共有4名代表参加,每名代表是否被抽到发言相互独立,且概率均为 ,记 为该区代表中被抽到发言的
人数,则 ______.
第12页/共27页
学科网(北京)股份有限公司【答案】 ##
【解析】
【分析】根据题意可知随机变量为 ,利用方差公式 从而可求解.
【详解】由题意知随机变量为 ,
所以 ,
故答案 :为.
14. 函数 是奇函数,则 __________.
【答案】1
【解析】
【分析】根据奇函数的性质,结合对数运算,即可求解 ,再代入函数解析式求值.
【详解】因为 ,所以 ,
因为 是奇函数,所以 ,即 ,
所以 ,解得 ,
则 .
故答案为:1
15. 已知向量 , ,则使 成立的一个充分不必要条件是
______________.
【答案】 (答案不唯一)
【解析】
第13页/共27页
学科网(北京)股份有限公司【分析】根据向量坐标运算公式将原问题转化为 的一个充分不必要条件进而求解.
【详解】因为 , ,
所以 , ,
所以 ,
解得 ,
所以使 成立的一个充分不必要条件是 .
故答案为: (答案不唯一)
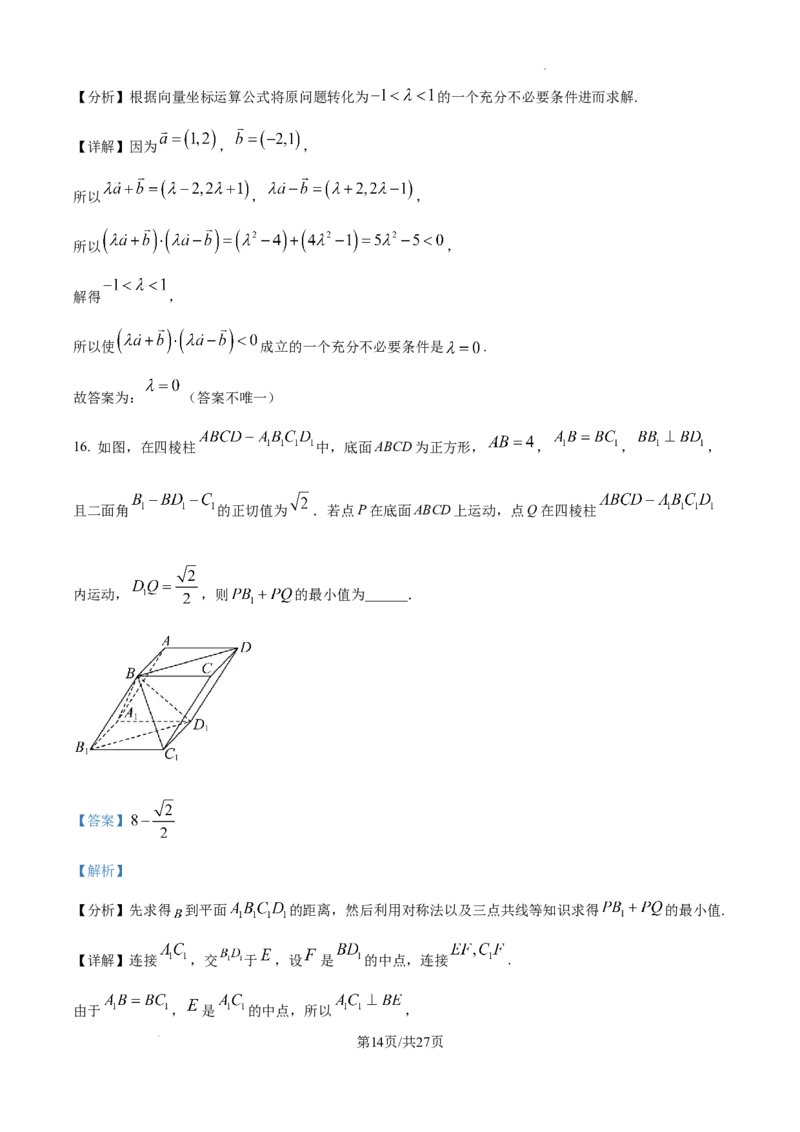
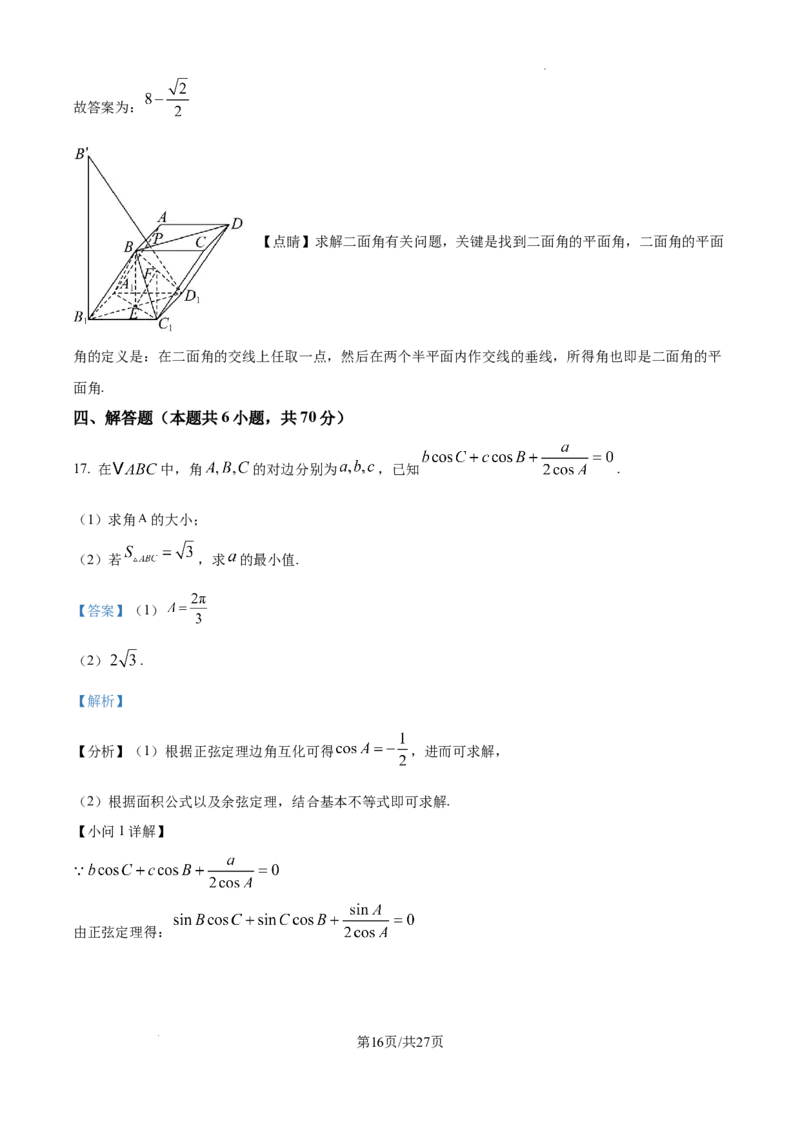
16. 如图,在四棱柱 中,底面ABCD为正方形, , , ,
且二面角 的正切值为 .若点P在底面ABCD上运动,点Q在四棱柱
内运动, ,则 的最小值为______.
【答案】
【解析】
【分析】先求得 到平面 的距离,然后利用对称法以及三点共线等知识求得 的最小值.
【详解】连接 ,交 于 ,设 是 的中点,连接 .
由于 , 是 的中点,所以 ,
第14页/共27页
学科网(北京)股份有限公司由于 平面 ,
所以 平面 ,由于 平面 ,所以 , ,
由于 分别是 的中点,所以 ,
由于 ,所以 ,由于 平面 ,
所以 平面 ,由于 平面 ,所以 ,
所以 是二面角 的平面角,
所以 ,所以 ,
由于 ,所以 ,
所以三角形 是等腰直角三角形,所以 ,
由于 平面 ,
所以 平面 ,且 .
由于 ,所以 点的轨迹是以 为球心,
半径为 的球面在四棱柱 内的部分,
关于平面 的对称点为 ,
连接 ,交平面 于 ,
所以 的最小值为 .
第15页/共27页
学科网(北京)股份有限公司故答案为:
【点睛】求解二面角有关问题,关键是找到二面角的平面角,二面角的平面
角的定义是:在二面角的交线上任取一点,然后在两个半平面内作交线的垂线,所得角也即是二面角的平
面角.
四、解答题(本题共6小题,共70分)
17. 在 中,角 的对边分别为 ,已知 .
(1)求角 的大小;
(2)若 ,求 的最小值.
【答案】(1)
(2) .
【解析】
【分析】(1)根据正弦定理边角互化可得 ,进而可求解,
(2)根据面积公式以及余弦定理,结合基本不等式即可求解.
【小问1详解】
由正弦定理得:
第16页/共27页
学科网(北京)股份有限公司,
又 , ,
,
;
【小问2详解】
, ,
由余弦定理得: ,
当且仅当 时等号成立,
,即 的最小值为 .
18. 设 是等比数列且公比 大于0,其前 项和为 是等差数列,已知 ,
.
(1)求 的通项公式;
(2)设 ,数列 的前 项和为 ,求满足 的最大整数 的值.
【答案】(1) , ;
(2)9.
【解析】
【分析】(1)利用等差和等比数列的通项公式求解;
(2)先拆项分母得 ,再利用裂项相消法求和,进而解不等式求满足 的最
第17页/共27页
学科网(北京)股份有限公司大整数 的值.
【小问1详解】
设 的公比为 ,
因为 ,所以 ,即 ,解得 或 (舍),
所以 ,
设 的公差为 ,
为
因 ,所以 ,
所以 ,解得 ,所以 .
故 , .
【小问2详解】
,
即 .
所以
.
,化简得 ,又 ,解得 .
所以满足 的最大整数 .
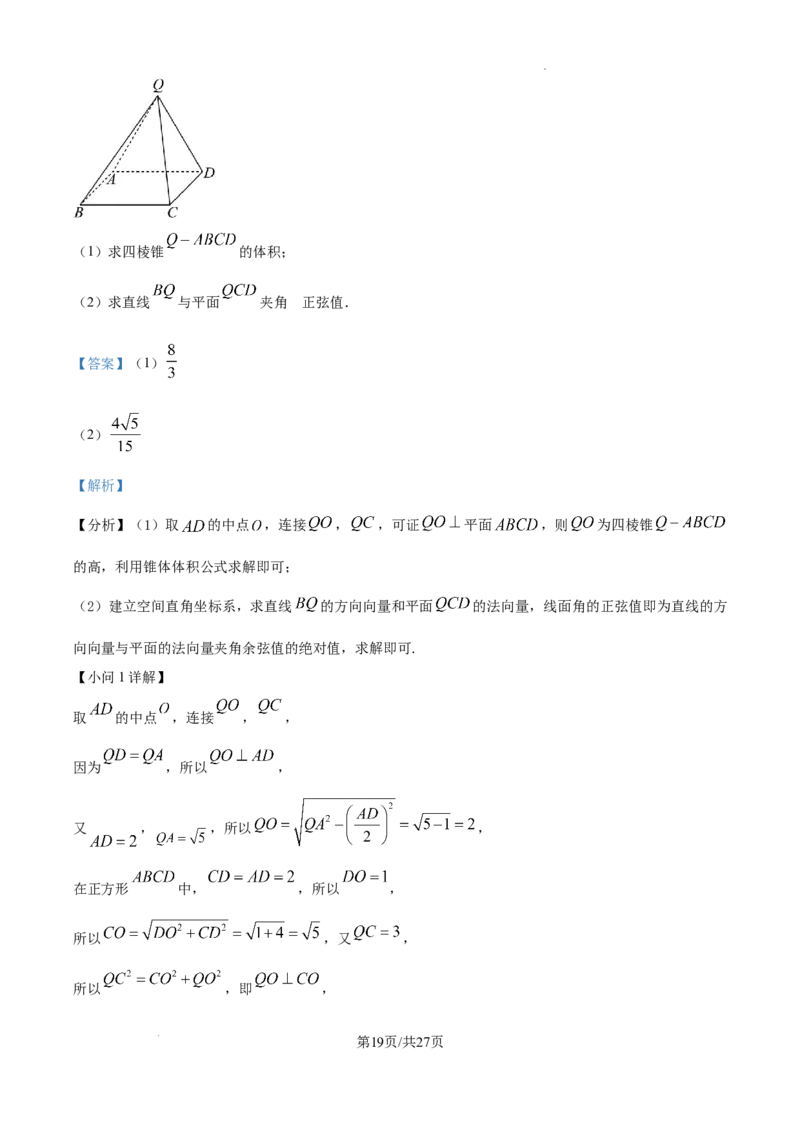
19. 在四棱锥 中,底面 是正方形,若 , , ,
第18页/共27页
学科网(北京)股份有限公司(1)求四棱锥 的体积;
的
(2)求直线 与平面 夹角 正弦值.
【答案】(1)
(2)
【解析】
【分析】(1)取 的中点 ,连接 , ,可证 平面 ,则 为四棱锥
的高,利用锥体体积公式求解即可;
(2)建立空间直角坐标系,求直线 的方向向量和平面 的法向量,线面角的正弦值即为直线的方
向向量与平面的法向量夹角余弦值的绝对值,求解即可.
【小问1详解】
取 的中点 ,连接 , ,
因为 ,所以 ,
又 , ,所以 ,
在正方形 中, ,所以 ,
所以 ,又 ,
所以 ,即 ,
第19页/共27页
学科网(北京)股份有限公司又 , 平面 , 平面 ,
所以 平面 ,
所以四棱锥 的体积为 ;
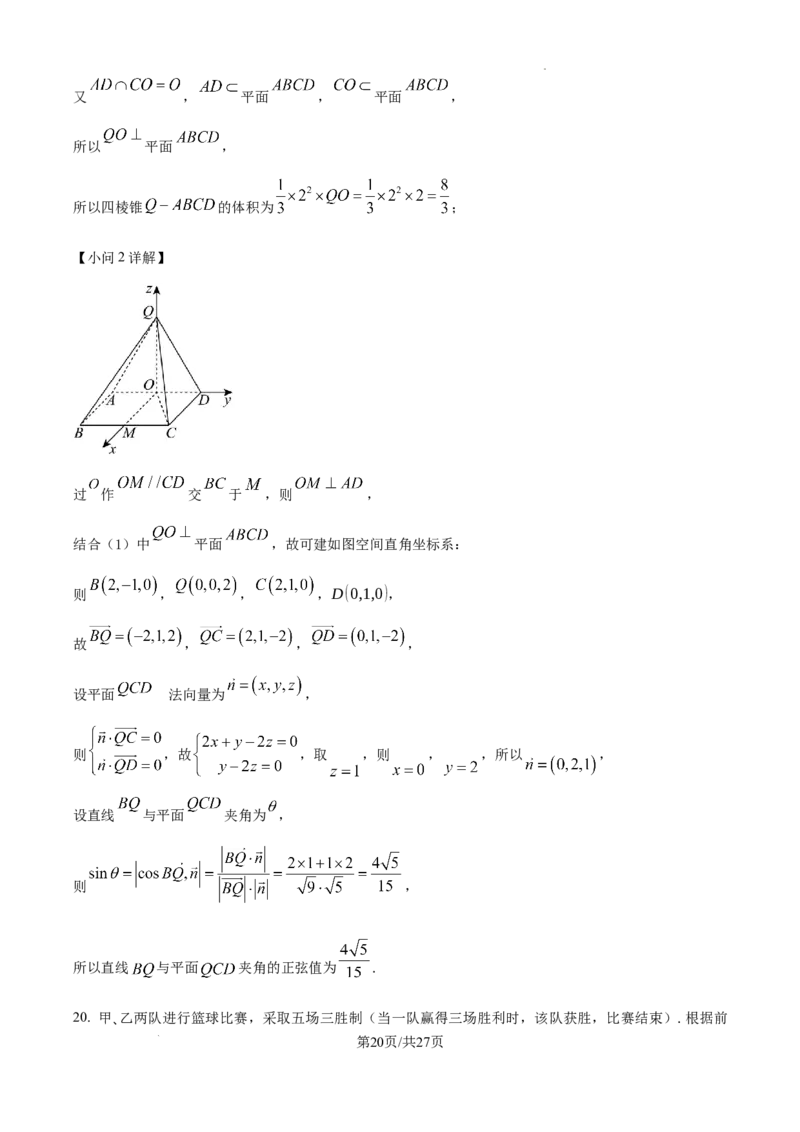
【小问2详解】
过 作 交 于 ,则 ,
结合(1)中 平面 ,故可建如图空间直角坐标系:
则 , , ,D(0,1,0),
故 , , ,
设平面 的法向量为 ,
则 ,故 ,取 ,则 , ,所以 ,
设直线 与平面 夹角为 ,
则 ,
所以直线 与平面 夹角的正弦值为 .
20. 甲、乙两队进行篮球比赛,采取五场三胜制(当一队赢得三场胜利时,该队获胜,比赛结束).根据前
第20页/共27页
学科网(北京)股份有限公司期比赛成绩,甲队的主客场安排依次为“主主客客主”,设甲队主场取胜的概率为0.6,客场取胜的概率为
0.5,且各场比赛结果相互独立.
(1)在比赛进行4场结束的条件下,求甲队获胜的概率;
(2)赛事主办方需要预支球队费用 万元.假设主办方在前3场比赛每场收入100万元,之后的比赛每场
收入200万元.主办方该如何确定 的值,才能使其获利(获利=总收入 预支球队费用)的期望高于 万
元?
【答案】(1)
(2)
【解析】
【分析】(1)先求出比赛4场结束的概率,然后利用条件概率公式即可解答;
(2)先由题意列出比赛收入的分布列,从而求出期望值,进而根据题意确定 的值.
【小问1详解】
记事件 为“比赛进行4场结束”;事件 为“甲最终获胜”,
事件 表示“第 场甲获胜” ,
事件 为“比赛进行4场结束甲获胜”;事件 为“比赛进行4场结束乙获胜”.
则 ,
因为各场比赛结果相互独立,
所以
,
,
因为 互斥,所以 .
又因为 ,
第21页/共27页
学科网(北京)股份有限公司所以由条件概率计算公式得 .
【小问2详解】
设主办方本次比赛总收入为 万元,
由题意: 的可能取值为: .
,
,
,
则随机变量 的分布列为:
300 500 700
0.3
0.26 0.37
7
所以 .
设主办方本次比赛获利为 万元,则 ,
所以 ,
由题意: ,
所以预支球队的费用应小于261万元.
21. 抛物线 : ,双曲线 : 且离心率 ,过曲线 下支上的一点
作 的切线,其斜率为 .
(1)求 的标准方程;
第22页/共27页
学科网(北京)股份有限公司(2)直线 与 交于不同的两点 , ,以PQ为直径的圆过点 ,过点N作直线 的垂线,垂足
为H,则平面内是否存在定点D,使得DH为定值,若存在,求出定值和定点D的坐标;若不存在,请说
明理由.
【答案】(1) ;
(2)存在, ,定点 .
【解析】
【分析】(1)写出切线方程并与抛物线方程联立求出点M坐标,再结合离心率求出双曲线方程作答.
(2)当直线PQ不垂直于y轴时,设出直线方程并与 的方程联立,借助韦达定理及向量数量积求出直
线PQ过定点E,直线PQ垂直于y轴,验证也过定点E,取线段EN中点即可作答.
【小问1详解】
切线方程为 ,即 ,由 消去y并整理得:
,则 ,解得 ,即 ,
由 离 心 率 得 , 即 , 双 曲 线 , 则
,
所以双曲线 的标准方程为: .
【小问2详解】
第23页/共27页
学科网(北京)股份有限公司当直线PQ不垂直于y轴时,设直线 方程为 , , ,
由 消去x并整理得: ,
有 , , ,
, ,因以 为直径的圆过点 ,则当P,Q与N都不重合时,
有 ,
,当P,Q之一与N重合时, 成立,于是得 ,
则有
,即 ,
整理得 ,即 ,
因此 ,解得 或 ,均满足 ,
当 时,直线 : 恒过 ,不符合题意,
当 时,直线 : ,即 恒过 ,符合题意,
当直线PQ垂直于y轴时,设直线 ,由 解得 ,
因以 为直径的圆过点 ,则由对称性得 ,解得 ,直线 过点
第24页/共27页
学科网(北京)股份有限公司,
于是得直线 过定点 ,取EN中点 ,因 于H,从而 ,
所以存在定点D,使得 为定值 ,点 .
【点睛】思路点睛:与圆锥曲线相交的直线过定点问题,设出直线的斜截式方程,与圆锥曲线方程联立,
借助韦达定理求出直线斜率与纵截距的关系即可解决问题.
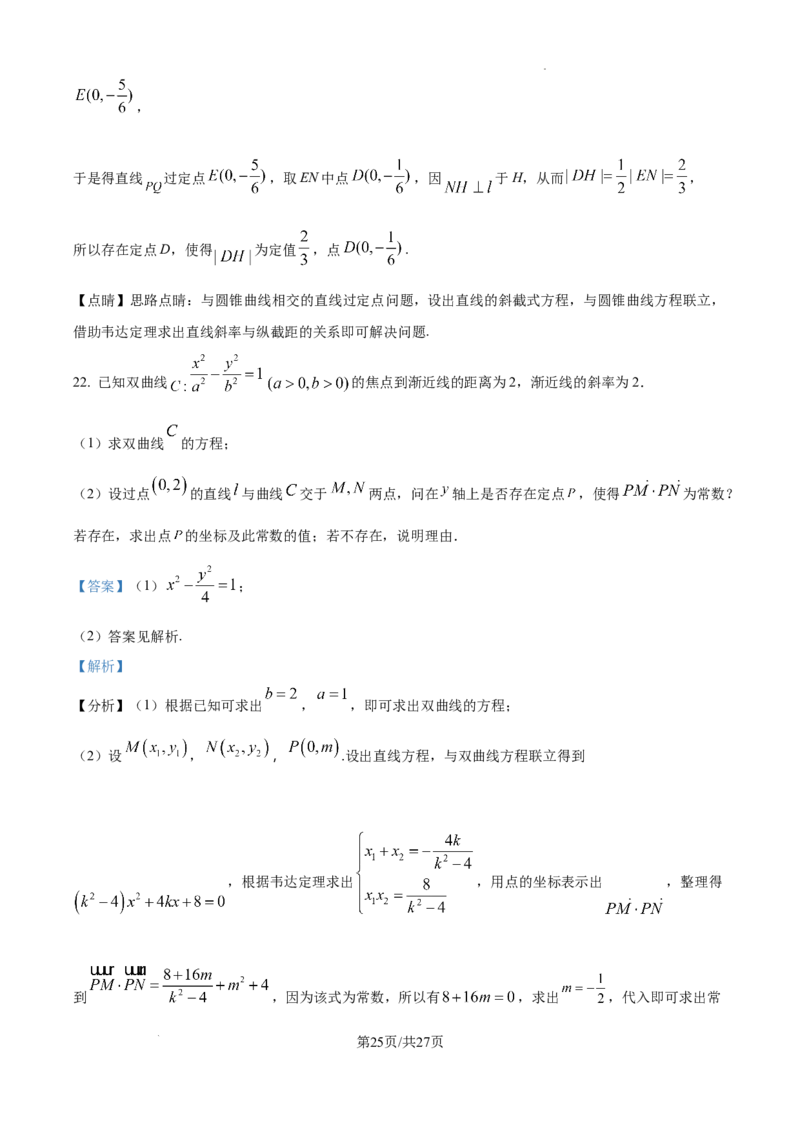
22. 已知双曲线 的焦点到渐近线的距离为2,渐近线的斜率为2.
(1)求双曲线 的方程;
(2)设过点 的直线 与曲线 交于 两点,问在 轴上是否存在定点 ,使得 为常数?
若存在,求出点 的坐标及此常数的值;若不存在,说明理由.
【答案】(1) ;
(2)答案见解析.
【解析】
【分析】(1)根据已知可求出 , ,即可求出双曲线的方程;
(2)设 , , .设出直线方程,与双曲线方程联立得到
,根据韦达定理求出 ,用点的坐标表示出 ,整理得
到 ,因为该式为常数,所以有 ,求出 ,代入即可求出常
第25页/共27页
学科网(北京)股份有限公司数.
【小问1详解】
由已知可得,双曲线的渐近线方程为 ,双曲线焦点 , .
则 到渐近线 ,即 的距离为 ,所以 ,
又渐近线的斜率为2,即 ,所以 ,
所以双曲线 的方程为 .
【小问2详解】
由已知可得,直线 的斜率存在,设斜率为 ,则 .
联立直线 的方程与双曲线的方程 可得, ,
设 , , .
当 ,即 时,此时直线 与双曲线的渐近线平行,不满足题意,所以 , .
,解得 ,且 .
由韦达定理可得, ,且 , .
又 , ,
则 ,
因为 , ,
第26页/共27页
学科网(北京)股份有限公司所以
,
要使 为常数,则 应与 无关,
即应有 ,解得 ,此时 是个常数,这样的点 存在.
所以,在 轴上存在定点 的坐标为 ,使得 为常数.
第27页/共27页
学科网(北京)股份有限公司