文档内容
河南省信阳高级中学北湖校区
2024-2025 学年高二上期开学测试
数学答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C D B D B B C ACD AD BC
题号 11 12
答案 ABC BD
13.3 15.8
16.
14.
17.(1)
(2) 或 .
(3)
【分析】(1)利用夹角公式可求夹角的余弦值.
(2)利用向量垂直的坐标形式可求参数的值.
(3)利用共线向量定理可求参数的值.
【详解】(1) , ,
故 .
(2)由(1)可得
, ,
因为向量 , 垂直,故 ,
整理得到: ,故 或 .
(3)由(1)可得 不共线,故 , 均不为零向量,
若向量 , 平行,则存在非零常数 ,使得 ,
1
学科网(北京)股份有限公司整理得到: ,
因为 不共线,故 ,故 或 ,
故 .
18.(1)
(2)
(3)
【分析】(1)利用频率之和为 求解即可;
(2)先判断中位数所在区间,再利用中位数的定义列式求解即可;
(3)先利用分层抽样确定男女生人数,再利用列举法与古典概型的概率公式求
解即可.
【详解】(1)依题意,得 ,解得 ;
(2)因为 , ,
所以中位数在 间,设为 ,
则 ,解得 .
(3)依题意,因为满意度评分值在 的男生数与女生数的比为 ,
按照分层抽样的方法在其中随机抽取5人,则抽中男生3人,女生2人,依次
分别记为 ,
对这5人依次进行座谈,前2人的基本事件有: , , , , ,
, , , , ,共10件,
2
学科网(北京)股份有限公司设“前2人均为男生”为事件A,其包含的基本事件有: , , ,共
3个,
所以 .
19.(1)
(2)
【分析】(1)求出交点坐标,进而得到半径,得到圆的标准方程;
(2)由垂径定理得到圆心 到直线 的距离,利用点到直线距离公
式求出答案.
【详解】(1)联立 ,解得 ,
故半径为 ,
故圆C的标准方程为 ;
(2)设圆心 到直线 的距离为 ,
则由垂径定理得 ,
解得 ,即 ,解得 ,
故直线l的方程为 ,即 .
20.(1)
(2)4
【分析】(1)利用正弦定理边角互化,转化为三角函数求角;
(2)首先根据三角形的面积公式,求得 ,再根据余弦定理求得
3
学科网(北京)股份有限公司,再根据中线向量关系, 利用数量积公式,即可求解.
【详解】(1) ,∴由正弦定理得: ,
,∴ ,
∴ ,即 ,
,∴ ,
∴ ,
(2) , ,
在 中,由余弦定理 得
,所以 ,
设 的中点为 ,则 ,
两边同时平方得:
=
所以 ,所以 .
21.(1)证明见解析;
(2) .
【分析】(1)根据题意易证 平面 ,从而证得 ;
(2)由题可证 平面 ,所以以点 为原点, 所在直线分别为
4
学科网(北京)股份有限公司轴,建立空间直角坐标系,再求出平面 的一个法向量,根据二面
角的向量公式以及同角三角函数关系即可解出.
【详解】(1)连接 ,因为E为BC中点, ,所以 ①,
因为 , ,所以 与 均为等边三角形,
,从而 ②,由①②, , 平面 ,
所以, 平面 ,而 平面 ,所以 .
(2)不妨设 , , .
, ,又 , 平面
平面 .
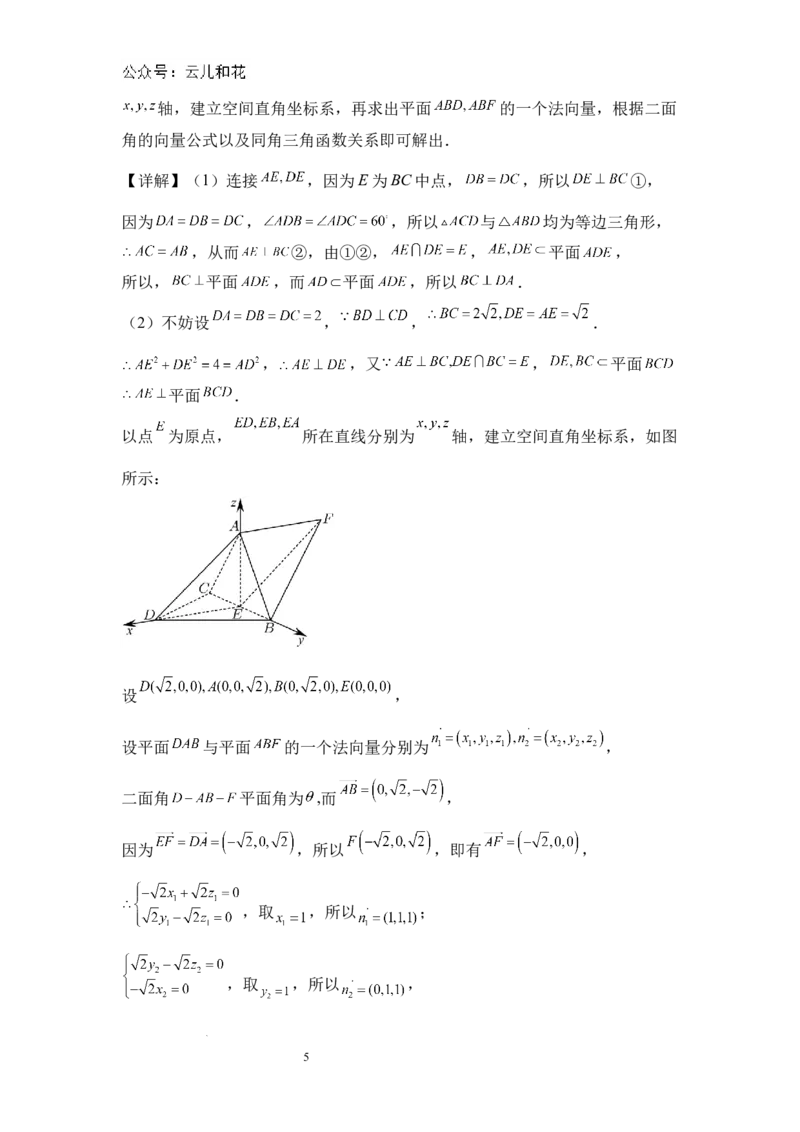
以点 为原点, 所在直线分别为 轴,建立空间直角坐标系,如图
所示:
设 ,
设平面 与平面 的一个法向量分别为 ,
二面角 平面角为 ,而 ,
因为 ,所以 ,即有 ,
,取 ,所以 ;
,取 ,所以 ,
5
学科网(北京)股份有限公司所以, ,从而 .
所以二面角 的正弦值为 .
22.(1) (2)
【分析】(1)先设甲发球甲赢为事件A,乙发球甲赢为事件B,然后分析这4
个球的发球者及输赢者,即可得到所求事件的构成,利用相互独立事件的概率
计算公式即可求解;
(2)先将所求事件分成甲赢与乙赢这两个互斥事件,再分析各事件的构成,利
用互斥事件和相互独立事件的概率计算公式即可求得概率.
【详解】(1)设甲发球甲赢为事件A,乙发球甲赢为事件B,该局打4个球甲
赢为事件C,
由题知, , ,∴ ,
∴ ,
∴该局打4个球甲赢的概率为 .
(2)设该局打5个球结束时甲赢为事件D,乙赢为事件E,打5个球结束为事
件F,易知D,E为互斥事件,
, , ,
∴
,
,
∴ ,
6
学科网(北京)股份有限公司∴该局打5个球结束的概率为 .
7
学科网(北京)股份有限公司