2006年上海高考数学试卷（文）（自主命题）（空白卷）_数学高考真题试卷_旧1990-2007·高考数学真题_1990-2007·高考数学真题·PDF_上海

绝密★启用前 2006年普通高等学校招生全国统一考试（上海卷） 数学试卷(文史类) （满分150分，考试时间120分钟） 考生注意 1.本场考试时间120分钟，试卷共4页，满分150分，答题纸共2页. 2.作答前，在答题纸正面填写姓名、准考证号，反面填写姓名，将核对后的条形码贴在答 题纸指定位置. 3.所有作答务必填涂或书写在答题纸上与试卷题号对应的区域，不得错位.在试卷上作答 一律不得分. 4.用2B铅笔作答选择题，用黑色字迹钢笔、水笔或圆珠笔作答非选择题. 一、填空题（本大题满分48分）本大题共有12题，只要求直接填写结果，每个 空填对得4分，否则一律得零分。 1、已知A{1,3,m}，集合B{3,4}，若B A,则实数m ___ 。 2、已知两条直线l :ax3y30,l :4x6y10.若l //l ，则a ____. 1 2 1 2 3、若函数 f(x)ax(a0,且a1)的反函数的图像过点(2,1)，则a ___。 n(n2 1) 4、计算：lim  ______。 6n31 n 5、若复数z满足z (m2)(m1)i（i为虚数单位），其中mR则 z  ____ 。 6、函数y sinxcosx的最小正周期是_________。 7、已知双曲线中心在原点，一个顶点的坐标为(3,0),且焦距与虚轴长之比为 5:4，则双曲线的标准方程是____________________. 8、方程log (x2 10)1log x的解是_______. 3 3 x y30  x2y50 9、已知实数x,y满足  ，则y2x的最大值是_________. x0   y0 第1页 | 共6页10、在一个小组中有8名女同学和4名男同学，从中任意地挑选2名同学担任交通 安全宣传志愿者，那么选到的两名都是女同学的概率是______（结果用分数表 示）。 11、若曲线 y 2x 1与直线y b没有公共点，则b的取值范围是_________. 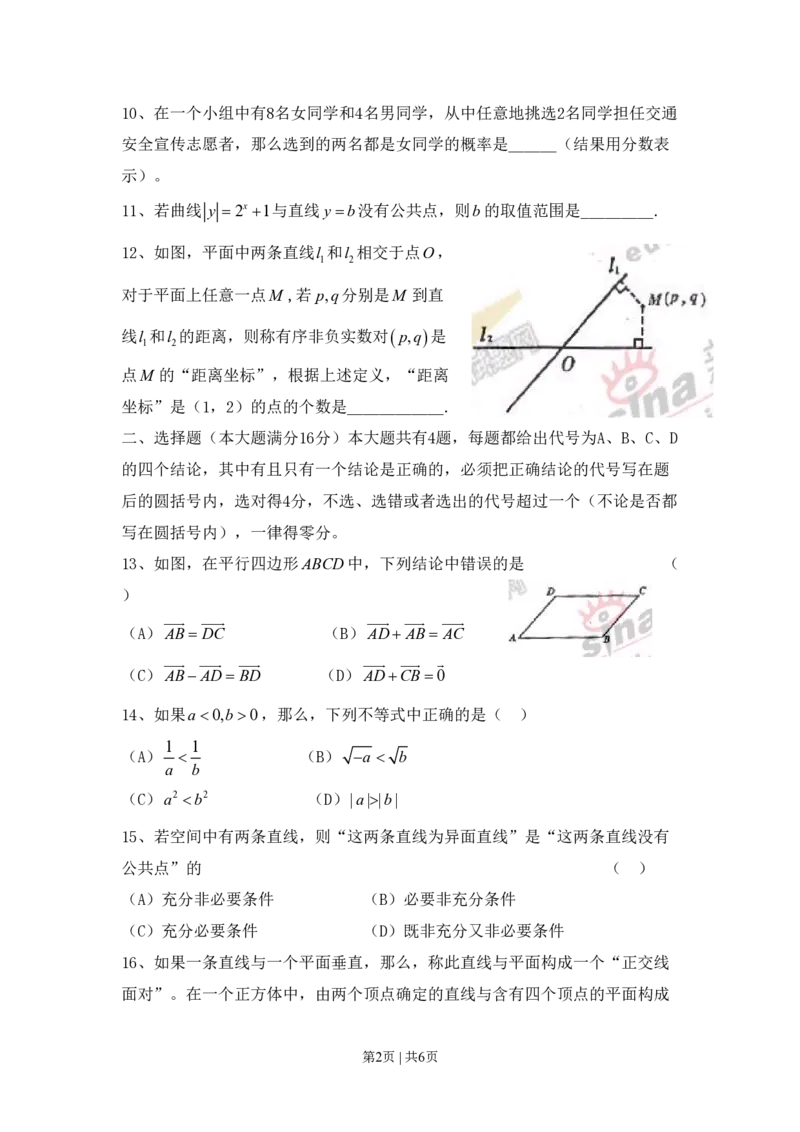12、如图，平面中两条直线l 和l 相交于点O， 1 2 对于平面上任意一点M ,若 p,q分别是M 到直 线l 和l 的距离，则称有序非负实数对p,q是 1 2 点M 的“距离坐标”，根据上述定义，“距离 坐标”是（1，2）的点的个数是____________. 二、选择题（本大题满分16分）本大题共有4题，每题都给出代号为A、B、C、D 的四个结论，其中有且只有一个结论是正确的，必须把正确结论的代号写在题 后的圆括号内，选对得4分，不选、选错或者选出的代号超过一个（不论是否都 写在圆括号内），一律得零分。 13、如图，在平行四边形ABCD中，下列结论中错误的是 （ ）      （A）AB DC （B）AD AB AC       （C）ABAD BD （D）ADCB0 14、如果a0,b0，那么，下列不等式中正确的是（ ） 1 1 （A）  （B） a  b a b （C）a2 b2 （D）|a||b| 15、若空间中有两条直线，则“这两条直线为异面直线”是“这两条直线没有 公共点”的 （ ） （A）充分非必要条件 （B）必要非充分条件 （C）充分必要条件 （D）既非充分又非必要条件 16、如果一条直线与一个平面垂直，那么，称此直线与平面构成一个“正交线 面对”。在一个正方体中，由两个顶点确定的直线与含有四个顶点的平面构成 第2页 | 共6页的“正交线面对”的个数是 （A）48 （B） 18 （C） 24 （D）36 三、解答题（本大题满分86分）本大题共有6题，解答下列各题必须写出必要的 步骤。 17、（本题满分12分）   sin    5  4 已知是第一象限的角，且cos ，求 的值。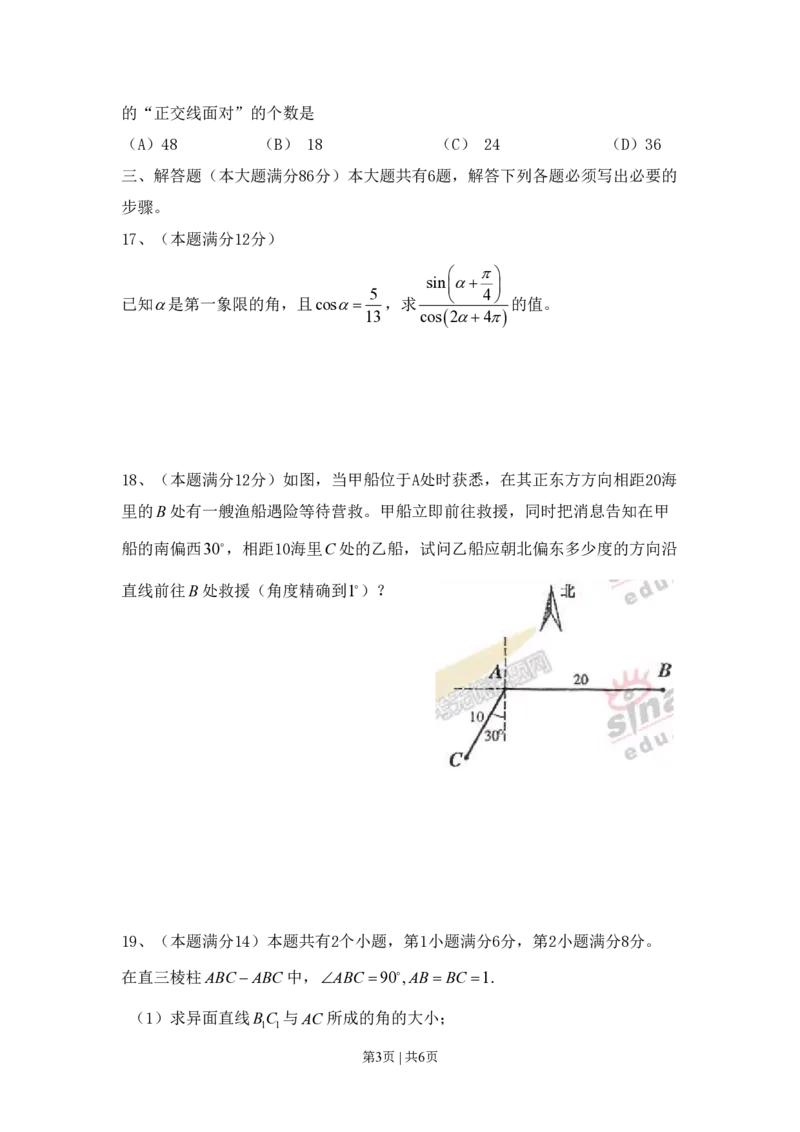 13 cos24 18、（本题满分12分）如图，当甲船位于A处时获悉，在其正东方方向相距20海 里的B处有一艘渔船遇险等待营救。甲船立即前往救援，同时把消息告知在甲 船的南偏西30，相距10海里C处的乙船，试问乙船应朝北偏东多少度的方向沿 直线前往B处救援（角度精确到1）？ 19、（本题满分14）本题共有2个小题，第1小题满分6分，第2小题满分8分。 在直三棱柱ABCABC中，ABC 90,AB BC 1. （1）求异面直线BC 与AC所成的角的大小； 1 1 第3页 | 共6页（2）若AC与平面ABCS所成角为45，求三棱锥A ABC的体积。 1 1 20、（本题满分14）本题共有2个小题，第1小题满分6分，第2小题满分8分。设 数列{a }的前n项和为S ，且对任意正整数n，a S 4096。 n n n n （1）求数列{a }的通项公式 n （2）设数列{log a }的前n项和为T ,对数列T ，从第几项起T 509？ 2 n n n n 21、本题共有3个小题，第1小题满分4分，第2小题满分6分，第3小题满分6分。 已知在平面直角坐标系xOy中的一个椭圆，它的中心在原点，左焦点为  1 F( 3,0),右顶点为D(2,0),设点A 1, .    2 （1）求该椭圆的标准方程； （2）若P是椭圆上的动点，求线段PA中点M 的 第4页 | 共6页轨迹方程； （3）过原点O的直线交椭圆于点B,C ，求ABC面积的最大值。 22（本题满分18分）本题共有3个小题，第1小题满分4分，第2小题满分8分，第 3小题满分6分。 a  已知函数y  x 有如下性质：如果常数a 0，那么该函数在 0, a上是  x  减函数，在 a, 上是增函数。  2b （1）如果函数y  x (x0)在0,4上是减函数，在4,上是增函数，求 x b的值。 c （2）设常数c1,4，求函数 f(x) x (1 x2)的最大值和最小值； x c （3）当n是正整数时，研究函数g(x) xn  (c0)的单调性，并说明理由。 xn 第5页 | 共6页第6页 | 共6页