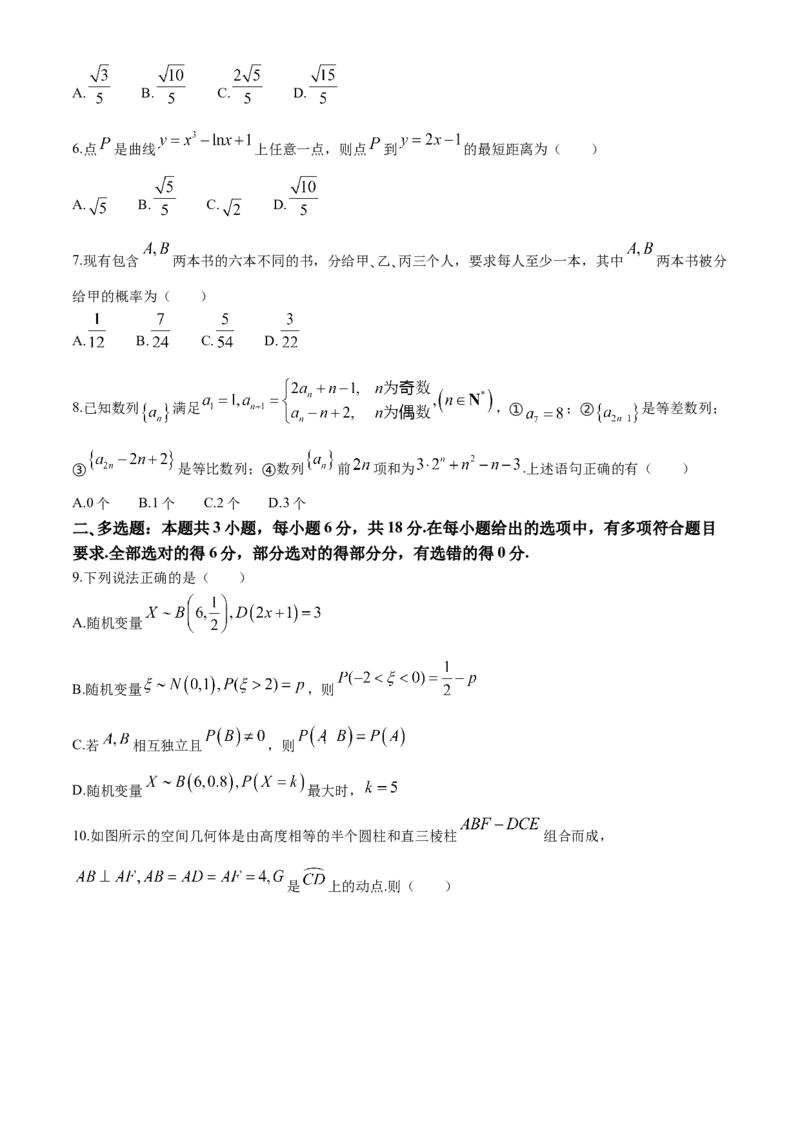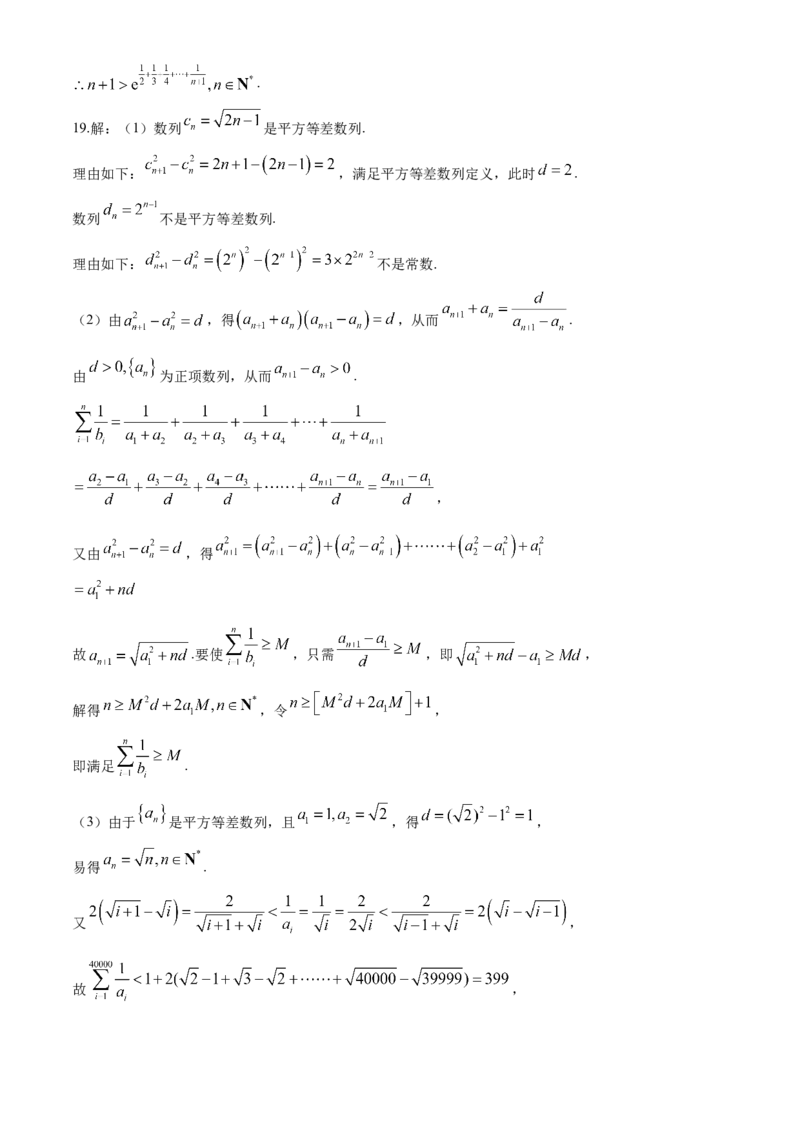文档内容
漯河市 2023-2024 学年下学期期末质量监测
高二数学
一、选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项
是符合要求的、
1.已知等差数列 的前 项和为 ,且 也为等差数列, ,则 ( )
A.-1 B.1 C.2 D.3
2.已知双曲线 的离心率为2,则该双曲线的渐近线方程为( )
A. B.
C. D.
3.直线 与圆 交于 两点,则弦 的长( )
A. B. C. D.
4.甲乙两人独立地对同一目标各射击一次,命中率分别为 和 ,在目标被击中的情况下,甲乙同时击中
目标的概率为( )
A. B. C. D.
5.已知如图所示的几何体中,底面 是边长为4的正三角形,侧面 是长方形, ,平面
平面 为棱 上一点, ,且 ,则 与平面 所成角
的正弦值为( )A. B. C. D.
6.点 是曲线 上任意一点,则点 到 的最短距离为( )
A. B. C. D.
7.现有包含 两本书的六本不同的书,分给甲、乙、丙三个人,要求每人至少一本,其中 两本书被分
给甲的概率为( )
A. B. C. D.
8.已知数列 满足 ,① ;② 是等差数列;
③ 是等比数列;④数列 前 项和为 .上述语句正确的有( )
A.0个 B.1个 C.2个 D.3个
二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目
要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.下列说法正确的是( )
A.随机变量
B.随机变量 ,则
C.若 相互独立且 ,则
D.随机变量 最大时,
10.如图所示的空间几何体是由高度相等的半个圆柱和直三棱柱 组合而成,
是 上的动点.则( )A. 为 的中点时,平面 平面
B. 为 的中点时, 平面
C.存在点 ,使得三棱锥 体积是8
D.存在点 ,使得直线 与平面 所成的角为
11.我们在解析几何学习过程中知道椭圆、双曲线定义分别是到两定点距离之和、距离之差的绝对值等于某个
定值.天文学家卡西尼在研究土星及其卫星运行规律时发现了到两定点距离之积为常数的点的轨迹,我们称
之为卡西尼卵形线.已知两定点 ,动点 满足 ,设 的轨迹为
曲线 ,则下列命题正确的是( )
A.曲线 过原点
B. 的横坐标最大值是
C. 的纵坐标最大值是
D.
三、填空题:本题共3小题,每小题5分,共15分.
12.已知 的展开式的各二项式系数之和为512,则其展开式的常数项的值为__________.
13.已知 是函数 的零点,则 __________.
14.半径为2的球内切于一个圆锥,则该圆锥的侧面积的最小值为__________.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(本小题满分13)为了丰富校园文化生活,学校增设了两门全新的课程 ,学生根据自己的兴趣爱
好在这两门课程中任选一门进行学习.学校统计了学生的选课情况,得到如下表格.
选择课程 选择课程男生 40 60
女生 20 80
(1)根据上表,依据小概率值 的 独立性检验,能否据此推断选择课程与性别有关?
(2)现从男生的样本中,按比例分配分层抽样的方法选出10人组成一个小组,再从这10名男生中抽取3
人做问卷调查,求这3人中选择课程 的人数比选择课程 的人数多的概率.
附: .
0.05 0.01 0.005 0.001
3.841 6.635 7.879 10.828
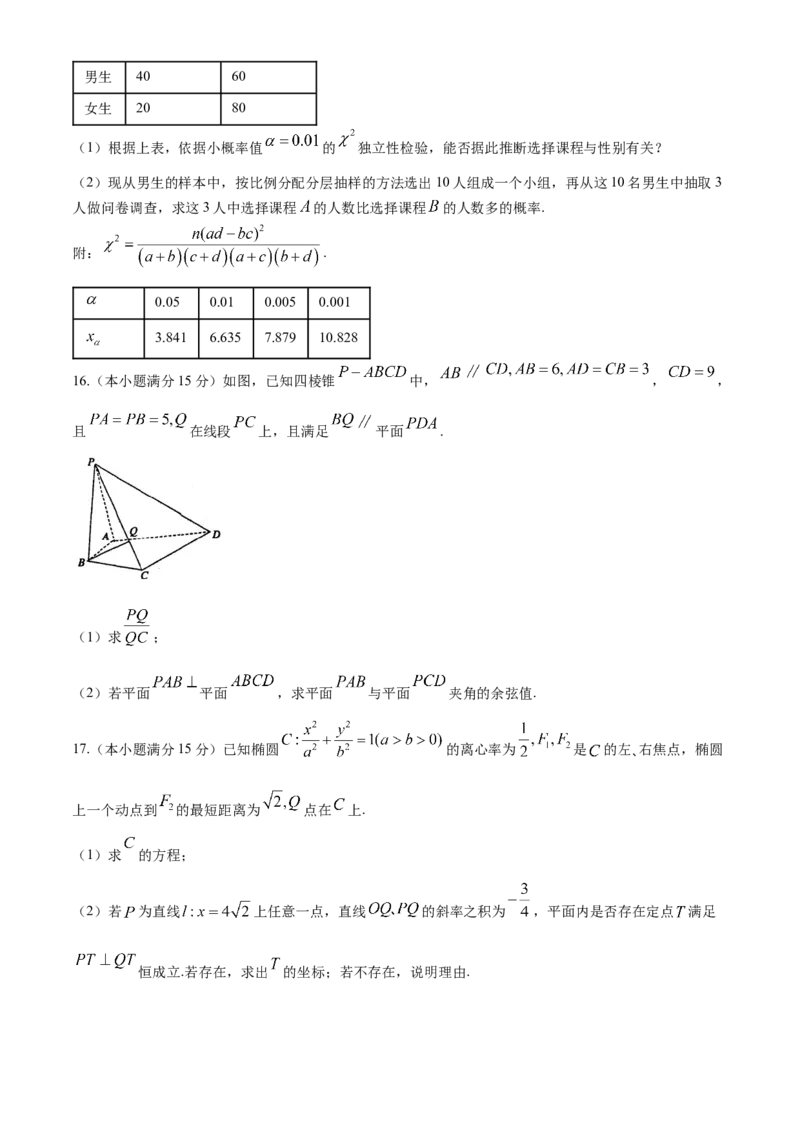
16.(本小题满分15分)如图,已知四棱锥 中, , ,
且 在线段 上,且满足 平面 .
(1)求 ;
(2)若平面 平面 ,求平面 与平面 夹角的余弦值.
17.(本小题满分15分)已知椭圆 的离心率为 是 的左、右焦点,椭圆
上一个动点到 的最短距离为 点在 上.
(1)求 的方程;
(2)若 为直线 上任意一点,直线 的斜率之积为 ,平面内是否存在定点 满足
恒成立.若存在,求出 的坐标;若不存在,说明理由.18.(本小题满分17分)已知函数 .
(1)求 的单调区间;
(2)对任意的 恒成立,求 的值;
(3)证明: .
19.(本小题满分17分)正项数列 满足:对于 ,其中 为非零常数,则称数列
为平方等差数列.记 .
(1)判断无穷数列 和 是否是平方等差数列,若是求出 ,若不是,说明理由;
(2)若 是平方等差数列且 ,证明:任意的正常数 ,存在正整数 ,使得 .
(3)若 是平方等差数列, ,令 是不大于 的最大整数,求 .
漯河市 2023-2024 学年下学期期末质量监测
高二数学参考答案
(解答题方法不唯一,请阅卷前先做题,然后同组老师讨论,细化评分标准;确保阅卷过程
中宽严适度,始终如一,让努力学习、认真答题的学生有获得感.辛苦大家!)
一、单项选择题:
1.C 2.D 3.B 4.A 5.D 6.B 7.C 8.D
二、多项选择题:
9.BCD 10.ABC 11.ABD
三、填空题:
12.84 13.1 14.
四、解答题:
15.解:(1)零假设 :选择课程与性别无关,根据小概率值 的 独立性检验,推断 不成立,
即认为选择课程与性别有关.
(2)由表可知,男生中选 课程的人数占 ,选 课程的人数占 ,
故10名男生中,选择课程 的人数为 ,选择课程 的人数为
则所求的概率为 .
16.(1)过点 作 交 于 ,连接 ,由于 平面 ,由线面平行性质知
,又 四边形 为平行四边形.所以 ,
则 .
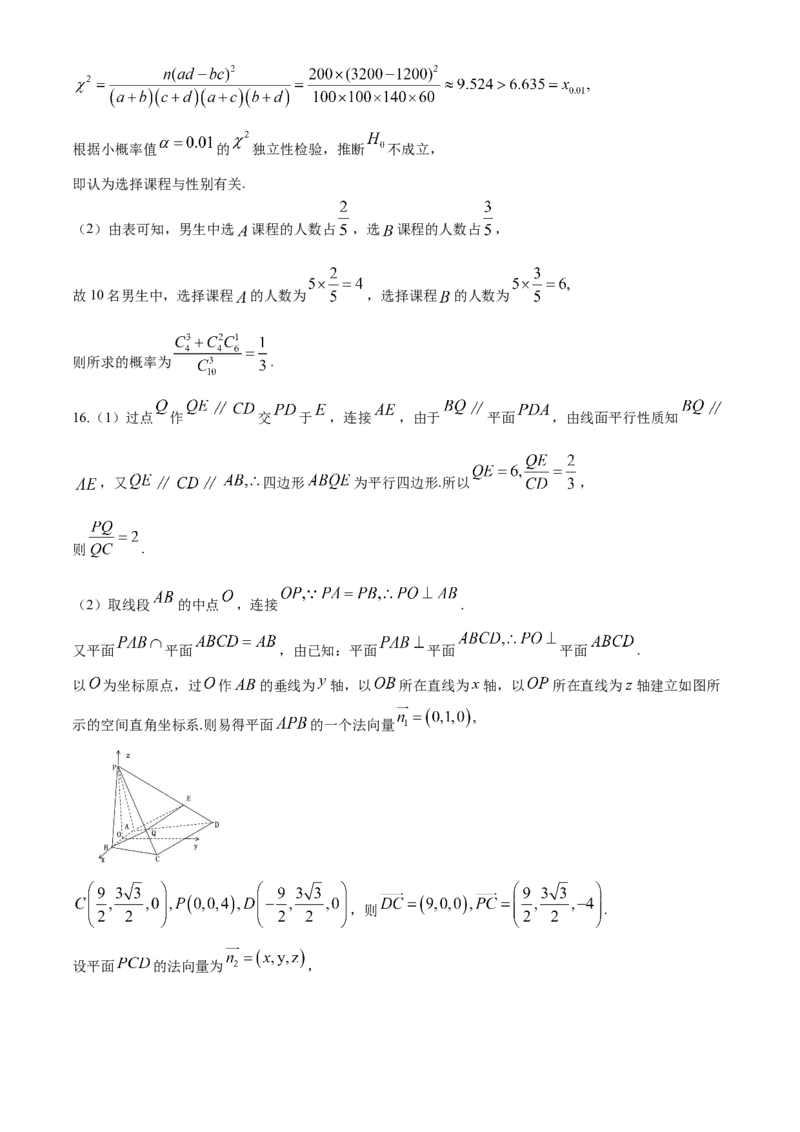
(2)取线段 的中点 ,连接 .
又平面 平面 ,由已知:平面 平面 平面 .
以 为坐标原点,过 作 的垂线为 轴,以 所在直线为 轴,以 所在直线为 轴建立如图所
示的空间直角坐标系.则易得平面 的一个法向量
,则 .
设平面 的法向量为 ,则
令 ,可得 .
设平面 与平面 夹角为 .
故平面 与平面 夹角的余弦值为 .
17.解:(1)由已知: ,
椭圆 的方程为 .
(2)设 ,则 ,
整理得 ,又 在 上,
.
①
由对称性知:若存在点 满足 恒成立,则 在 轴上,设 ,则 ,
即 ,
将①代入,得: ,
适合题意.即存在定点 满足 恒成立.
18.解:(1) 的定义域为 ,
当 时,令 ,得 的单调递增区间为 ;令 ,得 的单调递减区间为 .
当 时,令 ,得 的单调递增区间为 ;
令 ,得 的单调递减区间为 .
(2) 等价于 ,
令 ,则不等式等价于 ,
当 ,则 在 上单调递减, 时 不合题意;
当 ,令 得 的递增区间为 ,
令 得 的递减区间为 ,
若 ,则当 时, ,不合题意;
若 ,适合题意;
若 ,则当 时, ,不合题意;
综上, .
(3)由(2)知:当 时,有 ,当且仅当 时等号成立.
时, ,
,
,
,即 ,.
19.解:(1)数列 是平方等差数列.
理由如下: ,满足平方等差数列定义,此时 .
数列 不是平方等差数列.
理由如下: 不是常数.
(2)由 ,得 ,从而 .
由 为正项数列,从而 .
,
又由 ,得
故 .要使 ,只需 ,即 ,
解得 ,令 ,
即满足 .
(3)由于 是平方等差数列,且 ,得 ,
易得 .
又 ,
故 ,所以 .