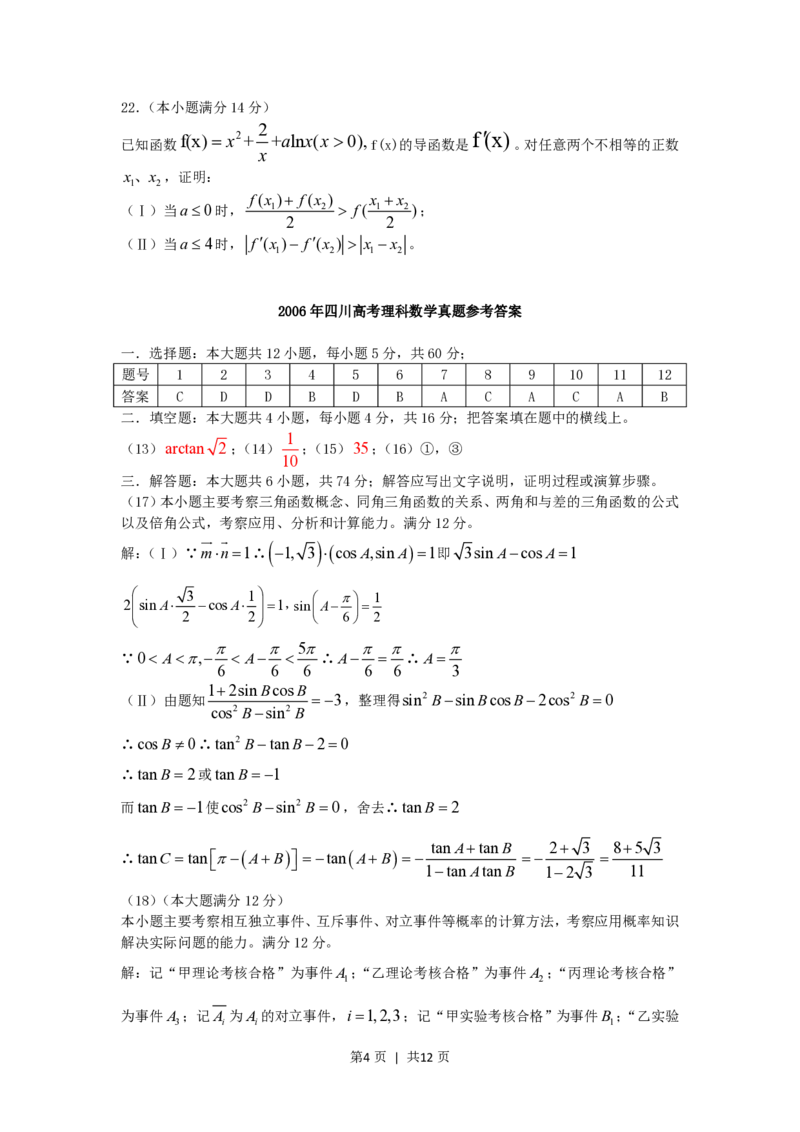2006年四川高考理科数学真题及答案_数学高考真题试卷_旧1990-2007·高考数学真题_1990-2007·高考数学真题·PDF_四川

2006 年四川高考理科数学真题及答案
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。第Ⅰ卷1至2页。第Ⅱ卷3
到8页。考试结束后，将本试卷和答题卡一并交回。
第Ⅰ卷
注意事项：
1．答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上。
2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑。如需改动，用橡
皮擦干净后，再选涂其它答案标号。不能答在试题卷上。
3．本卷共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是
符合题目要求的。
参考公式：
如果事件A、B互斥，那么球是表面积公式
P(AB)  P(A)P(B) S  4R2
如果事件A、B相互独立，那么其中R表示球的半径
P(AB)  P(A)P(B)球的体积公式
4
如果事件A在一次试验中发生的概率是P，那么V  R3
3
n次独立重复试验中恰好发生k次的概率其中R表示球的半径
P (k) CkPk(1P)nk
n n
一、选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有
一项是符合题目要求的。
1.已知集合A=  x|x25x60  ,Bx| 2x1 3,则集合A B＝

（A）x|2 x3 （B）x|2x3 （C）x|2x3 （D）x|1x3
2.复数13i3
的虚部为
（A）3 （B）－3 （C）2 （D）－2.
2x3,x1
3.已知 f(x) ,下面结论正确的是
2, x1
（A）f(x)在x=1处连续 （B）f(1)＝5 （C）lim f(x)2 （D）lim f(x)5
x1－ x1
4. 已 知 二 面 角 l的 大 小 为 600，
m、n为异面直线，且m，n，则m、n 所成的角为
（A）300 （B）600 （C）900 （D）1200
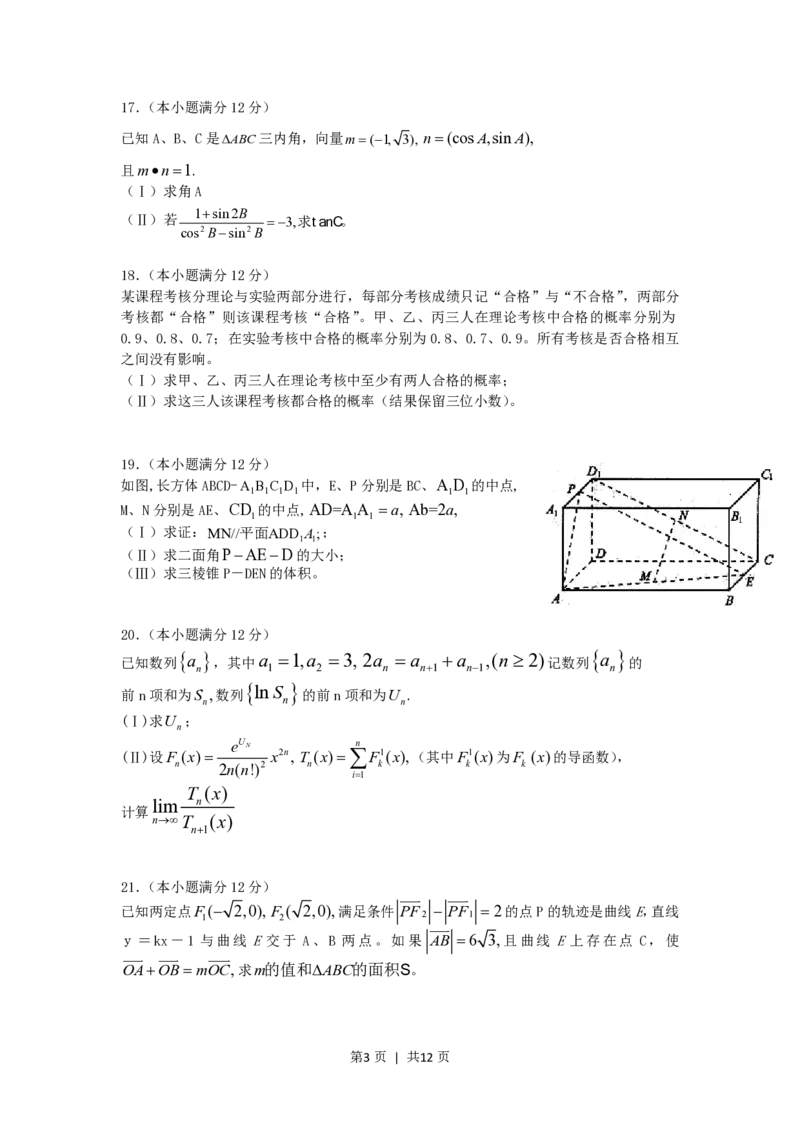
5.下列函数中，图像的一部分如右图所示的是
 
（A）ysin(x ) （B）ysin(2x )
6 6
 
（C）ycos(4x ) （D）ycos(2x )
3 6
6. 已知两定点 A(2,0), B(1,0),如果动点 P 满足条件
PA 2 PB,则点P的轨迹所包围的图形的面积等于

（A） （B）4 （C）8 （D）9
7.如图,已知正六边形PPPPPP ，下列向量的数量积中最大的是
1 2 3 4 5 6
       
（A）PP PP （B）PP PP （C）PP PP （D）PP PP
1 2 1 3 1 2 1 4 1 2 1 5 1 2 1 6
8.某厂生产甲产品每千克需用原料A和原料B分别为a、b 千克，生产
1 1
第1页 | 共12页乙产品每千克需用原料A和原料B分别为a、b 千克。甲、乙产品每千克可获利润分别为
2 2
d、d 元。月初一次性购进本月用原料A、B各c、c 千克。要计划本月生产甲、乙两种产
1 2 1 2
品各多少千克才能使月利润总额达到最大。在这个问题中，设全月生产甲、乙两种产品分别
为ｘ千克、ｙ千克，月利润总额为ｚ元，那么，用于求使总利润z d xd y最大的数学
1 2
模型中，约束条件为
a xa yc , a xb yc, a xa yc , axa yc,
 1 2 1  1 1 1  1 2 1  1 2 1
（A）   b 1 xb 2 yc 2 , （B）  a 2 xb 2 yc 2 , （C）   b 1 xb 2 yc 2 , （D）  b 1 xb 2 yc 2 ,
 x0,  x0,  x0,  x0,
 y0  y0  y0  y0
9.直线ｙ＝ｘ－3与抛物线y2  4x交于A、B两点，过A、B两点向抛物线的准线作垂线，
垂足分别为P、Q ，则梯形APQB的面积为
（A）48 （B）56 （C）64 （D）72.
10.已知球O半径为1，A、B、C三点都在球面上，A、B两点和A、C两点的球面距离都是
，B、C两点的球面距离是  ，则二面角BOAC的大小是
4 3
  
2
（A） （B） （C） （D）
4 3 2 3
11.设a、b、c分别为ABC的三内角A、B、C 所对的边，则a2 b(bc)是A=2B的
（A）充要条件（B）充分而不必要条件（C）必要而不充分条件（D）既不充分也不必要条件
12.从0到9这10个数字中任取3个数字组成一个没有重复数字的三位数，这个数不能被３
整除的概率为
（A）19 （B） 35 （C） 38 （D） 41
54 54 54 60
第Ⅱ卷（非选择题 共90分）
二、填空题：本大题共4小题，每小题4分，共16分。把答案填在题中横线上。
13.在三棱锥O-ABC中，三条棱OA、OB、OC两两互相垂直，且OA＝OB＝OC,M是AB的中点，
则OM与平面ABC所成角的大小是______________（用反三角函数表示）。
14.设离散型随机变量ξ可能取的值为1，2，3，4.P(ξ＝k)＝ak+b(k=1，2，3，4),又ξ的
数学期望Eξ＝3，则ａ＋ｂ＝______________。
x2 y2
15.如图把椭圆  1的长轴AB分成8分，过每个分点
25 16
作ｘ轴的垂线交椭圆的上半部分于P,P ,……P 七个点，F
1 2 7
是椭圆的一个焦点，则
PF  PF ...... PF ____________．
1 2 7
16.非空集合G关于运算满足：（1）对任意的a,bG,都有abG,(2)存在eG,都
有abba a,则称G关于运算为“融洽集”。现给出下列集合和运算：
①G＝｛非负整数｝，为整数的加法。
②G＝｛偶数｝，为整数的乘法。
③G＝｛平面向量｝，为平面向量的加法。
④G＝｛二次三项式｝，为多项式的加法。
⑤G＝｛虚数｝，为复数的乘法。
其中G关于运算为“融洽集”的是________。（写出所有“融洽集”的序号）
三.解答题共6个小题，共74分，解答时应写出必要的文字说明，证明过程或演算步骤.
第2页 | 共12页17．（本小题满分12分）
已知A、B、C是ABC三内角，向量m(1, 3), n(cosA,sinA),
且mn1.
（Ⅰ）求角A
1sin2B
（Ⅱ）若 3,求tanC。
cos2Bsin2B
18．（本小题满分12分）
某课程考核分理论与实验两部分进行，每部分考核成绩只记“合格”与“不合格”，两部分
考核都“合格”则该课程考核“合格”。甲、乙、丙三人在理论考核中合格的概率分别为
0.9、0.8、0.7；在实验考核中合格的概率分别为0.8、0.7、0.9。所有考核是否合格相互
之间没有影响。
（Ⅰ）求甲、乙、丙三人在理论考核中至少有两人合格的概率；
（Ⅱ）求这三人该课程考核都合格的概率（结果保留三位小数）。
19．（本小题满分12分）
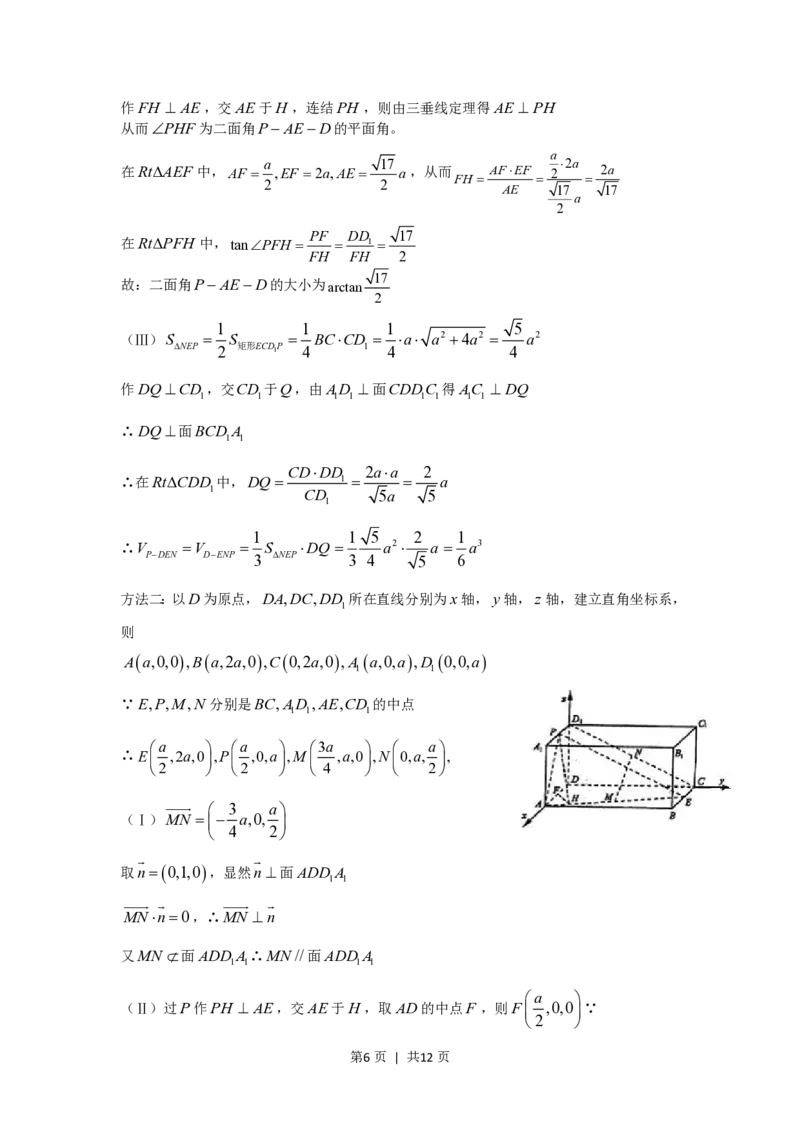
如图,长方体ABCD-A B C D 中，E、P分别是BC、A D 的中点,
1 1 1 1 1 1
M、N分别是AE、CD 的中点,AD=A A a, Ab=2a,
1 1 1
（Ⅰ）求证：MN//平面ADD A;；
1 1
（Ⅱ）求二面角PAED的大小；
（Ⅲ）求三棱锥P－DEN的体积。
20．（本小题满分12分）
已知数列
a 
，其中
a 1,a 3, 2a  a a ,(n  2)
记数列
a 
的
n 1 2 n n1 n1 n
lnS 
前n项和为S ,数列 的前n项和为U .
n n n
(Ⅰ)求U ；
n
eU N n
(Ⅱ)设F (x) x2n, T (x)F1(x),（其中F1(x)为F (x)的导函数），
n 2n(n!)2 n k k k
i1
T (x)
lim n
计算
nT (x)
n1
21．（本小题满分12分）
 
已知两定点F( 2,0), F ( 2,0),满足条件 PF  PF 2的点P的轨迹是曲线E，直线
1 2 2 1

ｙ＝kx－1 与曲线 E交于 A、B 两点。如果 AB 6 3,且曲线 E上存在点 C，使
  
OAOBmOC,求m的值和ABC的面积S。
第3页 | 共12页22．（本小题满分14分）
2
f(x)  x2+ +alnx(x 0), f(x)
已知函数 f(x)的导函数是 。对任意两个不相等的正数
x
x、x ，证明：
1 2
f(x ) f(x ) x x
（Ⅰ）当a0时， 1 2  f( 1 2)；
2 2
（Ⅱ）当a4时， f(x ) f(x )  x x 。
1 2 1 2
2006年四川高考理科数学真题参考答案
一．选择题：本大题共12小题，每小题5分，共60分；
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 C D D B D B A C A C A B
二．填空题：本大题共4小题，每小题4分，共16分；把答案填在题中的横线上。
1
（13）arctan 2 ；（14） ；（15）35；（16）①，③
10
三．解答题：本大题共6小题，共74分；解答应写出文字说明，证明过程或演算步骤。
（17）本小题主要考察三角函数概念、同角三角函数的关系、两角和与差的三角函数的公式
以及倍角公式，考察应用、分析和计算能力。满分12分。
   
解：（Ⅰ）∵mn1∴ 1, 3 cosA,sinA1即 3sin AcosA1
2  

sinA 3 cosA 1 

1,sin  A   1
 2 2   6 2
  5   
∵0 A,  A  ∴A  ∴A
6 6 6 6 6 3
12sinBcosB
（Ⅱ）由题知 3，整理得sin2 BsinBcosB2cos2 B0
cos2 Bsin2 B
∴cosB0∴tan2 BtanB20
∴tanB2或tanB1
而tanB1使cos2 Bsin2 B0，舍去∴tanB2
tan AtanB 2 3 85 3
∴tanC tanAB tanAB   
 
1tan AtanB 12 3 11
（18）（本大题满分12分）
本小题主要考察相互独立事件、互斥事件、对立事件等概率的计算方法，考察应用概率知识
解决实际问题的能力。满分12分。
解：记“甲理论考核合格”为事件A；“乙理论考核合格”为事件A ；“丙理论考核合格”
1 2
为事件A ；记A 为A的对立事件，i 1,2,3；记“甲实验考核合格”为事件B ；“乙实验
3 i i 1
第4页 | 共12页考核合格”为事件B ；“丙实验考核合格”为事件B ；
2 3
（Ⅰ）记“理论考核中至少有两人合格”为事件C，记C为C的对立事件
解法1：PC P  AA A  A A A  AA A  AA A 
1 2 3 1 2 3 1 2 3 1 2 3
 P  AA A  P  A A A  P  AA A  PAA A 
1 2 3 1 2 3 1 2 3 1 2 3
0.90.80.30.90.20.70.10.80.70.90.80.7
0.902
解法2：PC1P  C  1P  A A A  A A A  AA A  A A A 
1 2 3 1 2 3 1 2 3 1 2 3
1P  A A A  P  A A A  P  AA A  P  A A A 
 1 2 3 1 2 3 1 2 3 1 2 3 
10.10.20.30.90.20.30.10.80.30.10.20.7
10.098 0.902
所以，理论考核中至少有两人合格的概率为0.902
（Ⅱ）记“三人该课程考核都合格”为事件D
PD PA B A B A B 
 1 1 2 2 3 3 
 PA B PA B PA B 
1 1 2 2 3 3
 PA PB PA PB PA PB 
1 1 2 2 3 3
0.90.80.80.80.70.9
0.254016
0.254
所以，这三人该课程考核都合格的概率为0.254
（19）（本大题满分12分）
本小题主要考察长方体的概念、直线和平面、平面和平面的关系等基础知识，以及空间想象
能力和推理能力。满分12分
解法一：（Ⅰ）证明：取CD的中点K，连结MK,NK
∵M,N,K 分别为AK,CD,CD的中点
1
∵MK // AD,NK //DD
1
∴MK //面ADD A ，NK //面ADD A
1 1 1 1
∴面MNK //面ADD A ∴MN //面ADD A
1 1 1 1
（Ⅱ）设F 为AD的中点
∵P为AD 的中点∴PF//DD∴PF 面ABCD
1 1 1
第5页 | 共12页作FH  AE，交AE于H ，连结PH ，则由三垂线定理得AE  PH
从而PHF为二面角PAED的平面角。
a
a 17 2a
在RtAEF 中，AF  ,EF 2a,AE  a，从而 AFEF 2 2a
FH   
2 2
AE 17 17
a
2
PF DD 17
在RtPFH 中，tanPFH   1 
FH FH 2
17
故：二面角PAED的大小为arctan
2
1 1 1 5
（Ⅲ）S  S  BCCD  a a2 4a2  a2
NEP 2 矩形ECD 1 P 4 1 4 4
作DQCD ，交CD 于Q，由AD 面CDDC 得AC  DQ
1 1 1 1 1 1 1 1
∴DQ面BCD A
1 1
CDDD 2aa 2
∴在RtCDD 中，DQ 1   a
1 CD 5a 5
1
1 1 5 2 1
∴V V  S DQ  a2 a  a3
PDEN DENP 3 NEP 3 4 5 6
方法二：以D为原点，DA,DC,DD 所在直线分别为x轴，y轴，z轴，建立直角坐标系，
1
则
Aa,0,0,Ba,2a,0,C0,2a,0,A a,0,a,D 0,0,a
1 1
∵E,P,M,N分别是BC,AD,AE,CD 的中点
1 1 1
a  a  3a   a
∴E ,2a,0 ,P ,0,a ,M ,a,0 ,N 0,a, ,
       
2  2   4   2
  3 a
（Ⅰ）MN 

 a,0,

 4 2
 
取n0,1,0，显然n面ADD A
1 1
   
MNn0，∴MN n
又MN 面ADD A ∴MN //面ADD A
1 1 1 1
a 
（Ⅱ）过P作PH  AE，交AE于H ，取AD的中点F ，则F  ,0,0 ∵
2 
第6页 | 共12页设Hx,y,0，则 
H

P




a
x,y,a

,

H

F




a
x,y,0


2  2 
  a 
又AE   ,2a,0
 
 2 
 a2 a
 
由APAE 0，及H 在直线AE上，可得:
  x2ay0
 4 2

 4x y4a
33 2
解得x a,y  a
34 17
  8a 2a    8a 2a     
∴HP , ,a  ,HF  , ,0  ∴HFAE 0即HF  AE
 17 17   17 17 
 
∴HP与HF所夹的角等于二面角PAED的大小
 
  HPHF 2
cos HP,HF  
 
HP  HF 21
2 21
故：二面角PAED的大小为arccos
21
    
（Ⅲ）设n x ,y ,z 为平面DEN的法向量，则n  DE,n  DN
1 1 1 1 1 1
 a    a  a 
又DE  ,2a,0 ,DN  0,a, ,DP ,0,a
     
2   2 2 
a
x 2ay 0
 2 1 1 x 4y 
∴ 即 1 1∴可取n 4,1,2
a z 2y 1
 2y  z 0  1 1
 1 2 1
 
DPn 2a2a 4a
1
∴P点到平面DEN的距离为d   

n 1614 21
1
 
  DEDN 8   21
∵cos DE,DN   ，sin DE,DN 
 
DE  DN 85 85
1     21
∴S  DE  DN sin DE,DN  a2
DEN 2 8
1 1 21 4a a3
∴V  S d   a2 
PDEN 3 DEN 3 8 21 6
（20）（本大题满分12分）
第7页 | 共12页本小题主要考察等差数列、等比数列的基础知识，以及对数运算、导数运算和极限运算的能
力，同时考查分类讨论的思想方法，满分12分。
解：（Ⅰ）由题意，a 是首项为1，公差为2的等差数列
n
112n1
前n项和S  nn2，lnS lnn2 2lnn
n 2 n
U 2ln1ln2 lnn2lnn!
n 
（Ⅱ）F x eUn x2n  n!2 x2n  x2n F 'x x2n1
n 2nn!2 2nn!2 2n n
x  1x2n
 0x1
 1x2
n n 
T xF'xx2k1 n x1
n k
k1 k1 
x
 1x2n
 x1
  1x2




1x2n
lim 1 0 x1
 n1x2n2

T x  n
lim n lim 1 x1
nT
n1
x nn1
  1 
1
  
 x2n 
lim x1
n 1 
x2
    x2n  
（21）（本大题满分14分）
本小题主要考察双曲线的定义和性质、直线与双曲线的关系、点到直线的距离等知识及解析
几何的基本思想、方法和综合解决问题的能力。满分12分。
解：由双曲线的定义可知，曲线E是以F   2,0  ,F  2,0  为焦点的双曲线的左支，
1 2
且c 2,a1，易知b1
故曲线E的方程为x2  y2 1x0
 y kx1
设Ax ,y ,Bx ,y ，由题意建立方程组
1 1 2 2 x2  y2 1
消去 y，得  1k2 x2 2kx20
又已知直线与双曲线左支交于两点A,B，有
第8页 | 共12页 1k2 0

2k2 8  1k2 0

解得 2 k 1
2k

x x  0
 1 2 1k2

2
 xx  0
 1 2 1k2
又∵ AB  1k2  x x  1k2  x x 2 4x x
1 2 1 2 1 2
 2k  2 2
 1k2 2k2
 1k2    4 2
1k2  1k2  1k22
 1k2 2k2
依题意得 整理后得28k4 55k2 250
2 6 3
 1k22
5 5 5
∴k2  或k2  但 2 k 1∴k 
7 4 2
5
故直线AB的方程为 x y10
2
  
设Cx ,y ，由已知OAOBmOC，得x ,y x ,y mx ,my 
c c 1 1 2 2 c c
 x x y  y 
∴mx ,my  1 2 , 1 2 ，m0
 
c c  m m 
2k 2k2 2
又x x  4 5，y  y kx x 2 2 8
1 2 k2 1 1 2 1 2 k2 1 k2 1
4 5 8 
∴点
C , 
 
m m
 
80 64
将点C的坐标代入曲线E的方程，得  1
m2 m2
得m4，但当m4时，所得的点在双曲线的右支上，不合题意
 
∴m4，C点的坐标为  5,2
5  
C到AB的距离为   5 21
2 1

2 3
 5
  12
2
 
1 1
∴ABC的面积S  6 3  3
2 3
（22）（本大题满分14分）
第9页 | 共12页本小题主要考查导数的基本性质和应用，函数的性质和平均值不等式等知识及综合分析、推
理论证的能力，满分14分。
2
证明：（Ⅰ）由 f x x2  alnx
x
f x  f x  1  1 1  a
得 1 2   x2 x 2    lnx lnx 
2 2 1 2 x x  2 1 2
1 2
1 x x
  x2 x 2  1 2 aln x x
2 1 2 x x 1 2
1 2
2
x x  x x  4 x x
f 1 2  1 2  aln 1 2
   
 2   2  x x 2
1 2
而 1 2  x 1 2x 2 2  1 4    x 1 2x 2 2 2x 1 x 2   2     x 1  2 x 2    2 ①
又x x 2   x2 x 2 2x x 4x x
1 2 1 2 1 2 1 2
x x 4
∴ 1 2  ②
x x x x
1 2 1 2
x x x x
∵ x x  1 2 ∴ln x x ln 1 2
1 2 2 1 2 2
x x
∵a0∴aln xx aln 1 2 ③
1 2 2
由①、②、③得
2
1  x2x 2  x 1 x 2 aln xx  x 1 x 2   4 aln xx
 
2 1 2 xx 1 2  2  x x 1 2
1 2 1 2
f x  f x  x x 
即 1 2  f 1 2
 
2  2 
2 2 a
（Ⅱ）证法一：由 f x x2  alnx，得 f'x2x 
x x2 x
 2 a   2 a  2x x  a
∴ f'x  f'x   2x   2x     x x  2 1 2 
1 2  1 x2 x   2 x 2 x  1 2 x2x 2 xx
1 1 2 2 1 2 1 2
2x x  a
f'x  f'x   x x  2 1 2  1
1 2 1 2 x2x 2 x x
1 2 1 2
2x x  a
下面证明对任意两个不相等的正数x ,x ,有2 1 2  1恒成立
1 2 x2x 2 x x
1 2 1 2
第10页 | 共12页2x x 
即证a x x  1 2 成立
1 2 x x
1 2
2x x  4
∵x x  1 2  x x 
1 2 x x 1 2 x x
1 2 1 2
4 4
设t  x x ,uxt2  t 0，则u'x2t
1 2 t t2
令u'x0得t  3 2 ，列表如下：
   
t 0,3 2 3 2 3 2,
u't _ 0 
ut
极小值33 4
 
2x x 
ut33 4  3108 4a∴x x  1 2 a
1 2 x x
1 2
∴对任意两个不相等的正数x ,x ，恒有 f 'x  f 'x   x x
1 2 1 2 1 2
2 2 a
证法二：由 f x x2  alnx，得 f 'x2x 
x x2 x
2x x  a
∴ f'x 1  f'x 2      2x 1  x 2 1 2  x a 1        2x 2  x 2 2 2  x a 2     x 1 x 2  2 x 1 1 2x 2 2 2  x 1 x 2
∵x ,x 是两个不相等的正数
1 2
2x x  a 4 a 4 4
∴2 1 2  2  2 
x2x 2 xx  3 xx  3 x x
1 2 1 2 xx 1 2 x x 1 2
1 2 1 2
1
设t  ，ut24t34t2t 0
x x
1 2
则u't4t3t2，列表：
 2 2 2 
t  0,   , 
 3 3 3 
u't _ 0 
38
ut 极小值
 
27
第11页 | 共12页38 2x x  a
∴u  1即2 1 2  1
27 x2x 2 x x
1 2 1 2
2x x  a
∴ f'x  f'x   x x  2 1 2   x x
1 2 1 2 x2x 2 x x 1 2
1 2 1 2
即对任意两个不相等的正数x ,x ，恒有 f 'x  f 'x   x x
1 2 1 2 1 2
第12页 | 共12页