数学答案_2024-2025高三（6-6月题库）_2026年1月高三_260131山东省济南市2025-2026年高三上第一次模拟考试（全科）_山东省济南市2025-2026年高三上第一次模拟考试数学

济南市 2026 届高三第一次模拟考试 数学试题参考答案 一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只 有一项是符合题目要求的． 题号 1 2 3 4 5 6 7 8 答案 A B C B B D D C 二、多项选择题：本题共3小题，每小题6分，共18分．在每小题给出的四个选项中，有 多项符合题目要求．全部选对的得6分，部分选对的得部分分，有选错的得0分． 题号 9 10 11 答案 BC ABD BCD 三、填空题：本题共3小题，每小题5分，共15分． 12． 数学试题答案 第1页 5 ； 13． 0 ； 14．9． 四、解答题：共77分．解答应写出文字说明、证明过程或演算步骤． 15．【解析】 （1）当 n = 1 时，S =2a −2，a =2， 1 1 1 当n≥2时， S n = 2 a n − 2 ， S n − 1 = 2 a n − 1 − 2 ，作差得： a n = 2 a n − 2 a n − 1 ， 即 a n = 2 a n − 1 ， a a n n − 1 = 2 ， 所以  a n  是首项为2，公比为2的等比数列，所以 a n = 2 n ． （2） b n = lo g 2 a n = lo g 2 2 n = n ， T n = n ( 1 + 2 n ) ， 1 2 1 1  所以 = =2 −  ， T n(1+n) n n+1 n 所以 n i= 1 1 T i = 2   1 − 1 2  +  1 2 − 1 3  + +  1 n − n 1 + 1   = 2  1 − n 1 + 1   2 ， 命题得证． 16．【解析】 （1）取 A C 中点D，连接 A 1 D ， D N ． 因为 D ， N 为AC，BC中点， 所以 D N 为 △ A B C 的中位线， 所以 D N = 1 2 A B 且 D N A B ∥ ． 在正方形 A B B 1 A 1 中， M 为AB 中点， 1 1 1 所以AM∥AB且AM = AB， 1 1 2 所以AM∥DN 且AM =DN， 1 1 所以四边形DNMA是平行四边形． 1 所以AD∥MN ． 1又 数学试题答案 第2页 M N  平面ACA ， 1 A 1 D  平面 A C A 1 ， 所以 M N ∥平面 A C A 1 ． （2）由于平面 A B B 1 A ⊥ 平面ABC，平面 A B B 1 A 平面 A B C = A B ， A A 1 ⊥ A B ， A A 1  平面 A B B 1 A 1 ， A A 1 ⊥ 平面 A B C ． 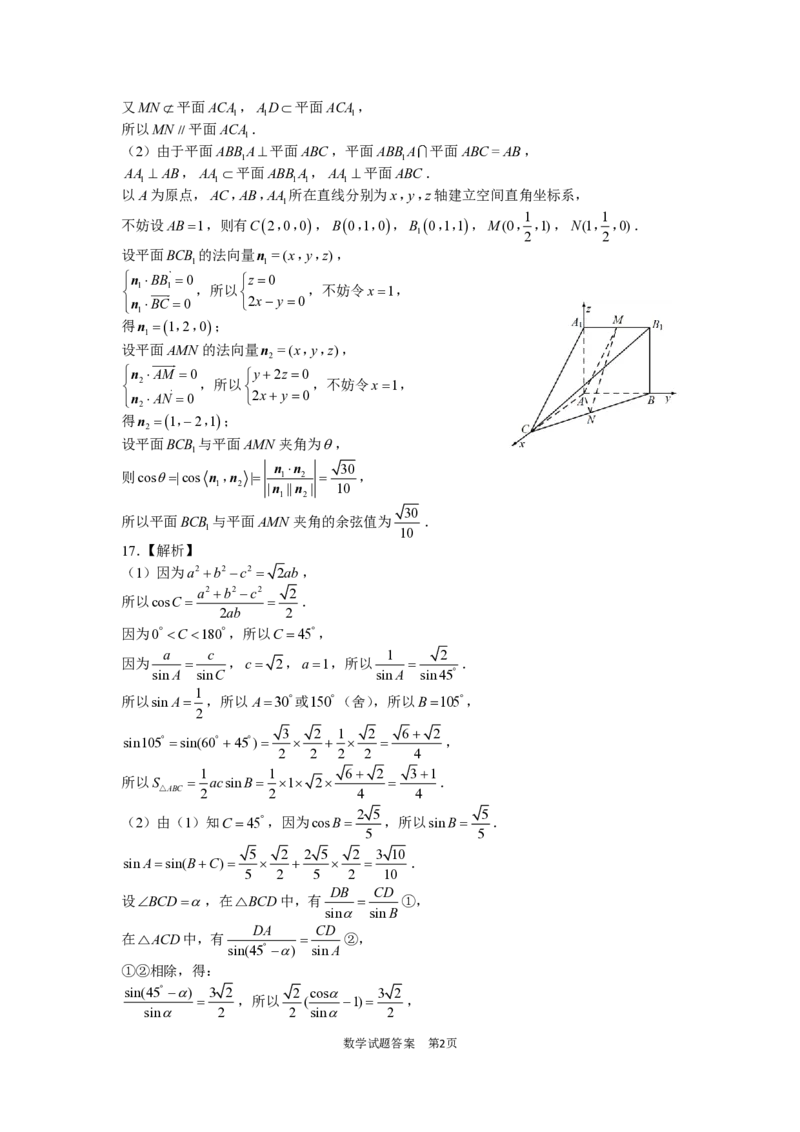以A为原点， A C ， A B ， A A 1 所在直线分别为 x ， y ， z 轴建立空间直角坐标系， 不妨设AB=1，则有 C ( 2 ， 0 ， 0 ) ， B ( 0 ， 1 ， 0 ) ， B 1 ( 0 ， 1 ， 1 ) 1 1 ，M(0， ，1)，N(1， ，0)． 2 2 设平面 B C B 1 的法向量 n 1 = ( x ， y ， z ) ，  n BB =0  1 1 ，所以 n BC =0 1  z 2 = x 0 − y = 0 ，不妨令 x = 1 ， 得 n 1 = ( 1 ， 2 ， 0 ) ； 设平面 A M N 的法向量n =(x，y，z)， 2  n n 2 2   A A M N = = 0 0 ，所以  y 2 + x + 2 z y = = 0 0 ，不妨令x=1， 得n =(1，−2，1)； 2 设平面 B C B 1 与平面 A M N 夹角为， 则 c o s | c o s 1 2 | | 1 1 || 2 2 | 1 3 0 0  = n ， n = n n  n n = ， 所以平面BCB 与平面 1 A M N 夹角的余弦值为 1 3 0 0 ． 17．【解析】 （1）因为a2 +b2 −c2 = 2ab， 所以 c o s C = a 2 + 2 b a 2 b − c 2 = 2 2 ． 因为 0   C  1 8 0  ，所以 C = 4 5  ， 因为 s a in A = s c in C ， c = 2 ， a = 1 ，所以 s 1 in A = s in 2 4 5  ． 所以 s in A = 1 2 ，所以A=30或150（舍），所以B=105， s in 1 0 5  = s in ( 6 0  + 4 5  ) = 2 3  2 2 + 1 2  2 2 = 6 + 4 2 ， 所以 S △ A B C = 1 2 a c s in B = 1 2  1  2  6 + 4 2 = 3 4 + 1 ． （2）由（1）知 C = 4 5  ，因为 c o s B = 2 5 5 ，所以 s in B = 5 5 ． 5 2 2 5 2 3 10 sinA=sin(B+C)=  +  = ． 5 2 5 2 10 设BCD=，在△BCD中，有 s D in B s C in D B  = ①， DA CD 在△ACD中，有 = ②， sin(45 −) sinA ①②相除，得： sin(45 −) 3 2 2 cos 3 2 = ，所以 ( −1)= ， sin 2 2 sin 2所以 数学试题答案 第3页 c s o s in 4   = ，即 ta n 1 4  = ， 所以  B C D 的正切值为 1 4 ． 18．【解析】  2a=4  （1）由题意可知 9 25 ， − =1  a2 4b2 解得 a = 2 ， b = 5 ， 故C的方程为 x 4 2 − y 5 2 = 1 ． （2）（i）因为A(2,0)， P ( 3 , 5 2 ) ，所以直线 A P 方程为 y = 5 2 x − 5 ， 由于 M ( x 1 , y 1 ) ，故 R ( x 1 , 5 2 x 1 − 5 ) ， 因为 M R = R S ，所以S(x,5x −10−y )， 1 1 1 所以 k 0 = 5 x 1 − x 1 1 0 − − 2 y 1 = 5 − x 1 y 1− 2 ． （ii）由（i）可知 k A N + k A M = k A S + k A M = 5 − x 1 y 1− 2 + x 1 y 1− 2 = 5 ， y y 即 1 + 2 =5． x −2 x −2 1 2 由题意可知，直线 M N 的斜率显然存在， 设直线 M N : y = k x + m x2 y2  − =1 ，联立 4 5 ，消   y=kx+m y 得 ( 5 − 4 k 2 ) x 2 − 8 k m x − 4 m 2 − 2 0 = 0 ， x 1 + x 2 = 5 8 − k m 4 k 2 ， x 1 x 2 = − 4 m 5 2 − + 4 k 2 2 0 ，0， x 1 y 1− 2 + x 2 y 2− 2 = k x x 1 1 + − m 2 + k x x 2 2 + − m 2 = 2 k x 1 x 2x + 1 x ( 2 m − − 2 2 k ( x 1 ) ( + x 1x 2 + ) x + ) 24 − 4 m = m 5 + 2 k = 5 ， 所以 m = 1 − 2 k ， 所以直线 M N : y = k x + 1 − 2 k = k ( x − 2 ) + 1 ， 所以直线 M N 过定点 ( 2 ， 1 ) ． 19．【解析】 sinx （1）令 f '(x)= =0，得 x x = n π ，nN*， 因为x=nπ为 f(x)的变号零点，所以x =n． n 当x(x ,x )时，2x −x0，且 n n+1 n+1 s i n x  0 ． sin(2(n+1)π−x) sin(2(n+1)π−x) |sinx| |sinx| | f '(2x −x)|= = = ，| f(x)|= ， n+1 2x −x |2x −x| 2x −x x n+1 n+1 n+1 | f '( x ) | − | f '( 2 x n + 1 − x ) |= | s in x x | − 2 | s in x n + 1 x − | x = | s in x |  2 ( x ( 2 x n + 1 x n + 1 − − x ) x )  0 ． 故| f(x)|| f(2x −x)|． n+1（2）选择①， 令g(x)= f(x)− f(2x −x)， 2n 数学试题答案 第4页 x  [ x 2 n − 1 , x 2 n ] ， 则 g '( x ) = f '( x ) + f '( 2 x 2 n − x ) ， 当 x  [ x 2 n − 1 , x 2 n ] 时，即 x  [ ( 2 n − 1 ) π , 2 n π ] 时， 2 x 2 n − x  [ 2 n π , ( 2 n + 1 ) π ] ， f ( x ) = s in x x ≤ 0 ， f '( 2 x 2 n − x ) = − 2 s x in 2 n x − x ≥ 0 ， 故 g '( x ) = f '( x ) + f '( 2 x 2 n − x ) = − | f '( x ) | + | f '( 2 x 2 n − x ) | ， 由（1）知， g ( x ) ≤ 0 ． 故 g ( x ) 单调递减，从而有 g ( x 2 n − 1 )  g ( x 2 n ) = f ( x 2 n ) − f ( 2 x 2 n − x 2 n ) = 0 ， 即g(x )= f(x )− f(2x −x )= f(x )− f(x )0， 2n−1 2n−1 2n 2n−1 2n−1 2n+1 即 f ( x 2 n − 1 )  f ( x 2 n + 1 ) ，从而数列 { f ( x 2 n − 1 ) } 为递减数列． 选择②， 令 g ( x ) = f ( x ) − f ( 2 x 2 n + 1 − x ) ， x  [ x 2 n , x 2 n + 1 ] ， 则 g '( x ) = f '( x ) + f '( 2 x 2 n + 1 − x ) ， 当 x  [ x 2 n , x 2 n + 1 ] 时，即 x  [ 2 n π , ( 2 n + 1 ) π ] 时， 2 x 2 n + 1 − x  [ ( 2 n + 1 ) π , ( 2 n + 2 ) π ] ， f ( x ) = s in x x ≥ 0 sinx ， f '(2x −x)=− ≤0， 2n+1 2x −x 2n+1 故g'(x)= f '(x)+ f '(2x −x)=| f '(x)|−| f '(2x −x)| ， 2n+1 2n+1 由（1）知， g '( x ) ≥ 0 ， 故 g ( x ) 单调递增，从而有g(x )g(x )= f(x )− f(2x −x )=0， 2n 2n+1 2n+1 2n+1 2n+1 即 g ( x 2 n ) = f ( x 2 n ) − f ( 2 x 2 n + 1 − x 2 n ) = f ( x 2 n ) − f ( x 2 n + 2 )  0 ， 即 f(x ) f(x )，从而数列 2n 2n+2 { f ( x 2 n ) } 为递增数列． （3）由（2）知， f ( x ) 的最大值为 f ( x 1 ) = f ( π ) ， f ( x ) 的最小值为 f(x )= f(2π)， 2 对任意 x 1 , x 2  [ π , +  ) ，都有 | f ( x 1 ) − f ( x 2 ) |≤ k 成立， 当且仅当 f ( π ) − f ( 2 π ) ≤ k ． 当k =1时，令 h ( x ) = f ( x ) + x π ， x  [ π , 2 π ] ， sinx 1 则h'(x)= + ， x π 注意到 − 1 ≤ s in x ≤ 0 ，且π≤x≤2π， 从而有 h '( x ) ≥ s in x x + 1 π ≥ s in π x + 1 π ≥ 0 ， 故 h ( x ) 单调递增． 故h(π)h(2π)，即 f(π)+1 f(2π)+2，故 f(π)− f(2π)1． 从而k的最小值为1．