文档内容
2024-2025学年高二下学期3月联考数学试题
一、单选题
1. ,则 ( )
A. B.2 C. D.6
2.拉格朗日中值定理又称拉氏定理:如果函数 在 上连续,且在 上可导,则必有 ,
使得 .已知函数 ,那么实数 的最大
值为( )
A.1 B. C. D.0
3.对于函数 ,部分x与y的对应关系如下表:
x 1 2 3 4 5 6 7 8 9
y 3 7 5 9 6 1 8 2 4
数列 满足: ,且对于任意 ,点 都在函数 的图象上,则
( )
A.7569 B.7576 C.7584 D.7590
4.南宋数学家杨辉在《详解九章算法》和《算法通变本末》书中提出高阶等差数列前后两项之差不相等,
但是逐项差数之差或者高次差成等差数列.现有高阶等差数列,其前6项分别是1,6,13,24,41,66,则
该数列的第7项为( )
A.91 B.99 C.101 D.113
5.在等比数列 中, , 是方程 的两个根,则 ( )
A. B.2 C.1 D.
6.已知 , ,则a,b的等差中项为( )A. B. C.1 D.
7.数列 , , ,…, ,…的第10项是( )
A. B. C. D.
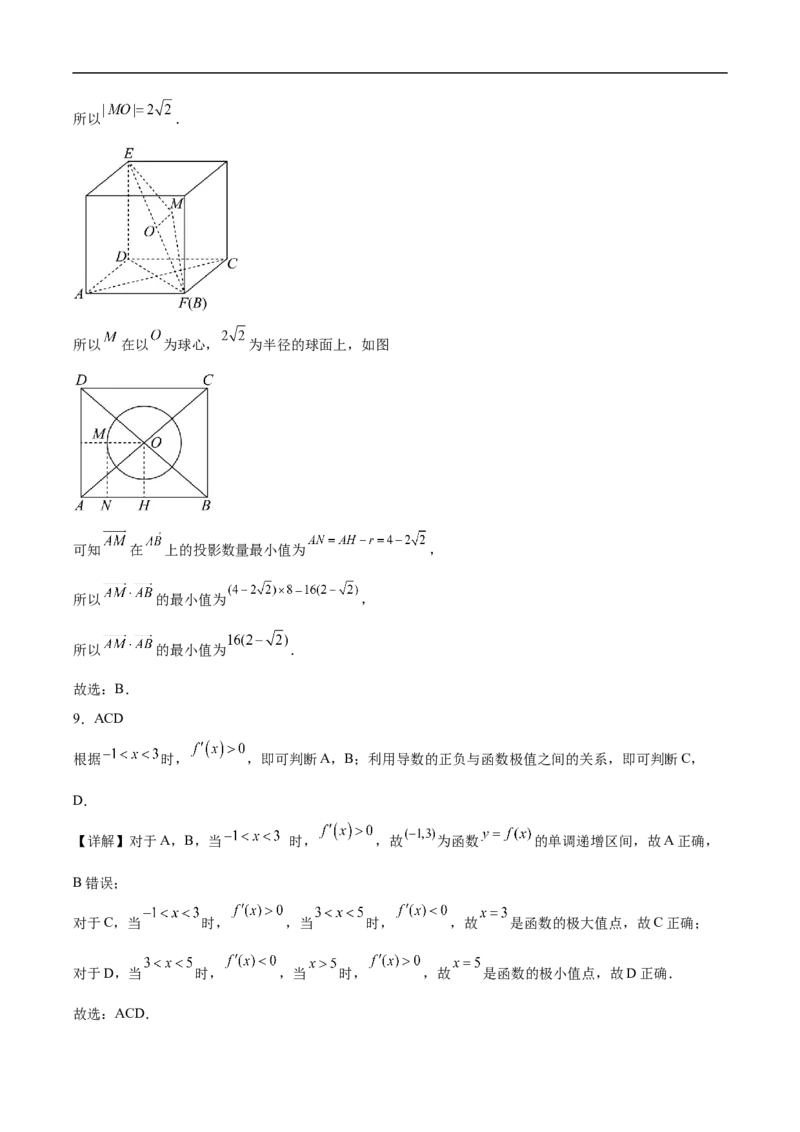
8.已知EF是棱长为8的正方体的一条体对角线,空间一点M满足 ,AB是正方体的一条棱,
则 的最小值为( )
A. B. C. D.
二、多选题
9.如图是导函数 的图象,则下列说法正确的是( )
A. 为函数 的单调递增区间
B. 为函数 的单调递减区间
C.函数 在 处取得极大值
D.函数 在 处取得极小值
10.甲、乙、丙、丁四名志愿者到A,B,C三所山区学校参加支教活动,每个志愿者仅在一所学校支教,
要求每所学校至少安排一名志愿者,则下列结论中正确的是( )
A.共有72种安排方法
B.若甲被安排在A学校,则有12种安排方法
C.若A学校需要两名志愿者,则有12种安排方法
D.若甲、乙不能在同一所学校,则有30种安排方法
11.已知等差数列 的前 项和为 ,若 ,则( )A.公差 B.
C. 的最大值为 D.满足 的 的最小值为16
三、填空题
12.已知 ,那么 ;
13.已知函数 是 上的减函数,则实数 的取值范围是 .
14.设点 在抛物线 上,已知 .若 ,则 ;若 ,
则直线 斜率的最小值为 .
15.已知圆系 ,圆 过 轴上的定点 ,线段 是圆 在 轴上截得
的弦,设 , .对于下列命题:
①不论 取何实数,圆心 始终落在曲线 上;
②不论 取何实数,弦 的长为定值1;
③不论 取何实数,圆系 的所有圆都与直线 相切;
④式子 的取值范围是 .
其中真命题的序号是 (把所有真命题的序号都填上)
四、解答题
16.盒子内有3个不同的黑球,5个不同的白球.
(1)全部取出排成一列,3个黑球两两不相邻的排法有多少种?
(2)从中任取6个球,白球的个数不比黑球个数少的取法有多少种?
(3)若取一个白球记2分,取一个黑球记1分,从中任取5个球,使总分不少于7分的取法有多少种?
17.“每天锻炼一小时,健康工作五十年,幸福生活一辈子.”一科研单位为了解员工爱好运动是否与性
别有关,从单位随机抽取30名员工进行了问卷调查,得到了如下列联表:男性 女性 合计
爱好 10
不爱好 8
合计 30
已知在这30人中随机抽取1人抽到爱好运动的员工的概率是 .
参考公式: .
附表:
0.100 0.050 0.010 0.005 0.001
2.706 3.841 6.635 7.879 10.828
(1)请将上面的列联表补充完整,根据小概率值 的独立性检验,分析爱好运动与否与性别是否有关?
(2)若从这 人中的女性员工中随机抽取 人参加一活动,记爱好运动的人数为 ,求 的分布列、数学
期望.
18.已知数列 满足 .
(1)求 的通项公式;
(2)已知 ,求数列 的前20项和.
19.对于正实数 有基本不等式: ,其中 ,为 的算术平均数,
,为 的几何平均数.现定义 的对数平均数:
(1)设 ,求证: :
(2)①证明不等式: :
②若不等式 对于任意的正实数 恒成立,求正实数 的最大值.题号 1 2 3 4 5 6 7 8 9 10
答案 C C D C A B A B ACD BCD
题号 11
答案 AC
1.C
根据导数的定义,结合导数的计算,可得答案.
【详解】∵ , ,∴ .
故选:C.
2.C
利用导数判断单调性,求解出值
【详解】因为函数 在 上连续,且在 上可导,则必有一 ,使得 ,
又函数 ,可得 ,
所以 ,此时 ,
又 ,所以 ,因为 ,且 ,所以 ,
不妨设 ,函数定义域为 ,可得 ,
当 时, , 单调递增;
当 时, , 单调递减,
所以当 时,函数 取得极大值也是最大值,最大值 ,
则当 时,λ取得最大值,最大值为 .
故选:C.
3.D
根据题意得到数列 是周期为 的周期数列,然后求和即可.
【详解】由题意,数列 满足 ,且点 都在函数 的图象上,可得 ,
,
,
,
则数列 是周期为 的周期数列,
即数列 满足 ,
则 .
故选:D.
4.C
根据高阶等差数列的定义,逐项作差,可推得 为等差数列,且 ,反向求解可得 ,
.
【详解】由已知可设 , , , , , .
设 ,则 , , , , .
设 ,则 , , , ,
根据高阶等差数列的定义以及 的前4项可知, 为等差数列,所以 ,即 ,
所以 ,即 ,
所以 .
故选:C.
5.A
利用根与系数的关系和等比数列的性质求解即可【详解】由题意可得
所以 .
因为
所以 , ,所以 ,
所以 ,所以 .
故选:A.
6.B
先求解可得 ,然后根据等差中项的性质,即可得出答案.
【详解】由已知可得, .
设a,b的等差中项为 ,
根据等差中项的定义,有 .
故选:B.
7.A
由观察可得数列规律,即可得答案.
【详解】由题可得数列第n项为 ,则数列第10项为 .
故选:A
8.B
由空间向量的数量积运算计算可得 ,即可得 的轨迹,即可根据数量积的几何意义求解即可.
【详解】取 的中点 , ,
则 ,所以 .
所以 在以 为球心, 为半径的球面上,如图
可知 在 上的投影数量最小值为 ,
所以 的最小值为 ,
所以 的最小值为 .
故选:B.
9.ACD
根据 时, ,即可判断A,B;利用导数的正负与函数极值之间的关系,即可判断C,
D.
【详解】对于A,B,当 时, ,故 为函数 的单调递增区间,故A正确,
B错误;
对于C,当 时, ,当 时, ,故 是函数的极大值点,故C正确;
对于D,当 时, ,当 时, ,故 是函数的极小值点,故D正确.
故选:ACD.10.BCD
由分类加法计数原理,结合分步乘法计数原理以及分组分配问题,结合间接法即可求解.
【详解】对于A,共有 种安排方法,即A错误;
对于B,若甲被安排在 学校,则有 种安排方法,即B正确;
对于C,若 学校需要两名志愿者,则有 种安排方法,即C正确;
对于D,若甲、乙不能在同一所学校,则有 种安排方法,即D正确.
故选:BCD.
11.AC
根据 求出 与公差 的关系即可判断AB;再根据等差数列前 项和公式即可判断CD.
【详解】因为 ,
则 ,即 ,
则 ,故A正确;
,故B错误;
由 ,得 ,
,
因为 ,
所以数列 是递减数列,且当 时, ,当 时, ,
所以 的最大值为 ,故C正确;
,
令 ,解得 ,所以满足 的 的最小值为 ,故D错误.
故选:AC.
12.
根据组合数的性质及组合数的计算公式计算可得;
【详解】解:因为 ,所以 ,即 ,即 ,解得 或 (舍
去)
故答案为:
13.
由函数 是 上的减函数,列出相应的不等式组,即可求解实数 的取值范围.
【详解】∵函数 是 上的减函数,
∴ ,解得 .
∴实数 的取值范围是 .
答案: .
14. 3 1
第一空:由两点间距离公式以及点 坐标满足抛物线方程联立列式即可求解;第二空:将直线 斜率表
达式求出来,结合基本不等式即可得解.
【详解】第一空:若 ,则 ,
又 ,所以 ,注意到 ,
所以解得 满足题意;第二空:直线 斜率为 ,若 ,
则由基本不等式得 ,等号成立当且仅当 .
故答案为:3;1.
15.②④
对于①,根据圆 的方程即可判断①,对于②,根据弦长公式即可判断②,根据圆心 到直线 的
距离即可判断③,对于④,令 求出点 和点 的坐标,根据圆 方程求出点 坐标,求出 和
,在 利用余弦定理求出 ,求出 的面积即可求出 ,根据 即可判断
④.
【详解】对于①,由圆 的方程知,圆心 在曲线 上,故①不正确.
对于②,由弦长公式得:弦 的长为 ,故②正确.
对于③,圆心 到直线 的距离等于 ,
而半径为 ,二者不一定相等,故③不正确.
对于④,在圆 方程令 ,可得 ,
或 ,即 , , , ,
由圆 方程知 , , ,
由基本不等式得 (当且仅当 ,即 时等号成立),
中,由余弦定理得 ,
, 的面积为 ,
, ,,即 ,故④正确.
故答案为: ②④.
16.(1)14400; (2)28; (3)56.
【解析】(1)首先5个白球进行排列,然后3个黑球进行插空,则3个黑球两两不相邻的排法有 ;
(2)从中任取6个球,白球的个数不比黑球个数少的取法有3类:1个黑球和5个白球、2个黑球和4个
白球、3个黑球和3个白球;(3)从中任取5个球,使总分不少于7分的取法有4类:5个白球、4个白球
1个黑球、3个白球2个黑球、2个白球3个黑球.
【详解】(1)首先5个白球进行排列,然后3个黑球进行插空,则3个黑球两两不相邻的排法有
种;
(2)从中任取6个球,白球的个数不比黑球个数少的取法有3类:1个黑球和5个白球、2个黑球和4个
白球、3个黑球和3个白球,共有 种;
(3)从中任取5个球,使总分不少于7分的取法有4类:5个白球、4个白球1个黑球、3个白球2个黑球、
2个白球3个黑球,共有 种.
17.(1)列联表见解析,认为爱好运动与否与性别没有关系
(2)分布列见解析,
(1)先完善列联表,根据题干附注公式计算 ,对比附注表格的临界值,然后得出结论;
(2) 人中,女性 人,按照步骤写出分布列中的每一条概率值,然后得到期望.
【详解】(1)由30人中随机抽取1人抽到爱好运动的员工的概率是 ,故爱好运动的员工共有16人,
由表中男爱好运动的员工为10人,可得女爱好运动的员工有6人,
故列联表补充如下:
男性 女性 合计
爱好 10 6 16
不爱好 6 8 14
合计 16 14 30零假设为 :爱好运动与否与性别没有关系.
由已知数据可求得:
,
根据小概率值 的独立性检验,没有充分证据推断 不成立,即接受 ,即认为爱好运动与否与
性别没有关系;
(2) 的可能取值为 ,由于女性有 人,爱好活动的 人,
,
,
所以 的分布列为:
0 1 2
的数学期望为:
.
18.(1)
(2)5
【详解】(1)当 时,可得 ,
当 时, ,
,
上述两式作差可得 ,因为 满足 ,所以 的通项公式为 .
(2)因为 ,
所以 ,
.
+ =5
所以数列 的前20项和为5.
19.(1)证明见解析
(2)①证明见解析;②2
【详解】(1)令 ,则 ,
,得 在 , 上单调递减,
又 (1) ,故当 时, ,
因此,当 时, ;
(2)(2)①证明:要证 , , ,只要证 ,
只要证 ,即证 ,
令 ,由(1)有 ,即得 ,
因此, ;
②由 , , , 恒成立,得 恒成立,即得 恒成立,
令 ,有 恒成立,
得 恒成立, 恒成立,
令 ,有 ,
又 (1) ,
当 (1) ,即 时,
方程 有一根 大于1,一根 小于1,
可得 在 , 上单调递增,故有 (1) ,不符合;
当 时,有 ,
,从而 在 , 上单调递减,
故当 时,恒有 (1) ,符合.
综上所述,正实数 的取值范围为 ,